Régression linéaire multiple dans R : Tutoriel avec exemples

Les méthodes de régression sont utilisées dans différents secteurs pour comprendre quelles variables ont un impact sur un sujet donné. 

Par exemple, les économistes peuvent les utiliser pour analyser la relation entre les dépenses de consommation et la croissance du produit intérieur brut (PIB). Les responsables de la santé publique pourraient vouloir comprendre les coûts des individus sur la base de leurs informations historiques. Dans les deux cas, il ne s'agit pas de prévoir des scénarios individuels, mais d'obtenir une vue d'ensemble de la relation globale.

Dans cet article, nous commencerons par donner une compréhension générale des régressions. Ensuite, nous expliquerons ce qui différencie les régressions linéaires simples et multiples avant de nous plonger dans les implémentations techniques et de fournir des outils pour vous aider à comprendre et à interpréter les résultats de la régression.

Qu'est-ce que la régression linéaire multiple ?

Comprenons d'abord ce qu'est une régression linéaire simple avant de nous intéresser à la régression linéaire multiple, qui n'est qu'une extension de la régression linéaire simple.

Régression linéaire simple

Une régression linéaire simple vise à modéliser la relation entre l'ampleur d'une variable indépendante unique X et une variable dépendante Y en essayant d'estimer exactement de combien Y changera lorsque X changera d'un certain montant. 

• La variable indépendante X, également appelée prédicteur, est la variable utilisée pour faire la prédiction. 
• La variable dépendante Y, également appelée réponse, est celle que nous essayons de prédire.

L'aspect "linéaire" de la régression linéaire est que nous essayons de prédire Y à partir de X à l'aide de l'équation "linéaire" suivante. 

Y = b0 + b1X 

• b0 est l'ordonnée à l'origine de la droite de régression, correspondant à la valeur prédite lorsque X est nul. 
• b1 est la pente de la ligne de régression.

Qu'en est-il de la régression linéaire multiple ?

Il s'agit de l'utilisation de la régression linéaire avec des variables multiples, et l'équation est la suivante :

Y = b0 + b1X1 + b2X2 + b3X3 + … + bnXn + e

• Y et b0 sont les mêmes que dans le modèle de régression linéaire simple. 
• b1X1 représente le coefficient de régression (b1) sur la première variable indépendante (X1). La même analyse s'applique à tous les autres coefficients et variables de régression. 
• e est l'erreur du modèle (résidus), qui définit l'ampleur de la variation introduite dans le modèle lors de l'estimation de Y.

Il se peut que nous n'obtenions pas toujours une ligne droite dans le cas d'une régression multiple. Cependant, nous pouvons contrôler la forme de la ligne en appliquant un modèle plus approprié. 

Ce sont quelques-uns des éléments clés calculés par la régression linéaire multiple pour trouver la meilleure ligne d'ajustement pour chaque prédicteur.

• Les coefficients estimés pour chaque prédicteur. 
• r-carré du modèle, qui correspond à la proportion de variance expliquée par le modèle, et qui mesure la force de la relation entre le modèle et la variable dépendante Y sur une échelle pratique de 0 à 100 %. 
• la valeur p et la statistique t pour chaque coefficient de régression du modèle. Ces deux mesures sont considérées comme le miroir l'une de l'autre et elles mesurent la mesure dans laquelle un coefficient donné est statistiquement significatif. Plus la statistique t est élevée (ce qui va de pair avec une valeur p proche de 0), plus le prédicteur est significatif, ce qui signifie qu'il doit être conservé dans le modèle. En revanche, une statistique t très faible (valeur p plus élevée) signifie que le prédicteur doit être abandonné.

Les hypothèses de régression linéaire multiple

Lors de l'élaboration d'un modèle de régression linéaire multiple, il est important de s'assurer que les hypothèses clés suivantes sont respectées.

• Les res valeurs individuelles sont normalement distribuées. Ceci peut être vérifié à l'aide d'un graphique de probabilité normale ou d'un histogramme.
• Il doit y avoir une relation lrelation linéaire entre les variables dépendantes et les variables indépendantes. Ceci peut être illustré par des diagrammes de dispersion montrant une relation linéaire ou curviligne.
• Ensuite, multicolinéarité est une autre hypothèse, qui signifie que les variables indépendantes ne sont pas fortement corrélées entre elles. La multicolinéarité rend difficile l'identification des variables qui expliquent le mieux la variable dépendante. Cette hypothèse est vérifiée en calculant une matrice des corrélations bivariées de Pearson entre toutes les variables indépendantes. S'il n'y a pas de colinéarité dans les données, toutes les valeurs doivent être inférieures à 0,8. 
• L'homoscédasticité homoscédasticité suppose que la variance des erreurs résiduelles est similaire pour toutes les valeurs de chaque variable indépendante. Une façon de le vérifier est de tracer les valeurs prédites par rapport aux valeurs résiduelles normalisées pour voir si les points sont répartis de façon égale entre toutes les valeurs des variables indépendantes.

Dans les sections suivantes, nous aborderons certaines de ces hypothèses.

Un guide pas à pas pour la régression linéaire multiple dans R

Dans cette section, nous allons nous plonger dans la mise en œuvre technique d'un modèle de régression linéaire multiple à l'aide du langage de programmation R. 

Nous utiliserons l' ensemble des données relatives à l'attrition de la clientèle de l'espace de travail de DataCamp pour estimer la valeur de la clientèle.

Qu'entend-on par valeur pour le client ? Fondamentalement, elle détermine la valeur d'un produit ou d'un service pour un client et peut être calculée comme suit : 

Customer Value = Benefit — Cost. Où le bénéfice et le coût sont, respectivement, le bénéfice et le coût d'un produit ou d'un service. 

Cette valeur est plus élevée si l'entreprise peut offrir aux consommateurs des avantages supérieurs et des coûts inférieurs ou, idéalement, une combinaison des deux.

Cette analyse peut aider l'entreprise à identifier l'opportunité de ciblage la plus prometteuse ou la meilleure action suivante en fonction de la valeur d'un client donné.

Exploration rapide des données

Nous allons donner un aperçu rapide de l'ensemble des données afin d'appliquer le prétraitement approprié avant d'ajuster le modèle.

churn_data = read_csv('data/customer_churn.csv', show_col_types = FALSE)
# Look at the first 6 observations
head(churn_data)
# Check the dimension
dim(churn_data)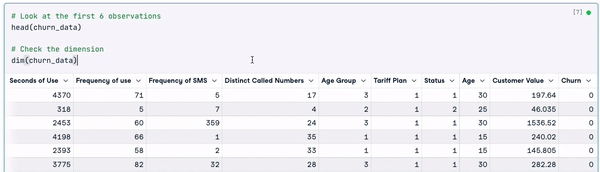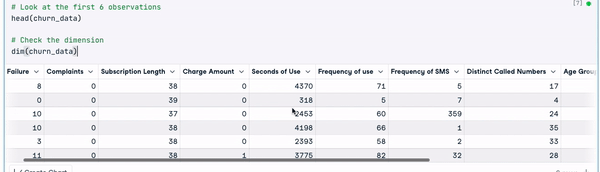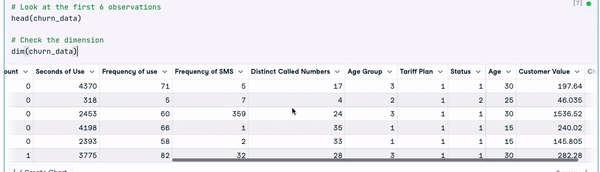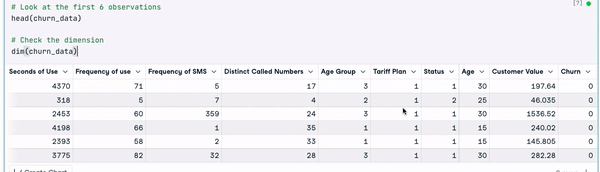

Les 6 premières lignes des données (Animation par l'auteur)

D'après les résultats précédents, nous pouvons observer que l'ensemble de données comporte 3150 observations et 14 colonnes. 

Cependant, d'après l'énoncé du problème, nous n'aurons pas besoin de la colonne "churn" car nous avons maintenant affaire à un problème de régression.

Avant d'ajuster le modèle, nous allons prétraiter les noms de colonnes en remplaçant les espaces dans les noms de colonnes par des traits de soulignement afin d'éviter d'écrire à chaque fois des guillemets doubles autour des noms de variables.

# Change the column names
names(churn_data) = gsub(" ", "_", names(churn_data))

head(churn_data)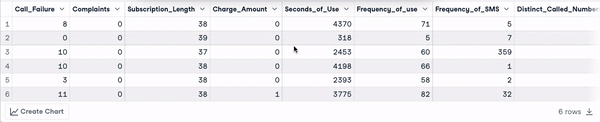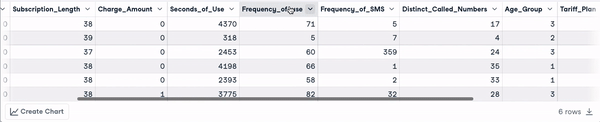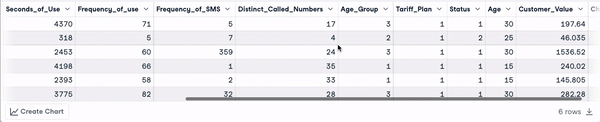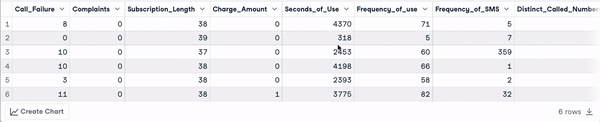

Les 6 premières lignes après la transformation des noms de colonnes (animation par l'auteur)

Avec ces données nouvellement formatées, nous pouvons les adapter au cadre de régression multiple à l'aide de la fonction lm() de R, comme suit :

# Fit the multiple linear regression model
cust_value_model = lm(formula = Customer_Value ~ Call_Failure + 

                     Complaints + Subscription_Length + Charge_Amount +    

                     Seconds_of_Use +Frequency_of_use + Frequency_of_SMS +
                    Distinct_Called_Numbers + Age_Group + Tariff_Plan +
                    Status + Age,data = churn_data)

Comprenons bien ce que nous venons de faire.

La fonction lm() se présente sous la forme suivante : lm(formula = Y ~Sum(Xi), data = our_data)

• Y est la colonne Customer_Value car c'est celle que nous essayons d'estimer.
• Sum(Xi) représente l'expression de la somme dans l'équation de régression linéaire multiple. 
• nos_données sont les données de churn.

Pour en savoir plus, consultez notre cours Régression intermédiaire en R.  

Une alternative à l'utilisation de R est la régression intermédiaire avec statsmodels en Python. Les deux vous aident à apprendre la régression linéaire et logistique avec des variables explicatives multiples.

Que nous apprend le modèle de régression linéaire multiple ?

Maintenant que nous avons construit le modèle, l'étape suivante consiste à vérifier les hypothèses et à interpréter les résultats. Par souci de simplicité, nous ne couvrirons pas tous les aspects.

Distribution des résidus du modèle 

Ceci peut être montré dans R à l'aide de la fonction hist().

# Get the model residuals
model_residuals = cust_value_model$residuals

# Plot the result
hist(model_residuals)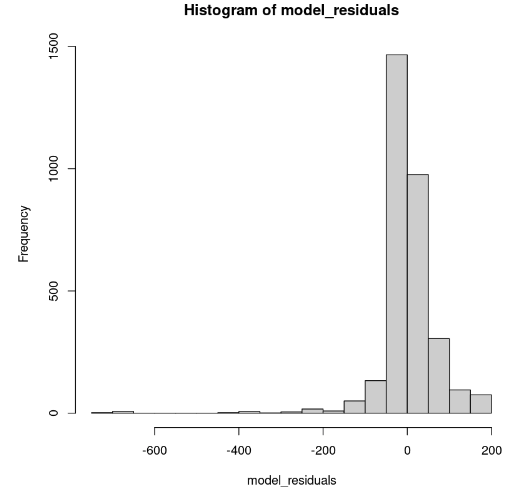

Distribution des résidus du modèle (Image de l'auteur)

L'histogramme semble asymétrique vers la gauche ; nous ne pouvons donc pas conclure à la normalité avec suffisamment de confiance. Au lieu de l'histogramme, examinons les résidus le long du graphique Q-Q normal. S'il y a normalité, les valeurs doivent suivre une ligne droite.

# Plot the residuals
qqnorm(model_residuals)
# Plot the Q-Q line
qqline(model_residuals)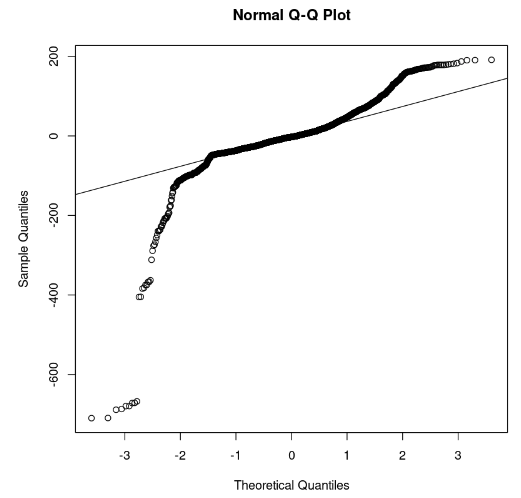

Graphique Q-Q et résidus (Image de l'auteur)

Sur le graphique, nous pouvons observer que quelques portions des résidus se situent sur une ligne droite. Nous pouvons alors supposer que les résidus du modèle ne suivent pas une distribution normale.  

Contrôle de l'hypothèse de multicolinéarité 

Pour ce faire, vous devez utiliser le code R suivant. Mais nous devons au préalable supprimer la colonne Customer_Value.

# Install and load the ggcorrplot package
install.packages("ggcorrplot")
library(ggcorrplot)

# Remove the Customer Value column
reduced_data <- subset(churn_data, select = -Customer_Value)

# Compute correlation at 2 decimal places
corr_matrix = round(cor(reduced_data), 2)

# Compute and show the  result
ggcorrplot(corr_matrix, hc.order = TRUE, type = "lower",
          lab = TRUE)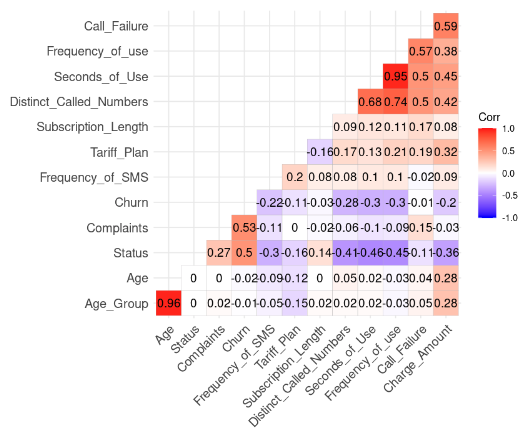

Résultat de la corrélation des données (Image de l'auteur)

Nous pouvons remarquer deux corrélations fortes car leur valeur est supérieure à 0,8. 

• Age et Age_Group : 0.96
• Fréquence d'utilisation et Seconde utilisation : 0.95

Ce résultat est logique car Age_Group est calculé à partir de Age. De même, le nombre total de secondes (Second_of_Use) est dérivé du nombre total d'appels (Frequency_of_Use). 

Dans ce cas, nous pouvons nous débarrasser de Age_Group et Second_of_Use dans l'ensemble de données. 

Essayons de construire un deuxième modèle sans ces deux variables.

second_model = lm(formula = Customer_Value ~ Call_Failure + Complaints +
                    Subscription_Length + Charge_Amount +
                    Frequency_of_use + Frequency_of_SMS +
                    Distinct_Called_Numbers + Tariff_Plan +
                    Status + Age,
                    data = churn_data)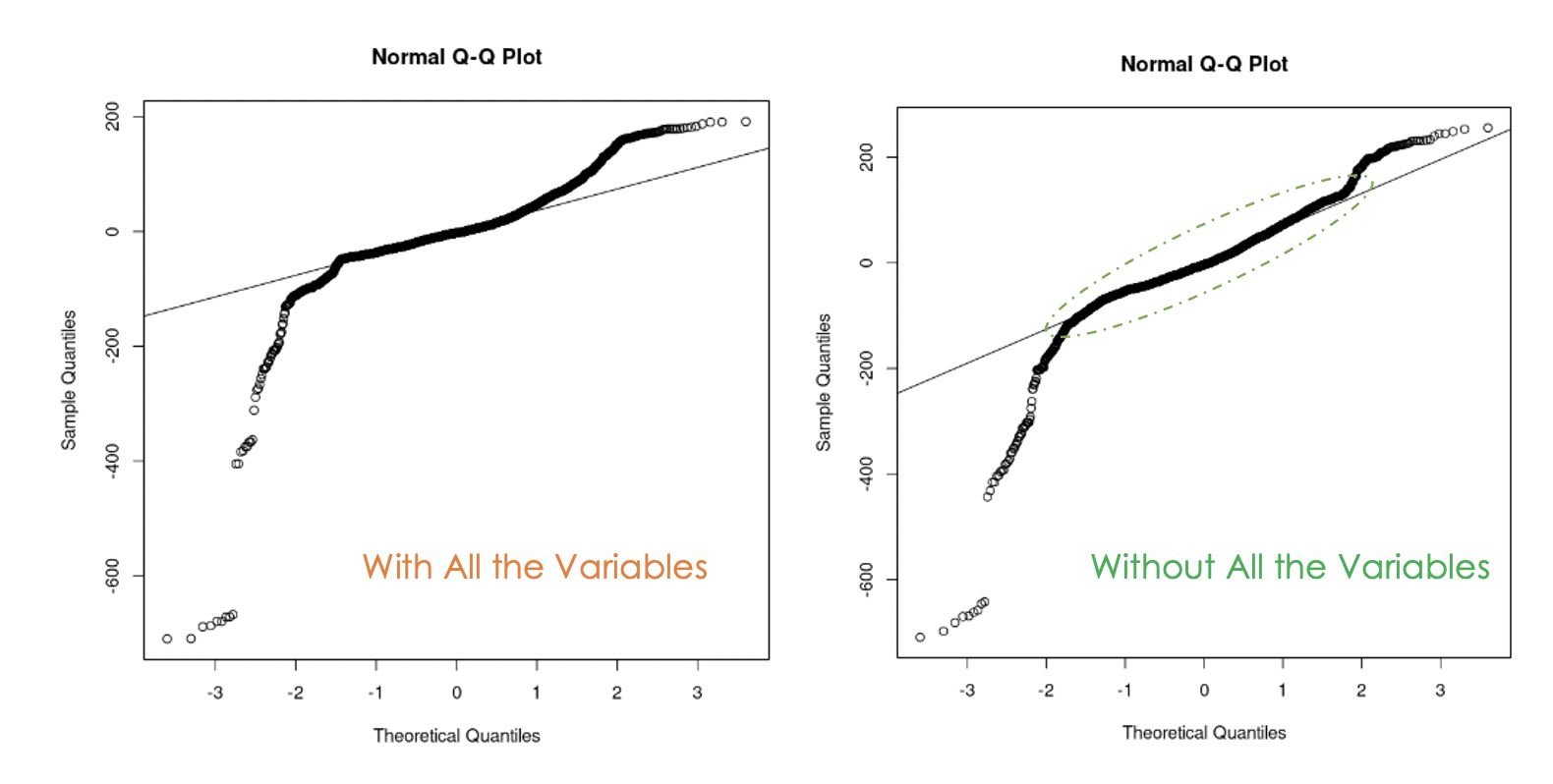

Graphiques Q-Q du premier modèle (à gauche) et du second modèle (à droite)

Nous pouvons constater que l'élimination de la multicollinéarité dans les données a été utile car, avec le deuxième modèle, davantage de valeurs résiduelles se trouvent sur la ligne droite par rapport au premier modèle.

Comment savoir lequel des deux modèles est le meilleur ? 

Une façon de répondre à cette question est d'effectuer une analyse de la variance (ANOVA) des deux modèles. Il teste l'hypothèse nulle(H0), selon laquelle les variables que nous avons supprimées précédemment ne sont pas significatives, par rapport à l'hypothèse alternative(H1) selon laquelle ces variables sont significatives. 

Si le nouveau modèle est une amélioration du modèle original, nous ne rejetons pas H0. Si ce n'est pas le cas, cela signifie que ces variables étaient significatives ; nous rejetons donc H0. 

Voici l'expression générale : anova(original_model, new_model)

# Anova test
anova(cust_value_model, second_model)

Résultat du test ANOVA (Image de l'auteur)

Le résultat de l'ANOVA montre que la valeur p (8,0893e-316) est très faible (inférieure à 0,05), de sorte que nous rejetons l'hypothèse nulle, ce qui signifie que le deuxième modèle n'améliore pas le premier. 

Une autre façon d'examiner les variables importantes du modèle est de procéder à un test de signification. 

Une variable est significative si sa valeur p est inférieure à 0,05. Ce résultat peut être généré par la fonction summary(). En plus de fournir ces informations sur le modèle, il affiche également le R-carré ajusté, qui évalue la performance des modèles les uns par rapport aux autres.

# Print the result of the model
summary(cust_value_model)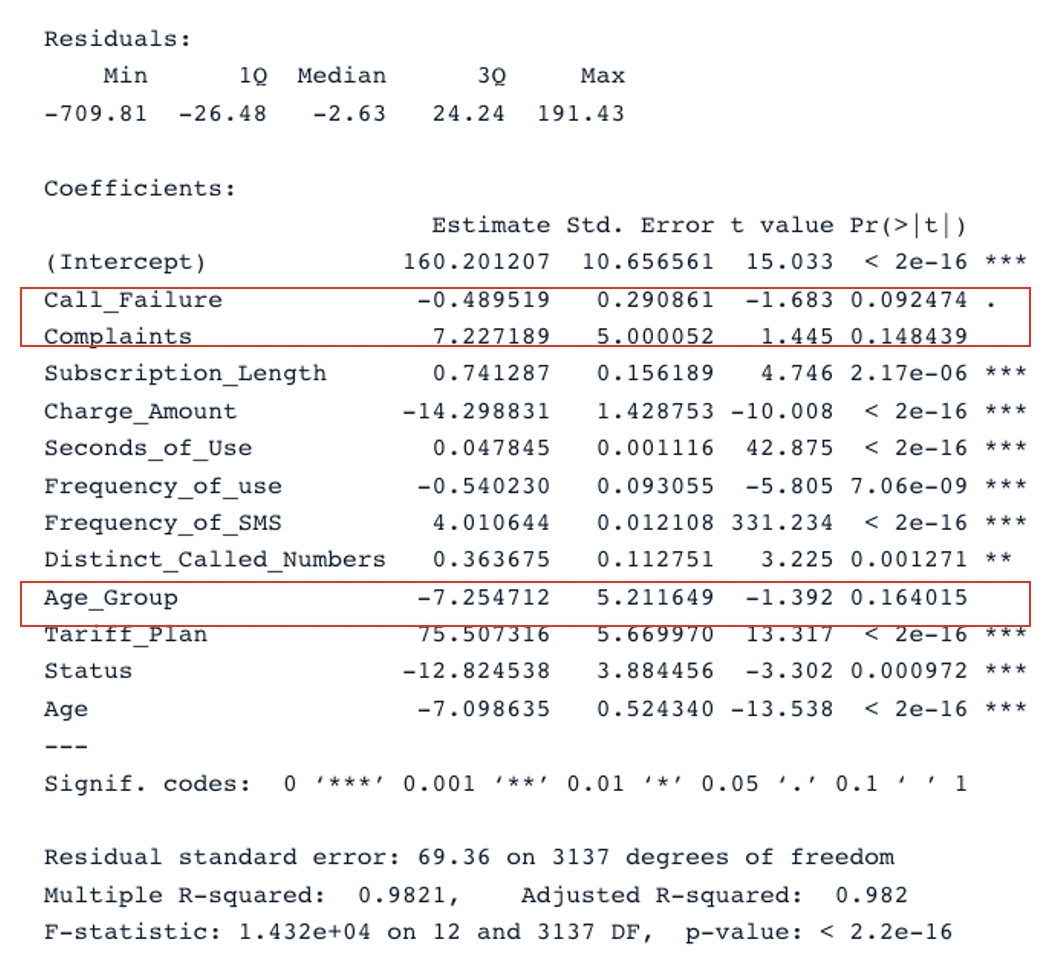

Résultat sommaire pour le modèle original avec tous les prédicteurs (Image de l'auteur)

Le tableau comporte deux sections clés : Residuals et Coefficients. Les tracés Q-Q donnent les mêmes informations que la section Residuals. Dans la section Coefficients, Call_Failure, Complaints et Age_Group ne sont pas considérés comme significatifs par le modèle car leur valeur p est supérieure à 0,05. Les conserver n'apporte aucune valeur ajoutée au modèle.

En appliquant la même analyse au deuxième modèle, nous obtenons ce résultat :

summary(second_model)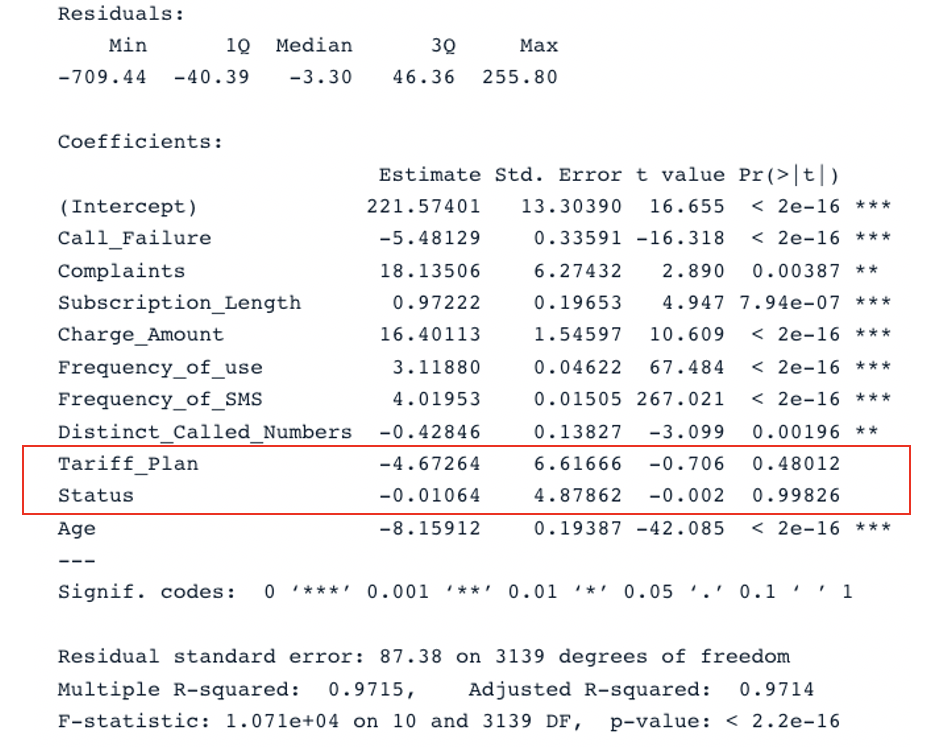

Résultat sommaire pour le deuxième modèle avec tous les prédicteurs (Image de l'auteur)

Le modèle original a un R-carré ajusté de 0,98, ce qui est plus élevé que le R-carré ajusté du second modèle (0,97). Cela signifie que le modèle original avec tous les prédicteurs est meilleur que le second modèle.

Améliorer le modèle de régression linéaire multiple

La suite logique de cette analyse consiste à supprimer les variables non significatives et à ajuster le modèle pour voir si les performances s'améliorent.

Le critère d'information d'Akaike (AIC) est une autre stratégie permettant de choisir efficacement les prédicteurs pertinents. 

Il commence par toutes les caractéristiques, puis élimine progressivement les plus mauvais prédicteurs, un par un, jusqu'à ce qu'il trouve le meilleur modèle. Plus le score AIC est faible, meilleur est le modèle. Pour ce faire, vous pouvez utiliser la fonction stepAIC().

Conclusion

Ce tutoriel a couvert les principaux aspects des régressions linéaires multiples et a exploré quelques stratégies pour construire des modèles robustes. 

Nous espérons que ce tutoriel vous permettra d'acquérir les compétences nécessaires pour obtenir des informations exploitables à partir de vos données. Vous pouvez essayer d'améliorer ces modèles en appliquant différentes approches à l'aide du code source disponible dans notre espace de travail.