Regressão linear múltipla no R: Tutorial com exemplos

Os métodos de regressão são usados em diferentes setores para entender quais variáveis afetam um determinado tópico de interesse. 

Por exemplo, os economistas podem usá-los para analisar a relação entre os gastos do consumidor e o crescimento do Produto Interno Bruto (PIB). As autoridades de saúde pública podem querer entender os custos dos indivíduos com base em suas informações históricas. Em ambos os casos, o foco não está em prever cenários individuais, mas em obter uma visão geral do relacionamento geral.

Neste artigo, começaremos fornecendo uma compreensão geral das regressões. Em seguida, explicaremos o que diferencia as regressões lineares simples e múltiplas antes de nos aprofundarmos nas implementações técnicas e fornecermos ferramentas para ajudá-lo a entender e interpretar os resultados da regressão.

O que é Regressão Linear Múltipla?

Vamos primeiro entender o que é uma regressão linear simples antes de mergulhar na regressão linear múltipla, que é apenas uma extensão da regressão linear simples.

Regressão linear simples

Uma regressão linear simples tem como objetivo modelar a relação entre a magnitude de uma única variável independente X e uma variável dependente Y, tentando estimar exatamente o quanto Y mudará quando X mudar em um determinado valor. 

• A variável independente X, também chamada de preditor, é a variável usada para fazer a previsão. 
• A variável dependente Y, também conhecida como resposta, é a que estamos tentando prever.

O aspecto "linear" da regressão linear é que estamos tentando prever Y a partir de X usando a seguinte equação "linear". 

Y = b0 + b1X 

• b0 é a interceptação da linha de regressão, correspondente ao valor previsto quando X é nulo. 
• b1 é a inclinação da linha de regressão.

Então, o que dizer da regressão linear múltipla?

Esse é o uso da regressão linear com múltiplas variáveis, e a equação é:

Y = b0 + b1X1 + b2X2 + b3X3 + … + bnXn + e

• Y e b0 são os mesmos que no modelo de regressão linear simples. 
• b1X1 representa o coeficiente de regressão (b1) sobre a primeira variável independente (X1). A mesma análise se aplica a todos os coeficientes e variáveis de regressão restantes. 
• e é o erro do modelo (resíduos), que define quanta variação é introduzida no modelo ao estimar Y.

Nem sempre podemos obter uma linha reta em um caso de regressão múltipla. No entanto, podemos controlar a forma da linha ajustando um modelo mais apropriado. 

Esses são alguns dos principais elementos computados pela regressão linear múltipla para encontrar a linha de melhor ajuste para cada preditor.

• Os coeficientes estimados para cada preditor. 
• r-quadrado do modelo, que corresponde à proporção da variação explicada pelo modelo e mede a força da relação entre o modelo e a variável dependente Y em uma escala conveniente de 0 a 100%. 
• o valor p e a estatística t para cada coeficiente de regressão no modelo. Essas duas métricas são consideradas o espelho uma da outra e medem a extensão em que um determinado coeficiente é estatisticamente significativo. Quanto maior a estatística t (que acompanha o valor p próximo de 0), mais significativo é o preditor, o que significa que esse preditor deve ser mantido no modelo. Por outro lado, uma estatística t muito baixa (valor p mais alto) significa que o preditor deve ser descartado.

Pressupostos da regressão linear múltipla

Um aspecto importante ao criar um modelo de regressão linear múltipla é garantir que as seguintes premissas principais sejam atendidas.

• O rvalores individuais são normalmente distribuídos. Isso pode ser verificado por meio de um gráfico de probabilidade normal ou de um histograma.
• Deve haver uma relação linearrelação linear entre as variáveis dependentes e independentes. Isso pode ser ilustrado por gráficos de dispersão que mostram uma relação linear ou curvilínea.
• Então, multicolinearidade é outro pressuposto, o que significa que as variáveis independentes não estão altamente correlacionadas entre si. A multicolinearidade dificulta a identificação de quais variáveis explicam melhor a variável dependente. Essa suposição é verificada pelo cálculo de uma matriz de correlações bivariadas de Pearson entre todas as variáveis independentes. Se não houver colinearidade nos dados, todos os valores deverão ser menores que 0,8. 
• A homocedasticidade pressupõe que a variância dos erros residuais seja semelhante entre os valores de cada variável independente. Uma maneira de verificar isso é por meio de um gráfico dos valores previstos em relação aos valores residuais padronizados para ver se os pontos estão igualmente distribuídos em todos os valores das variáveis independentes.

Nas próximas seções, abordaremos algumas dessas suposições.

Um guia passo a passo para regressão linear múltipla no R

Nesta seção, vamos nos aprofundar na implementação técnica de um modelo de regressão linear múltipla usando a linguagem de programação R. 

Usaremos o conjunto de dados de rotatividade de clientes do espaço de trabalho do DataCamp para estimar o valor do cliente.

O que queremos dizer com valor para o cliente? Basicamente, ele determina o valor de um produto ou serviço para um cliente, e podemos calculá-lo da seguinte forma: 

Customer Value = Benefit — Cost. Em que Benefício e Custo são, respectivamente, o benefício e o custo de um produto ou serviço. 

Esse valor será maior se a empresa puder oferecer aos consumidores benefícios mais altos e custos mais baixos ou, idealmente, uma combinação de ambos.

Essa análise pode ajudar a empresa a identificar a oportunidade de direcionamento mais promissora ou a próxima melhor ação com base no valor de um determinado cliente.

Exploração rápida de dados

Vamos ter uma visão geral rápida do conjunto de dados para que possamos aplicar o pré-processamento relevante antes de ajustar o modelo.

churn_data = read_csv('data/customer_churn.csv', show_col_types = FALSE)
# Look at the first 6 observations
head(churn_data)
# Check the dimension
dim(churn_data)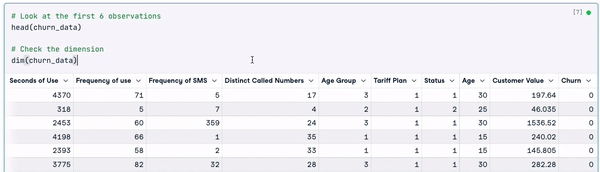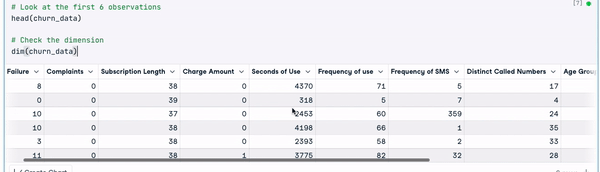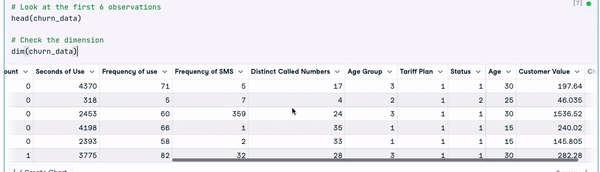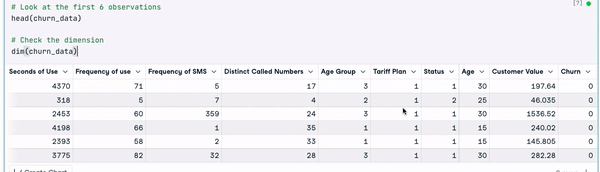

Primeiras 6 linhas dos dados (Animação do autor)

Com base nos resultados anteriores, podemos observar que o conjunto de dados tem 3150 observações e 14 colunas. 

Entretanto, com base na declaração do problema, não precisaremos da coluna de rotatividade porque agora estamos lidando com um problema de regressão.

Antes de ajustar o modelo, vamos pré-processar os nomes das colunas, substituindo os espaços nos nomes das colunas por sublinhados para evitar escrever aspas duplas ao redor dos nomes das variáveis todas as vezes.

# Change the column names
names(churn_data) = gsub(" ", "_", names(churn_data))

head(churn_data)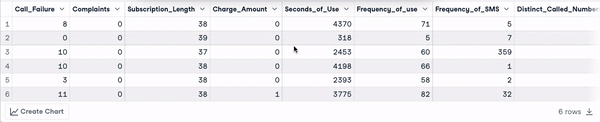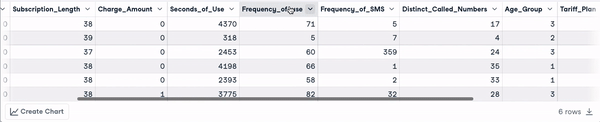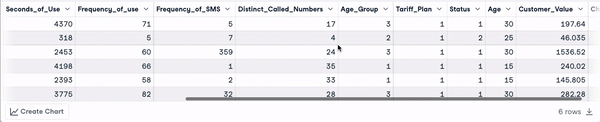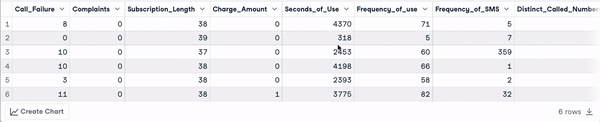

Primeiras 6 linhas após a transformação dos nomes das colunas (animação do autor)

Com esses dados recém-formatados, podemos encaixá-los na estrutura de regressão múltipla usando a função lm() no R da seguinte forma:

# Fit the multiple linear regression model
cust_value_model = lm(formula = Customer_Value ~ Call_Failure + 

                     Complaints + Subscription_Length + Charge_Amount +    

                     Seconds_of_Use +Frequency_of_use + Frequency_of_SMS +
                    Distinct_Called_Numbers + Age_Group + Tariff_Plan +
                    Status + Age,data = churn_data)

Vamos entender o que acabamos de fazer aqui.

A função lm() está no seguinte formato: lm(formula = Y ~Sum(Xi), data = our_data)

• Y é a coluna Customer_Value porque é a que estamos tentando estimar.
• Sum(Xi) representa a expressão da soma na equação de regressão linear múltipla. 
• our_data é o churn_data.

Você pode saber mais em nosso curso Intermediate Regression in R (Regressão intermediária em R ). 

Uma alternativa ao uso do R é a regressão intermediária com statsmodels em Python. Ambos ajudam você a aprender regressão linear e logística com múltiplas variáveis explicativas.

O que o modelo de regressão linear múltipla nos diz?

Agora que criamos o modelo, a próxima etapa é verificar as suposições e interpretar os resultados. Para simplificar, não abordaremos todos os aspectos.

Distribuição dos resíduos do modelo 

Isso pode ser mostrado no R usando a função hist().

# Get the model residuals
model_residuals = cust_value_model$residuals

# Plot the result
hist(model_residuals)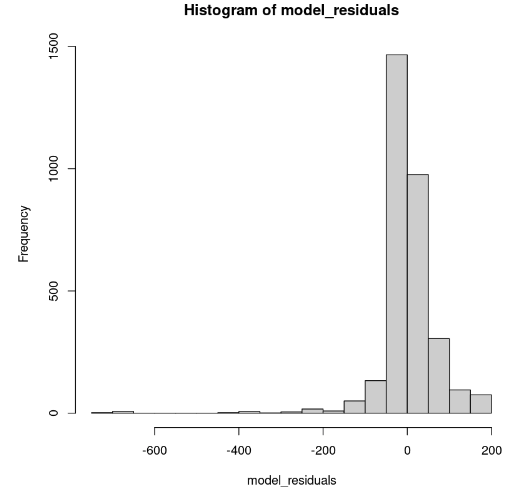

Distribuição dos resíduos do modelo (Imagem do autor)

O histograma parece inclinado para a esquerda; portanto, não podemos concluir a normalidade com confiança suficiente. Em vez do histograma, vamos examinar os resíduos ao longo do gráfico normal Q-Q. Se houver normalidade, os valores deverão seguir uma linha reta.

# Plot the residuals
qqnorm(model_residuals)
# Plot the Q-Q line
qqline(model_residuals)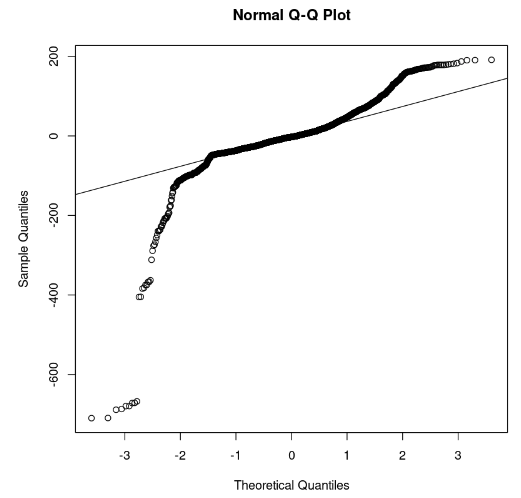

Gráfico Q-Q e resíduos (Imagem do autor)

No gráfico, podemos observar que algumas partes dos resíduos estão em uma linha reta. Então, podemos presumir que os resíduos do modelo não seguem uma distribuição normal.  

Verificação da suposição de multicolinearidade 

Isso é feito por meio do seguinte código R. Mas temos que remover a coluna Customer_Value antes.

# Install and load the ggcorrplot package
install.packages("ggcorrplot")
library(ggcorrplot)

# Remove the Customer Value column
reduced_data <- subset(churn_data, select = -Customer_Value)

# Compute correlation at 2 decimal places
corr_matrix = round(cor(reduced_data), 2)

# Compute and show the  result
ggcorrplot(corr_matrix, hc.order = TRUE, type = "lower",
          lab = TRUE)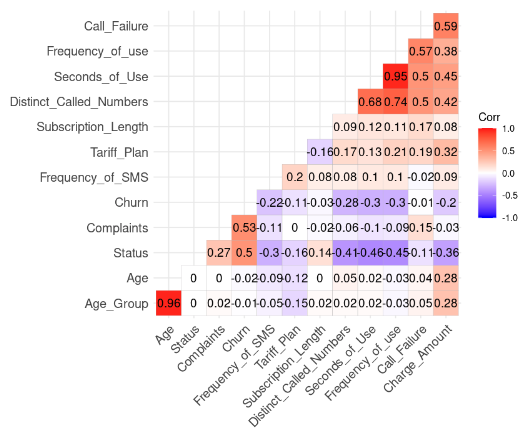

Resultado da correlação dos dados (Imagem do autor)

Podemos observar duas correlações fortes porque seu valor é superior a 0,8. 

• Idade e Age_Group: 0.96
• Frequency_of_Use e Second_of_Use: 0.95

Esse resultado faz sentido porque Age_Group é calculado a partir de Age. Além disso, o número total de segundos (Second_of_Use) é derivado do número total de chamadas (Frequency_of_Use). 

Nesse caso, podemos nos livrar de Age_Group e Second_of_Use no conjunto de dados. 

Vamos tentar criar um segundo modelo sem essas duas variáveis.

second_model = lm(formula = Customer_Value ~ Call_Failure + Complaints +
                    Subscription_Length + Charge_Amount +
                    Frequency_of_use + Frequency_of_SMS +
                    Distinct_Called_Numbers + Tariff_Plan +
                    Status + Age,
                    data = churn_data)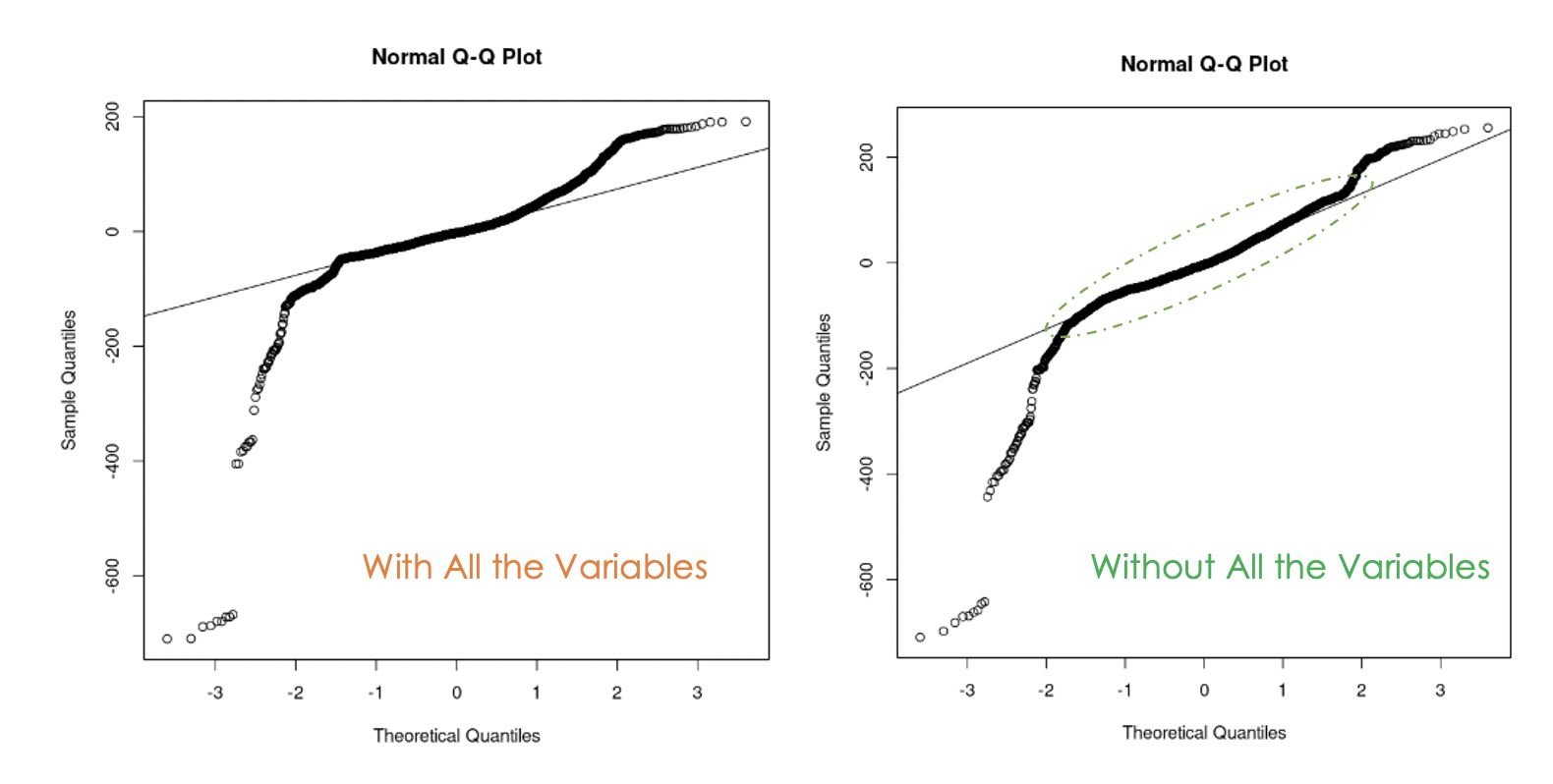

Gráficos Q-Q do primeiro modelo (esquerda) e do segundo modelo (direita)

Podemos notar que a eliminação da multicolinearidade nos dados foi útil porque, com o segundo modelo, mais valores residuais estão na linha reta em comparação com o primeiro modelo.

Como saber qual dos dois modelos é melhor? 

Uma maneira de responder a essa pergunta é executar um teste de análise de variância (ANOVA) dos dois modelos. Ele testa a hipótese nula(H0), em que as variáveis que removemos anteriormente não têm significância, contra a hipótese alternativa(H1) de que essas variáveis são significativas. 

Se o novo modelo for um aprimoramento do modelo original, então não rejeitaremos H0. Se esse não for o caso, isso significa que essas variáveis foram significativas; portanto, rejeitamos H0. 

Aqui está a expressão geral: anova(original_model, new_model)

# Anova test
anova(cust_value_model, second_model)

Resultado do teste ANOVA (Imagem do autor)

Com base no resultado da ANOVA, observamos que o valor p (8,0893e-316) é muito pequeno (menor que 0,05), portanto, rejeitamos a hipótese nula, o que significa que o segundo modelo não é um aprimoramento do primeiro. 

Outra maneira de observar as variáveis importantes no modelo é por meio de um teste de significância. 

Uma variável será significativa se seu valor de p for menor que 0,05. Esse resultado pode ser gerado pela função summary(). Além de fornecer essas informações sobre o modelo, ele também apresenta o R-quadrado ajustado, que avalia o desempenho dos modelos entre si.

# Print the result of the model
summary(cust_value_model)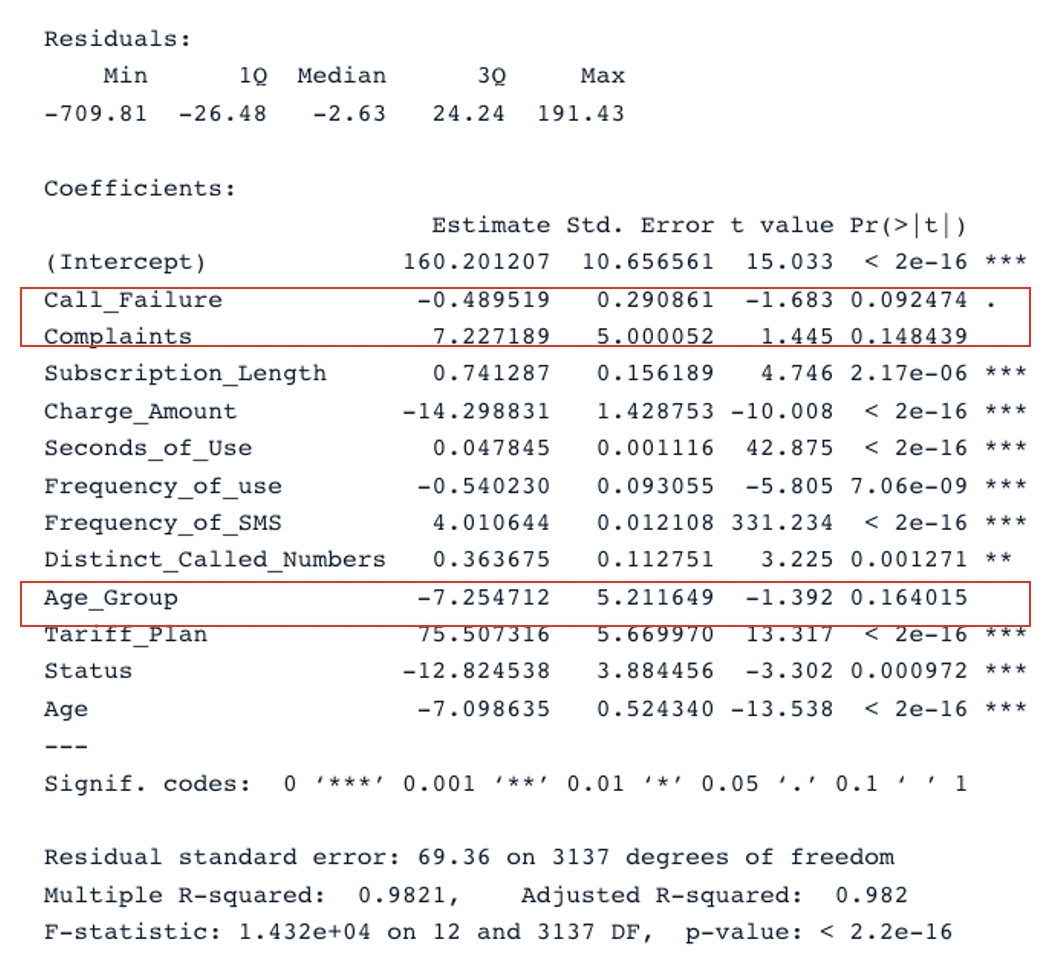

Resultado resumido para o modelo original com todos os preditores (Imagem do autor)

Temos duas seções principais na tabela: Residuals e Coefficients. Os gráficos Q-Q fornecem as mesmas informações que a seção Residuals. Na seção Coefficients, Call_Failure, Complaints e Age_Group não são considerados significativos pelo modelo porque o valor p é maior que 0,05. Mantê-los não agrega nenhum valor adicional ao modelo.

Aplicando a mesma análise ao segundo modelo, chegamos a esse resultado:

summary(second_model)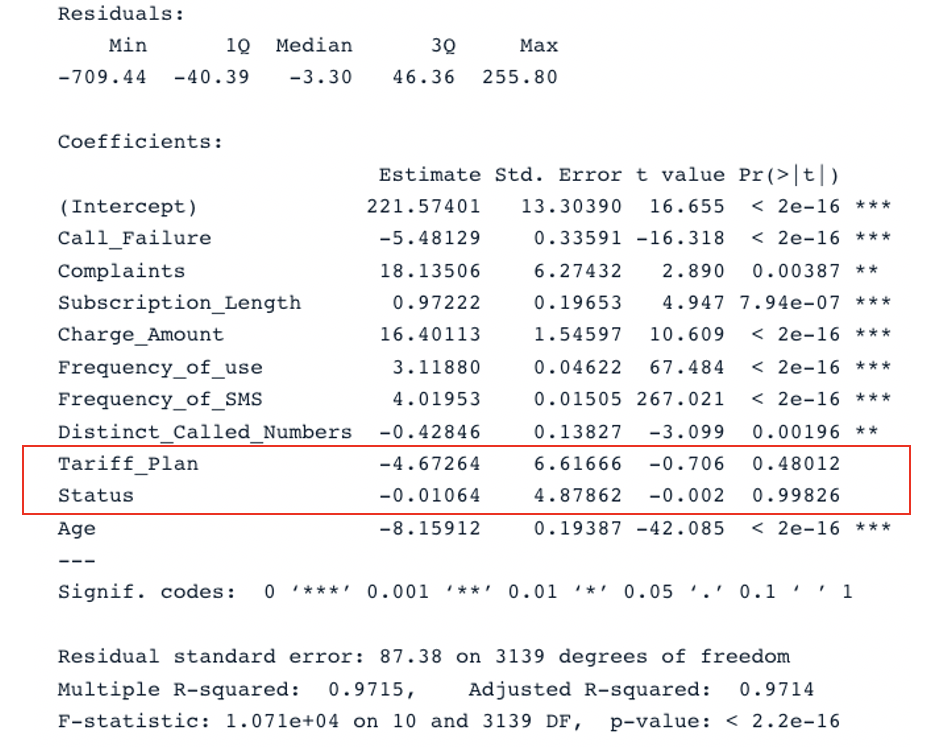

Resultado resumido para o segundo modelo com todos os preditores (Imagem do autor)

O modelo original tem um R-quadrado ajustado de 0,98, que é maior do que o R-quadrado ajustado do segundo modelo (0,97). Isso significa que o modelo original com todos os preditores é melhor do que o segundo modelo.

Aprimorar o modelo de regressão linear múltipla

A próxima etapa lógica dessa análise é remover as variáveis não significativas e ajustar o modelo para ver se o desempenho melhora.

Outra estratégia para a escolha eficiente de preditores relevantes é por meio do critério de informação de Akaike (AIC). 

Ele começa com todos os recursos e, em seguida, elimina gradualmente os piores preditores, um de cada vez, até encontrar o melhor modelo. Quanto menor for a pontuação AIC, melhor será o modelo. Isso pode ser feito usando a função stepAIC().

Conclusão

Este tutorial abordou os principais aspectos das regressões lineares múltiplas e explorou algumas estratégias para criar modelos robustos. 

Esperamos que este tutorial forneça a você as habilidades relevantes para obter insights acionáveis dos seus dados. Você pode tentar aprimorar esses modelos aplicando diferentes abordagens usando o código-fonte disponível em nosso espaço de trabalho.