Multiple lineare Regression in R: Tutorial mit Beispielen

Regressionsmethoden werden in verschiedenen Branchen eingesetzt, um zu verstehen, welche Variablen sich auf ein bestimmtes Thema von Interesse auswirken. 

Wirtschaftswissenschaftler können sie zum Beispiel nutzen, um die Beziehung zwischen den Verbraucherausgaben und dem Wachstum des Bruttoinlandsprodukts (BIP) zu analysieren. Beamte des öffentlichen Gesundheitswesens möchten vielleicht die Kosten von Einzelpersonen auf der Grundlage ihrer historischen Informationen verstehen. In beiden Fällen liegt der Schwerpunkt nicht auf der Vorhersage einzelner Szenarien, sondern darauf, einen Überblick über die Gesamtbeziehung zu bekommen.

In diesem Artikel werden wir zunächst ein allgemeines Verständnis von Regressionen vermitteln. Dann erklären wir, was den Unterschied zwischen einfachen und multiplen linearen Regressionen ausmacht, bevor wir uns mit den technischen Implementierungen befassen und Werkzeuge bereitstellen, die dir helfen, die Regressionsergebnisse zu verstehen und zu interpretieren.

Was ist multiple lineare Regression?

Verstehen wir zunächst, was eine einfache lineare Regression ist, bevor wir uns mit der multiplen linearen Regression beschäftigen, die nur eine Erweiterung der einfachen linearen Regression ist.

Einfache lineare Regression

Eine einfache lineare Regression zielt darauf ab, die Beziehung zwischen der Größe einer einzelnen unabhängigen Variable X und einer abhängigen Variable Y zu modellieren, indem versucht wird, genau abzuschätzen, wie stark sich Y ändert, wenn sich X um einen bestimmten Betrag ändert. 

• Die unabhängige Variable X, auch Prädiktor genannt, ist die Variable, die für die Vorhersage verwendet wird. 
• Die abhängige Variable Y, auch bekannt als Antwort, ist diejenige, die wir vorhersagen wollen.

Der "lineare" Aspekt der linearen Regression besteht darin, dass wir versuchen, Y anhand der folgenden "linearen" Gleichung aus X vorherzusagen. 

Y = b0 + b1X 

• b0 ist der Achsenabschnitt der Regressionsgeraden, der dem vorhergesagten Wert entspricht, wenn X Null ist. 
• b1 ist die Steigung der Regressionsgeraden.

Und was ist mit der multiplen linearen Regression?

Dies ist die Anwendung der linearen Regression mit mehreren Variablen, und die Gleichung lautet:

Y = b0 + b1X1 + b2X2 + b3X3 + … + bnXn + e

• Y und b0 sind die gleichen wie im einfachen linearen Regressionsmodell. 
• b1X1 ist der Regressionskoeffizient (b1) für die erste unabhängige Variable (X1). Die gleiche Analyse gilt für alle übrigen Regressionskoeffizienten und Variablen. 
• e ist der Modellfehler (Residuen), der angibt, wie viel Variation bei der Schätzung von Y in das Modell eingeführt wird.

Bei einer multiplen Regression erhalten wir vielleicht nicht immer eine gerade Linie. Wir können jedoch die Form der Linie kontrollieren, indem wir ein geeigneteres Modell anpassen. 

Dies sind einige der Schlüsselelemente, die bei der multiplen linearen Regression berechnet werden, um die beste Anpassungslinie für jeden Prädiktor zu finden.

• Die geschätzten Koeffizienten für jeden Prädiktor. 
• r-Quadrat des Modells, das dem Anteil der durch das Modell erklärten Varianz entspricht und die Stärke der Beziehung zwischen dem Modell und der abhängigen Variable Y auf einer praktischen Skala von 0 bis 100 % misst. 
• den p-Wert und die t-Statistik für jeden Regressionskoeffizienten des Modells. Diese beiden Messgrößen gelten als Spiegelbild voneinander und messen, inwieweit ein bestimmter Koeffizient statistisch signifikant ist. Je höher die t-Statistik (die mit dem p-Wert nahe 0 einhergeht), desto signifikanter ist der Prädiktor, was bedeutet, dass dieser Prädiktor im Modell beibehalten werden sollte. Andererseits bedeutet eine sehr niedrige t-Statistik (höherer p-Wert), dass der Prädiktor fallen gelassen werden sollte.

Die Annahmen der multiplen linearen Regression

Ein wichtiger Aspekt bei der Erstellung eines multiplen linearen Regressionsmodells ist es, sicherzustellen, dass die folgenden Schlüsselannahmen erfüllt sind.

• Die residuelle Werte sind normal verteilt. Dies kann entweder mit einem normalen Wahrscheinlichkeitsdiagramm oder einem Histogramm überprüft werden.
• Es muss eine llineare Beziehung zwischen den abhängigen und den unabhängigen Variablen bestehen. Dies kann durch Streudiagramme veranschaulicht werden, die eine lineare oder kurvenförmige Beziehung zeigen.
• Dann, Multikollinearität ist eine weitere Annahme, die besagt, dass die unabhängigen Variablen nicht stark miteinander korreliert sind. Multikollinearität macht es schwierig zu erkennen, welche Variablen die abhängige Variable besser erklären. Diese Annahme wird überprüft, indem eine Matrix der bivariaten Pearson-Korrelationen zwischen allen unabhängigen Variablen berechnet wird. Wenn es keine Kollinearität in den Daten gibt, sollten alle Werte kleiner als 0,8 sein. 
• Die Homoskedastizität geht davon aus, dass die Varianz der Restfehler über die Werte der einzelnen unabhängigen Variablen hinweg ähnlich ist. Eine Möglichkeit, dies zu überprüfen, besteht darin, die vorhergesagten Werte mit den standardisierten Restwerten zu vergleichen, um zu sehen, ob die Punkte gleichmäßig über alle Werte der unabhängigen Variablen verteilt sind.

In den nächsten Abschnitten werden wir einige dieser Annahmen behandeln.

Eine Schritt-für-Schritt-Anleitung zur multiplen linearen Regression in R

In diesem Abschnitt werden wir uns mit der technischen Umsetzung eines multiplen linearen Regressionsmodells mit der Programmiersprache R beschäftigen. 

Wir werden den Datensatz zur Kundenabwanderung aus dem DataCamp-Arbeitsbereich verwenden, um den Kundenwert zu schätzen.

Was verstehen wir unter Kundennutzen? Im Grunde genommen bestimmt sie, wie viel ein Produkt oder eine Dienstleistung für einen Kunden wert ist, und wir können sie wie folgt berechnen: 

Customer Value = Benefit — Cost. Nutzen und Kosten bezeichnen den Nutzen bzw. die Kosten eines Produkts oder einer Dienstleistung. 

Dieser Wert ist höher, wenn das Unternehmen den Verbrauchern einen höheren Nutzen und niedrigere Kosten oder idealerweise eine Kombination aus beidem bieten kann.

Diese Analyse kann dem Unternehmen dabei helfen, die vielversprechendste Targeting-Möglichkeit oder die nächstbeste Aktion auf der Grundlage des Wertes eines bestimmten Kunden zu ermitteln.

Schnelle Datenexploration

Verschaffen wir uns einen schnellen Überblick über den Datensatz, damit wir vor der Anpassung des Modells die entsprechenden Vorverarbeitungen vornehmen können.

churn_data = read_csv('data/customer_churn.csv', show_col_types = FALSE)
# Look at the first 6 observations
head(churn_data)
# Check the dimension
dim(churn_data)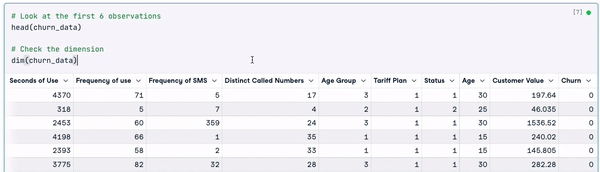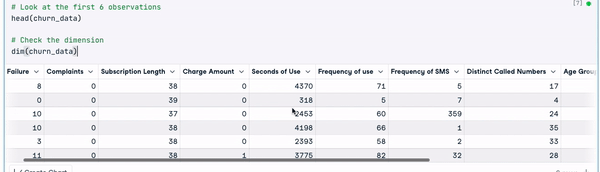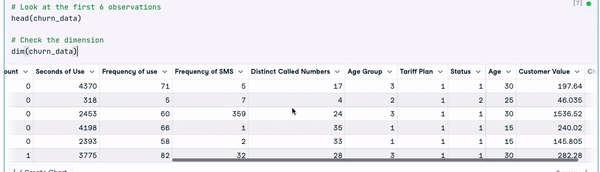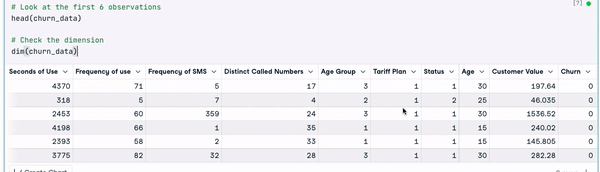

Die ersten 6 Zeilen der Daten (Animation vom Autor)

Anhand der vorherigen Ergebnisse können wir feststellen, dass der Datensatz 3150 Beobachtungen und 14 Spalten umfasst. 

Ausgehend von der Problemstellung brauchen wir die Churn-Spalte jedoch nicht, da wir es jetzt mit einem Regressionsproblem zu tun haben.

Bevor wir das Modell anpassen, bereiten wir die Spaltennamen vor, indem wir Leerzeichen in den Spaltennamen durch Unterstriche ersetzen, um zu vermeiden, dass die Variablennamen jedes Mal in Anführungszeichen gesetzt werden.

# Change the column names
names(churn_data) = gsub(" ", "_", names(churn_data))

head(churn_data)

Die ersten 6 Zeilen nach der Umwandlung der Spaltennamen (Animation des Autors)

Mit diesen neu formatierten Daten können wir sie mit der Funktion lm() in R wie folgt an die multiple Regression anpassen:

# Fit the multiple linear regression model
cust_value_model = lm(formula = Customer_Value ~ Call_Failure + 

                     Complaints + Subscription_Length + Charge_Amount +    

                     Seconds_of_Use +Frequency_of_use + Frequency_of_SMS +
                    Distinct_Called_Numbers + Age_Group + Tariff_Plan +
                    Status + Age,data = churn_data)

Lass uns verstehen, was wir hier gerade getan haben.

Die lm() Funktion hat das folgende Format: lm(formula = Y ~Sum(Xi), data = our_data)

• Y ist die Spalte "Customer_Value", denn sie ist die Spalte, die wir schätzen wollen.
• Sum(Xi) ist der Summenausdruck in der multiplen linearen Regressionsgleichung. 
• our_data sind die churn_data.

Mehr dazu erfährst du in unserem Kurs Intermediate Regression in R. 

Eine Alternative zur Verwendung von R ist die Intermediate Regression mit statsmodels in Python. Beide helfen dir, die lineare und logistische Regression mit mehreren erklärenden Variablen zu lernen.

Was sagt uns das Modell der multiplen linearen Regression?

Nachdem wir nun das Modell erstellt haben, müssen wir im nächsten Schritt die Annahmen überprüfen und die Ergebnisse interpretieren. Der Einfachheit halber werden wir nicht auf alle Aspekte eingehen.

Verteilung der Modellresiduen 

Dies kann in R mit der Funktion hist() dargestellt werden.

# Get the model residuals
model_residuals = cust_value_model$residuals

# Plot the result
hist(model_residuals)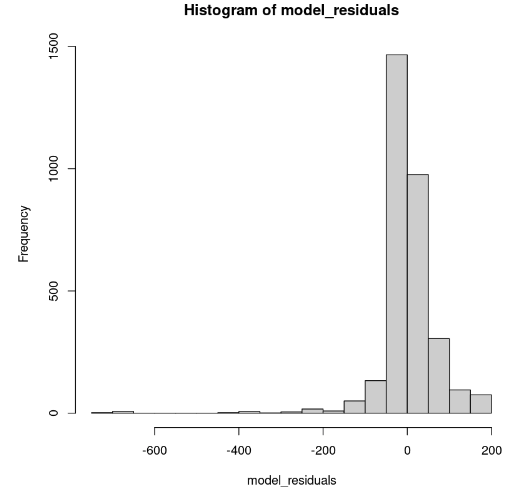

Verteilung der Modellresiduen (Bild vom Autor)

Das Histogramm sieht schief nach links aus; daher können wir nicht mit ausreichender Sicherheit auf die Normalität schließen. Anstelle des Histogramms können wir uns die Residuen entlang des normalen Q-Q-Plots ansehen. Wenn eine Normalität vorliegt, sollten die Werte einer geraden Linie folgen.

# Plot the residuals
qqnorm(model_residuals)
# Plot the Q-Q line
qqline(model_residuals)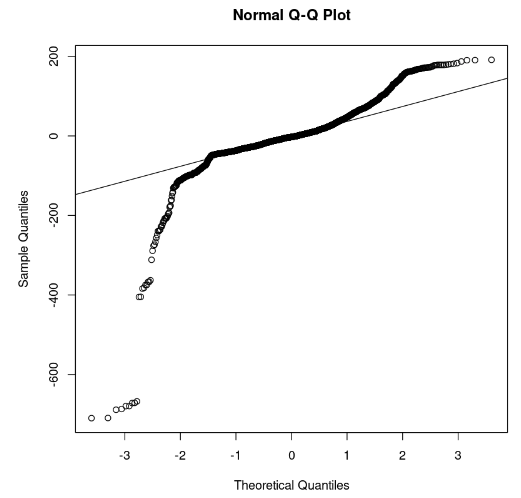

Q-Q-Plot und Residuen (Bild vom Autor)

Aus der Grafik können wir ersehen, dass einige Teile der Residuen auf einer geraden Linie liegen. Dann können wir davon ausgehen, dass die Residuen des Modells nicht einer Normalverteilung folgen.  

Prüfung der Multikollinearitätsannahme 

Dies geschieht durch den folgenden R-Code. Aber wir müssen vorher die Spalte Customer_Value entfernen.

# Install and load the ggcorrplot package
install.packages("ggcorrplot")
library(ggcorrplot)

# Remove the Customer Value column
reduced_data <- subset(churn_data, select = -Customer_Value)

# Compute correlation at 2 decimal places
corr_matrix = round(cor(reduced_data), 2)

# Compute and show the  result
ggcorrplot(corr_matrix, hc.order = TRUE, type = "lower",
          lab = TRUE)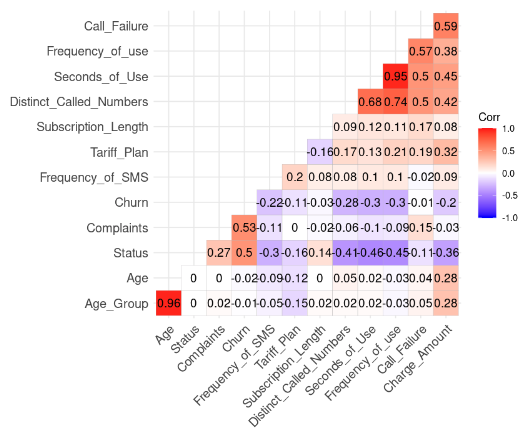

Korrelationsergebnis aus den Daten (Bild vom Autor)

Wir können zwei starke Korrelationen feststellen, da ihr Wert höher als 0,8 ist. 

• Alter und Alter_Gruppe: 0.96
• Frequency_of_Use and Second_of_Use: 0.95

Dieses Ergebnis ist sinnvoll, weil Age_Group aus Age berechnet wird. Außerdem wird die Gesamtzahl der Sekunden (Second_of_Use) von der Gesamtzahl der Anrufe (Frequency_of_Use) abgeleitet. 

In diesem Fall können wir die Altersgruppe und den zweiten Verwendungszweck im Datensatz loswerden. 

Versuchen wir nun, ein zweites Modell ohne diese beiden Variablen zu erstellen.

second_model = lm(formula = Customer_Value ~ Call_Failure + Complaints +
                    Subscription_Length + Charge_Amount +
                    Frequency_of_use + Frequency_of_SMS +
                    Distinct_Called_Numbers + Tariff_Plan +
                    Status + Age,
                    data = churn_data)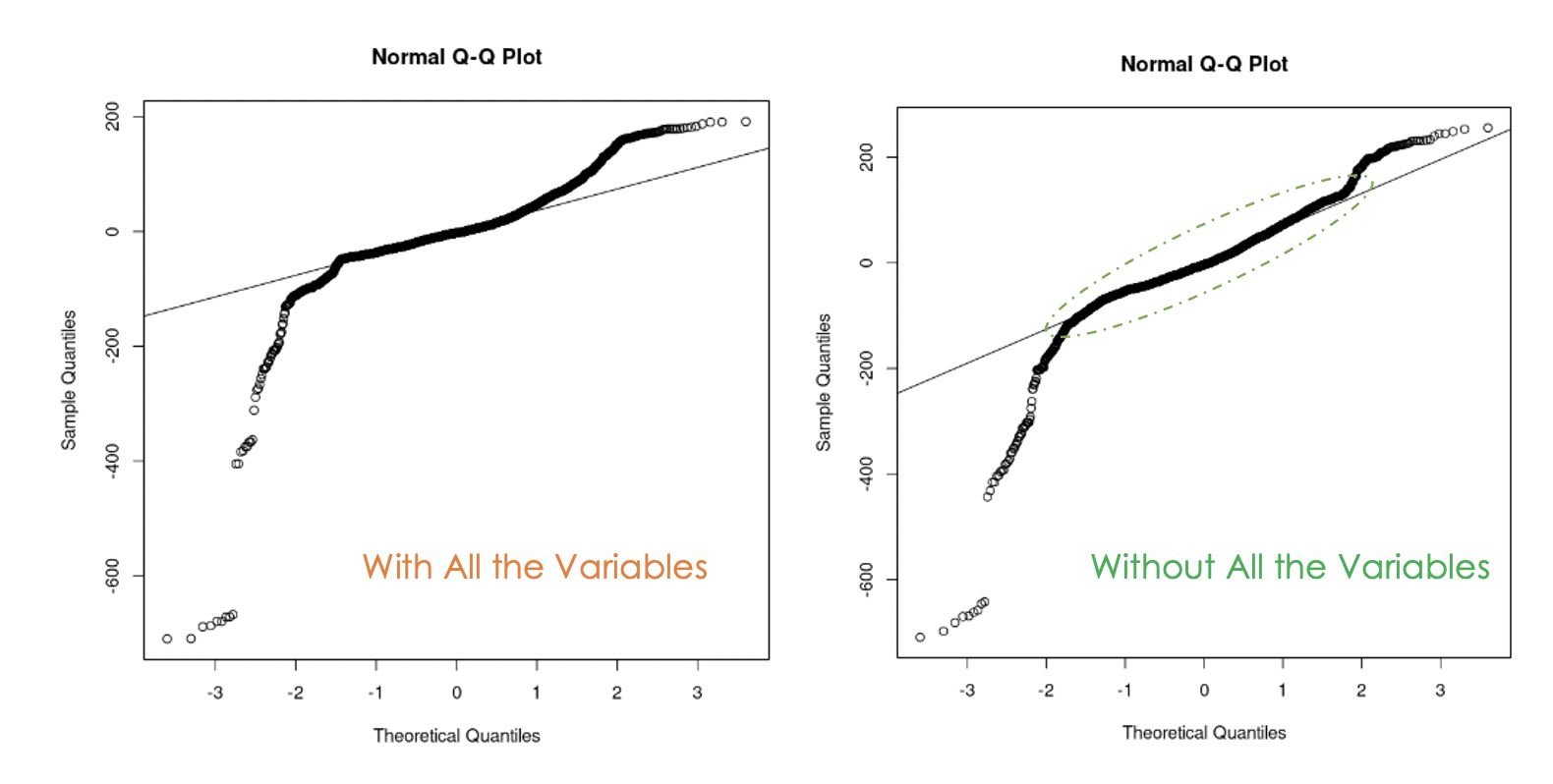

Q-Q-Diagramme für das erste Modell (links) und das zweite Modell (rechts)

Wir können feststellen, dass es hilfreich war, die Multikollinearität in den Daten zu beseitigen, denn beim zweiten Modell liegen mehr Restwerte auf der Geraden als beim ersten Modell.

Woher weiß man, welches der beiden Modelle besser ist? 

Eine Möglichkeit, diese Frage zu beantworten, besteht darin, eine Varianzanalyse (ANOVA) der beiden Modelle durchzuführen. Sie testet die Nullhypothese(H0), dass die Variablen, die wir zuvor entfernt haben, nicht signifikant sind, gegen die Alternativhypothese(H1), dass diese Variablen signifikant sind. 

Wenn das neue Modell eine Verbesserung des ursprünglichen Modells ist, dann können wir H0 nicht zurückweisen. Wenn das nicht der Fall ist, bedeutet das, dass diese Variablen signifikant waren; daher verwerfen wir H0. 

Hier ist der allgemeine Ausdruck: anova(original_model, new_model)

# Anova test
anova(cust_value_model, second_model)

ANOVA-Testergebnis (Bild vom Autor)

Anhand des ANOVA-Ergebnisses stellen wir fest, dass der p-Wert (8,0893e-316) sehr klein ist (weniger als 0,05), sodass wir die Nullhypothese ablehnen, was bedeutet, dass das zweite Modell keine Verbesserung des ersten darstellt. 

Eine andere Möglichkeit, die wichtigen Variablen des Modells zu untersuchen, ist ein Signifikanztest. 

Eine Variable ist signifikant, wenn ihr p-Wert kleiner als 0,05 ist. Dieses Ergebnis kann mit der Funktion summary() erzeugt werden. Zusätzlich zu diesen Informationen über das Modell wird auch das bereinigte R-Quadrat angezeigt, das die Leistung der Modelle gegeneinander abwägt.

# Print the result of the model
summary(cust_value_model)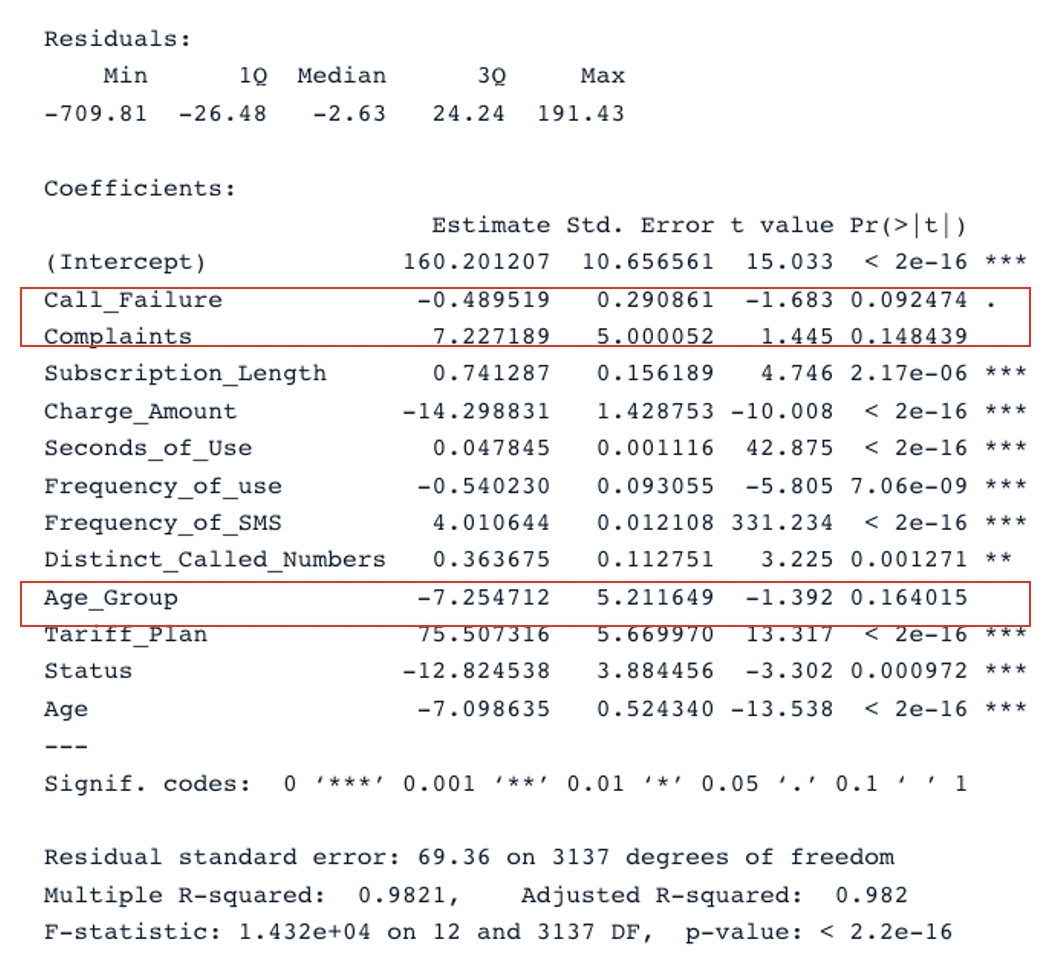

Zusammenfassendes Ergebnis für das ursprüngliche Modell mit allen Prädiktoren (Bild vom Autor)

Wir haben zwei wichtige Abschnitte in der Tabelle: Residuals und Coefficients. Die Q-Q-Diagramme geben die gleichen Informationen wie der Abschnitt Residuals. Im Abschnitt Coefficients werden Call_Failure, Complaints und Age_Group von dem Modell nicht als signifikant angesehen, da ihr p-Wert über 0,05 liegt. Sie zu behalten, bringt dem Modell keinen zusätzlichen Wert.

Wendet man die gleiche Analyse auf das zweite Modell an, kommt man zu diesem Ergebnis:

summary(second_model)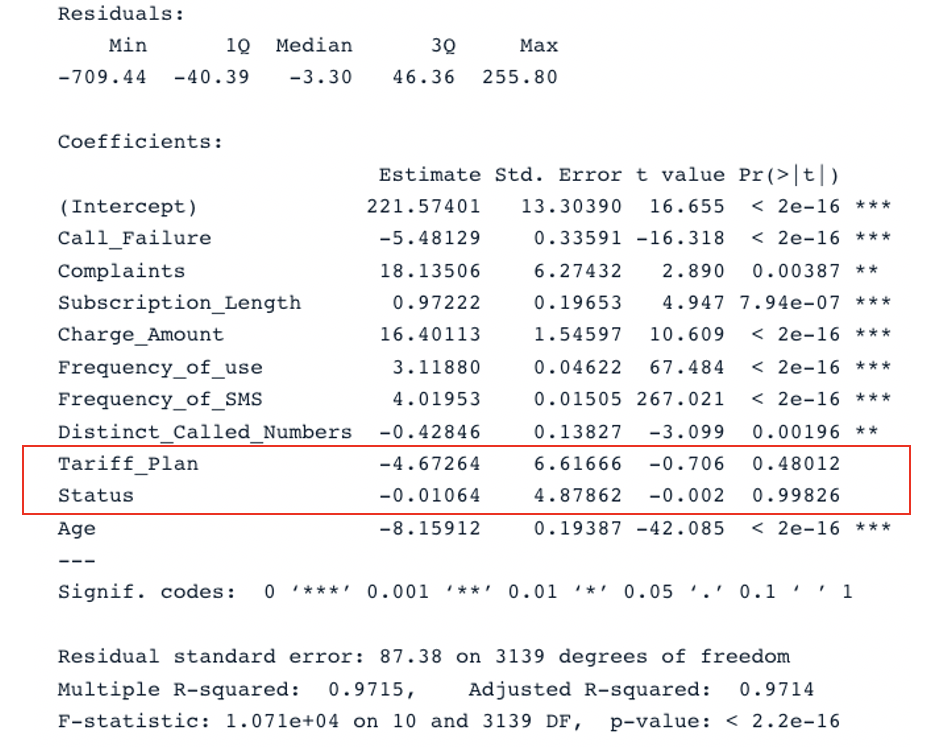

Zusammenfassendes Ergebnis für das zweite Modell mit allen Prädiktoren (Bild vom Autor)

Das ursprüngliche Modell hat ein bereinigtes R-Quadrat von 0,98, das höher ist als das bereinigte R-Quadrat des zweiten Modells (0,97). Das bedeutet, dass das ursprüngliche Modell mit allen Prädiktoren besser ist als das zweite Modell.

Verbessere das Modell der multiplen linearen Regression

Der logische nächste Schritt dieser Analyse besteht darin, die nicht signifikanten Variablen zu entfernen und das Modell anzupassen, um zu sehen, ob sich die Leistung verbessert.

Eine weitere Strategie zur effizienten Auswahl relevanter Prädiktoren ist das Akaike-Informationskriterium (AIC). 

Er beginnt mit allen Merkmalen und lässt dann nach und nach die schlechtesten Prädiktoren fallen, bis er das beste Modell gefunden hat. Je kleiner der AIC-Wert ist, desto besser ist das Modell. Das kannst du mit der Funktion stepAIC() machen.

Fazit

In diesem Tutorium wurden die wichtigsten Aspekte der multiplen linearen Regressionen behandelt und einige Strategien zur Erstellung robuster Modelle untersucht. 

Wir hoffen, dass dieses Tutorial dir die nötigen Fähigkeiten vermittelt, um aus deinen Daten verwertbare Erkenntnisse zu gewinnen. Du kannst versuchen, diese Modelle zu verbessern, indem du verschiedene Ansätze anwendest und den Quellcode in unserem Arbeitsbereich verwendest.