Tutoriel sur les machines à vecteurs de support avec Scikit-learn

Le SVM est un algorithme passionnant dont les concepts sont relativement simples. Le classificateur sépare les points de données à l'aide d'un hyperplan ayant la plus grande marge. C'est pourquoi un classificateur SVM est également connu sous le nom de classificateur discriminant. Le SVM trouve un hyperplan optimal qui aide à classer les nouveaux points de données.

Dans ce tutoriel, vous allez couvrir les sujets suivants :

• Machines à vecteurs de support
• Comment cela fonctionne-t-il ?
• Noyaux
• Construction d'un classificateur dans Scikit-learn
• Réglage des hyperparamètres
• Avantages et inconvénients

Regardez et apprenez-en plus sur les machines à vecteurs de support avec Scikit-learn dans cette vidéo de notre cours.

Machines à vecteurs de support

Généralement, les machines à vecteurs de support sont considérées comme une approche de classification, mais elles peuvent être employées dans les deux types de problèmes de classification et de régression. Il peut facilement traiter plusieurs variables continues et catégorielles. Les SVM construisent un hyperplan dans un espace multidimensionnel pour séparer les différentes classes. Le SVM génère un hyperplan optimal de manière itérative, qui est utilisé pour minimiser l'erreur. L'idée centrale des SVM est de trouver un hyperplan marginal maximal (MMH) qui divise au mieux l'ensemble de données en classes.

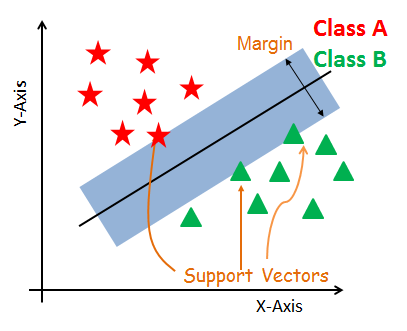
Vecteurs de soutien

Les vecteurs de soutien sont les points de données les plus proches de l'hyperplan. Ces points permettront de mieux définir la ligne de séparation en calculant les marges. Ces points sont plus pertinents pour la construction du classificateur.

Hyperplan

Un hyperplan est un plan de décision qui sépare un ensemble d'objets appartenant à des classes différentes.

Marge

Une marge est un espace entre les deux lignes des points de classe les plus proches. Il s'agit de la distance perpendiculaire entre la ligne et les vecteurs de support ou les points les plus proches. Si la marge est plus grande entre les classes, elle est considérée comme une bonne marge, une marge plus petite est considérée comme une mauvaise marge.

Comment fonctionne le SVM ?

L'objectif principal est de séparer l'ensemble de données donné de la meilleure façon possible. La distance entre les deux points les plus proches est appelée marge. L'objectif est de sélectionner un hyperplan avec la plus grande marge possible entre les vecteurs de support dans l'ensemble de données donné. Le SVM recherche l'hyperplan marginal maximal dans les étapes suivantes :

1. Générer des hyperplans qui séparent les classes de la meilleure façon. Figure de gauche montrant trois hyperplans noir, bleu et orange. Ici, le bleu et l'orange ont une erreur de classification plus élevée, mais le noir sépare correctement les deux classes.

2. Sélectionnez l'hyperplan de droite avec la ségrégation maximale à partir des deux points de données les plus proches, comme le montre la figure de droite.

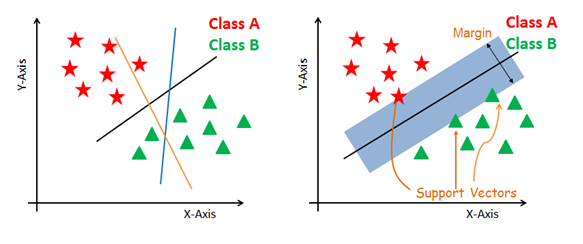
Traitement des plans non linéaires et inséparables

Certains problèmes ne peuvent pas être résolus à l'aide d'un hyperplan linéaire, comme le montre la figure ci-dessous (partie gauche).

Dans ce cas, le SVM utilise un noyau pour transformer l'espace d'entrée en un espace de dimension supérieure, comme indiqué à droite. Les points de données sont représentés sur l'axe des x et l'axe des z (Z est la somme quadratique de x et y : z=x^2=y^2). Vous pouvez maintenant facilement séparer ces points à l'aide de la séparation linéaire.

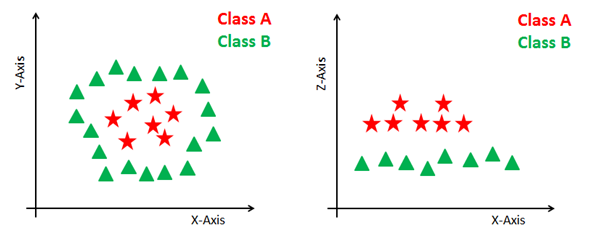
Noyaux SVM

L'algorithme SVM est mis en œuvre dans la pratique à l'aide d'un noyau. Un noyau transforme un espace de données d'entrée dans la forme requise. Les SVM utilisent une technique appelée "astuce du noyau". Ici, le noyau prend un espace d'entrée de faible dimension et le transforme en un espace de dimension supérieure. En d'autres termes, on peut dire qu'il convertit des problèmes non séparables en problèmes séparables en leur ajoutant une dimension supplémentaire. Il est particulièrement utile pour les problèmes de séparation non linéaires. L'astuce du noyau vous permet de construire un classificateur plus précis.

• Noyau linéaire Un noyau linéaire peut être utilisé comme produit de points normaux pour deux observations données. Le produit entre deux vecteurs est la somme de la multiplication de chaque paire de valeurs d'entrée.

K(x, xi) = sum(x * xi)

• Noyau polynomial Un noyau polynomial est une forme plus généralisée du noyau linéaire. Le noyau polynomial permet de distinguer les espaces d'entrée courbes ou non linéaires.

K(x,xi) = 1 + sum(x * xi)^d

Où d est le degré du polynôme. d=1 est similaire à la transformation linéaire. Le degré doit être spécifié manuellement dans l'algorithme d'apprentissage.

• Noyau de la fonction de base radiale Le noyau de la fonction de base radiale est une fonction de noyau populaire couramment utilisée dans la classification par machine à vecteur de support. La méthode RBF permet de cartographier un espace d'entrée dans un espace de dimension infinie.

K(x,xi) = exp(-gamma * sum((x – xi^2))

Ici, gamma est un paramètre compris entre 0 et 1. Une valeur plus élevée de gamma correspondra parfaitement à l'ensemble des données d'apprentissage, ce qui entraînera un surajustement. Gamma=0,1 est considéré comme une bonne valeur par défaut. La valeur de gamma doit être spécifiée manuellement dans l'algorithme d'apprentissage.

Construction d'un classificateur dans Scikit-learn

Jusqu'à présent, vous avez appris les fondements théoriques des SVM. Vous allez maintenant découvrir sa mise en œuvre en Python à l'aide de scikit-learn.

Pour la construction du modèle, vous pouvez utiliser l'ensemble de données sur le cancer, qui est un problème de classification multi-classes très connu. Cet ensemble de données est calculé à partir d'une image numérisée d'une aspiration à l'aiguille fine (AAF) d'une masse mammaire. Ils décrivent les caractéristiques des noyaux cellulaires présents dans l'image.

L'ensemble de données comprend 30 caractéristiques (rayon moyen, texture moyenne, périmètre moyen, surface moyenne, douceur moyenne, compacité moyenne, concavité moyenne, points concaves moyens, symétrie moyenne, dimension fractale moyenne, erreur de rayon, erreur de texture, erreur de périmètre, erreur de surface, erreur de douceur, erreur de compacité, erreur de symétrie, erreur de dimension fractale, pire rayon, pire texture, pire périmètre, pire surface, pire douceur, pire compacité, pire concavité, pire points concaves, pire dimension fractale), erreur de concavité, erreur de points concaves, erreur de symétrie, erreur de dimension fractale, pire rayon, pire texture, pire périmètre, pire surface, pire lissage, pire compacité, pire concavité, pire points concaves, pire symétrie et pire dimension fractale) et une cible (type de cancer).

Ces données comportent deux types de classes de cancer : les cancers malins (nocifs) et les cancers bénins (non nocifs). Ici, vous pouvez construire un modèle pour classer le type de cancer. L'ensemble de données est disponible dans la bibliothèque scikit-learn ou vous pouvez également le télécharger à partir de la bibliothèque d'apprentissage automatique de l'UCI.

Chargement des données

Commençons par charger l'ensemble de données que vous allez utiliser.

#Import scikit-learn dataset library
from sklearn import datasets

#Load dataset
cancer = datasets.load_breast_cancer()

Exploration des données

Après avoir chargé l'ensemble de données, vous voudrez peut-être en savoir un peu plus. Vous pouvez vérifier les noms des caractéristiques et des cibles.

# print the names of the 13 features
print("Features: ", cancer.feature_names)

# print the label type of cancer('malignant' 'benign')
print("Labels: ", cancer.target_names)

Features:  ['mean radius' 'mean texture' 'mean perimeter' 'mean area'
 'mean smoothness' 'mean compactness' 'mean concavity'
 'mean concave points' 'mean symmetry' 'mean fractal dimension'
 'radius error' 'texture error' 'perimeter error' 'area error'
 'smoothness error' 'compactness error' 'concavity error'
 'concave points error' 'symmetry error' 'fractal dimension error'
 'worst radius' 'worst texture' 'worst perimeter' 'worst area'
 'worst smoothness' 'worst compactness' 'worst concavity'
 'worst concave points' 'worst symmetry' 'worst fractal dimension']
Labels:  ['malignant' 'benign']

Explorons-le un peu plus en détail. Vous pouvez également vérifier la forme de l'ensemble de données à l'aide de shape.

# print data(feature)shape
cancer.data.shape

(569, 30)

Vérifions les 5 enregistrements les plus importants de l'ensemble des caractéristiques.

# print the cancer data features (top 5 records)
print(cancer.data[0:5])

[[1.799e+01 1.038e+01 1.228e+02 1.001e+03 1.184e-01 2.776e-01 3.001e-01
  1.471e-01 2.419e-01 7.871e-02 1.095e+00 9.053e-01 8.589e+00 1.534e+02
  6.399e-03 4.904e-02 5.373e-02 1.587e-02 3.003e-02 6.193e-03 2.538e+01
  1.733e+01 1.846e+02 2.019e+03 1.622e-01 6.656e-01 7.119e-01 2.654e-01
  4.601e-01 1.189e-01]
 [2.057e+01 1.777e+01 1.329e+02 1.326e+03 8.474e-02 7.864e-02 8.690e-02
  7.017e-02 1.812e-01 5.667e-02 5.435e-01 7.339e-01 3.398e+00 7.408e+01
  5.225e-03 1.308e-02 1.860e-02 1.340e-02 1.389e-02 3.532e-03 2.499e+01
  2.341e+01 1.588e+02 1.956e+03 1.238e-01 1.866e-01 2.416e-01 1.860e-01
  2.750e-01 8.902e-02]
 [1.969e+01 2.125e+01 1.300e+02 1.203e+03 1.096e-01 1.599e-01 1.974e-01
  1.279e-01 2.069e-01 5.999e-02 7.456e-01 7.869e-01 4.585e+00 9.403e+01
  6.150e-03 4.006e-02 3.832e-02 2.058e-02 2.250e-02 4.571e-03 2.357e+01
  2.553e+01 1.525e+02 1.709e+03 1.444e-01 4.245e-01 4.504e-01 2.430e-01
  3.613e-01 8.758e-02]
 [1.142e+01 2.038e+01 7.758e+01 3.861e+02 1.425e-01 2.839e-01 2.414e-01
  1.052e-01 2.597e-01 9.744e-02 4.956e-01 1.156e+00 3.445e+00 2.723e+01
  9.110e-03 7.458e-02 5.661e-02 1.867e-02 5.963e-02 9.208e-03 1.491e+01
  2.650e+01 9.887e+01 5.677e+02 2.098e-01 8.663e-01 6.869e-01 2.575e-01
  6.638e-01 1.730e-01]
 [2.029e+01 1.434e+01 1.351e+02 1.297e+03 1.003e-01 1.328e-01 1.980e-01
  1.043e-01 1.809e-01 5.883e-02 7.572e-01 7.813e-01 5.438e+00 9.444e+01
  1.149e-02 2.461e-02 5.688e-02 1.885e-02 1.756e-02 5.115e-03 2.254e+01
  1.667e+01 1.522e+02 1.575e+03 1.374e-01 2.050e-01 4.000e-01 1.625e-01
  2.364e-01 7.678e-02]]

Jetons un coup d'œil sur l'objectif fixé.

# print the cancer labels (0:malignant, 1:benign)
print(cancer.target)

[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 1 0 0 0 0 0 0 0 0 1 0 1 1 1 1 1 0 0 1 0 0 1 1 1 1 0 1 0 0 1 1 1 1 0 1 0 0
 1 0 1 0 0 1 1 1 0 0 1 0 0 0 1 1 1 0 1 1 0 0 1 1 1 0 0 1 1 1 1 0 1 1 0 1 1
 1 1 1 1 1 1 0 0 0 1 0 0 1 1 1 0 0 1 0 1 0 0 1 0 0 1 1 0 1 1 0 1 1 1 1 0 1
 1 1 1 1 1 1 1 1 0 1 1 1 1 0 0 1 0 1 1 0 0 1 1 0 0 1 1 1 1 0 1 1 0 0 0 1 0
 1 0 1 1 1 0 1 1 0 0 1 0 0 0 0 1 0 0 0 1 0 1 0 1 1 0 1 0 0 0 0 1 1 0 0 1 1
 1 0 1 1 1 1 1 0 0 1 1 0 1 1 0 0 1 0 1 1 1 1 0 1 1 1 1 1 0 1 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 1 1 1 1 1 1 0 1 0 1 1 0 1 1 0 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1
 1 0 1 1 0 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 0 1 0 1 1 1 1 0 0 0 1 1
 1 1 0 1 0 1 0 1 1 1 0 1 1 1 1 1 1 1 0 0 0 1 1 1 1 1 1 1 1 1 1 1 0 0 1 0 0
 0 1 0 0 1 1 1 1 1 0 1 1 1 1 1 0 1 1 1 0 1 1 0 0 1 1 1 1 1 1 0 1 1 1 1 1 1
 1 0 1 1 1 1 1 0 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 0 1 0 0 1 0 1 1 1 1 1 0 1 1
 0 1 0 1 1 0 1 0 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 0 1
 1 1 1 1 1 1 0 1 0 1 1 0 1 1 1 1 1 0 0 1 0 1 0 1 1 1 1 1 0 1 1 0 1 0 1 0 0
 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 0 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 1 1 1 1 1 1 1 0 0 0 0 0 0 1]

Fractionnement des données

Pour comprendre les performances d'un modèle, la division de l'ensemble de données en un ensemble d'apprentissage et un ensemble de test est une bonne stratégie.

Divisez l'ensemble de données à l'aide de la fonction train_test_split(). Vous devez passer 3 paramètres : features, target, et test_set size. En outre, vous pouvez utiliser random_state pour sélectionner des enregistrements de manière aléatoire.

# Import train_test_split function
from sklearn.model_selection import train_test_split

# Split dataset into training set and test set
X_train, X_test, y_train, y_test = train_test_split(cancer.data, cancer.target, test_size=0.3,random_state=109) # 70% training and 30% test

Générer un modèle

Construisons un modèle de machine à vecteur de support. Tout d'abord, importez le module SVM et créez un objet classificateur à vecteur de support en passant l'argument kernel comme noyau linéaire dans la fonction SVC().

Ensuite, ajustez votre modèle sur l'ensemble d'entraînement à l'aide de fit() et effectuez une prédiction sur l'ensemble de test à l'aide de predict().

#Import svm model
from sklearn import svm

#Create a svm Classifier
clf = svm.SVC(kernel='linear') # Linear Kernel

#Train the model using the training sets
clf.fit(X_train, y_train)

#Predict the response for test dataset
y_pred = clf.predict(X_test)

Évaluation du modèle

Estimons la précision avec laquelle le classificateur ou le modèle peut prédire le cancer du sein des patientes.

La précision peut être calculée en comparant les valeurs réelles de l'ensemble de tests et les valeurs prédites.

#Import scikit-learn metrics module for accuracy calculation
from sklearn import metrics

# Model Accuracy: how often is the classifier correct?
print("Accuracy:",metrics.accuracy_score(y_test, y_pred))

Accuracy: 0.9649122807017544

Vous avez obtenu un taux de classification de 96,49 %, ce qui est considéré comme une très bonne précision.

Pour une évaluation plus approfondie, vous pouvez également vérifier la précision et le rappel du modèle.

# Model Precision: what percentage of positive tuples are labeled as such?
print("Precision:",metrics.precision_score(y_test, y_pred))

# Model Recall: what percentage of positive tuples are labelled as such?
print("Recall:",metrics.recall_score(y_test, y_pred))

Precision: 0.9811320754716981
Recall: 0.9629629629629629

Vous avez obtenu une précision de 98 % et un rappel de 96 %, ce qui est considéré comme de très bonnes valeurs.

Réglage des hyperparamètres

• Noyau : La fonction principale du noyau est de transformer les données d'entrée de l'ensemble de données donné dans la forme requise. Il existe différents types de fonctions, telles que les fonctions linéaires, polynomiales et à base radiale (RBF). Le polynôme et le RBF sont utiles pour les hyperplans non linéaires. Les noyaux polynomiaux et RBF calculent la ligne de séparation dans la dimension supérieure. Dans certaines applications, il est suggéré d'utiliser un noyau plus complexe pour séparer les classes courbes ou non linéaires. Cette transformation peut conduire à des classificateurs plus précis.

• Régularisation : Paramètre de régularisation dans Scikit-learn de Python Paramètre C utilisé pour maintenir la régularisation. Ici, C est le paramètre de pénalité, qui représente la mauvaise classification ou le terme d'erreur. Le terme de mauvaise classification ou d'erreur indique à l'optimisation du SVM le niveau d'erreur supportable. C'est ainsi que vous pouvez contrôler le compromis entre la limite de décision et le terme de classification erronée. Une valeur plus petite de C crée un hyperplan à petite marge et une valeur plus grande de C crée un hyperplan à grande marge.
• Gamma : Une valeur faible de Gamma correspondra à un ajustement approximatif de l'ensemble des données d'apprentissage, tandis qu'une valeur élevée de Gamma correspondra exactement à l'ensemble des données d'apprentissage, ce qui entraîne un surajustement. En d'autres termes, on peut dire qu'une faible valeur de gamma ne prend en compte que les points proches dans le calcul de la ligne de séparation, tandis qu'une valeur de gamma prend en compte tous les points de données dans le calcul de la ligne de séparation.

Avantages

Les classificateurs SVM offrent une bonne précision et effectuent des prédictions plus rapides que l'algorithme Naïve Bayes. Ils utilisent également moins de mémoire car ils utilisent un sous-ensemble de points d'apprentissage dans la phase de décision. Le SVM fonctionne bien avec une marge de séparation claire et un espace de grande dimension.

Inconvénients

Le SVM n'est pas adapté aux grands ensembles de données en raison de son temps d'apprentissage élevé et il prend également plus de temps à l'apprentissage que Naïve Bayes. Il fonctionne mal avec les classes qui se chevauchent et est également sensible au type de noyau utilisé.

Conclusion

Félicitations, vous avez atteint la fin de ce tutoriel !

Dans ce tutoriel, vous avez abordé de nombreux aspects de l'algorithme Support vector machine, son fonctionnement, les noyaux, le réglage des hyperparamètres, la construction d'un modèle et l'évaluation d'un ensemble de données sur le cancer du sein à l'aide du paquet Scikit-learn. Vous avez également abordé ses avantages et ses inconvénients. J'espère que vous avez appris quelque chose de précieux !

Pour en savoir plus sur ce type de classificateurs, nous vous conseillons de consulter notre cours Classificateurs linéaires en Python. Il présente d'autres types de fonctions de régression et de perte, ainsi que les machines à vecteurs de support.

J'attends avec impatience vos commentaires et vos questions. Vous pouvez poser la question en laissant un commentaire et je ferai de mon mieux pour y répondre.