Pas à pas aléatoire : Explorer le modèle de la marche aléatoire

Lors de mon premier cours de statistiques basé sur le codage à l'université, mon professeur m'a posé une question : comment modéliser le mouvement brownien d'une seule particule de pollen dans une coupelle d'eau ? Après plusieurs tentatives malencontreuses, mes camarades de classe et moi-même avons fini par trouver la bonne réponse : une marche aléatoire. J'ai appris par la suite que ce modèle simple est utilisé pour modéliser toutes sortes de choses, des mouvements d'animaux aux fluctuations des cours boursiers.

Dans cet article, nous allons explorer les fondements mathématiques des marches aléatoires, examiner les différents types de marches et discuter de leurs applications. L'intérêt de la marche aléatoire réside en partie dans le fait qu'elle est utilisée dans un grand nombre de disciplines différentes. Outre mon exemple, en physique, elle permet de décrire le mouvement des particules ; en finance, elle modélise les fluctuations des cours boursiers ; et en biologie, elle explique les schémas de déplacement des animaux. Les marches aléatoires capturent le caractère aléatoire du monde réel, ce qui est essentiel pour simuler des processus stochastiques.

Pour ceux qui souhaitent acquérir des bases solides dans les statistiques qui sous-tendent la théorie de la marche aléatoire, nous vous recommandons de commencer par le cours Introduction aux statistiques en R ou le cours Introduction aux statistiques en Python.

Que sont les marches aléatoires ?

En théorie des probabilités, une marche aléatoire est un modèle décrivant une séquence d'étapes aléatoires constituant un chemin. Ou encore, nous pourrions dire qu'une marche aléatoire est un modèle mathématique qui décrit un chemin formé par une séquence d'étapes, chacune déterminée indépendamment et avec une certaine probabilité. Cette stochasticité rend les marches aléatoires intrinsèquement imprévisibles.

Imaginez une personne qui fait un pas dans une direction aléatoire à chaque instant. Au fil du temps, leur chemin forme un sentier imprévisible et sinueux. Malgré sa simplicité, ce concept a une profondeur et une polyvalence surprenantes, modélisant divers scénarios du monde réel qui impliquent le hasard.

Une explication conceptuelle de la marche aléatoire. Avec l'aimable autorisation de napkin.ai.

L'idée des marches aléatoires remonte aux premières études de probabilité. L'un des premiers exemples, souvent appelé la marche de l'ivrogne, illustre le fait qu'une personne marchant au hasard errera de manière erratique plutôt que de se diriger de manière prévisible vers une destination. Ce caractère aléatoire, associé à l'hypothèse selon laquelle chaque étape est indépendante des précédentes, a jeté les bases des modèles modernes de marche aléatoire.

Comprendre les mathématiques des marches aléatoires

Pour comprendre les marches aléatoires, commençons par un cas simple : une marche aléatoire unidimensionnelle (1D). Imaginez une particule sur une droite numérique. Il est capable de se déplacer de +1 ou de -1 sur la ligne des nombres à chaque pas. Chaque mouvement est déterminé par une probabilité égale de faire un pas vers la droite ou vers la gauche. Au fil du temps, la position de la particule forme une distribution de probabilité qui s'étend, représentant la probabilité de la trouver à différents endroits.

Ce principe peut être étendu à deux ou trois dimensions. Dans une marche aléatoire bidimensionnelle (2D), la particule se déplace sur un plan et peut se déplacer dans n'importe laquelle des quatre directions cardinales (haut, bas, gauche, droite) avec la même probabilité. De même, dans une marche aléatoire tridimensionnelle (3D), la particule se déplace dans l'espace et peut prendre l'une des six directions possibles (haut, bas, gauche, droite, avant, arrière) avec la même probabilité. Ces marches aléatoires de dimensions supérieures permettent d'appréhender des scénarios encore plus complexes et réalistes.

L'une des caractéristiques des marches aléatoires est leur nature stochastique, ce qui signifie que chaque étape ne dépend que de la position actuelle et non des étapes précédentes. Il s'agit donc d'un type de processus de Markov, un concept mathématique dans lequel l'état futur dépend uniquement de l'état présent, et non de la séquence d'événements qui l'a précédé. Ce mouvement "sans mémoire", associé à des distributions de probabilité décrivant les positions potentielles, constitue une base mathématique solide pour comprendre les marches aléatoires.

Nous pouvons analyser une marche aléatoire à l'aide de propriétés statistiques pour comprendre son comportement dans le temps. Il s'agit d'examiner des aspects tels que la distance prévue par rapport au point de départ, la distribution de probabilité des positions possibles et la probabilité de retour au point d'origine. Ces analyses nous aident à quantifier le hasard et la prévisibilité, à comprendre les schémas et à faire des prédictions.

Propriétés clés des marches aléatoires

Les marches aléatoires ont plusieurs propriétés importantes qui nous aident à comprendre leur comportement et leurs applications. Voici quelques aspects clés à prendre en considération :

Espérance et variance

Dans le cas d'une marche aléatoire unidimensionnelle, nous pouvons calculer la distance attendue (ou la position moyenne) par rapport au point de départ au fil du temps. Si chaque pas a une probabilité égale de se déplacer vers la gauche ou vers la droite, la position attendue après de nombreux pas reste nulle, ce qui signifie qu'en moyenne, le marcheur reste près de son point de départ.

Cependant, la variance de la position, qui mesure l'étendue ou la dispersion des positions possibles, augmente à chaque étape. Plus précisément, dans une marche aléatoire symétrique, la variance croît linéairement avec le nombre de pas, ce qui en fait un indicateur utile de la distance typique par rapport à l'origine au fil du temps.

Autocorrélation

Alors que les marches aléatoires simples ne présentent aucune corrélation entre les étapes (chaque étape est indépendante de la précédente), certains types de marches aléatoires introduisent une autocorrélation, les étapes passées pouvant influencer les étapes futures. Par exemple, dans une marche aléatoire biaisée, les pas peuvent avoir une légère tendance dans une direction, ce qui rend les positions plus prévisibles.

L'autocorrélation dans une marche aléatoire a un impact sur la façon dont nous modélisons et prévoyons la progression de la marche. Ceci est particulièrement pertinent dans les applications où le comportement passé influence les étapes futures, comme dans certains modèles financiers.

Théorème de la limite centrale

Le théorème de la limite centrale (CLT) indique que la somme d'un grand nombre de variables aléatoires indépendantes tend à suivre une distribution normale (ou gaussienne), quelle que soit la distribution d'origine. Dans le contexte des marches aléatoires, cela signifie qu'à mesure que le nombre de pas augmente, la distribution des positions tend à ressembler à une distribution normale. Cette propriété est utile car elle nous permet d'estimer la probabilité de trouver le marcheur à certaines distances du point de départ.

Loi des grands nombres

La loi des grands nombres (LLN) explique qu'à mesure que le nombre d'essais ou d'étapes augmente, la moyenne des résultats converge vers la vraie moyenne. Pour les marches aléatoires, cela signifie que si la position moyenne reste nulle, la variance et l'éventail des positions possibles augmentent de manière prévisible à chaque pas supplémentaire. Ce principe permet de combler le fossé entre le hasard pur et les modèles statistiques prévisibles dans de grands échantillons.

Types de marches aléatoires

Les marches aléatoires varient considérablement en fonction des règles régissant chaque étape. Ces types influencent le comportement de la marche. Certains sont conçus pour des environnements simples ou structurés, tandis que d'autres sont équipés pour des phénomènes plus complexes et plus réels. Examinons quelques-uns des types de marches aléatoires les plus courants.

Marches aléatoires 1D, 2D et 3D

La dimensionnalité d'une marche aléatoire joue un rôle fondamental dans son comportement. Dans une marche aléatoire 1D, chaque pas est soit un déplacement vers l'avant, soit un déplacement vers l'arrière le long d'une ligne. La marche est donc relativement facile à modéliser et à prévoir.

Cependant, lorsque nous passons à des marches en 2D (plan) et en 3D (espace), les chemins possibles augmentent de manière significative, introduisant de nouveaux comportements. Par exemple, dans une marche aléatoire en 2D, la probabilité de revenir au point de départ reste élevée, alors que dans une marche aléatoire en 3D, cette probabilité diminue.

Ce changement est important dans des domaines tels que la physique et la chimie, où les particules peuvent se diffuser différemment en fonction des contraintes dimensionnelles.

Marche aléatoire en treillis

Dans une marche aléatoire sur treillis, les mouvements sont limités à des points discrets d'une grille ou d'un treillis. Ce type de marche est couramment utilisé en physique et en théorie des réseaux, où les nœuds sont disposés en grille et où les déplacements ne peuvent se faire que vers les nœuds voisins.

Un exemple courant est un treillis 2D, où chaque étape permet de se déplacer vers des points adjacents sur une grille cartésienne. Cette contrainte simplifie la modélisation en limitant les trajectoires de déplacement, ce qui est utile pour simuler des réseaux complexes ou des structures moléculaires.

Marche aléatoire gaussienne

Dans une marche aléatoire gaussienne, la taille de chaque pas est déterminée par une distribution gaussienne (ou normale). Au lieu de se déplacer sur une distance fixe, la taille des pas varie selon une distribution en forme de cloche, la plupart des pas étant petits et des sauts occasionnels plus importants. Ce type de marche est fréquemment utilisé dans la modélisation financière pour tenir compte de la variabilité des variations du prix des actifs.

Marches aléatoires hétérogènes et biaisées

Les marches aléatoires hétérogènes et biaisées permettent de varier la direction et la taille des pas en fonction de certaines probabilités. Cette flexibilité les rend plus adaptables aux scénarios du monde réel.

Dans une marche aléatoire hétérogène, la probabilité de se déplacer dans n'importe quelle direction peut changer en fonction du lieu ou des conditions extérieures. Par exemple, les animaux à la recherche de nourriture peuvent privilégier les zones dont les ressources sont connues, créant ainsi une marche aléatoire biaisée. Ces promenades sont utiles pour étudier les comportements qui dépendent de facteurs contextuels.

Marche aléatoire avec dérive

Dans une marche aléatoire avec dérive, il y a une tendance constante à se déplacer dans une direction. Par exemple, les prix des actions peuvent afficher une tendance générale à la hausse au fil du temps, malgré les fluctuations quotidiennes. La dérive dans ces marches représente une force ou une tendance externe influençant la trajectoire. Ce type de modèle est souvent utilisé en finance, où les modèles intègrent un terme de dérive pour représenter la croissance ou le déclin, ce qui permet une approche plus réaliste de la prévision des prix des actifs et des tendances du marché.

Chacun de ces types de marche aléatoire a un objectif unique, offrant différentes manières de modéliser un comportement aléatoire, mais structuré. Les contraintes dimensionnelles, la distribution des étapes et la présence d'une dérive ou d'un biais rendent les marches aléatoires très polyvalentes pour la modélisation et la simulation des données dans tous les domaines.

Applications concrètes des marches aléatoires

Les marches aléatoires sont plus que de simples constructions théoriques ; elles jouent un rôle essentiel dans de nombreuses applications pratiques dans toutes les disciplines. Voyons comment les marches aléatoires permettent de résoudre des problèmes concrets dans tous les secteurs.

Applications dans le domaine de la science des données et de l'apprentissage automatique

Informatique

Les marches aléatoires sont à la base de plusieurs algorithmes informatiques, tels que l'échantillonnage aléatoire, la traversée de graphes sur le web et la segmentation d'images. Par exemple, l 'algorithme PageRank de Google utilise des marches aléatoires pour classer les pages web en fonction de leur pertinence, en simulant la façon dont un utilisateur pourrait naviguer au hasard entre les liens sur l'internet.

Extraction des caractéristiques

Dans l'apprentissage automatique, les marches aléatoires peuvent aider à extraire des caractéristiques en mettant en évidence les relations entre les points de données. Par exemple, dans l'analyse des réseaux, les marches aléatoires peuvent révéler des grappes ou des communautés, ce qui facilite les tâches telles que les systèmes de recommandation et l'analyse des réseaux sociaux.

Détection des anomalies

Les marches aléatoires peuvent également être utilisées pour détecter des anomalies dans des ensembles de données. Par exemple, si des points de données s'écartent de manière significative d'une trajectoire typique dans un modèle de marche aléatoire, ces points peuvent indiquer des événements inhabituels ou des erreurs dans les données. La détection des anomalies est particulièrement utile dans des domaines tels que la cybersécurité et la détection des fraudes.

Simulation de processus stochastiques

Les marches aléatoires simulent des processus stochastiques, ou déterminés de manière aléatoire, permettant aux scientifiques des données de modéliser des phénomènes imprévisibles du monde réel. En simulant des marches aléatoires, nous pouvons mieux comprendre les systèmes pour lesquels il est difficile de faire des prévisions précises, comme les modèles météorologiques ou le comportement des clients.

Prévision des séries temporelles

Dans l'analyse des séries temporelles, les marches aléatoires constituent la base de certains modèles de prévision, notamment l'hypothèse de la marche aléatoire en finance. Ces modèles supposent que les valeurs futures d'une série temporelle dépendent uniquement de la valeur la plus récente, sans corrélation avec les tendances passées. Pour en savoir plus sur la prévision des séries temporelles, consultez ARIMA for Time Series Forecasting : Un guide complet. Suivez également notre cours Forecasting in R avec le professeur Hyndman, qui fait le lien entre les modèles de marche aléatoire et les méthodes de prévision naïves et naïves saisonnières.

Applications dans d'autres domaines

Finances

L'une des utilisations les plus notables des marches aléatoires est la modélisation financière, en particulier pour prédire le cours des actions. L'hypothèse du marché efficient suggère que les mouvements des prix des actions sont essentiellement aléatoires, car les nouvelles informations sont instantanément absorbées, ce qui rend les prix futurs imprévisibles. Les marches aléatoires peuvent être utilisées pour modéliser les variations des cours des actions au fil du temps, illustrant la façon dont les prix fluctuent sans trajectoire prévisible.

Mathématiques

En mathématiques pures, les marches aléatoires permettent de résoudre des problèmes complexes. Par exemple, ils sont utiles pour résoudre l'équation de Laplace, analyser les réseaux et explorer la combinatoire.

Physique et chimie

Dans les sciences physiques, les marches aléatoires sont essentielles pour modéliser les processus de diffusion, tels que la façon dont les molécules se propagent dans un milieu. Le mouvement brownien, où des particules en suspension dans un fluide se déplacent de manière imprévisible en raison de collisions avec les molécules environnantes, est un exemple classique qui peut être simulé avec précision à l'aide de marches aléatoires. C'est d'ailleurs ainsi que j'ai découvert les marches aléatoires.

Biologie

Les marches aléatoires sont très utiles en écologie pour étudier les schémas de déplacement des animaux. Les animaux à la recherche de ressources peuvent sembler se déplacer au hasard, parfois en privilégiant les régions où les ressources sont connues. D'autres concepts biologiques, tels que la propagation des populations ou des gènes, peuvent souvent être modélisés à l'aide des principes de la marche aléatoire, ce qui facilite la compréhension et la prévision des changements au sein des écosystèmes.

Cas particuliers et variantes des marches aléatoires

Outre la marche aléatoire classique, plusieurs variantes avancées étendent le concept pour l'adapter à des applications spécialisées.

Marches d'évitement

Une marche auto-évitante est une marche aléatoire dans laquelle le chemin ne revient pas sur une position qu'il a déjà dépassée. Cette variante est particulièrement utile dans des domaines tels que la chimie des polymères, où elle permet de modéliser la formation des chaînes de polymères sans qu'elles se croisent. Comme chaque étape évite les points visités précédemment, les marches auto-évitantes sont plus contraignantes que les marches aléatoires traditionnelles. Cela signifie qu'ils sont difficiles à calculer, mais qu'ils sont utiles pour comprendre les chemins qui ne se chevauchent pas dans les espaces confinés.

Branchement

Dans les marches aléatoires ramifiées, le chemin peut se diviser en plusieurs branches, chaque branche suivant une marche aléatoire. Ce type de marche est essentiel pour modéliser les processus de ramification tels que la division cellulaire ou la diffusion d'informations dans les réseaux. Chaque "branche" représente un chemin aléatoire indépendant qui provient d'une source commune.

Marches corrélées

Les marches corrélées poussent ce concept un peu plus loin, la direction de chaque étape étant partiellement influencée par l'étape précédente. Cette variante est utile pour modéliser l'inertie dans les systèmes où les changements se produisent progressivement plutôt qu'aléatoirement. Les marches corrélées sont souvent utilisées en finance pour simuler les tendances des prix ou en écologie du mouvement pour comprendre comment les animaux naviguent dans leur environnement en se souvenant de leur direction passée.

Marches en boucle

Une marche en boucle est une variante où les boucles, ou les chemins qui se croisent, sont supprimées au fur et à mesure qu'elles se forment. Chaque fois qu'une étape revient sur une position, la boucle intermédiaire est effacée, laissant un chemin rationalisé et non répétitif. Les marches en boucle sont couramment utilisées dans les algorithmes d'analyse de réseaux et de génération de labyrinthes, car elles créent des chemins qui évitent la redondance.

Implémentation de marches aléatoires en Python

Essayons d'implémenter une marche aléatoire en Python. Pour commencer, assurez-vous que Python est installé (nous utiliserons Python 3.10) et que les bibliothèques nécessaires sont disponibles. Vous pouvez installer les bibliothèques manquantes à l'aide de pip. Voici ce que nous allons utiliser :

import numpy as np # for numerical operations and generating random steps
import matplotlib.pyplot as plt # for plotting and visualizing the random walks

Marche aléatoire 1D

Nous commencerons par une simple marche aléatoire unidimensionnelle, où chaque pas est soit +1, soit -1, choisi au hasard.

# Parameters
n_steps = 100  # Number of steps

# Generate random steps: +1 or -1
steps = np.random.choice([-1, 1], size=n_steps)

# Calculate positions
positions = np.cumsum(steps)

# Plot the random walk
plt.figure(figsize=(10, 6))
plt.plot(positions, marker='o', linestyle='-', markersize=4)
plt.title("1D Random Walk")
plt.xlabel("Step")
plt.ylabel("Position")
plt.grid(True)
plt.show()

Cela génère une simple marche aléatoire et permet de visualiser la progression dans le temps. Voici le résultat lorsque j'exécute ce code :

N'oubliez pas que nous utilisons un modèle stochastique. Cela signifie qu'à chaque fois que nous l'exécutons, le résultat sera légèrement différent.

Marche aléatoire en 2D

Étendons maintenant la marche aléatoire à deux dimensions. À chaque étape, la direction est choisie de manière aléatoire.

# Parameters
n_steps = 500

# Generate random steps in x and y directions
x_steps = np.random.choice([-1, 1], size=n_steps)
y_steps = np.random.choice([-1, 1], size=n_steps)

# Calculate positions
x_positions = np.cumsum(x_steps)
y_positions = np.cumsum(y_steps)

# Plot the 2D random walk
plt.figure(figsize=(8, 8))
plt.plot(x_positions, y_positions, marker='o', linestyle='-', markersize=2, label='Random Walk')
plt.plot(x_positions[0], y_positions[0], 'ro', markersize=8, label='Start')  # Red dot for start
plt.plot(x_positions[-1], y_positions[-1], 'ko', markersize=8, label='End')  # Black dot for end
plt.title("2D Random Walk")
plt.xlabel("X Position")
plt.ylabel("Y Position")
plt.grid(True)
plt.axis('equal')  # Ensures equal scaling for both axes
plt.legend()
plt.show()

Ce code crée un chemin visuellement attrayant en deux dimensions.

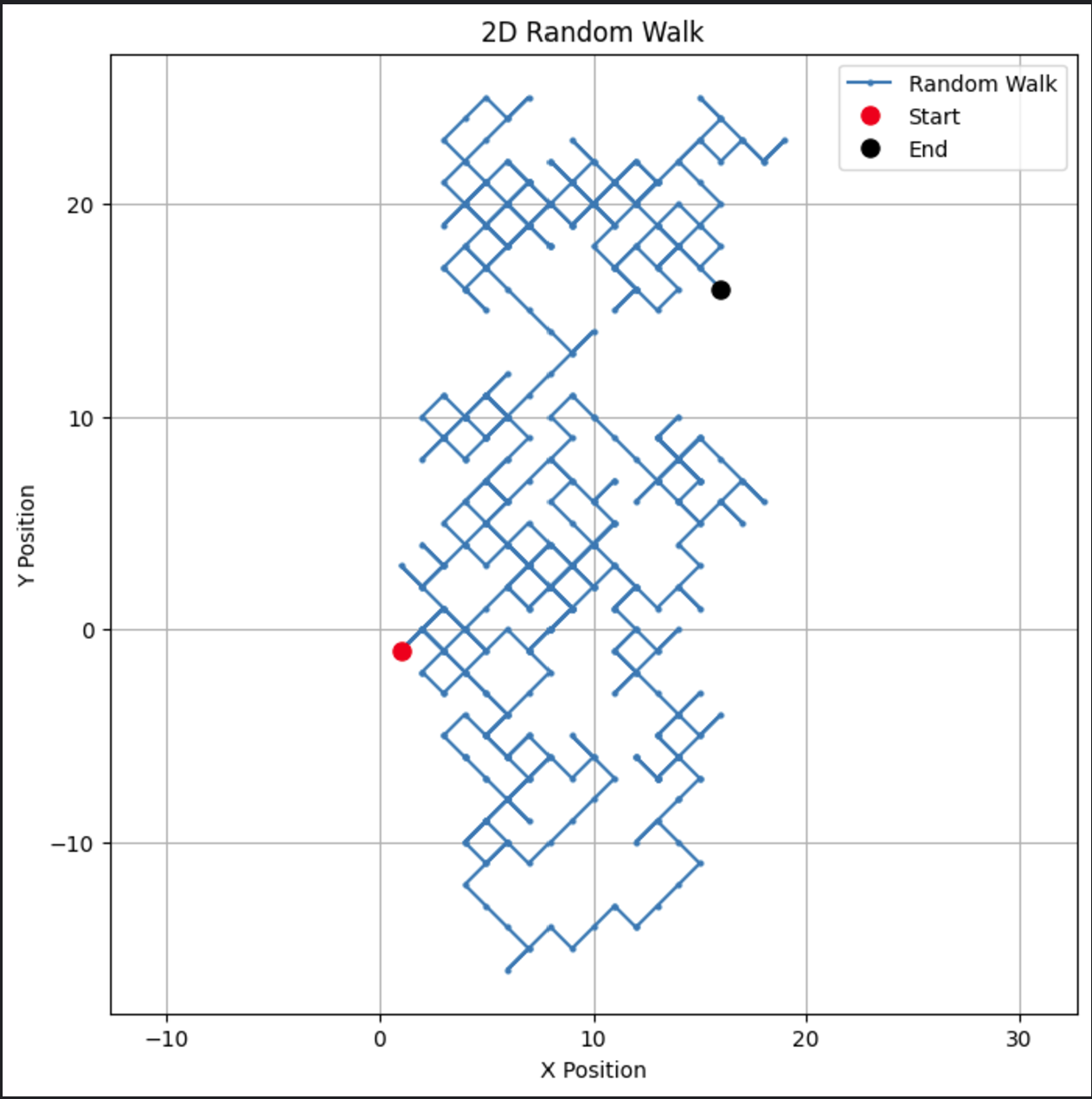
Ce type de marche aléatoire bidimensionnelle pourrait être modifié pour s'adapter à des applications telles que le mouvement des particules ou la modélisation spatiale.

Marche aléatoire biaisée

Enfin, prenons un exemple un peu plus complexe : une marche aléatoire biaisée. Pour introduire un biais, nous pouvons ajuster les probabilités de chaque direction de pas. Par exemple, nous pourrions faire en sorte que les démarches ascendantes soient plus probables.

# Parameters
n_steps = 100
bias = 0.7  # Probability of stepping +1

# Generate biased random steps in x and y directions
x_steps = np.random.choice([-1, 1], size=n_steps, p=[1-bias, bias])
y_steps = np.random.choice([-1, 1], size=n_steps, p=[1-bias, bias])

# Calculate positions
x_positions = np.cumsum(x_steps)
y_positions = np.cumsum(y_steps)

# Plot the biased 2D random walk
plt.figure(figsize=(8, 8))
plt.plot(x_positions, y_positions, marker='o', linestyle='-', markersize=2, label='Random Walk')
plt.plot(x_positions[0], y_positions[0], 'ro', markersize=8, label='Start')  # Red dot for start
plt.plot(x_positions[-1], y_positions[-1], 'ko', markersize=8, label='End')  # Black dot for end
plt.title("Biased 2D Random Walk")
plt.xlabel("X Position")
plt.ylabel("Y Position")
plt.grid(True)
plt.axis('equal')  # Ensures equal scaling for both axes
plt.legend()
plt.show()

En modifiant le biais, vous pouvez observer comment la marche tend à favoriser une direction particulière, simulant ainsi des scénarios réels tels que la dérive des cours boursiers ou les schémas de migration des animaux.

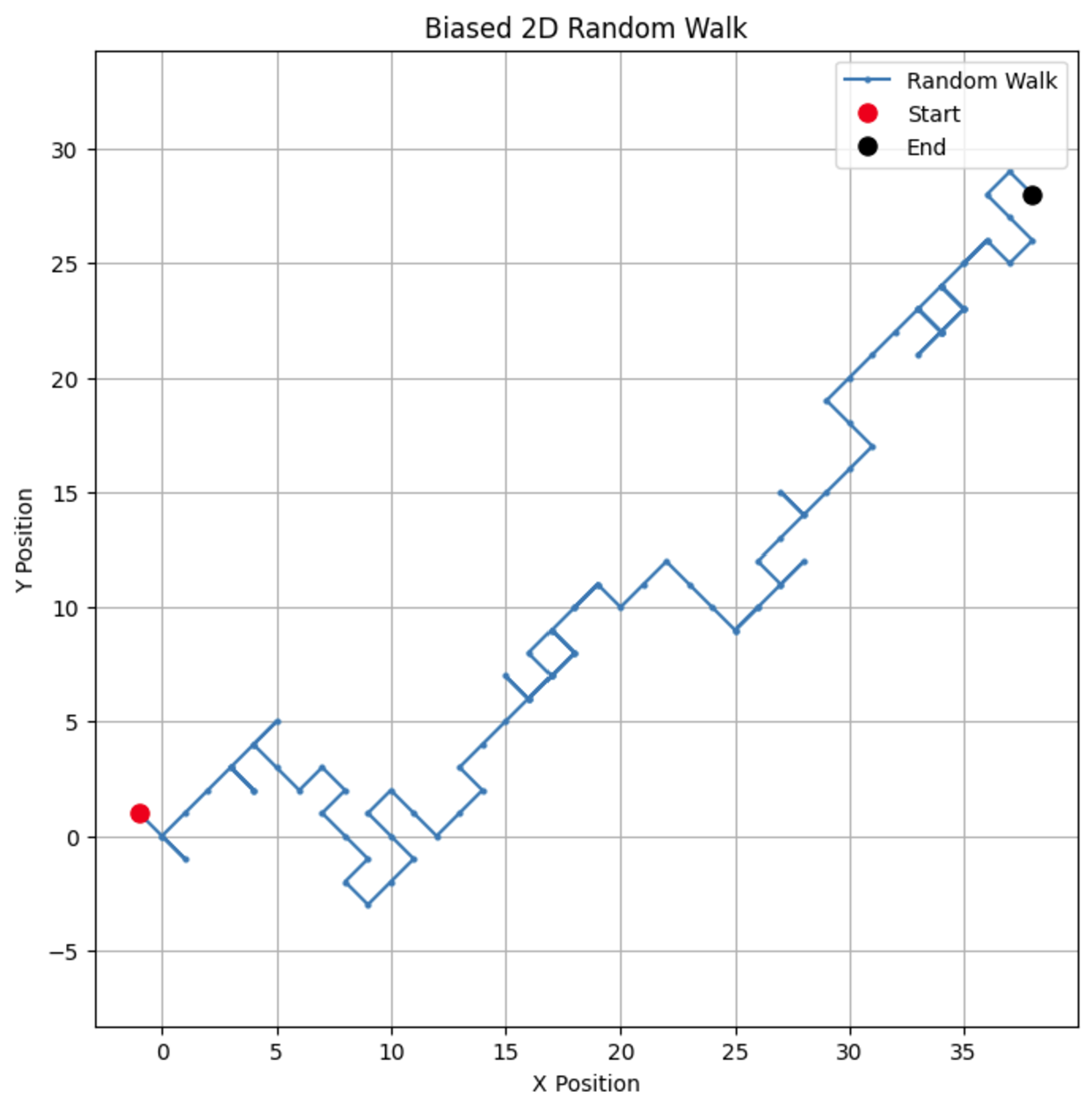
Si nous modifions le paramètre de biais à 0,55, nous constatons une différence spectaculaire dans la manière dont le modèle se comporte. Bien qu'il y ait toujours une tendance à la hausse, celle-ci n'est pas aussi forte, ce qui entraîne davantage de boucles et de détours.

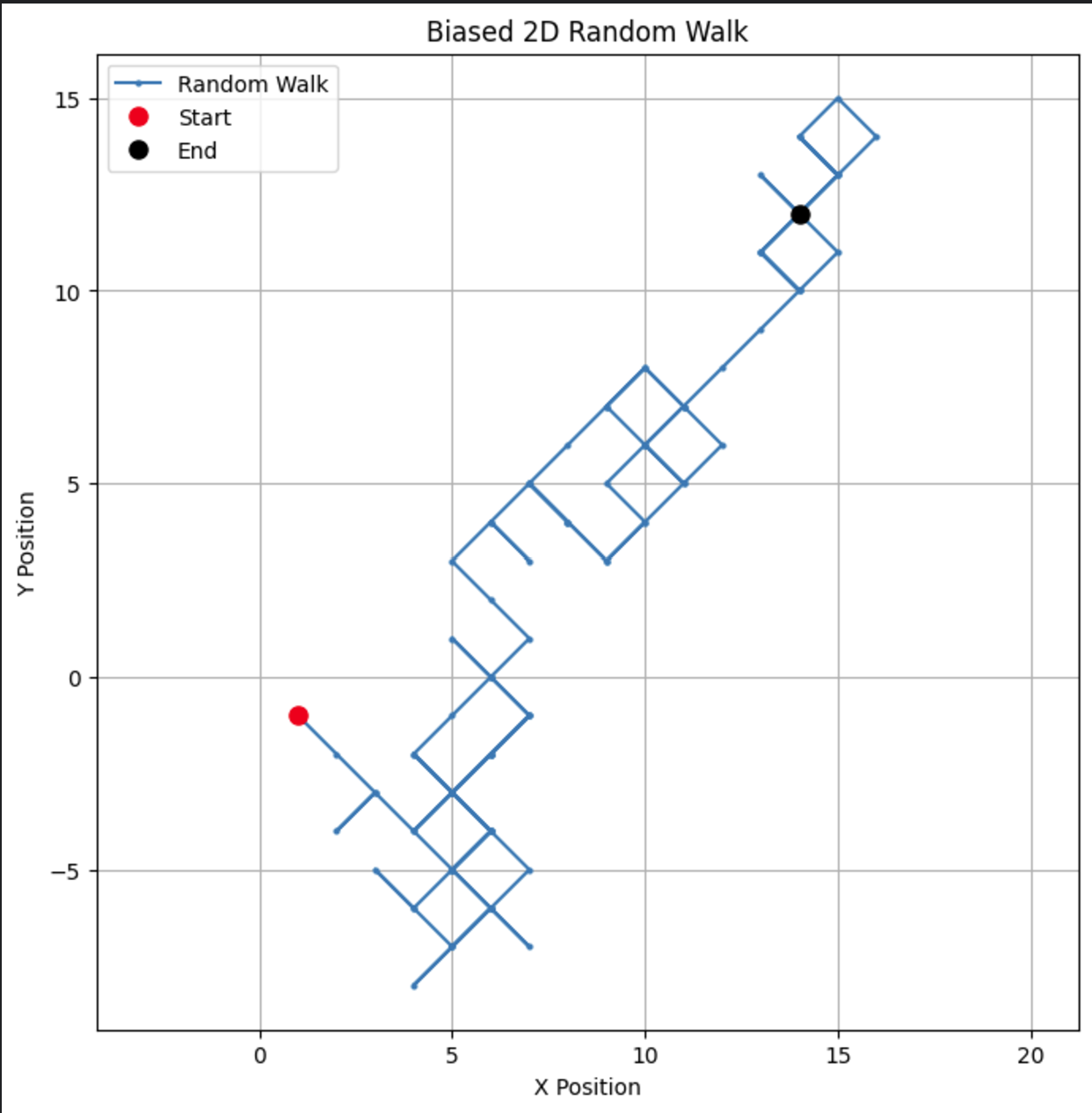
Conclusion

Les marches aléatoires sont un outil de modélisation précieux pour les scientifiques des données, applicable dans des domaines allant de la physique à la finance et au-delà. Leur capacité à modéliser des processus complexes et stochastiques les rend indispensables dans de nombreux scénarios du monde réel.

Vous en voulez encore ? Consultez la suite de cours de probabilités et de statistiques de DataCamp. Vous trouverez toutes sortes d'excellents cours en Python et en R. Si vous êtes intéressé par un contenu plus avancé, consultez le cours de DataCamp sur la simulation statistique en Python et le tutoriel Introduction à l'apprentissage automatique. Ou si vous êtes prêt à tester vos connaissances, attaquez-vous à ces énigmes sur les probabilités.