Step by Random Step: Erkundung des Random Walk Modells

In meinem ersten kodierungsbasierten Statistikkurs an der Uni schlug mein Lehrer eine Frage vor: Wie können wir die Brownsche Bewegung eines einzelnen Pollenteilchens in einer Schale mit Wasser modellieren? Nach mehreren fehlgeleiteten Versuchen kamen meine Mitschüler und ich schließlich auf die richtige Antwort: ein Random Walk. Später erfuhr ich, dass dieses einfache Modell verwendet wird, um alle möglichen Dinge zu modellieren, von Tierbewegungen bis hin zu Aktienkursschwankungen.

In diesem Artikel werden wir die mathematischen Grundlagen von Random Walks erkunden, verschiedene Typen untersuchen und ihre Anwendungen diskutieren. Ein Teil dessen, was den Random Walk so interessant macht, ist, dass er in so vielen verschiedenen Disziplinen verwendet wird. Neben meinem Beispiel hilft sie in der Physik, die Bewegung von Teilchen zu beschreiben, in der Finanzwelt modelliert sie Aktienkursschwankungen und in der Biologie erklärt sie die Bewegungsmuster von Tieren. Random Walks bilden die Zufälligkeit der realen Welt ab, die für die Simulation stochastischer Prozesse entscheidend ist.

Für diejenigen, die eine solide Grundlage in der Statistik, die der Random-Walk-Theorie zugrunde liegt, aufbauen wollen, empfehlen wir, mit dem Kurs Einführung in die Statistik in R oder dem Kurs Einführung in die Statistik in Python zu beginnen.

Was sind zufällige Spaziergänge?

In der Wahrscheinlichkeitstheorie ist ein Random Walk ein Modell, das eine Folge von zufälligen Schritten beschreibt, die einen Pfad bilden. Oder wir könnten sagen, dass ein Random Walk ein mathematisches Modell ist, das einen Weg beschreibt, der durch eine Abfolge von Schritten gebildet wird, die jeweils unabhängig und mit einer bestimmten Wahrscheinlichkeit bestimmt werden. Diese Stochastik macht Random Walks von Natur aus unberechenbar.

Stell dir vor, eine Person macht in jedem Moment einen Schritt in eine zufällige Richtung. Mit der Zeit wird ihr Weg zu einer unvorhersehbaren, gewundenen Spur. Trotz seiner Einfachheit hat dieses Konzept eine überraschende Tiefe und Vielseitigkeit, da es verschiedene reale Szenarien modelliert, bei denen der Zufall eine Rolle spielt.

Eine konzeptionelle Erklärung des Random Walk. Bild mit freundlicher Genehmigung von napkin.ai.

Die Idee der Random Walks geht auf die frühe Wahrscheinlichkeitsforschung zurück. Eines der frühesten Beispiele, das oft als "Trunkenheitsgang" bezeichnet wird, zeigt, wie eine Person, die wahllos tritt, unberechenbar umherwandert, anstatt sich vorhersehbar auf ein Ziel zuzubewegen. Diese Zufälligkeit, kombiniert mit der Annahme, dass jeder Schritt unabhängig von den vorherigen ist, legte den Grundstein für moderne Random-Walk-Modelle.

Die Mathematik von Random Walks verstehen

Um Random Walks zu verstehen, wollen wir mit einem einfachen Fall beginnen: einem eindimensionalen (1D) Random Walk. Stell dir ein Teilchen auf einer Zahlenlinie vor. Er kann sich bei jedem Schritt entweder +1 oder -1 entlang der Zahlenreihe bewegen. Jeder Zug wird durch eine gleiche Wahrscheinlichkeit bestimmt, nach rechts oder links zu gehen. Im Laufe der Zeit bildet die Position des Teilchens eine Wahrscheinlichkeitsverteilung, die sich ausbreitet und die Wahrscheinlichkeit darstellt, es an verschiedenen Orten zu finden.

Dieses Prinzip kann auf zwei oder drei Dimensionen erweitert werden. Bei einem zweidimensionalen (2D) Random Walk bewegt sich das Teilchen auf einer Ebene und kann mit gleicher Wahrscheinlichkeit in jede der vier Himmelsrichtungen (oben, unten, links, rechts) gehen. In ähnlicher Weise bewegt sich das Teilchen bei einem dreidimensionalen (3D) Random Walk im Raum und kann mit gleicher Wahrscheinlichkeit in jede der sechs möglichen Richtungen (auf, ab, links, rechts, vorwärts, rückwärts) gehen. Diese höherdimensionalen Random Walks erfassen noch komplexere und realistischere Szenarien.

Ein entscheidendes Merkmal von Random Walks ist ihre stochastische Natur, d.h. jeder Schritt hängt nur von der aktuellen Position und nicht von den vorherigen Schritten ab. Das macht sie zu einer Art Markov-Prozess - ein mathematisches Konzept, bei dem der zukünftige Zustand nur vom aktuellen Zustand abhängt und nicht von der Abfolge der Ereignisse, die ihm vorausgegangen sind. Diese "gedächtnislose" Bewegung, kombiniert mit Wahrscheinlichkeitsverteilungen, die mögliche Positionen beschreiben, bietet eine solide mathematische Grundlage für das Verständnis von Random Walks.

Wir können einen Random Walk anhand statistischer Eigenschaften analysieren, um sein Verhalten im Laufe der Zeit zu verstehen. Dabei werden Aspekte wie die erwartete Entfernung vom Startpunkt, die Wahrscheinlichkeitsverteilung möglicher Positionen und die Wahrscheinlichkeit der Rückkehr zum Ursprung untersucht. Diese Analysen helfen uns, Zufälligkeit und Vorhersehbarkeit zu quantifizieren, Muster zu erkennen und Vorhersagen zu treffen.

Wichtige Eigenschaften von Random Walks

Random Walks haben mehrere wichtige Eigenschaften, die uns helfen, ihr Verhalten und ihre Anwendungen zu verstehen. Hier sind einige wichtige Aspekte, die du beachten solltest:

Erwartung und Varianz

Bei einem eindimensionalen Random Walk können wir die erwartete Entfernung (oder mittlere Position) vom Startpunkt über die Zeit berechnen. Wenn jeder Schritt die gleiche Wahrscheinlichkeit hat, sich nach links oder rechts zu bewegen, bleibt die erwartete Position nach vielen Schritten gleich Null, was bedeutet, dass der Wanderer im Durchschnitt in der Nähe des Startpunkts bleibt.

Die Varianz der Position, die die Streuung der möglichen Positionen misst, steigt jedoch mit jedem Schritt. Bei einem symmetrischen Random Walk wächst die Varianz linear mit der Anzahl der Schritte, was sie zu einem nützlichen Indikator für die typische Entfernung vom Ursprung über die Zeit macht.

Autokorrelation

Während einfache Random Walks keine Korrelation zwischen den Schritten aufweisen (jeder Schritt ist unabhängig vom letzten), gibt es bei bestimmten Arten von Random Walks eine Autokorrelation, bei der vergangene Schritte die zukünftigen beeinflussen können. Bei einem voreingenommenen Random Walk können die Schritte zum Beispiel eine leichte Tendenz in eine Richtung haben, wodurch die Positionen besser vorhersehbar sind.

Die Autokorrelation in einem Random Walk hat Auswirkungen darauf, wie wir den Verlauf des Walks modellieren und vorhersagen. Das ist besonders wichtig für Anwendungen, bei denen das Verhalten in der Vergangenheit zukünftige Schritte beeinflusst, wie z.B. bei bestimmten Finanzmodellen.

Zentrales Grenzwertsatztheorem

Der zentrale Grenzwertsatz (CLT) besagt, dass die Summe einer großen Anzahl unabhängiger Zufallsvariablen dazu neigt, einer Normalverteilung (oder Gaußverteilung) zu folgen, unabhängig von der ursprünglichen Verteilung. Im Zusammenhang mit Random Walks bedeutet das, dass die Verteilung der Positionen mit zunehmender Schrittzahl eher einer Normalverteilung ähnelt. Das ist eine nützliche Eigenschaft, denn sie ermöglicht es uns, die Wahrscheinlichkeit, den Wanderer in bestimmten Entfernungen vom Startpunkt zu finden, zu schätzen.

Gesetz der großen Zahlen

Das Gesetz der großen Zahlen (Law of Large Numbers, LLN ) besagt, dass sich der Durchschnitt der Ergebnisse mit zunehmender Anzahl von Versuchen oder Schritten dem wahren Durchschnitt annähert. Für Random Walks bedeutet das, dass die durchschnittliche Position zwar gleich Null bleibt, die Varianz und die Bandbreite der möglichen Positionen aber mit jedem weiteren Schritt vorhersehbar zunehmen. Dieses Prinzip hilft, die Lücke zwischen reinem Zufall und vorhersehbaren statistischen Mustern in großen Stichproben zu schließen.

Arten von Random Walks

Random Walks sind sehr unterschiedlich, je nachdem, welche Regeln für jeden Schritt gelten. Diese Typen beeinflussen, wie sich der Weg verhält. Einige sind für einfache oder strukturierte Umgebungen konzipiert, während andere für komplexere Phänomene in der realen Welt ausgestattet sind. Sehen wir uns einige der häufigsten Arten von Random Walks an.

1D-, 2D- und 3D-Zufallswege

Die Dimensionalität eines Random Walk spielt eine grundlegende Rolle für sein Verhalten. Bei einem 1D Random Walk ist jeder Schritt entweder ein Vorwärts- oder ein Rückwärtsgang entlang einer Linie. Das macht es relativ einfach, die Wanderung zu modellieren und vorherzusagen.

Wenn wir jedoch zu 2D- (Ebene) und 3D- (Raum) Spaziergängen übergehen, erhöhen sich die möglichen Pfade erheblich und führen zu neuen Verhaltensweisen. Bei einem 2D-Zufallsspaziergang zum Beispiel bleibt die Wahrscheinlichkeit, zum Ausgangspunkt zurückzukehren, hoch, während sie bei einem 3D-Zufallsspaziergang abnimmt.

Diese Veränderung ist in Bereichen wie der Physik und der Chemie wichtig, in denen sich Teilchen je nach Dimension unterschiedlich ausbreiten können.

Lattice Random Walk

Bei einem Lattice Random Walk beschränkt sich die Bewegung auf diskrete Punkte auf einem Netz oder Gitter. Diese Art von Spaziergang wird häufig in der Physik und der Netzwerktheorie verwendet, wo die Knoten in einem Gitter angeordnet sind und sich nur zu benachbarten Knoten bewegen können.

Ein gängiges Beispiel ist ein 2D-Gitter, bei dem jeder Schritt eine Bewegung zu benachbarten Punkten auf einem kartesischen Gitter ermöglicht. Diese Einschränkung vereinfacht die Modellierung durch die Begrenzung der Bewegungspfade, was bei der Simulation von komplexen Netzwerken oder molekularen Strukturen nützlich ist.

Gaußsche Zufallsbewegung

Bei einem Gauß'schen Random Walk wird die Größe der einzelnen Schritte durch eine Gauß'sche (oder normale) Verteilung bestimmt. Anstatt sich um eine feste Strecke zu bewegen, variiert die Schrittgröße entsprechend einer Glockenkurvenverteilung, wobei die meisten Schritte klein sind und gelegentlich größere Sprünge gemacht werden. Diese Art der Wanderung wird häufig in der Finanzmodellierung verwendet, um die Variabilität von Vermögenspreisänderungen zu berücksichtigen.

Heterogene und verzerrte Random Walks

Heterogene und voreingenommene Random Walks ermöglichen eine Variation der Schrittrichtung und -größe auf der Grundlage bestimmter Wahrscheinlichkeiten. Diese Flexibilität macht sie anpassungsfähiger an reale Szenarien.

Bei einem heterogenen Random Walk kann sich die Wahrscheinlichkeit, sich in eine bestimmte Richtung zu bewegen, je nach Standort oder äußeren Bedingungen ändern. Zum Beispiel können Tiere auf der Suche nach Nahrung Gebiete mit bekannten Ressourcen bevorzugen, was zu einer verzerrten Zufallsbewegung führt. Diese Spaziergänge sind nützlich, um Verhaltensweisen zu untersuchen, die von kontextabhängigen Faktoren abhängen.

Random Walk mit Drift

Bei einem Random Walk mit Drift gibt es eine beständige Tendenz, sich in eine Richtung zu bewegen. Zum Beispiel können die Aktienkurse trotz täglicher Schwankungen im Laufe der Zeit einen allgemeinen Aufwärtstrend aufweisen. Die Drift bei diesen Wanderungen stellt eine äußere Kraft oder einen Trend dar, der den Weg beeinflusst. Diese Art von Modellen wird häufig in der Finanzwelt verwendet, wo sie einen Drift-Term enthalten, um Wachstum oder Rückgang darzustellen und einen realistischeren Ansatz für die Vorhersage von Vermögenspreisen und Markttrends zu bieten.

Jede dieser Arten von Random Walk dient einem bestimmten Zweck und bietet verschiedene Möglichkeiten, zufälliges, aber strukturiertes Verhalten zu modellieren. Die Dimensionsbeschränkungen, die Verteilung der Schritte und das Vorhandensein von Drift oder Verzerrungen machen Random Walks sehr vielseitig für die Datenmodellierung und Simulation in verschiedenen Bereichen.

Anwendungen von Random Walks in der realen Welt

Random Walks sind mehr als nur theoretische Konstrukte; sie spielen eine wesentliche Rolle in vielen praktischen Anwendungen in allen Disziplinen. Wir wollen herausfinden, wie Random Walks bei der Lösung realer Probleme in verschiedenen Sektoren helfen.

Anwendungen in Datenwissenschaft und maschinellem Lernen

Informatik

Random Walks bilden die Grundlage für verschiedene Algorithmen in der Informatik, z. B. für Zufallsstichproben, die Durchquerung von Webgraphen und die Segmentierung von Bildern. Der PageRank-Algorithmus von Google verwendet zum Beispiel Random Walks, um Webseiten nach ihrer Relevanz zu bewerten, und simuliert so, wie ein Nutzer zufällig zwischen Links im Internet navigieren würde.

Merkmalsextraktion

Beim maschinellen Lernen können Random Walks dabei helfen, Merkmale zu extrahieren, indem sie die Beziehungen zwischen den Datenpunkten hervorheben. In der Netzwerkanalyse können Random Walks zum Beispiel Cluster oder Gemeinschaften aufdecken, was bei Aufgaben wie Empfehlungssystemen und der Analyse sozialer Netzwerke hilfreich ist.

Erkennung von Anomalien

Random Walks können auch verwendet werden, um Anomalien in Datensätzen zu erkennen. Wenn zum Beispiel Datenpunkte in einem Random-Walk-Modell erheblich von einem typischen Pfad abweichen, könnten diese Punkte auf ungewöhnliche Ereignisse oder Fehler in den Daten hinweisen. Die Erkennung von Anomalien ist besonders wertvoll in Bereichen wie Cybersicherheit und Betrugserkennung.

Stochastische Prozesse simulieren

Random Walks simulieren stochastische oder zufällige Prozesse, die es Datenwissenschaftlern ermöglichen, unvorhersehbare Phänomene der realen Welt zu modellieren. Durch die Simulation von Random Walks können wir Einblicke in Systeme gewinnen, bei denen eine genaue Vorhersage schwierig ist, wie z. B. Wettermuster oder Kundenverhalten.

Zeitreihenprognose

In der Zeitreihenanalyse bilden Random Walks die Grundlage für bestimmte Prognosemodelle, darunter die Random-Walk-Hypothese im Finanzwesen. Diese Modelle gehen davon aus, dass die zukünftigen Werte einer Zeitreihe nur vom jüngsten Wert abhängen und keine Korrelation zu vergangenen Trends aufweisen. Weitere Informationen zur Zeitreihenprognose findest du unter ARIMA for Time Series Forecasting: Ein kompletter Leitfaden. Besuche auch unseren Kurs "Forecasting in R" mit Professor Hyndman, der Random-Walk-Modelle mit naiven und saisonalen naiven Prognosemethoden verbindet.

Anwendungen in anderen Bereichen

Finanzen

Eine der bemerkenswertesten Anwendungen von Random Walks ist die Finanzmodellierung, insbesondere für die Vorhersage von Aktienkursen. Die Hypothese des effizienten Marktes besagt, dass Aktienkursbewegungen im Wesentlichen zufällig sind, da neue Informationen sofort aufgenommen werden und künftige Kurse unvorhersehbar sind. Mit Hilfe von Random Walks können Aktienkursveränderungen im Laufe der Zeit modelliert werden, um zu zeigen, wie die Preise ohne einen vorhersehbaren Pfad schwanken.

Mathematik

In der reinen Mathematik liefern Random Walks Lösungen für komplexe Probleme. Sie sind zum Beispiel nützlich, um die Laplace-Gleichung zu lösen, Netzwerke zu analysieren und die Kombinatorik zu erforschen.

Physik und Chemie

In den Naturwissenschaften sind Random Walks entscheidend für die Modellierung von Diffusionsprozessen, z. B. wie sich Moleküle in einem Medium ausbreiten. Die Brownsche Bewegung, bei der sich in einer Flüssigkeit schwebende Teilchen aufgrund von Zusammenstößen mit den umgebenden Molekülen unvorhersehbar bewegen, ist ein klassisches Beispiel, das mit Random Walks genau simuliert werden kann. So habe ich zum ersten Mal von Random Walks erfahren.

Biologie

Random Walks sind in der Ökologie nützlich, um die Bewegungsmuster von Tieren zu untersuchen. Tiere, die auf der Suche nach Ressourcen sind, können sich scheinbar zufällig bewegen, manchmal in Richtung von Regionen mit bekannten Ressourcen. Andere biologische Konzepte, wie die Ausbreitung von Populationen oder Genen, können oft mit dem Prinzip des Random Walk modelliert werden, was es einfacher macht, Veränderungen in Ökosystemen zu verstehen und vorherzusagen.

Sonderfälle und Varianten von Random Walks

Neben dem klassischen Random Walk gibt es mehrere fortgeschrittene Varianten, die das Konzept für spezielle Anwendungen erweitern.

Selbstausweichende Spaziergänge

Eine selbstausweichende Wanderung ist eine zufällige Wanderung, bei der der Pfad nicht zu einer bereits passierten Stelle zurückkehrt. Diese Variante ist besonders nützlich in Bereichen wie der Polymerchemie, wo sie modellieren kann, wie sich Polymerketten bilden, ohne sich zu kreuzen. Da jeder Schritt zuvor besuchte Punkte vermeidet, sind Self-Avoiding Walks stärker eingeschränkt als traditionelle Random Walks. Das bedeutet, dass sie eine rechnerische Herausforderung darstellen, aber nützlich sind, um nicht überlappende Pfade auf engem Raum zu verstehen.

Verzweigung

Bei verzweigten Random Walks kann sich der Pfad in mehrere Zweige aufteilen, wobei jeder Zweig einem Random Walk folgt. Diese Art von Spaziergang ist wichtig für die Modellierung von Verzweigungsprozessen wie der Zellteilung oder der Verbreitung von Informationen in Netzwerken. Jeder "Ast" stellt einen unabhängigen, zufälligen Pfad dar, der von einer gemeinsamen Quelle ausgeht.

Korrelierte Spaziergänge

Korrelierte Spaziergänge gehen noch einen Schritt weiter. Dabei wird die Richtung jedes Schritts teilweise durch den vorherigen Schritt beeinflusst. Diese Variante ist nützlich, um die Trägheit von Systemen zu modellieren, in denen Veränderungen nicht zufällig, sondern schrittweise erfolgen. Korrelierte Spaziergänge werden häufig in der Finanzwelt eingesetzt, um Preistrends zu simulieren, oder in der Bewegungsökologie, um zu verstehen, wie Tiere sich in ihrer Umgebung mit einer gewissen Erinnerung an ihre frühere Richtung bewegen.

Spaziergänge mit Schleifenlöschung

Ein schleifenloser Weg ist eine Variante, bei der Schleifen oder sich kreuzende Wege entfernt werden, sobald sie entstehen. Jedes Mal, wenn ein Schritt zu einer Position zurückkehrt, wird die dazwischen liegende Schleife gelöscht, sodass ein schlanker, sich nicht wiederholender Pfad entsteht. Spaziergänge mit Schleifen werden häufig in der Netzwerkanalyse und in Algorithmen zur Erstellung von Labyrinthen eingesetzt, da sie Pfade erstellen, die Redundanzen vermeiden.

Implementierung von Random Walks in Python

Lass uns versuchen, einen Random Walk in Python zu implementieren. Um loszulegen, musst du sicherstellen, dass du Python installiert hast (wir verwenden Python 3.10) und die notwendigen Bibliotheken verfügbar sind. Du kannst alle fehlenden Bibliotheken mit pip installieren. Das werden wir verwenden:

import numpy as np # for numerical operations and generating random steps
import matplotlib.pyplot as plt # for plotting and visualizing the random walks

1D Random Walk

Wir beginnen mit einem einfachen eindimensionalen Random Walk, bei dem jeder Schritt entweder +1 oder -1 ist und zufällig gewählt wird.

# Parameters
n_steps = 100  # Number of steps

# Generate random steps: +1 or -1
steps = np.random.choice([-1, 1], size=n_steps)

# Calculate positions
positions = np.cumsum(steps)

# Plot the random walk
plt.figure(figsize=(10, 6))
plt.plot(positions, marker='o', linestyle='-', markersize=4)
plt.title("1D Random Walk")
plt.xlabel("Step")
plt.ylabel("Position")
plt.grid(True)
plt.show()

Dies erzeugt einen einfachen Random Walk und visualisiert den Verlauf über die Zeit. Hier ist die Ausgabe, wenn ich diesen Code ausführe:

Denke daran, dass wir ein stochastisches Modell verwenden. Das bedeutet, dass die Ausgabe jedes Mal, wenn wir sie ausführen, etwas anders aussieht.

2D Random Walk

Erweitern wir nun den Random Walk auf zwei Dimensionen. Bei jedem Schritt wird die Richtung zufällig gewählt.

# Parameters
n_steps = 500

# Generate random steps in x and y directions
x_steps = np.random.choice([-1, 1], size=n_steps)
y_steps = np.random.choice([-1, 1], size=n_steps)

# Calculate positions
x_positions = np.cumsum(x_steps)
y_positions = np.cumsum(y_steps)

# Plot the 2D random walk
plt.figure(figsize=(8, 8))
plt.plot(x_positions, y_positions, marker='o', linestyle='-', markersize=2, label='Random Walk')
plt.plot(x_positions[0], y_positions[0], 'ro', markersize=8, label='Start')  # Red dot for start
plt.plot(x_positions[-1], y_positions[-1], 'ko', markersize=8, label='End')  # Black dot for end
plt.title("2D Random Walk")
plt.xlabel("X Position")
plt.ylabel("Y Position")
plt.grid(True)
plt.axis('equal')  # Ensures equal scaling for both axes
plt.legend()
plt.show()

Dieser Code erzeugt einen visuell ansprechenden Pfad in zwei Dimensionen.

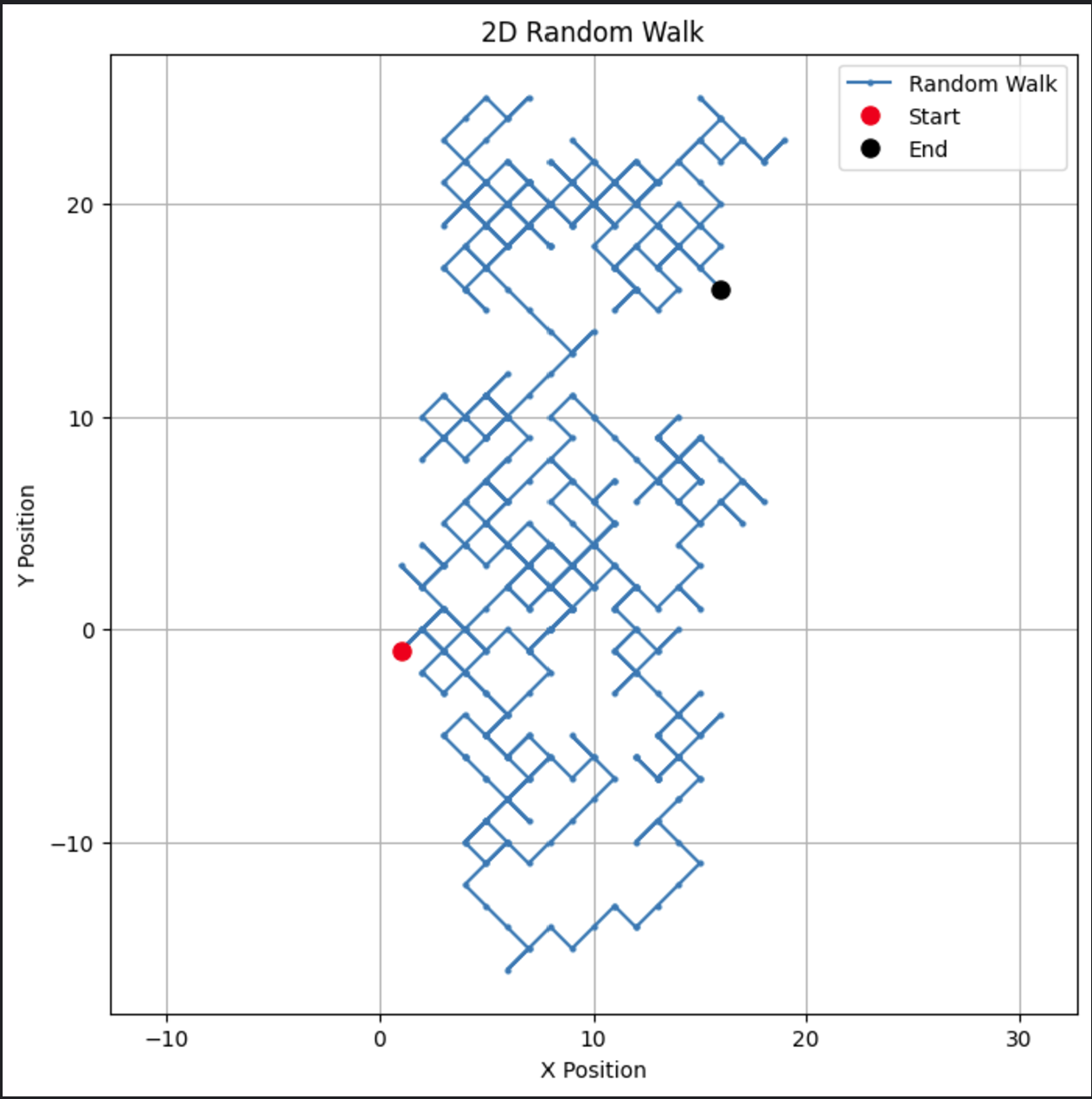
Diese Art von zweidimensionalem Random Walk könnte modifiziert werden, um Anwendungen wie Partikelbewegung oder räumliche Modellierung zu ermöglichen.

Verzerrter Random Walk

Betrachten wir zum Schluss noch ein etwas komplexeres Beispiel: einen verzerrten Random Walk. Um eine Verzerrung einzuführen, können wir die Wahrscheinlichkeiten für jede Schrittrichtung anpassen. Wir können zum Beispiel die Wahrscheinlichkeit von Aufwärtsbewegungen erhöhen.

# Parameters
n_steps = 100
bias = 0.7  # Probability of stepping +1

# Generate biased random steps in x and y directions
x_steps = np.random.choice([-1, 1], size=n_steps, p=[1-bias, bias])
y_steps = np.random.choice([-1, 1], size=n_steps, p=[1-bias, bias])

# Calculate positions
x_positions = np.cumsum(x_steps)
y_positions = np.cumsum(y_steps)

# Plot the biased 2D random walk
plt.figure(figsize=(8, 8))
plt.plot(x_positions, y_positions, marker='o', linestyle='-', markersize=2, label='Random Walk')
plt.plot(x_positions[0], y_positions[0], 'ro', markersize=8, label='Start')  # Red dot for start
plt.plot(x_positions[-1], y_positions[-1], 'ko', markersize=8, label='End')  # Black dot for end
plt.title("Biased 2D Random Walk")
plt.xlabel("X Position")
plt.ylabel("Y Position")
plt.grid(True)
plt.axis('equal')  # Ensures equal scaling for both axes
plt.legend()
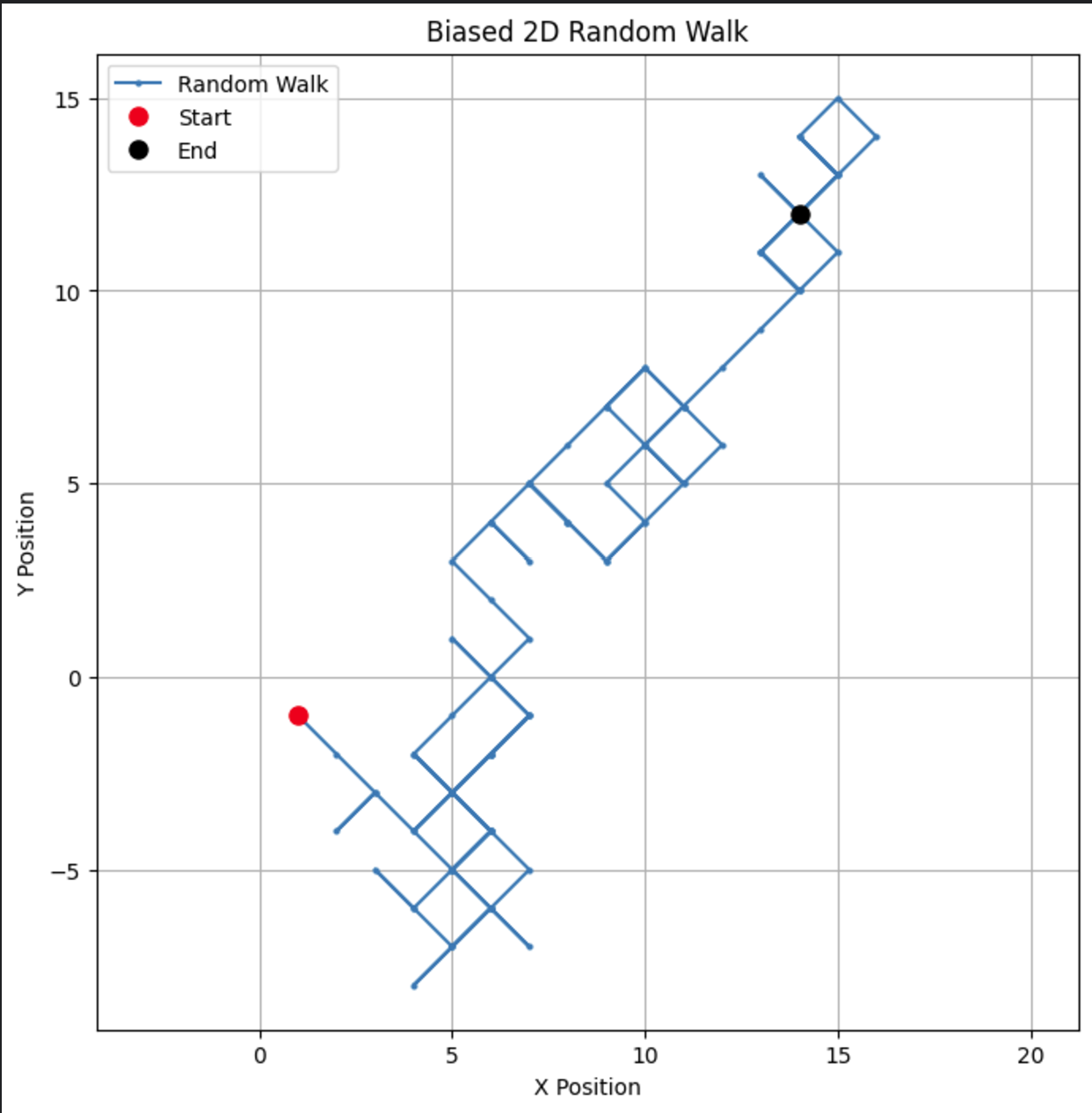
plt.show()

Indem du den Bias änderst, kannst du beobachten, wie der Walk zu einer bestimmten Richtung tendiert, und so reale Szenarien wie die Drift von Aktienkursen oder Tierwanderungen simulieren.

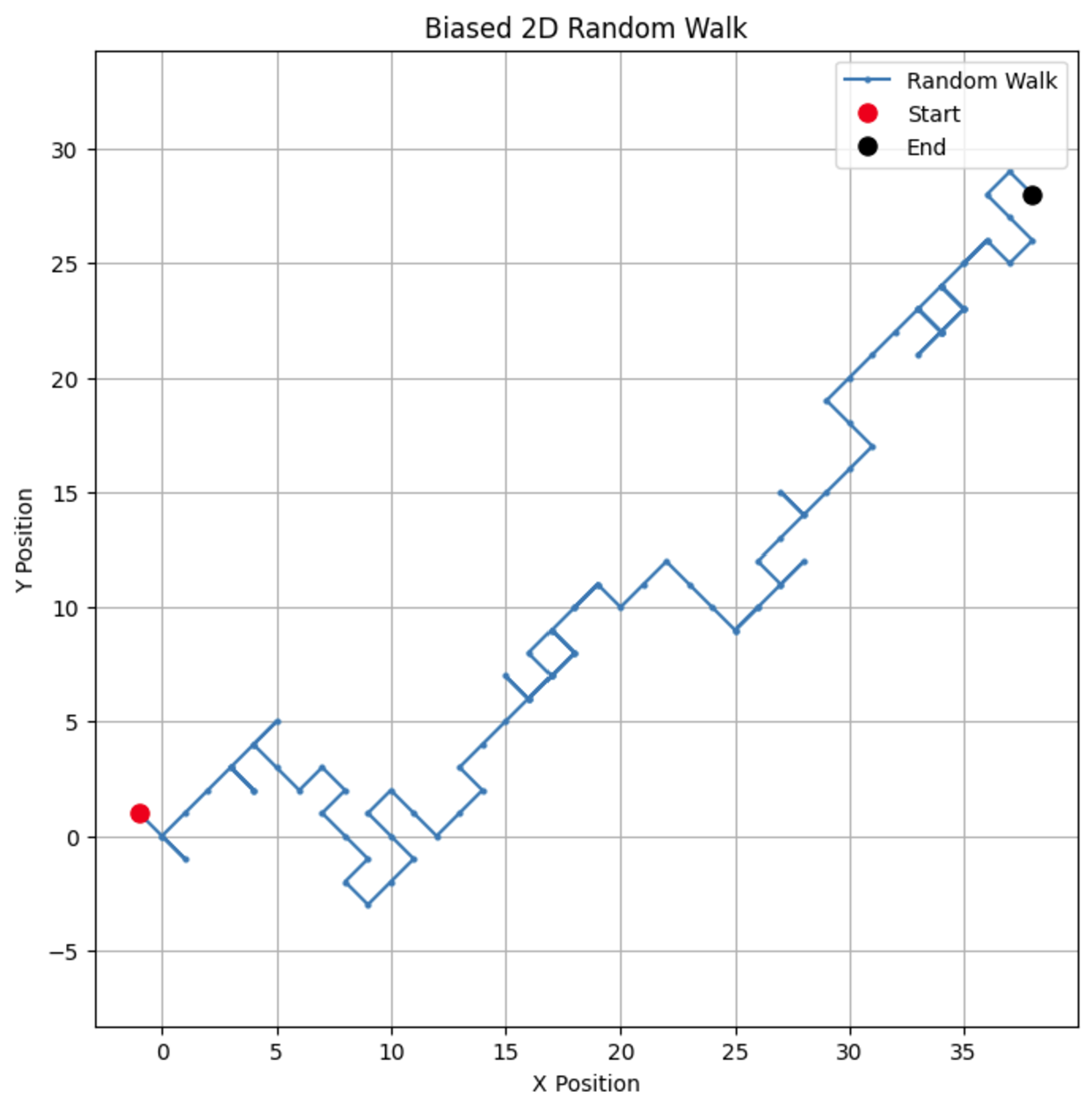
Wenn wir den Bias-Parameter auf 0,55 ändern, können wir einen dramatischen Unterschied im Verhalten des Modells feststellen. Es gibt zwar immer noch eine Tendenz nach oben, aber die Tendenz ist nicht mehr so stark, was zu mehr Schleifen und Umwegen führt.

Fazit

Random Walks sind ein wertvolles Modellierungswerkzeug für Datenwissenschaftler, das in Bereichen von der Physik bis zum Finanzwesen und darüber hinaus Anwendung findet. Ihre Fähigkeit, komplexe, stochastische Prozesse zu modellieren, macht sie in vielen realen Szenarien unverzichtbar.

Hast du Lust auf mehr? Schau dir die DataCamp-Kurse zu Wahrscheinlichkeit und Statistik an. Du findest viele tolle Kurse in Python und R. Wenn du dich für fortgeschrittene Inhalte interessierst, schau dir den DataCamp-Kurs über statistische Simulation in Python und das Tutorial Einführung in maschinelles Lernen an. Wenn du bereit bist, dein Wissen zu testen, kannst du auch einige dieser Wahrscheinlichkeitsrätsel lösen.