Paso a paso al azar: Explorar el modelo de paseo aleatorio

En mi primer curso de estadística basada en la codificación en la universidad, mi profesor propuso una pregunta: ¿cómo podemos modelar el movimiento browniano de una sola partícula de polen en un plato de agua? Tras varios intentos equivocados, mis compañeros y yo acabamos dando con la respuesta correcta: un paseo aleatorio. Más tarde supe que este sencillo modelo se utiliza para modelizar todo tipo de cosas, desde los movimientos de los animales hasta las fluctuaciones de las cotizaciones bursátiles.

En este artículo, exploraremos los fundamentos matemáticos de los paseos aleatorios, examinaremos diferentes tipos y discutiremos sus aplicaciones. Parte de lo que hace interesante al paseo aleatorio es que se utiliza en muchas disciplinas diferentes. Además de mi ejemplo, en física, ayuda a describir el movimiento de las partículas; en finanzas, modela las fluctuaciones de los precios de las acciones; y en biología, explica los patrones de movimiento de los animales. Los paseos aleatorios capturan la aleatoriedad del mundo real, que es clave para simular procesos estocásticos.

Para aquellos que deseen construir una base sólida en la estadística que sustenta la teoría de las caminatas aleatorias, recomendamos empezar con el curso Introducción a la Estadística en R o el curso Introducción a la Estadística en Python.

¿Qué son los Paseos Aleatorios?

En teoría de la probabilidad, un paseo aleatorio es un modelo que describe una secuencia de pasos aleatorios que componen un camino. O bien, podríamos decir que un paseo aleatorio es un modelo matemático que describe una trayectoria formada por una secuencia de pasos, cada uno determinado independientemente y con una probabilidad determinada. Esta estocasticidad hace que los paseos aleatorios sean inherentemente impredecibles.

Imagina que una persona da un paso en una dirección aleatoria en cada momento. Con el tiempo, su camino forma un sendero impredecible y serpenteante. A pesar de su simplicidad, este concepto tiene una profundidad y versatilidad sorprendentes, modelando varios escenarios del mundo real que implican aleatoriedad.

Una explicación conceptual de un paseo aleatorio. Imagen cortesía de napkin.ai.

La idea de los paseos aleatorios se remonta a los primeros estudios de probabilidad. Uno de los primeros ejemplos, a menudo llamado el paseo del borracho, ilustra cómo una persona que pisa al azar deambulará erráticamente en lugar de moverse de forma previsible hacia un destino. Esta aleatoriedad, combinada con el supuesto de que cada paso es independiente de los anteriores, sentó las bases de los modelos modernos de paseo aleatorio.

Comprender las matemáticas de los paseos aleatorios

Para entender los paseos aleatorios, empecemos con un caso sencillo: un paseo aleatorio unidimensional (1D). Imagina una partícula en una recta numérica. Es capaz de desplazarse +1 o -1 a lo largo de la recta numérica con cada paso. Cada movimiento está determinado por una probabilidad igual de dar un paso a la derecha o a la izquierda. Con el tiempo, la posición de la partícula forma una distribución de probabilidad que se extiende, representando la probabilidad de encontrarla en distintos lugares.

Este principio puede ampliarse a dos o tres dimensiones. En un paseo aleatorio bidimensional (2D), la partícula se mueve en un plano y puede pisar en cualquiera de las cuatro direcciones cardinales (arriba, abajo, izquierda, derecha) con igual probabilidad. Del mismo modo, en un paseo aleatorio tridimensional (3D), la partícula se mueve en el espacio y puede pisar en cualquiera de las seis direcciones posibles (arriba, abajo, izquierda, derecha, adelante, atrás) con igual probabilidad. Estos paseos aleatorios de mayor dimensión capturan escenarios aún más complejos y realistas.

Una característica definitoria de los paseos aleatorios es su naturaleza estocástica, lo que significa que cada paso depende sólo de la posición actual y no de los pasos anteriores. Esto los convierte en un tipo de proceso de Markov, un concepto matemático en el que el estado futuro depende únicamente del estado presente, no de la secuencia de acontecimientos que lo precedieron. Este movimiento "sin memoria", combinado con las distribuciones de probabilidad que describen las posiciones potenciales, proporciona una sólida base matemática para comprender los paseos aleatorios.

Podemos analizar un paseo aleatorio utilizando propiedades estadísticas para comprender su comportamiento a lo largo del tiempo. Esto implica examinar aspectos como la distancia esperada desde el punto de partida, la distribución de probabilidad de las posiciones posibles y la probabilidad de volver al origen. Estos análisis nos ayudan a cuantificar la aleatoriedad y la previsibilidad, a comprender los patrones y a hacer predicciones.

Propiedades clave de los paseos aleatorios

Los paseos aleatorios tienen varias propiedades importantes que nos ayudan a comprender su comportamiento y sus aplicaciones. He aquí algunos aspectos clave que debes tener en cuenta:

Expectativa y varianza

En un paseo aleatorio unidimensional, podemos calcular la distancia esperada (o posición media) desde el punto de partida a lo largo del tiempo. Si cada paso tiene la misma probabilidad de moverse hacia la izquierda o hacia la derecha, la posición esperada después de muchos pasos sigue siendo cero, lo que implica que, por término medio, el caminante permanece cerca del punto de partida.

Sin embargo, la varianza de la posición, que mide la dispersión de las posibles posiciones, aumenta con cada paso. Concretamente, en un paseo aleatorio simétrico, la varianza crece linealmente con el número de pasos, lo que la convierte en un indicador útil de la distancia típica desde el origen a lo largo del tiempo.

Autocorrelación

Mientras que los paseos aleatorios simples no tienen correlación entre los pasos (cada paso es independiente del anterior), ciertos tipos de paseos aleatorios introducen autocorrelación, donde los pasos pasados pueden influir en los futuros. Por ejemplo, en un paseo aleatorio sesgado, los pasos pueden tener una ligera tendencia en una dirección, haciendo que las posiciones sean más predecibles.

La autocorrelación en un paseo aleatorio influye en cómo modelamos y predecimos la progresión del paseo. Esto es especialmente relevante en aplicaciones en las que el comportamiento pasado influye en los pasos futuros, como ciertos modelos financieros.

Teorema del límite central

El teorema del límite central (CLT ) nos dice que la suma de un gran número de variables aleatorias independientes tiende a seguir una distribución normal (o gaussiana), independientemente de la distribución original. En el contexto de los paseos aleatorios, esto significa que a medida que aumenta el número de pasos, la distribución de posiciones tiende a parecerse a una distribución normal. Se trata de una propiedad útil porque nos permite aproximar la probabilidad de encontrar al caminante a determinadas distancias del punto de partida.

Ley de los grandes números

La ley de los grandes números (LLN) explica que, a medida que aumenta el número de ensayos o pasos, la media de los resultados converge a la media verdadera. Para los paseos aleatorios, esto significa que, mientras que la posición media sigue siendo cero, la varianza y el rango de posiciones posibles crecen de forma predecible con cada paso adicional. Este principio ayuda a salvar la distancia entre la aleatoriedad pura y los patrones estadísticos predecibles en muestras grandes.

Tipos de recorridos aleatorios

Los paseos aleatorios varían mucho en función de las reglas que rigen cada paso. Estos tipos influyen en el comportamiento de la marcha. Algunos están diseñados para entornos sencillos o estructurados, mientras que otros están equipados para fenómenos más complejos del mundo real. Exploremos algunos de los tipos más comunes de paseos aleatorios.

Paseos aleatorios 1D, 2D y 3D

La dimensionalidad de un paseo aleatorio desempeña un papel fundamental en su comportamiento. En un recorrido aleatorio 1D, cada paso es un avance o un retroceso a lo largo de una línea. Esto hace que la marcha sea relativamente fácil de modelar y predecir.

Sin embargo, a medida que pasamos a recorridos en 2D (plano) y 3D (espacio), las trayectorias posibles aumentan significativamente, introduciendo nuevos comportamientos. Por ejemplo, en un paseo aleatorio 2D, la probabilidad de volver al punto de partida sigue siendo alta, mientras que en un paseo aleatorio 3D, esta probabilidad disminuye.

Este cambio es importante en campos como la física y la química, donde las partículas pueden difundirse de forma diferente en función de las restricciones dimensionales.

Recorrido aleatorio reticular

En un paseo aleatorio reticular, el movimiento se limita a puntos discretos de una rejilla o celosía. Este tipo de recorrido se utiliza habitualmente en física y teoría de redes, donde los nodos están dispuestos en una cuadrícula, y el movimiento sólo puede producirse hacia los nodos vecinos.

Un ejemplo habitual es un entramado 2D, en el que cada paso permite el movimiento a puntos adyacentes de una rejilla cartesiana. Esta restricción simplifica el modelado al limitar las rutas de movimiento, lo que resulta útil cuando se simulan redes o estructuras moleculares complejas.

Recorrido aleatorio gaussiano

En un recorrido aleatorio gaussiano, el tamaño de cada paso viene determinado por una distribución gaussiana (o normal). En lugar de desplazarse una distancia fija, el tamaño del paso varía según una distribución en forma de curva de campana, con la mayoría de los pasos pequeños y saltos ocasionales más grandes. Este tipo de recorrido se utiliza con frecuencia en la modelización financiera para tener en cuenta la variabilidad de las variaciones de los precios de los activos.

Caminatas aleatorias heterogéneas y sesgadas

Los paseos aleatorios heterogéneos y sesgados permiten variar la dirección y el tamaño de los pasos en función de determinadas probabilidades. Esta flexibilidad las hace más adaptables a los escenarios del mundo real.

En un paseo aleatorio heterogéneo, la probabilidad de moverse en cualquier dirección puede cambiar en función de la ubicación o de las condiciones externas. Por ejemplo, los animales que buscan comida pueden favorecer zonas con recursos conocidos, creando un paseo aleatorio sesgado. Estos paseos son útiles para estudiar comportamientos que dependen de factores contextuales.

Paseo aleatorio con deriva

En un paseo aleatorio con deriva, hay una tendencia constante a moverse en una dirección. Por ejemplo, los precios de las acciones pueden mostrar una tendencia general al alza a lo largo del tiempo, a pesar de las fluctuaciones diarias. La deriva en estos paseos representa una fuerza o tendencia externa que influye en la trayectoria. Este tipo se ve a menudo en finanzas, donde los modelos incorporan un término de deriva para representar el crecimiento o el declive, proporcionando un enfoque más realista para predecir los precios de los activos y las tendencias del mercado.

Cada uno de estos tipos de camino aleatorio sirve a un propósito único, ofreciendo diferentes formas de modelar el comportamiento aleatorio, aunque estructurado. Las restricciones dimensionales, la distribución de los pasos y la presencia de deriva o sesgo hacen que los paseos aleatorios sean muy versátiles para el modelado y la simulación de datos en distintos campos.

Aplicaciones reales de los paseos aleatorios

Los paseos aleatorios son algo más que construcciones teóricas; desempeñan un papel esencial en muchas aplicaciones prácticas de distintas disciplinas. Exploremos cómo los paseos aleatorios informan la resolución de problemas del mundo real en todos los sectores.

Aplicaciones en ciencia de datos y aprendizaje automático

Informática

Los paseos aleatorios sustentan varios algoritmos informáticos, como el muestreo aleatorio, el recorrido de grafos web y la segmentación de imágenes. Por ejemplo, el algoritmo PageRank de Google utilizaba paseos aleatorios para clasificar las páginas web en función de su relevancia, simulando cómo un usuario podría navegar aleatoriamente entre enlaces en Internet.

Extracción de rasgos

En el aprendizaje automático, los paseos aleatorios pueden ayudar a extraer características resaltando las relaciones dentro de los puntos de datos. Por ejemplo, en el análisis de redes, los paseos aleatorios pueden revelar conglomerados o comunidades, ayudando en tareas como los sistemas de recomendación y el análisis de redes sociales.

Detección de anomalías

Los paseos aleatorios también pueden utilizarse para detectar anomalías en conjuntos de datos. Por ejemplo, si los puntos de datos se desvían significativamente de una trayectoria típica en un modelo de camino aleatorio, estos puntos podrían indicar sucesos inusuales o errores en los datos. La detección de anomalías es especialmente valiosa en campos como la ciberseguridad y la detección del fraude.

Simulación de procesos estocásticos

Los paseos aleatorios simulan procesos estocásticos, o determinados aleatoriamente, lo que permite a los científicos de datos modelizar fenómenos impredecibles del mundo real. Mediante la simulación de paseos aleatorios, podemos obtener información sobre sistemas en los que la predicción precisa es un reto, como los patrones meteorológicos o el comportamiento de los clientes.

Previsión de series temporales

En el análisis de series temporales, los paseos aleatorios constituyen la base de ciertos modelos de previsión, incluida la hipótesis del paseo aleatorio en finanzas. Estos modelos suponen que los valores futuros de una serie temporal dependen únicamente del valor más reciente, sin correlación con las tendencias pasadas. Para saber más sobre la previsión de series temporales, consulta ARIMA para la previsión de series temporales: Guía completa. Además, sigue nuestro curso de Previsión en R con el profesor Hyndman, que conecta los modelos de paseo aleatorio con los métodos de previsión ingenuos e ingenuos estacionales.

Aplicaciones en otros campos

Finanzas

Uno de los usos más notables de las caminatas aleatorias es la modelización financiera, especialmente para predecir los precios de las acciones. La hipótesis del mercado eficiente sugiere que los movimientos de los precios de las acciones son esencialmente aleatorios, ya que la nueva información se absorbe instantáneamente, lo que hace que los precios futuros sean impredecibles. Los paseos aleatorios pueden utilizarse para modelizar las variaciones del precio de las acciones a lo largo del tiempo, ilustrando cómo fluctúan los precios sin una trayectoria predecible.

Matemáticas

En matemáticas puras, los paseos aleatorios proporcionan soluciones a problemas complejos. Por ejemplo, son útiles para resolver la ecuación de Laplace, analizar redes y explorar la combinatoria.

Física y química

En las ciencias físicas, los paseos aleatorios son cruciales para modelar los procesos de difusión, como la forma en que las moléculas se propagan por un medio. El movimiento browniano, en el que las partículas suspendidas en un fluido se mueven de forma impredecible debido a las colisiones con las moléculas circundantes, es un ejemplo clásico que puede simularse con precisión utilizando paseos aleatorios. En realidad, así es como aprendí por primera vez sobre los paseos aleatorios.

Biología

Los paseos aleatorios son valiosos en ecología para estudiar las pautas de movimiento de los animales. Puede parecer que los animales que buscan recursos se mueven en un paseo aleatorio, a veces sesgado hacia regiones con recursos conocidos. Otros conceptos biológicos, como la propagación de poblaciones o genes, pueden modelarse a menudo con principios de paseo aleatorio, lo que facilita la comprensión y la predicción de los cambios dentro de los ecosistemas.

Casos especiales y variantes de los paseos aleatorios

Además del paseo aleatorio clásico, diversas variantes avanzadas amplían el concepto para adaptarlo a aplicaciones especializadas.

Paseos auto-evitativos

Un recorrido autoevitador es un recorrido aleatorio en el que la trayectoria no vuelve a visitar ninguna posición por la que ya haya pasado. Esta variante es especialmente útil en campos como la química de polímeros, donde puede modelizar cómo se forman las cadenas de polímeros sin cruzarse entre sí. Como cada paso evita los puntos visitados anteriormente, los paseos auto-evitadores están más limitados que los paseos aleatorios tradicionales. Esto significa que son computacionalmente desafiantes, pero útiles para comprender las trayectorias no solapadas en espacios reducidos.

Ramificación

En los paseos aleatorios ramificados, el camino puede dividirse en múltiples ramas, y cada rama sigue un paseo aleatorio. Este tipo de recorrido es fundamental para modelar procesos de ramificación, como la división celular o la propagación de información a través de redes. Cada "rama" representa una trayectoria aleatoria independiente que se origina a partir de una fuente común.

Paseos correlacionados

Los paseos correlacionados llevan este concepto un paso más allá, donde la dirección de cada paso está parcialmente influida por el paso anterior. Esta variante es útil para modelar la inercia en sistemas en los que los cambios se producen de forma gradual y no aleatoria. Los paseos correlacionados se aplican a menudo en finanzas para simular las tendencias de los precios o en ecología del movimiento para comprender cómo los animales navegan por su entorno con cierta memoria de su dirección pasada.

Paseos con bucle borrado

Una marcha con borrado de bucles es una variante en la que los bucles, o caminos que se cruzan, se eliminan a medida que se forman. Cada vez que un paso vuelve a visitar una posición, el bucle intermedio se borra, dejando una trayectoria aerodinámica y no repetitiva. Los paseos con borrado de bucles se aplican habitualmente en los algoritmos de análisis de redes y generación de laberintos, porque crean caminos que evitan la redundancia.

Implementar paseos aleatorios en Python

Intentemos implementar un paseo aleatorio en Python. Para empezar, asegúrate de que tienes Python instalado (utilizaremos Python 3.10) y las bibliotecas necesarias disponibles. Puedes instalar las bibliotecas que te falten utilizando pip. Esto es lo que utilizaremos:

import numpy as np # for numerical operations and generating random steps
import matplotlib.pyplot as plt # for plotting and visualizing the random walks

Recorrido aleatorio 1D

Empezaremos con un simple paseo aleatorio unidimensional, en el que cada paso es +1 o -1, elegidos al azar.

# Parameters
n_steps = 100  # Number of steps

# Generate random steps: +1 or -1
steps = np.random.choice([-1, 1], size=n_steps)

# Calculate positions
positions = np.cumsum(steps)

# Plot the random walk
plt.figure(figsize=(10, 6))
plt.plot(positions, marker='o', linestyle='-', markersize=4)
plt.title("1D Random Walk")
plt.xlabel("Step")
plt.ylabel("Position")
plt.grid(True)
plt.show()

Esto genera un simple paseo aleatorio y visualiza la progresión en el tiempo. Este es el resultado cuando ejecuto este código:

Ahora recuerda que estamos ejecutando un modelo estocástico. Esto significa que cada vez que lo ejecutemos, el resultado será un poco diferente.

Recorrido aleatorio 2D

Ahora ampliemos el paseo aleatorio a dos dimensiones. En cada paso, la dirección se elegirá aleatoriamente.

# Parameters
n_steps = 500

# Generate random steps in x and y directions
x_steps = np.random.choice([-1, 1], size=n_steps)
y_steps = np.random.choice([-1, 1], size=n_steps)

# Calculate positions
x_positions = np.cumsum(x_steps)
y_positions = np.cumsum(y_steps)

# Plot the 2D random walk
plt.figure(figsize=(8, 8))
plt.plot(x_positions, y_positions, marker='o', linestyle='-', markersize=2, label='Random Walk')
plt.plot(x_positions[0], y_positions[0], 'ro', markersize=8, label='Start')  # Red dot for start
plt.plot(x_positions[-1], y_positions[-1], 'ko', markersize=8, label='End')  # Black dot for end
plt.title("2D Random Walk")
plt.xlabel("X Position")
plt.ylabel("Y Position")
plt.grid(True)
plt.axis('equal')  # Ensures equal scaling for both axes
plt.legend()
plt.show()

Este código crea un recorrido visualmente atractivo en dos dimensiones.

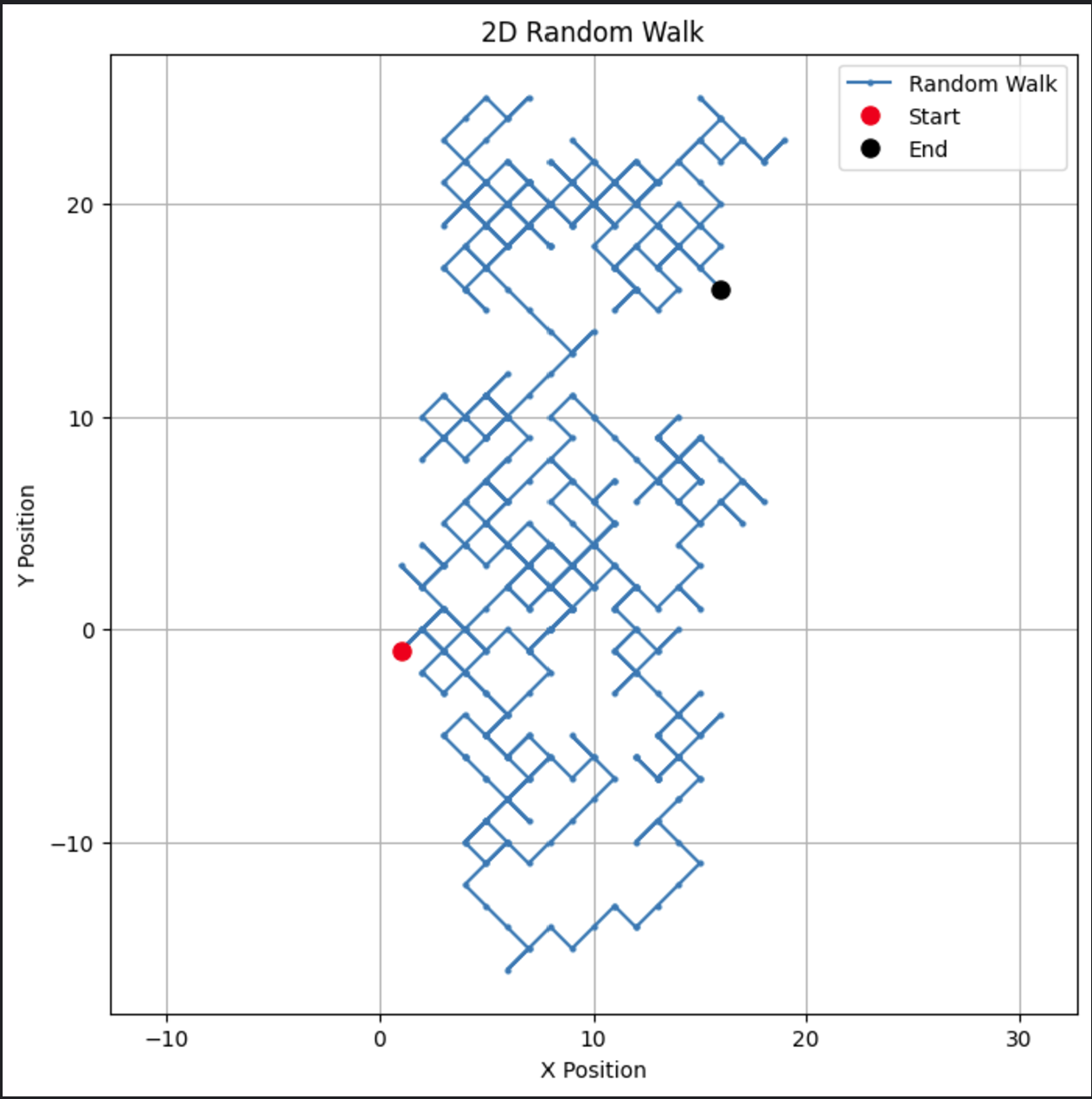
Este tipo de paseo aleatorio bidimensional podría modificarse para adaptarse a aplicaciones como el movimiento de partículas o el modelado espacial.

Paseo aleatorio sesgado

Por último, veamos un ejemplo algo más complejo: un paseo aleatorio sesgado. Para introducir el sesgo, podemos ajustar las probabilidades de cada dirección de paso. Por ejemplo, podríamos hacer más probables los pasos hacia arriba.

# Parameters
n_steps = 100
bias = 0.7  # Probability of stepping +1

# Generate biased random steps in x and y directions
x_steps = np.random.choice([-1, 1], size=n_steps, p=[1-bias, bias])
y_steps = np.random.choice([-1, 1], size=n_steps, p=[1-bias, bias])

# Calculate positions
x_positions = np.cumsum(x_steps)
y_positions = np.cumsum(y_steps)

# Plot the biased 2D random walk
plt.figure(figsize=(8, 8))
plt.plot(x_positions, y_positions, marker='o', linestyle='-', markersize=2, label='Random Walk')
plt.plot(x_positions[0], y_positions[0], 'ro', markersize=8, label='Start')  # Red dot for start
plt.plot(x_positions[-1], y_positions[-1], 'ko', markersize=8, label='End')  # Black dot for end
plt.title("Biased 2D Random Walk")
plt.xlabel("X Position")
plt.ylabel("Y Position")
plt.grid(True)
plt.axis('equal')  # Ensures equal scaling for both axes
plt.legend()
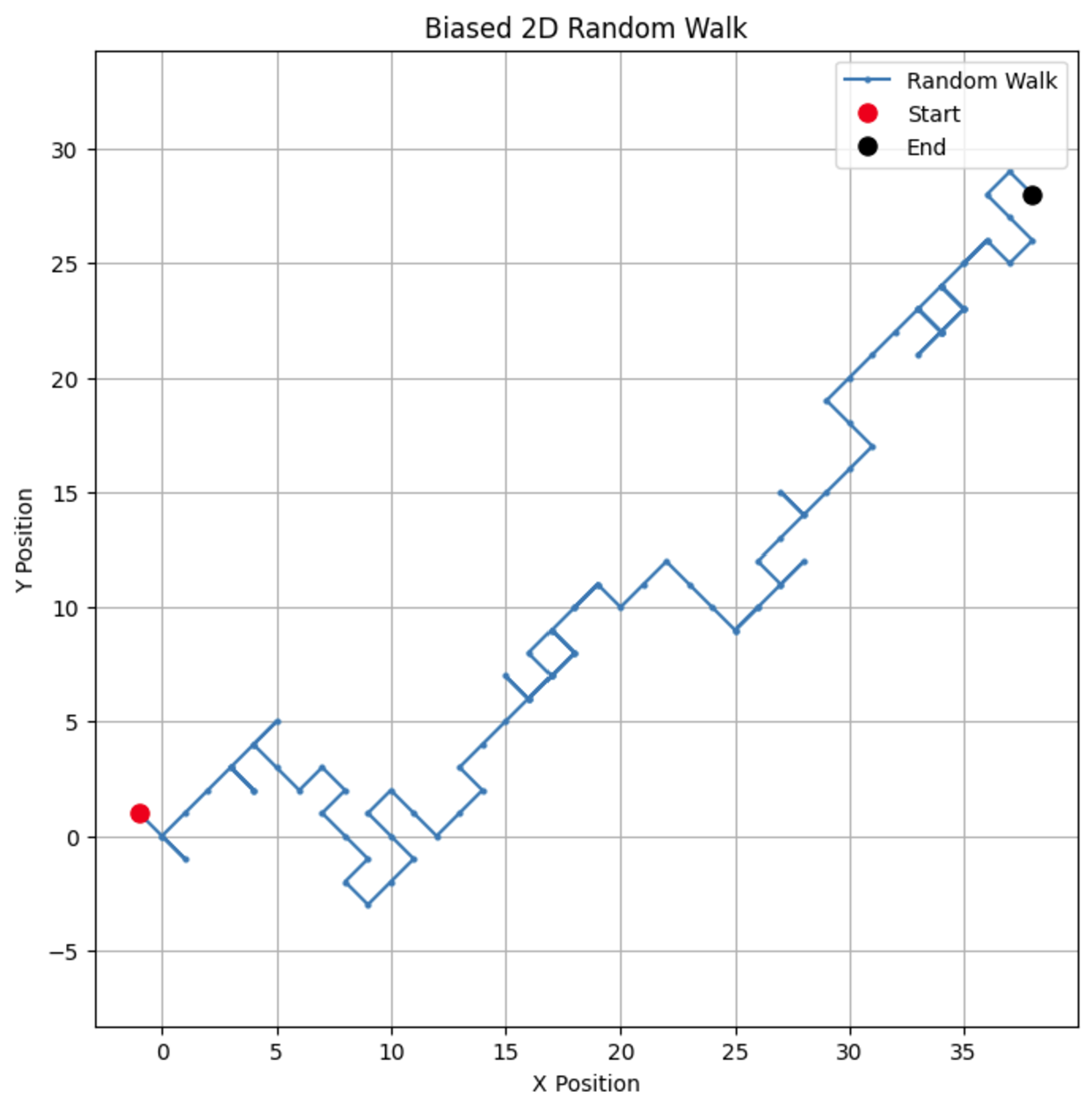
plt.show()

Cambiando el sesgo, puedes observar cómo el paseo tiende a favorecer una dirección concreta, simulando escenarios del mundo real como la deriva de los precios de las acciones o los patrones de migración de los animales.

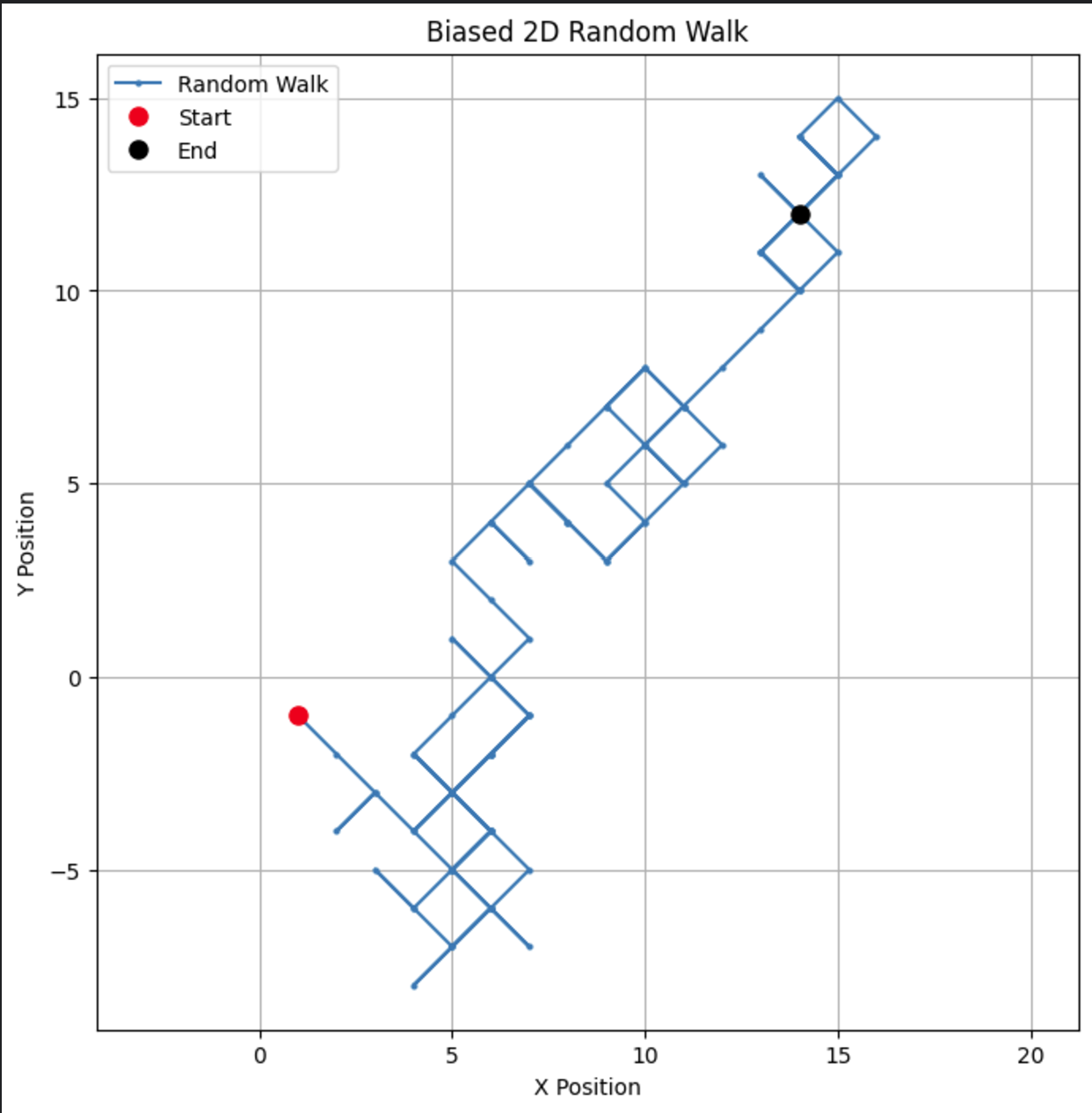
Si cambiamos el parámetro de sesgo a 0,55, podemos ver una diferencia drástica en la forma en que se comporta el modelo. Aunque sigue teniendo tendencia a subir, ésta no es tan fuerte, lo que da lugar a más bucles y desvíos.

Conclusión

Los paseos aleatorios son una valiosa herramienta de modelización para los científicos de datos, aplicable en campos que van desde la física a las finanzas y más allá. Su capacidad para modelar procesos estocásticos complejos los hace indispensables en muchos escenarios del mundo real.

¿Tienes ganas de más? Echa un vistazo al conjunto de cursos de probabilidad y estadística de DataCamp. Encontrarás todo tipo de cursos estupendos tanto en Python como en R. Si te interesan contenidos más avanzados, echa un vistazo al curso de DataCamp sobre Simulación Estadística en Python y al tutorial Introducción al Aprendizaje Automático. O si estás preparado para poner a prueba tus conocimientos, enfréntate a algunos de estos acertijos de probabilidad.