Introduction aux modèles linéaires
Pratiquez le Lasso et la régression de crête en Python avec cet exercice pratique.
La régression linéaire est un type de modèle linéaire considéré comme l'algorithme prédictif le plus élémentaire et le plus couramment utilisé. Ceci est indissociable de son architecture simple mais efficace. Un modèle linéaire suppose une relation linéaire entre la ou les variables d'entrée 𝑥 et une variable de sortie y. L'équation d'un modèle linéaire se présente comme suit :
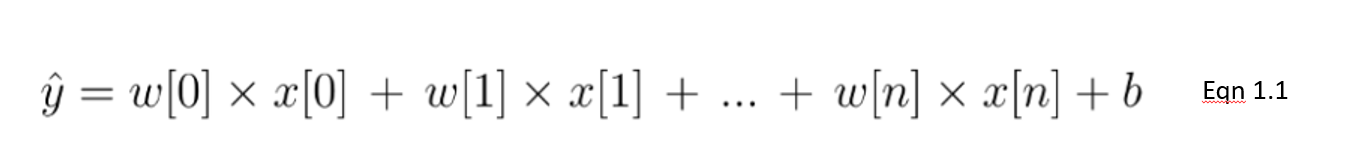
Dans cette équation 1.1, nous présentons un modèle linéaire avec un nombre n de caractéristiques. w est considéré comme le coefficient (ou les poids) attribué à chaque caractéristique - un indicateur de leur importance pour le résultat y. Par exemple, nous supposons que la température est un facteur plus important pour les ventes de glaces que le fait qu'il s'agisse d'un jour férié. Le poids attribué à la température dans notre modèle linéaire sera plus important que celui de la variable des jours fériés.
L'objectif d'un modèle linéaire est alors d'optimiser le poids (b) via la fonction de coût de l'équation 1.2. La fonction de coût calcule l'erreur entre les prédictions et les valeurs réelles, représentée par un seul nombre à valeur réelle. La fonction de coût est l'erreur moyenne sur les n échantillons de l'ensemble de données, représentée ci-dessous comme suit :
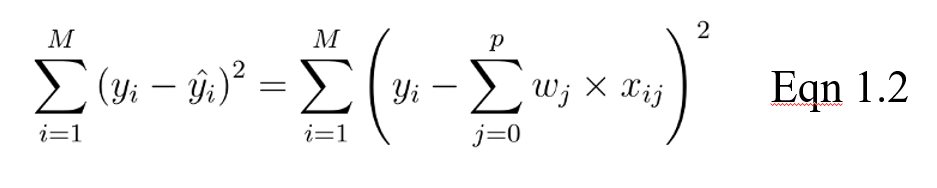
Dans l'équation ci-dessus, yi est la valeur réelle et c'est la valeur prédite par notre équation linéaire, où M est le nombre de lignes et P le nombre de caractéristiques.
Régularisation
Lorsqu'il s'agit de former des modèles, deux problèmes majeurs peuvent se poser : l'overfitting et l'underfitting.
- Il y a surajustement lorsque le modèle est performant sur l'ensemble d'apprentissage mais moins bien sur les données non vues (test).
- Il y a sous-adaptation lorsqu'il n'y a pas de bonnes performances sur l'ensemble de formation ni sur l'ensemble de test.
En particulier, la régularisation est mise en œuvre pour éviter l'ajustement excessif des données, surtout lorsqu'il existe une grande variance entre les performances de l'ensemble de formation et de l'ensemble de test. Avec la régularisation, le nombre de caractéristiques utilisées dans la formation reste constant, mais l'ampleur des coefficients (w), comme le montre l'équation 1.1, est réduite.
Considérez l'image des coefficients ci-dessous pour prédire les prix de l'immobilier. Bien qu'il y ait un grand nombre de variables prédictives, RM et RAD ont les coefficients les plus importants. Cela signifie que les prix du logement seront davantage influencés par ces deux caractéristiques, ce qui entraînera un surajustement, c'est-à-dire que l'on n'aura pas appris de modèles généralisables.
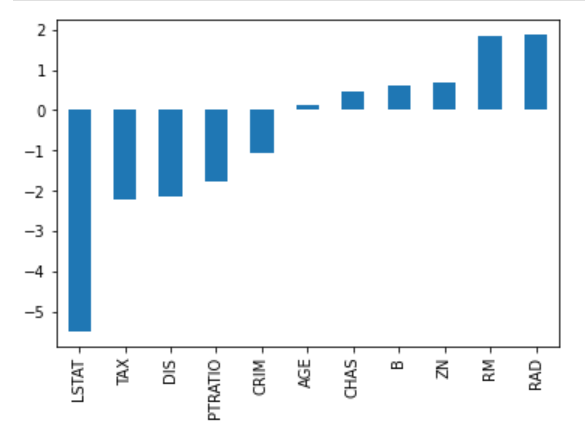
Il existe différentes façons de réduire la complexité des modèles et d'éviter l'ajustement excessif dans les modèles linéaires. Cela inclut les modèles de régression ridge et lasso.
Introduction à la régression Lasso
Il s'agit d'une technique de régularisation utilisée dans la sélection des caractéristiques à l'aide d'une méthode de rétrécissement également appelée méthode de régression pénalisée. Lasso est l'abréviation de Least Absolute Shrinkageand Selection Operator, qui est utilisé à la fois pour la régularisation et la sélection de modèles. Si un modèle utilise la technique de régularisation L1, il s'agit alors d'une régression lasso.
Régression Lasso pour la régularisation
Dans cette technique de rétrécissement, les coefficients déterminés dans le modèle linéaire de l'équation 1.1. ci-dessus sont rétrécis vers le point central comme la moyenne en introduisant un facteur de pénalisation appelé les valeurs alpha α (ou parfois lamda).
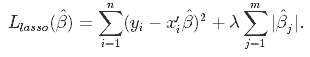
Alpha (α) est le terme de pénalité qui indique le degré de rétrécissement (ou de contrainte) qui sera mis en œuvre dans l'équation. Si alpha est fixé à zéro, vous constaterez qu'il s'agit de l'équivalent du modèle de régression linéaire de l'équation 1.2, et qu'une valeur plus élevée pénalise la fonction d'optimisation. Par conséquent, la régression lasso réduit les coefficients et contribue à réduire la complexité du modèle et la multicollinéarité.
Alpha (α) peut être un nombre réel compris entre zéro et l'infini ; plus la valeur est grande, plus la pénalisation est agressive.
Régression Lasso pour la sélection de modèles
Les coefficients étant ramenés à une moyenne de zéro, les caractéristiques les moins importantes d'un ensemble de données sont éliminées lorsqu'elles sont pénalisées. Le rétrécissement de ces coefficients sur la base de la valeur alpha fournie conduit à une certaine forme de sélection automatique des caractéristiques, les variables d'entrée étant supprimées dans le cadre d'une approche efficace.
Régression des crêtes
Comme la régression lasso, la régression ridge impose une contrainte similaire sur les coefficients en introduisant un facteur de pénalité. Cependant, alors que la régression lasso prend en compte l'ampleur des coefficients, la régression ridge prend en compte le carré.
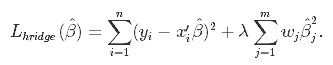
La régression ridge est également appelée régularisation L2.
Pourquoi le Lasso peut être utilisé pour la sélection de modèles, mais pas pour la régression Ridge ?
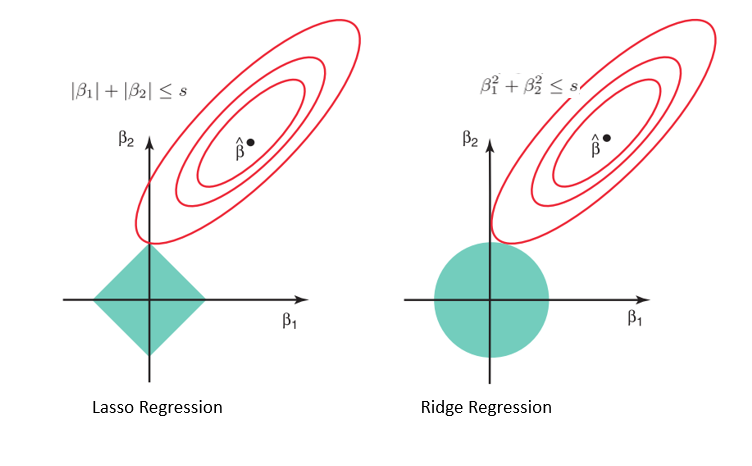
Compte tenu de la géométrie des modèles lasso (à gauche) et ridge (à droite), les contours elliptiques (cercles rouges) représentent les fonctions de coût pour chacun d'entre eux. L'assouplissement des contraintes introduites par le facteur de pénalité entraîne une augmentation de la région contrainte (losange, cercle). En procédant ainsi continuellement, nous atteindrons le centre de l'ellipse, où les résultats des modèles lasso et ridge sont similaires à ceux d'un modèle de régression linéaire.
Cependant, les deux méthodes déterminent les coefficients en trouvant le premier point où les contours elliptiques touchent la région des contraintes. Étant donné que la régression lasso prend la forme d'un diamant dans le graphique pour la région contrainte, chaque fois que les régions elliptiques se croisent avec ces coins, au moins un des coefficients devient nul. Cela est impossible dans le modèle de régression par crête, car il a une forme circulaire et, par conséquent, les valeurs peuvent être rapprochées de zéro, mais jamais égales à zéro.
Mise en œuvre de Python
Pour cette mise en œuvre, nous utiliserons l'ensemble de données sur le logement de Boston que l'on trouve dans Sklearn. Ce que nous voulons voir, c'est :
- Comment effectuer une régression ridge et lasso en Python
- Comparez les résultats avec un modèle de régression linéaire
Importation de données et EDA
#libraries
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import Ridge, RidgeCV, Lasso
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import load_boston
#data
boston = load_boston()
boston_df=pd.DataFrame(boston.data,columns=boston.feature_names)
#target variable
boston_df['Price']=boston.target
#preview
boston_df.head()
#Exploration
plt.figure(figsize = (10, 10))
sns.heatmap(boston_df.corr(), annot = True)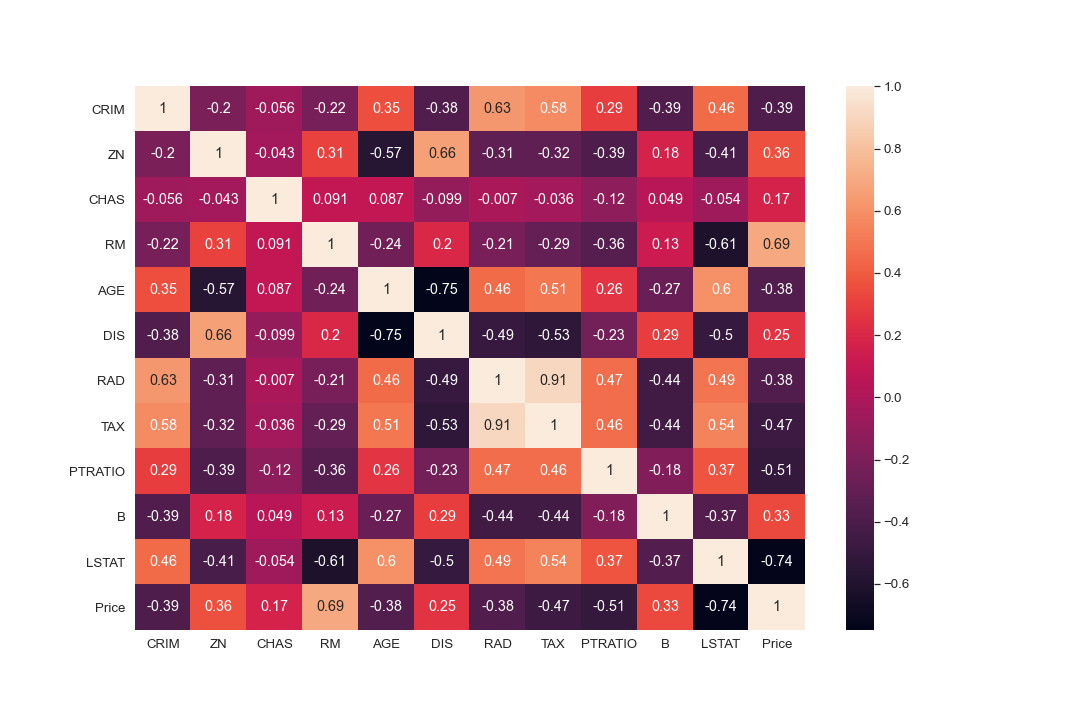
#There are cases of multicolinearity, we will drop a few columns
boston_df.drop(columns = ["INDUS", "NOX"], inplace = True)
#pairplot
sns.pairplot(boston_df)
#we will log the LSTAT Column
boston_df.LSTAT = np.log(boston_df.LSTAT)
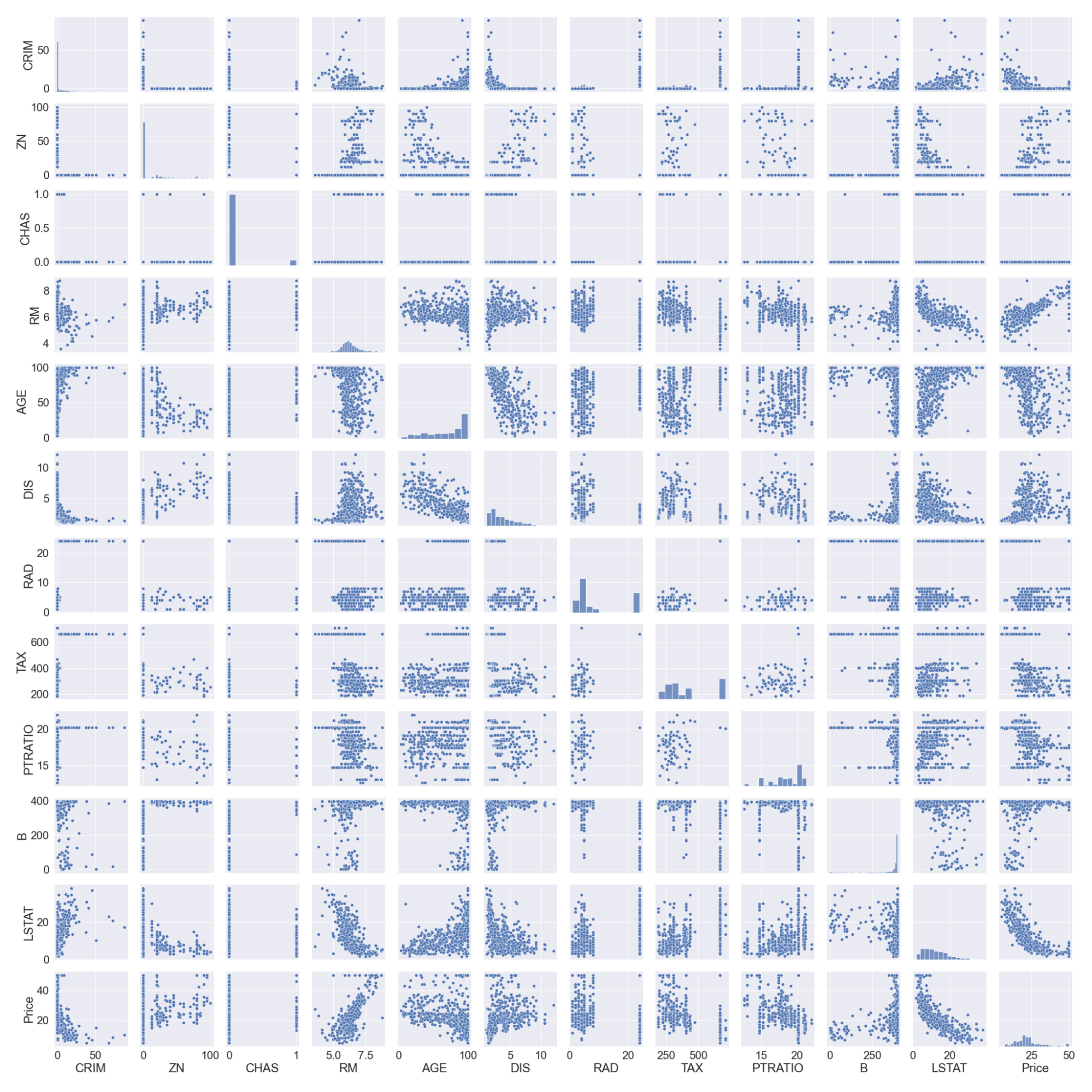
Notez que nous avons enregistré la colonne LSTAT car elle n'a pas de relation linéaire avec la colonne prix. Les modèles linéaires supposent une relation linéaire entre les variables x et y.
Fractionnement et mise à l'échelle des données
#preview
features = boston_df.columns[0:11]
target = boston_df.columns[-1]
#X and y values
X = boston_df[features].values
y = boston_df[target].values
#splot
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=17)
print("The dimension of X_train is {}".format(X_train.shape))
print("The dimension of X_test is {}".format(X_test.shape))
#Scale features
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)
Sortie :

Modèles de régression linéaire et de crête
Nous construirons un modèle de régression linéaire et un modèle de régression par crête, puis nous comparerons les coefficients dans un graphique. Le score des ensembles de formation et de test nous aidera également à évaluer les performances du modèle.
#Model
lr = LinearRegression()
#Fit model
lr.fit(X_train, y_train)
#predict
#prediction = lr.predict(X_test)
#actual
actual = y_test
train_score_lr = lr.score(X_train, y_train)
test_score_lr = lr.score(X_test, y_test)
print("The train score for lr model is {}".format(train_score_lr))
print("The test score for lr model is {}".format(test_score_lr))
#Ridge Regression Model
ridgeReg = Ridge(alpha=10)
ridgeReg.fit(X_train,y_train)
#train and test scorefor ridge regression
train_score_ridge = ridgeReg.score(X_train, y_train)
test_score_ridge = ridgeReg.score(X_test, y_test)
print("\nRidge Model............................................\n")
print("The train score for ridge model is {}".format(train_score_ridge))
print("The test score for ridge model is {}".format(test_score_ridge))

En utilisant une valeur alpha de 10, l'évaluation du modèle, les données de formation et de test indiquent une meilleure performance du modèle de crête que du modèle de régression linéaire.
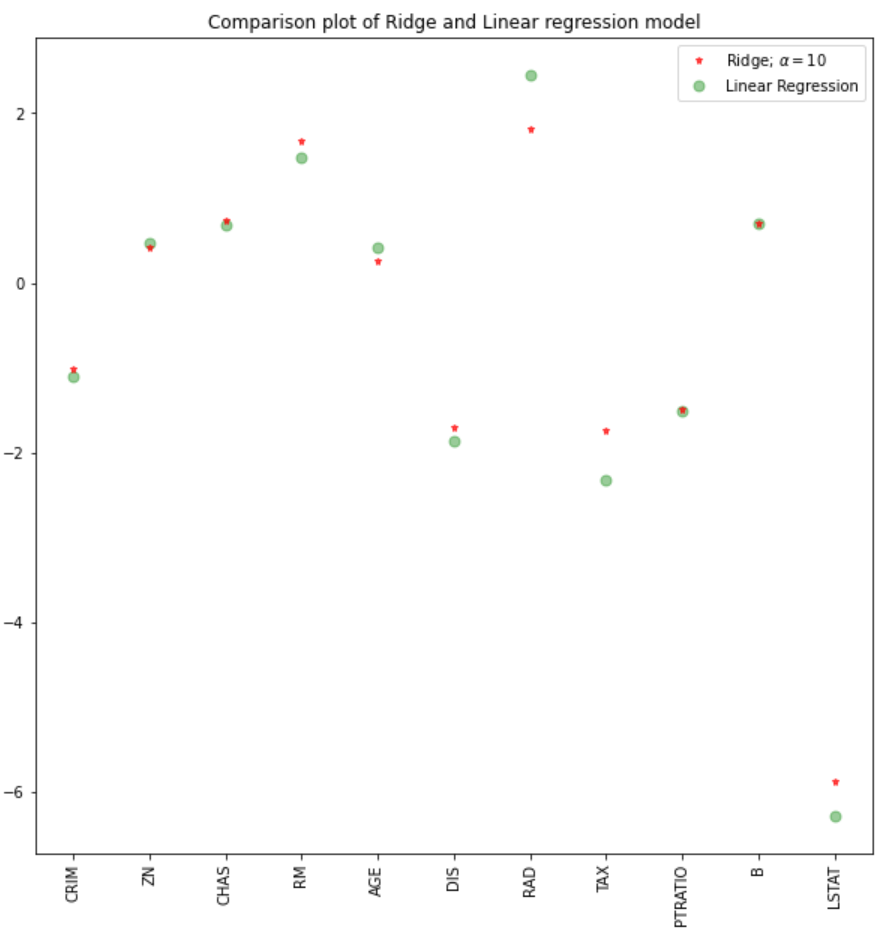
Nous pouvons également tracer les coefficients pour les modèles linéaire et de crête.
plt.figure(figsize = (10, 10))
plt.plot(features,ridgeReg.coef_,alpha=0.7,linestyle='none',marker='*',markersize=5,color='red',label=r'Ridge; $\alpha = 10$',zorder=7)
#plt.plot(rr100.coef_,alpha=0.5,linestyle='none',marker='d',markersize=6,color='blue',label=r'Ridge; $\alpha = 100$')
plt.plot(features,lr.coef_,alpha=0.4,linestyle='none',marker='o',markersize=7,color='green',label='Linear Regression')
plt.xticks(rotation = 90)
plt.legend()
plt.show()
Régression Lasso
#Lasso regression model
print("\nLasso Model............................................\n")
lasso = Lasso(alpha = 10)
lasso.fit(X_train,y_train)
train_score_ls =lasso.score(X_train,y_train)
test_score_ls =lasso.score(X_test,y_test)
print("The train score for ls model is {}".format(train_score_ls))
print("The test score for ls model is {}".format(test_score_ls))

Nous pouvons également visualiser les coefficients.
pd.Series(lasso.coef_, features).sort_values(ascending = True).plot(kind = "bar")
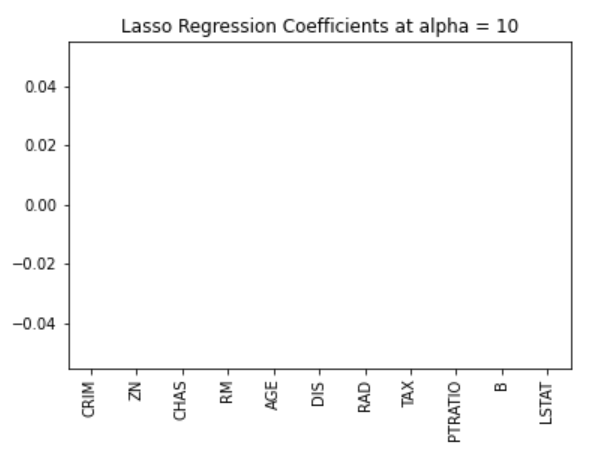
Plus tôt, nous avons établi que le modèle lasso peut être inerte à zéro en raison de la forme de diamant de la région de contrainte. Dans ce cas, l'utilisation d'une valeur alpha de 10 pénalise excessivement le modèle et ramène toutes les valeurs à zéro. Nous pouvons nous en rendre compte en visualisant les coefficients du modèle, comme le montre la figure ci-dessus.
Sélection des valeurs alpha optimales par validation croisée dans Sklearn
Il se peut que nous devions essayer différentes valeurs alpha pour trouver la valeur optimale de la contrainte. Dans ce cas, nous pouvons utiliser le modèle de validation croisée du logiciel sklearn. Il s'agit d'essayer différentes combinaisons de valeurs alpha et de choisir le meilleur modèle.
#Using the linear CV model
from sklearn.linear_model import LassoCV
#Lasso Cross validation
lasso_cv = LassoCV(alphas = [0.0001, 0.001,0.01, 0.1, 1, 10], random_state=0).fit(X_train, y_train)
#score
print(lasso_cv.score(X_train, y_train))
print(lasso_cv.score(X_test, y_test))
Sortie :

Le modèle sera entraîné sur différentes valeurs alpha que j'ai spécifiées dans la fonction LassoCV. Nous pouvons observer une meilleure performance du modèle, en supprimant l'effort fastidieux de modifier manuellement les valeurs alpha.
Nous pouvons comparer les coefficients du modèle lasso avec les autres modèles (linéaire et ridge).
#plot size
plt.figure(figsize = (10, 10))
#add plot for ridge regression
plt.plot(features,ridgeReg.coef_,alpha=0.7,linestyle='none',marker='*',markersize=5,color='red',label=r'Ridge; $\alpha = 10$',zorder=7)
#add plot for lasso regression
plt.plot(lasso_cv.coef_,alpha=0.5,linestyle='none',marker='d',markersize=6,color='blue',label=r'lasso; $\alpha = grid$')
#add plot for linear model
plt.plot(features,lr.coef_,alpha=0.4,linestyle='none',marker='o',markersize=7,color='green',label='Linear Regression')
#rotate axis
plt.xticks(rotation = 90)
plt.legend()
plt.title("Comparison plot of Ridge, Lasso and Linear regression model")
plt.show()
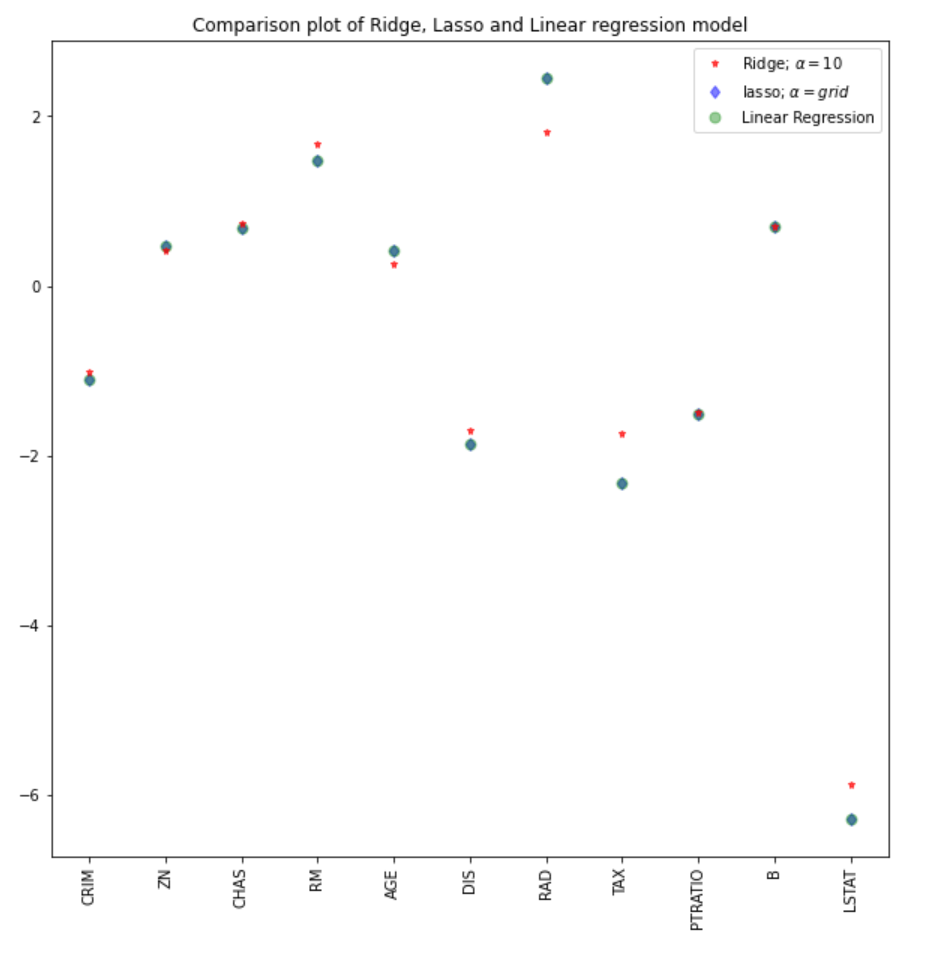
Note: Une approche similaire pourrait être employée pour le modèle de régression ridge, ce qui pourrait conduire à de meilleurs résultats. Dans le package sklearn, la fonction RidgeCV fonctionne de manière similaire.
#Using the linear CV model from sklearn.linear_model import RidgeCV #Lasso Cross validation ridge_cv = RidgeCV(alphas = [0.0001, 0.001,0.01, 0.1, 1, 10]).fit(X_train, y_train) #score print("The train score for ridge model is {}".format(ridge_cv.score(X_train, y_train))) print("The train score for ridge model is {}".format(ridge_cv.score(X_test, y_test)))
Découvrez d'autres types de régression grâce à nos tutoriels sur la régression logistique en python et la régression linéaire en python.
Conclusion
Nous avons vu une mise en œuvre des modèles de régression ridge et lasso et les concepts théoriques et mathématiques qui sous-tendent ces techniques. Voici quelques-uns des principaux enseignements tirés de ce tutoriel :
- La fonction de coût pour la régression ridge et la régression lasso est similaire. Cependant, la régression ridge prend en compte le carré des coefficients et le lasso prend en compte la magnitude.
- La régression Lasso peut être utilisée pour la sélection automatique de caractéristiques, car la géométrie de sa région contrainte permet aux valeurs des coefficients d'être inertes à zéro.
- Une valeur alpha de zéro dans le modèle ridge ou lasso donnera des résultats similaires au modèle de régression.
- Plus la valeur alpha est importante, plus la pénalisation est agressive.
Vous pouvez trouver un carnet plus robuste et plus complet pour l'implémentation en Python ici, ou faire une plongée en profondeur dans les régressions avec notre cours Introduction à la régression en Python.