O que é uma matriz de confusão no aprendizado de máquina? Explicação da ferramenta de avaliação de modelos

Este ano foi um ano de inovação no campo da ciência de dados, com a inteligência artificial e o aprendizado de máquina dominando as manchetes. Embora não haja dúvidas sobre o progresso feito em 2023, é importante reconhecer que muitos desses avanços do aprendizado de máquina só foram possíveis graças aos processos de avaliação corretos pelos quais os modelos passam. Os profissionais de dados têm a tarefa de garantir que avaliações e processos precisos sejam realizados para medir o desempenho de um modelo de aprendizado de máquina. Isso não é benéfico, é essencial.

Se você deseja compreender a arte da ciência de dados, este artigo o guiará pelas etapas cruciais da avaliação de modelos usando a matriz de confusão, uma ferramenta relativamente simples, mas poderosa, amplamente usada na avaliação de modelos.

Então, vamos nos aprofundar e aprender mais sobre a matriz de confusão.

O que é a Matriz de Confusão?

A matriz de confusão é uma ferramenta usada para avaliar o desempenho de um modelo e é representada visualmente como uma tabela. Ele fornece uma camada mais profunda de informações aos profissionais de dados sobre o desempenho, os erros e os pontos fracos do modelo. Isso permite que os profissionais de dados analisem ainda mais seu modelo por meio de ajustes finos.

A estrutura da matriz de confusão

Vamos aprender sobre a estrutura básica de uma matriz de confusão, usando o exemplo da identificação de um e-mail como spam ou não spam.

• Verdadeiro positivo (TP) - Seu modelo previu a classe positiva. Por exemplo, identificar um e-mail de spam como spam.
• True Negative (TN) - Seu modelo previu corretamente a classe negativa. Por exemplo, identificar um e-mail normal como não sendo spam.
• Falso positivo (FP) - Seu modelo previu incorretamente a classe positiva. Por exemplo, identificar um e-mail normal como spam.
• Falso negativo (FN) - Seu modelo previu incorretamente a classe negativa. Por exemplo, identificar um e-mail de spam como um e-mail normal.

Para realmente entender o conceito de uma matriz de confusão, dê uma olhada na visualização abaixo:

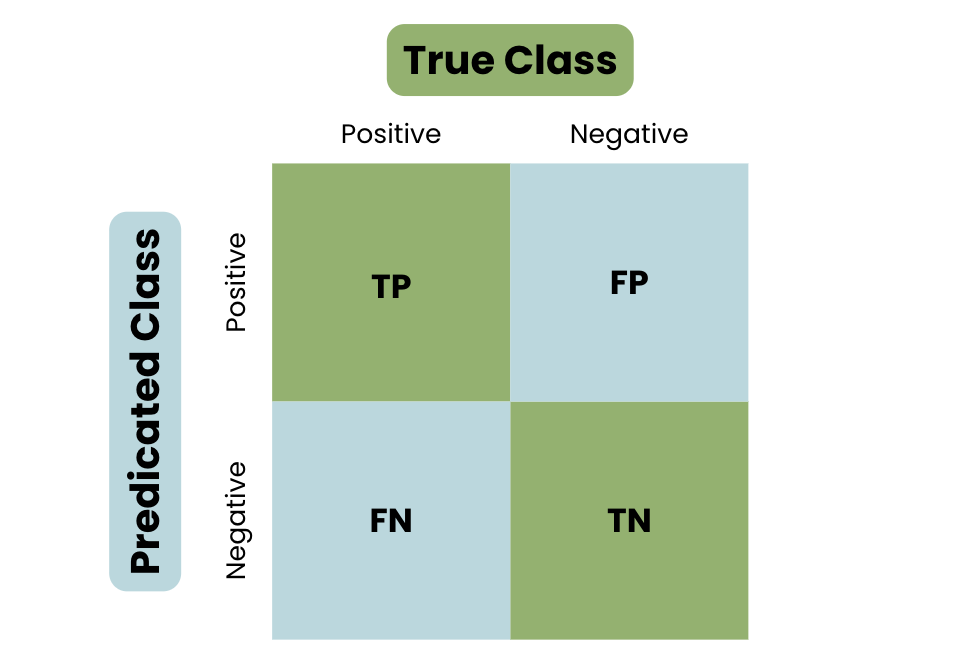
A estrutura básica de uma matriz de confusão

Terminologia da matriz de confusão

Para que você tenha uma compreensão aprofundada da Matriz de Confusão, é essencial entender as métricas importantes usadas para medir o desempenho de um modelo.

Vamos definir métricas importantes:

Precisão

A precisão mede o número total de classificações corretas dividido pelo número total de casos.

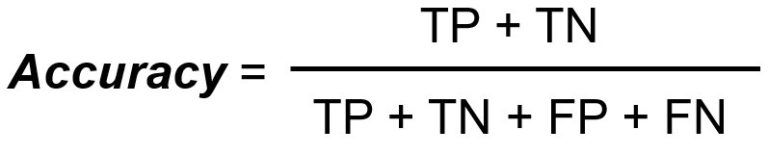
Recuperação/Sensibilidade

O Recall/Sensibilidade mede o número total de positivos verdadeiros dividido pelo número total de positivos reais.

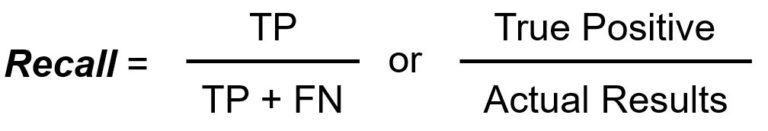
Precisão

A precisão mede o número total de positivos verdadeiros dividido pelo número total de positivos previstos.

Especificidade

A especificidade mede o número total de negativos verdadeiros dividido pelo número total de negativos reais.

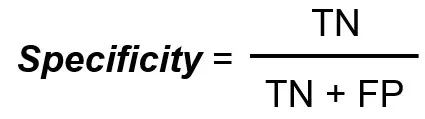
Pontuação da F1

A pontuação F1 é uma métrica única que é uma média harmônica de precisão e recuperação.

A função de uma matriz de confusão

Para compreender melhor a matriz de confusão, você deve entender o objetivo e por que ela é amplamente usada.

Quando se trata de medir o desempenho de um modelo ou de qualquer coisa em geral, as pessoas se concentram na precisão. No entanto, depender muito da métrica de precisão pode levar a decisões incorretas. Para entender isso, analisaremos as limitações do uso da precisão como uma métrica autônoma.

Limitações da precisão como uma métrica autônoma

Conforme definido acima, a precisão mede o número total de classificações corretas dividido pelo número total de casos. No entanto, o uso dessa métrica como autônoma tem limitações, como

• Trabalhando com dados desequilibrados: Nenhum dado é perfeito, e o uso da métrica de precisão deve ser avaliado em seu poder preditivo. Por exemplo, trabalhar com um conjunto de dados em que uma classe supera a outra fará com que o modelo atinja uma taxa de precisão mais alta, pois ele preverá a classe majoritária.
• Tipos de erro: Compreender e aprender sobre o desempenho do seu modelo em um contexto específico ajudará você a fazer o ajuste fino e melhorar o desempenho. Por exemplo, a diferenciação entre os tipos de erros por meio de uma matriz de confusão, como FP e FN, permitirá que você explore as limitações do modelo.

Devido a essas limitações, a matriz de confusão, juntamente com a variedade de métricas, oferece uma visão mais detalhada sobre como melhorar o desempenho de um modelo.

Os benefícios de uma matriz de confusão

Como visto na estrutura básica de uma matriz de confusão, as previsões são divididas em quatro categorias: Verdadeiro positivo, Verdadeiro negativo, Falso positivo e Falso negativo.

Essa análise detalhada oferece informações e soluções valiosas para melhorar o desempenho de um modelo:

• Solução de dados desequilibrados: Conforme explorado, o uso da precisão como uma métrica independente tem limitações quando se trata de dados desequilibrados. O uso de outras métricas, como precisão e recall, permite uma visão mais equilibrada e uma representação mais precisa. Por exemplo, falsos positivos e falsos negativos podem levar a grandes consequências em setores como o financeiro.
• Diferenciador de tipo de erro: A compreensão dos diferentes tipos de erros produzidos pelo modelo de aprendizado de máquina fornece conhecimento de suas limitações e áreas de aprimoramento.
• Compensações: A compensação entre o uso de diferentes métricas em uma Matriz de Confusão é essencial, pois elas afetam umas às outras. Por exemplo, um aumento na precisão normalmente leva a uma diminuição na recuperação. Isso orientará você a melhorar o desempenho do modelo usando o conhecimento dos valores métricos afetados.

Cálculo de uma matriz de confusão

Agora que temos um bom entendimento de uma matriz de confusão básica, sua terminologia e seu uso, vamos passar ao cálculo manual de uma matriz de confusão, seguido de um exemplo prático.

Cálculo manual de uma matriz de confusão

Aqui você encontra um guia passo a passo sobre como calcular manualmente uma Matriz de Confusão.

Definir os resultados

A primeira etapa será identificar os dois resultados possíveis de sua tarefa: Positivo ou negativo.

Coletando as previsões

Depois que os possíveis resultados forem definidos, a próxima etapa será coletar todas as previsões do modelo, inclusive quantas vezes o modelo previu cada classe e sua ocorrência.

Classificação dos resultados

Depois que todas as previsões tiverem sido coletadas, a próxima etapa é classificar os resultados em quatro categorias:

• Verdadeiro positivo (TP)
• Negativo verdadeiro (TN)
• Falso positivo (FP)
• Falso negativo (FN)

Criar uma matriz

Depois que os resultados forem classificados, a próxima etapa é apresentá-los em uma tabela de matriz, para serem analisados posteriormente usando uma variedade de métricas.

Exemplo prático de matriz de confusão

Vamos ver um exemplo prático para demonstrar esse processo.

Continuando a usar o mesmo exemplo de identificação de um e-mail como spam ou não spam, vamos criar um conjunto de dados hipotético em que spam é Positivo e não spam é Negativo. Temos os seguintes dados:

• Entre os 200 e-mails, 80 e-mails são realmente spam, e o modelo identifica corretamente 60 deles como spam (TP).
• Entre os 200 e-mails, 120 e-mails não são spam, e o modelo identifica corretamente 100 deles como não spam (TN).
• Entre os 200 e-mails, o modelo identifica incorretamente 20 e-mails não-spam como spam (FP).
• Entre os 200 e-mails, o modelo deixa passar 20 e-mails de spam e os identifica como não-spam (FN).

Neste ponto, definimos o resultado e coletamos os dados; a próxima etapa é classificar os resultados nas quatro categorias:

• Verdadeiro positivo: 60
• Verdadeiro negativo: 100
• Falso positivo: 20
• Falso negativo: 20

A próxima etapa é transformar isso em uma Matriz de Confusão:

Então, o que a Confusion Matrix nos diz?

• Os valores True Positives e True Negatives indicam previsões precisas.
• Os falsos positivos indicam que o modelo previu incorretamente a classe positiva.
• Os falsos negativos indicam que o modelo não conseguiu identificar e prever a classe positiva.

Usando essa matriz de confusão, podemos calcular as diferentes métricas: Exatidão, Recall/Sensibilidade, Precisão, Especificidade e Pontuação F1.

Saída de métricas da matriz de confusão

Precisão vs. precisão. Recall

Você pode estar se perguntando por que a pontuação F1 inclui precisão e recuperação em sua fórmula. A métrica de pontuação F1 é crucial ao lidar com dados desequilibrados ou quando você deseja equilibrar a troca entre precisão e recuperação.

A precisão mede a exatidão da previsão positiva. Ele responde à pergunta "quando o modelo previu VERDADEIRO, com que frequência ele estava certo?". A precisão, em particular, é importante quando o custo de um falso positivo é alto.

O recall ou a sensibilidade mede o número de positivos reais identificados corretamente pelo modelo. Ele responde à pergunta: "Quando a classe era realmente VERDADEIRA, com que frequência o classificador acertou?".

O recall é importante quando se demonstra que perder uma instância positiva (FN) é significativamente pior do que rotular incorretamente instâncias negativas como positivas.

• Uso de precisão: Os falsos positivos podem ter consequências graves. Por exemplo, um modelo de classificação usado no setor financeiro identificou erroneamente uma transação como fraudulenta. Em cenários como esse, a métrica de precisão é importante.
• Uso de recall: Identificar todos os casos positivos pode ser imperativo. Por exemplo, os modelos de classificação usados na área médica que não conseguem diagnosticar corretamente podem ser prejudiciais. Em cenários nos quais a identificação correta de todos os casos positivos é essencial, a métrica de recuperação é importante.

Matriz de confusão usando o Scikit-learn em Python

Para colocar isso em perspectiva, vamos criar uma matriz de confusão usando o Scikit-learn em Python, usando um classificador Random Forest.

A primeira etapa será importar as bibliotecas necessárias e criar seu conjunto de dados sintéticos.

# Import Libraries
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import confusion_matrix
import matplotlib.pyplot as plt
import seaborn as sns

# Synthetic Dataset
X, y = make_classification(n_samples=1000, n_features=20,
                           n_classes=2, random_state=42)

# Split into Training and Test Sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

A próxima etapa é treinar o modelo usando um classificador de floresta aleatória simples

# Train the Model
model = RandomForestClassifier(random_state=42)
model.fit(X_train, y_train)

Como fizemos com o exemplo prático, precisaremos classificar os resultados e transformá-los em uma matriz de confusão. Fazemos isso prevendo primeiro os dados de teste e, em seguida, gerando uma Matriz de Confusão:

# Predict on the Test Data
y_pred = model.predict(X_test)

# Generate the confusion matrix
cm = confusion_matrix(y_test, y_pred)

Agora, queremos gerar uma representação visual da matriz de confusão:

# Create a Confusion Matrix
plt.figure(figsize=(8, 8))
sns.heatmap(cm, annot=True, fmt='d', cmap='Greens')
plt.title('Confusion Matrix')
plt.ylabel('True label')
plt.xlabel('Predicted label')
plt.show()

Este é o resultado:

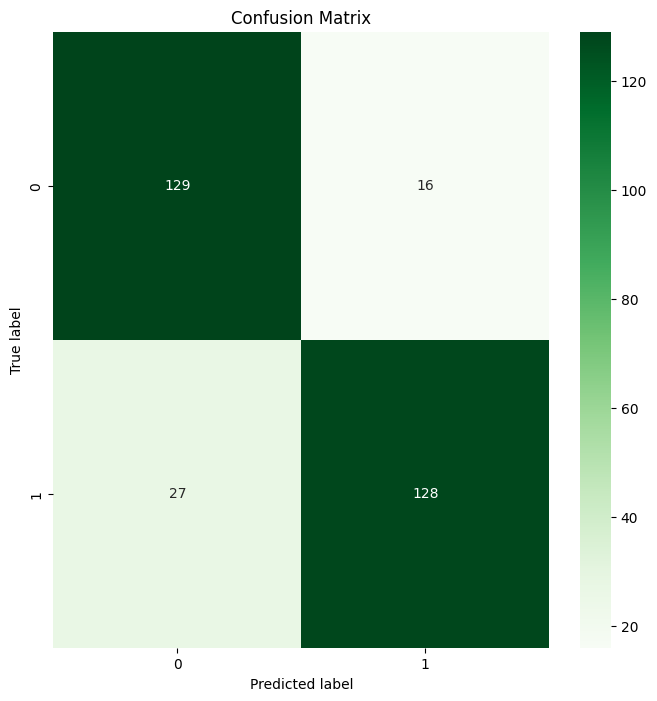
Saída da matriz de confusão do Random Forest

Tada 🎉 Você criou com sucesso sua primeira matriz de confusão usando o Scikit-learn!

Conclusão

Neste artigo, exploramos a definição de uma Matriz de Confusão, a terminologia importante que envolve a ferramenta de avaliação e as limitações e a importância das diferentes métricas. Poder calcular manualmente uma Matriz de Confusão é importante para sua base de conhecimento de ciência de dados, assim como poder executá-la usando bibliotecas como o Scikit-learn.

Se você quiser se aprofundar mais na Confusion Matrix, pratique as matrizes de confusão em R com Understanding Confusion Matrix in R. Aprofunde-se um pouco mais com nosso curso Model Validation in Python, no qual você aprenderá os fundamentos da validação de modelos, técnicas de validação e começará a criar modelos validados e de alto desempenho.