Score Z : Le guide complet de la normalisation statistique

Vous comparez les résultats au SAT de 2020 avec les résultats à l'ACT de la même année. Un étudiant a obtenu un score de 1200 au SAT tandis qu'un autre a obtenu un score de 24 à l'ACT. Quel résultat est le plus satisfaisant ? C'est précisément le problème que les scores z permettent de résoudre en convertissant différentes mesures en une échelle commune.

Les scores Z transforment les données brutes en valeurs normalisées, permettant ainsi d'effectuer des comparaisons significatives entre des distributions complètement différentes. Cette normalisation est utile lorsque vous analysez des données provenant de différentes sources, identifiez des valeurs aberrantes ou calculez des probabilités dans le cadre d'une analyse statistique. Nous aborderons les fondements mathématiques des scores z, nous examinerons étape par étape les méthodes de calcul pratiques et nous appliquerons ces techniques à différents scénarios. 

Qu'est-ce qu'un score Z ?

Les scores Z vous offrent un moyen standardisé de comprendre où se situe un point de données par rapport à sa distribution.

Définition et formule de base

Un score z représente le nombre d'écarts types d'un point de données par rapport à la moyenne de sa distribution. La formule est simple :

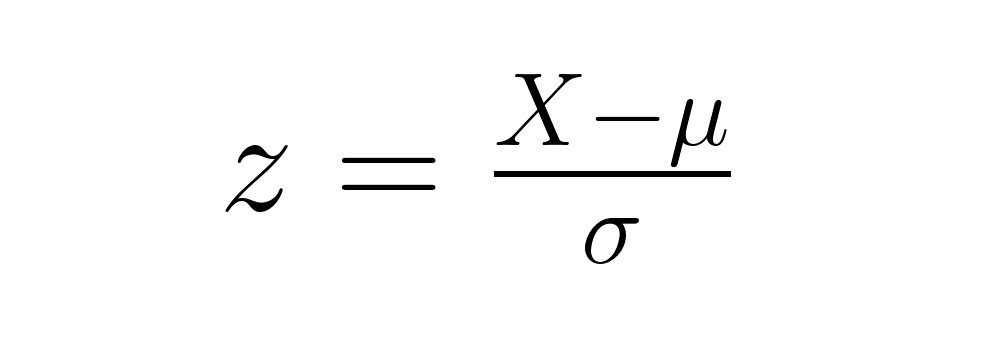
où X est votre score brut, μ (mu) est la moyenne de la population et σ (sigma) est l'écart type de la population. Les scores Z permettent de comparer directement des points de données provenant de différentes distributions, indépendamment de leurs unités ou échelles d'origine.

Propriétés de la distribution normale standard

Les scores Z transforment les données normalement distribuées en une distribution normale standard, qui est une courbe en cloche particulière avec une moyenne = 0 et un écart type = 1. Cette transformation permet d'obtenir des capacités analytiques utiles : environ 68 % des valeurs se situent dans un écart-type de la moyenne (scores Z compris entre -1 et +1), 95 % se situent dans deux écarts-types (-2 à +2) et 99,7 % se situent dans trois écarts-types (-3 à +3).

Formule et variations du score Z

La formule de base du score z fonctionne bien pour les données démographiques, mais l'analyse dans le monde réel nécessite souvent de légères modifications en fonction du type de données et de la taille de l'échantillon.

Formules standard du score z

Comme indiqué précédemment, la formule de base pour calculer un score z est la suivante : 

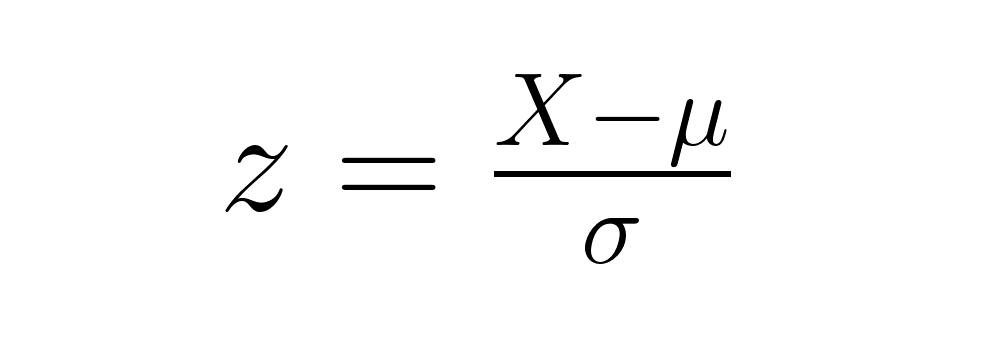
À partir de ce point de départ, des variations apparaissent selon que vous travaillez avec des données échantillonnées ou que vous testez une moyenne échantillonnée par rapport à une moyenne populationnelle. 

Pour les points de données individuels dans un échantillon : 

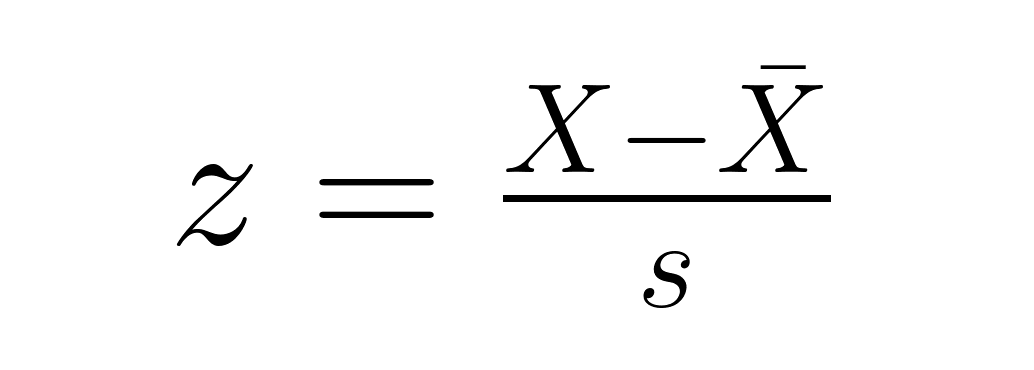
où X̄ est la moyenne de l'échantillon et s est l'écart type de l'échantillon (calculé avec le dé, le numérateur n−1). Cette version indique le nombre d'écarts-types d'un point par rapport à la moyenne de l'échantillon, ce qui est utile pour identifier les positions relatives et les valeurs aberrantes potentielles dans votre ensemble de données.

Lorsque nous vérifions si la moyenne d'un échantillon diffère significativement de la moyenne d'une population, nous utilisons l'erreur type de la moyenne dans notre calcul :

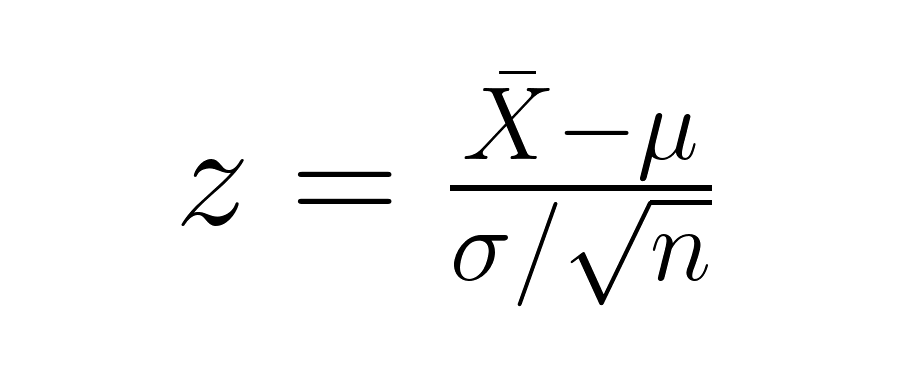
où X̄ est la moyenne de votre échantillon, μ est la moyenne de la population, σ est l'écart type de la population et n est la taille de votre échantillon. Le dénominateur (σ/√n) représente l'erreur type de la moyenne, qui tient compte de la taille de l'échantillon dans le test d'hypothèse.

Calculer un score brut à partir d'un score z

Il arrive parfois que l'on procède à l'inverse à partir des scores z pour déterminer les valeurs initiales. En réorganisant la formule, on obtient : 

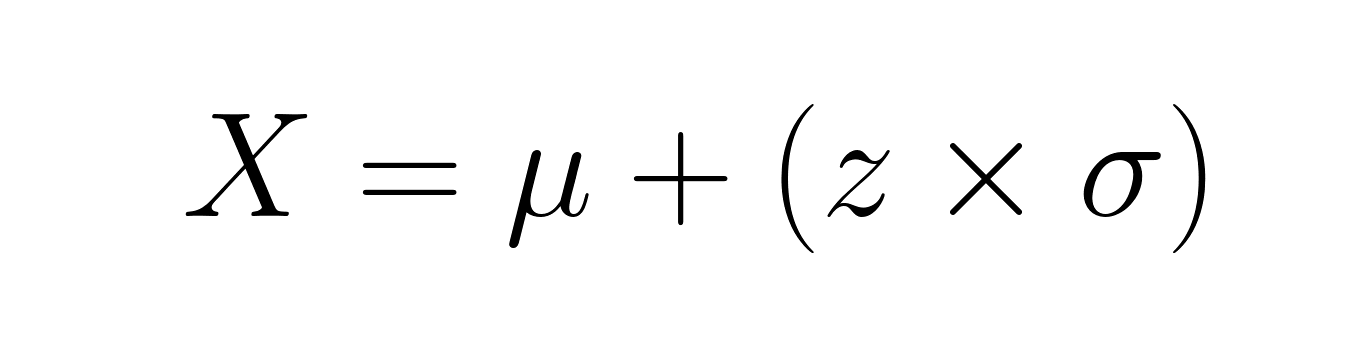
Si le résultat d'un élève à un examen présente un score z de 1,5, avec une moyenne de 75 et un écart type de 10, son résultat réel sera de 75 + (1,5 × 10) = 90.

Comment calculer un score Z

La conversion des données brutes en scores z implique un processus systématique qui devient naturel avec la pratique.

Calcul étape par étape

Voici comment calculer manuellement les scores z : Tout d'abord, déterminez la moyenne de votre distribution en additionnant toutes les valeurs et en divisant par le nombre total. Ensuite, veuillez calculer l'écart type en déterminant la racine carrée de la moyenne des différences au carré par rapport à la moyenne. Enfin, appliquez la formule du score z en soustrayant la moyenne de votre score brut et en divisant par l'écart type.

Examinons un exemple : Si les notes d'examen 85, 92, 78, 96, 88 représentent l'ensemble de nos données (moyenne = 87,8, écart type = 6,14), une note de 92 a un score z de (92 - 87,8) / 6,14 = 0,68.

Vous pouvez également calculer rapidement les scores z à l'aide de la fonction Excel « STANDARDIZE() » ou de la même fonction dans Google Sheets, en combinaison avec AVERAGE() et STDEV.P() pour les données de population ou STDEV.S() pour les données d'échantillon.

Directives d'interprétation

L'interprétation du score Z suit des règles directionnelles cohérentes, quelles que soient vos données d'origine. Les scores z positifs indiquent des valeurs supérieures à la moyenne, tandis que les scores z négatifs indiquent des valeurs inférieures à la moyenne. Un score z de 0 indique que votre point de données correspond exactement à la moyenne.

Pour les données normalement distribuées, vous pouvez appliquer des directives d'interprétation supplémentaires : les valeurs dont les scores z sont supérieurs à ±2 sont inhabituelles (elles surviennent dans environ 5 % des cas), tandis que les scores z supérieurs à ±3 sont rares (probabilité inférieure à 1 %). Vous pouvez déterminer les centiles exacts pour les distributions normales à l'aide des tableaux z, qui indiquent le pourcentage d'observations inférieures à un score z donné.

Pour les données non normales, les scores z indiquent toujours la position relative et aident à identifier les valeurs aberrantes potentielles, mais les pourcentages spécifiques ne s'appliquent pas.

Interprétation des scores Z et de l'écart type

Comprendre la relation entre les scores z et l'écart type vous aide à saisir ce que ces valeurs normalisées représentent réellement.

Relation avec l'écart type

Les scores Z mesurent directement la distance par rapport à la moyenne en unités d'écart type. Un score z de 2,5 signifie que votre point de données se situe à 2,5 écarts-types au-dessus de la moyenne. Cela diffère de l'écart type lui-même, qui mesure la dispersion typique des données autour de la moyenne.

L'écart type décrit la variabilité au sein d'un même ensemble de données, tandis que les scores z permettent de comparer différents ensembles de données ayant des moyennes et des écarts différents. Considérez l'écart type comme une mesure de la « largeur » de votre distribution, tandis que les scores z vous indiquent précisément où se situent les points individuels dans cette largeur.

Pourcentage d'observations inférieures à un score z

Pour les données normalement distribuées, les tableaux z convertissent les scores z en rangs centiles, indiquant ainsi le pourcentage d'observations inférieures à votre valeur. Dans une distribution normale, un score z de 1,0 correspond au 84e centile, ce qui signifie que 84 % des observations sont inférieures.

Les calculatrices en ligne et les logiciels statistiques modernes permettent d'effectuer ces conversions instantanément pour les distributions normales. Cependant, pour les données non normales, il est nécessaire d'utiliser des méthodes spécifiques à la distribution pour déterminer les centiles, car les pourcentages standard de la table z ne s'appliquent pas.

Applications des scores Z

Les scores Z apparaissent dans les statistiques et la science des données, permettant de résoudre des problèmes pratiques dans divers domaines.

Estimation de probabilité et test d'hypothèse

Les scores Z constituent la base des calculs de probabilité dans les distributions normales. Lorsque vous souhaitez déterminer la probabilité d'obtenir une note supérieure à 600 dans un examen à distribution normale avec une moyenne de 500 et un écart type de 100, vous devez d'abord convertir 600 en un score z de 1,0, puis rechercher la probabilité correspondante (environ 16 %). Vous pouvez également calculer les probabilités entre deux scores z en déterminant la différence entre leurs probabilités cumulées.

Dans le cadre des tests d'hypothèse, les scores z permettent de déterminer la signification statistique en comparant les statistiques d'échantillon aux valeurs attendues de la population, ensupposant une distribution normale. Notre cours « Hypothesis Testing in R » (Tests d'hypothèses dans R) aborde ces applications et montre comment les scores z sont liés aux valeurs p et aux intervalles de confiance. 

Détection des valeurs aberrantes et normalisation des données

Les scientifiques des données utilisent régulièrement les scores z pour identifier les valeurs aberrantes potentielles. Pour les données normalement distribuées, les valeurs dont les scores z dépassent ±3 sont très inhabituelles (elles surviennent moins de 1 % du temps) et indiquent souvent des erreurs de saisie, des problèmes de mesure ou des cas véritablement exceptionnels qui méritent d'être examinés. Même avec des données non normales, les scores z extrêmes peuvent signaler des observations qui méritent un examen plus approfondi.

La normalisation de l'ensemble des données à l'aide de scores z crée des variables dont la moyenne est égale à 0 et l'écart type à 1, ce qui les rend directement comparables. Cela s'avère utile dans les algorithmes d'apprentissage automatique sensibles aux différences d'échelle, tels que le clustering k-means ou les réseaux neuronaux. 

Comparaison des scores sur différentes échelles

Les scores Z permettent d'effectuer des comparaisons équitables entre différents tests ou mesures présentant des distributions similaires. La comparaison entre le SAT et l'ACT devient plus claire une fois que vous convertissez les deux scores en scores z à l'aide de leurs moyennes et écarts-types respectifs. Un étudiant ayant obtenu un score z de 1,2 au SAT a surpassé un étudiant ayant obtenu un score z de 0,8 à l'ACT, malgré les différences d'échelle.

Applications avancées en statistiques et science des données

Les scores Z apparaissent dans des techniques analytiques sophistiquées telles que l'analyse par grappes (où la normalisation garantit que toutes les variables contribuent de manière égale), la mise à l'échelle multidimensionnelle et l'analyse en composantes principales. 

Dans l'analyse de régression, les coefficients standardisés (également appelés coefficients bêta) permettent de comparer l'importance relative des prédicteurs continus en les plaçant sur la même échelle. Le processus consiste à convertir toutes les variables (prédictives et résultats) en scores z avant d'effectuer la régression. Les coefficients standardisés obtenus indiquent « de combien d'écarts-types le résultat devrait-il varier lorsque ce prédicteur augmente d'un écart-type », ce qui permet d'effectuer des comparaisons directes entre des prédicteurs ayant des unités d'origine différentes.

Évaluation des soins de santé et de l'éducation

Les professionnels de santé utilisent les scores z pour interpréter les résultats des tests en les comparant aux données de référence de la population. Les scores z de densité osseuse comparent les mesures individuelles à celles de personnes du même âge, ce qui facilite le diagnostic de maladies telles que l'ostéoporose. Les évaluations éducatives s'appuient sur les scores z pour normaliser les résultats des tests entre différentes années et populations, ce qui permet des comparaisons équitables malgré des conditions de test variables. 

Méthodes et outils informatiques

L'analyse moderne s'appuie sur des outils logiciels qui automatisent les calculs des scores z.

Tableaux Z et conversion en centiles

Les tableaux Z traditionnels restent utiles pour comprendre le lien entre les scores Z et les probabilités dans les distributions normales. Ces tableaux présentent les probabilités cumulées pour les valeurs de la distribution normale standard, généralement comprises entre z = -3,49 et z = 3,49. Pour consulter un tableau z, identifiez les deux premiers chiffres de votre score z dans la colonne de gauche, puis localisez le troisième chiffre dans la ligne supérieure.

Utilisation de la programmation pour calculer les scores z

Nous avons abordé la fonction Excel « STANDARDIZE() » précédemment dans la section consacrée au calcul étape par étape. Pour Python et R, examinons le même exemple en utilisant les notes d'examen : 85, 92, 78, 96, 88.

Python avec scipy.stats :

import numpy as np
from scipy import stats

# Our exam scores
scores = np.array([85, 92, 78, 96, 88])

# Calculate z-scores using scipy (uses population std by default)
# This means dividing by N, not N-1
z_scores = stats.zscore(scores)
print(f"Z-scores: {z_scores}")
# Output: [-0.46  0.68 -1.59  1.33  0.03]

# Manual calculation for verification
mean_score = np.mean(scores)
std_score = np.std(scores, ddof=0)  # Population standard deviation
z_manual = (scores - mean_score) / std_score
print(f"Manual z-scores: {z_manual}")

R à l'aide de la fonction scale() :

# Our exam scores
scores <- c(85, 92, 78, 96, 88)

# Calculate z-scores using scale() (uses sample std by default)
z_scores <- scale(scores)[,1]  # Extract vector from matrix
print(paste("Z-scores:", z_scores))
# Output: [-0.41  0.61 -1.43  1.19  0.03]

# Manual calculation for verification
z_manual <- (scores - mean(scores)) / sd(scores)
print(paste("Manual z-scores:", z_manual))

Veuillez noter que Python et R fournissent des résultats légèrement différents, car scipy.stats.zscore() utilise l'écart type de la population (division par N), tandis que R utilise scale() l'écart type de l'échantillon (division par N-1). Pour notre score de 92, Python donne un score z de 0,68 tandis que R donne 0,61. Les deux sont corrects selon que vous considérez vos données comme une population complète ou un échantillon. 

Conclusion

Les scores Z constituent un pont entre les données brutes et une interprétation statistique significative. Ils permettent d'effectuer des comparaisons équitables à différentes échelles, facilitent les calculs de probabilité lorsque les données suivent une distribution normale et aident à identifier les observations inhabituelles qui méritent d'être examinées.

Ces valeurs standardisées s'étendent de l'analyse de données de base aux applications avancées d'apprentissage automatique, ce qui en fait des outils utiles pour toute personne travaillant avec des données quantitatives. Nous vous invitons à explorer notre cours « Inférence pour les données numériques dans R » afin de découvrir les techniques d'inférence statistique à l'aide d'ensembles de données réels, ainsi que notre cours « Tests A/B dans R » pour les méthodes de test d'hypothèses où les concepts de score z sont fréquemment appliqués.