Pontuação Z: O Guia Completo para Padronização Estatística

Você está comparando as notas do SAT de 2020 com as notas do ACT do mesmo ano. Um aluno tirou 1200 no SAT, enquanto outro tirou 24 no ACT, mas qual desempenho é melhor? Esse é exatamente o problema que os escores z resolvem, convertendo diferentes medidas para uma escala comum.

Os escores Z transformam dados brutos em valores padronizados, possibilitando comparações significativas entre distribuições completamente diferentes. Essa padronização ajuda quando você está analisando dados de diferentes fontes, identificando valores atípicos ou calculando probabilidades em análises estatísticas. Vamos falar sobre os fundamentos matemáticos por trás dos escores z, ver métodos práticos de cálculo passo a passo e aplicar essas técnicas em diferentes situações. 

O que é um Z-Score?

Os escores Z oferecem uma maneira padronizada de entender onde qualquer ponto de dados se situa em relação à sua distribuição.

Definição e fórmula principal

Um z-score mostra quantos desvios padrão um ponto de dados está longe da média da sua distribuição. A fórmula é simples:

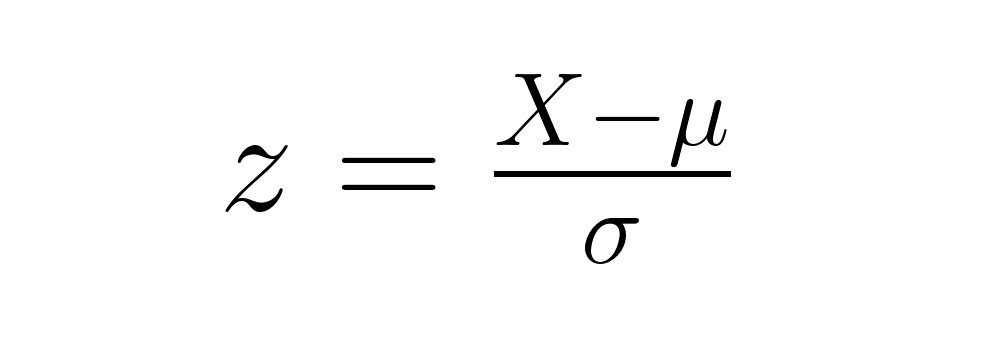
onde X é a sua pontuação bruta, μ (mu) é a média da população e σ (sigma) é o desvio padrão da população. Os escores Z permitem comparar diretamente pontos de dados de diferentes distribuições, independentemente de suas unidades ou escalas originais.

Propriedades da distribuição normal padrão

Os escores Z transformam dados normalmente distribuídos na distribuição normal padrão, que é uma curva em forma de sino especial com média = 0 e desvio padrão = 1. Essa transformação abre algumas possibilidades analíticas bem úteis: cerca de 68% dos valores ficam dentro de um desvio padrão da média (pontuações Z entre -1 e +1), 95% ficam dentro de dois desvios padrão (-2 a +2) e 99,7% ficam dentro de três desvios padrão (-3 a +3).

Fórmula e variações do Z-Score

A fórmula básica do z-score funciona bem para dados populacionais, mas a análise do mundo real muitas vezes precisa de pequenas mudanças, dependendo do tipo de dados e do tamanho da amostra.

Fórmulas padrão para o z-score

Como falamos antes, a fórmula básica para o z-score é: 

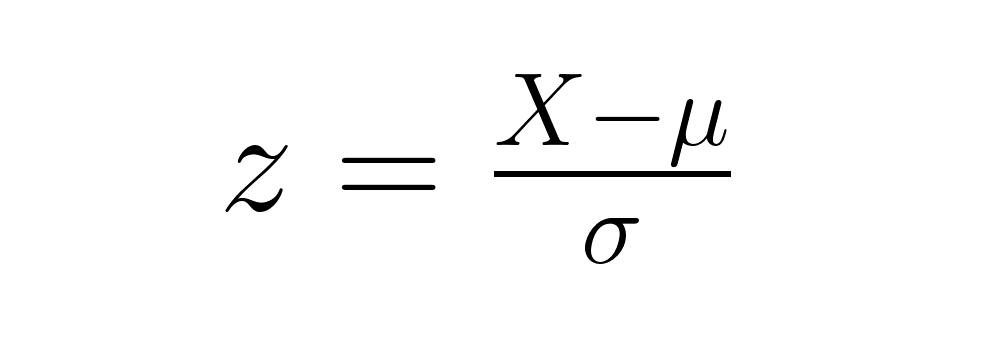
A partir desse ponto, surgem variações dependendo se você está trabalhando com dados de amostra ou testando uma média amostral em relação a uma média populacional. 

Para pontos de dados individuais em uma amostra: 

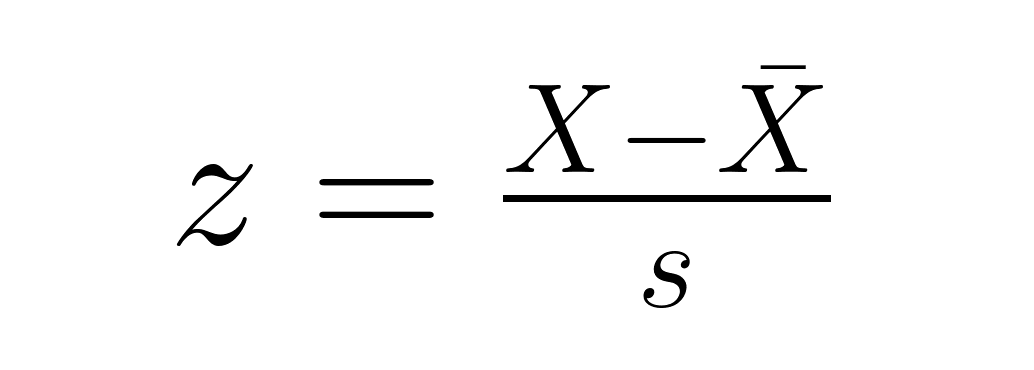
onde X̄ é a média amostral e s é o desvio padrão amostral (calculado com o denominador dee n−1). Essa versão mostra quantos desvios padrão amostrais um ponto está da média amostral, o que é útil para identificar posições relativas e possíveis outliers dentro do seu conjunto de dados.

Quando a gente quer saber se a média de uma amostra é bem diferente da média de uma população, a gente usa o erro padrão da média no cálculo:

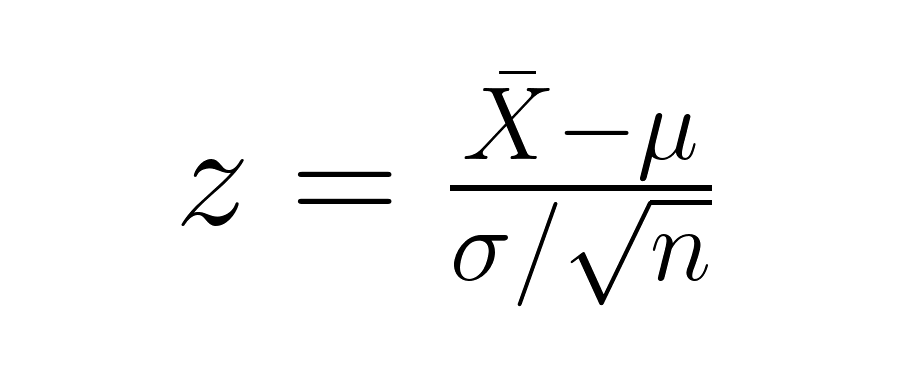
onde X̄ é a média da sua amostra, μ é a média da população, σ é o desvio padrão da população e n é o tamanho da sua amostra. O denominador (σ/√n) representa o erro padrão da média, que leva em conta o tamanho da amostra nos testes de hipóteses.

Calculando uma pontuação bruta a partir de uma pontuação z

Às vezes, você trabalha de trás para frente a partir das pontuações z para encontrar os valores originais. Reorganizando a fórmula, você obtém: 

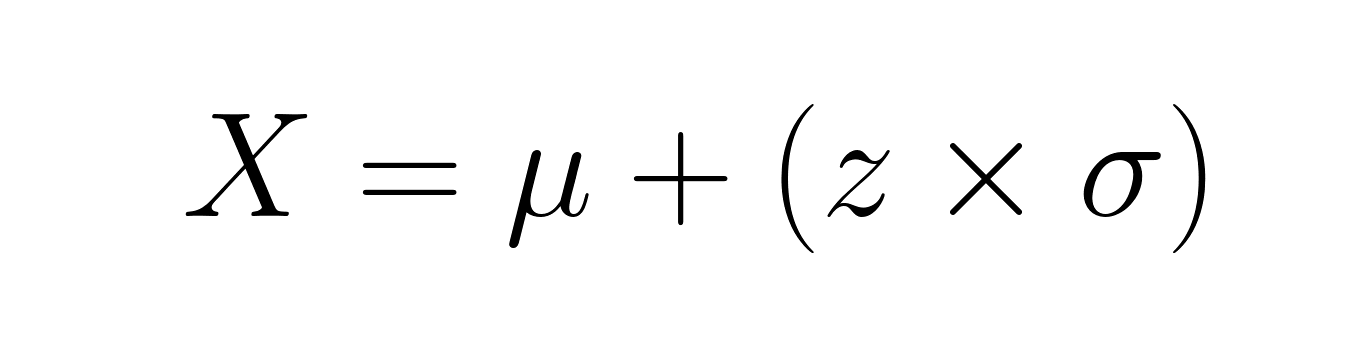
Se a nota de um aluno tiver um z-score de 1,5 em uma prova com média 75 e desvio padrão 10, a nota real dele seria 75 + (1,5 × 10) = 90.

Como calcular um Z-Score

Converter dados brutos em escores z envolve um processo sistemático que, com a prática, vira algo natural.

Cálculo passo a passo

Veja como calcular os escores z manualmente: Primeiro, calcule a média da sua distribuição somando todos os valores e dividindo pelo número total. Depois, calcule o desvio padrão achando a raiz quadrada da média das diferenças quadradas em relação à média. Por fim, use a fórmula do z-score tirando a média da sua pontuação bruta e dividindo pelo desvio padrão.

Vamos ver um exemplo: Se as notas dos exames 85, 92, 78, 96, 88 representam nosso conjunto de dados completo (média = 87,8, desvio padrão = 6,14), uma nota de 92 tem uma pontuação z de (92 - 87,8) / 6,14 = 0,68.

Você também pode calcular rapidamente os escores z usando a função STANDARDIZE() do Excel ou a mesma função no Google Sheets, junto com AVERAGE() e STDEV.P() para dados populacionais ou STDEV.S() para dados amostrais.

Diretrizes de interpretação

A interpretação do Z-score segue regras direcionais consistentes, independentemente dos seus dados originais. Pontuações z positivas indicam valores acima da média, enquanto pontuações z negativas mostram valores abaixo da média. Um z-score de 0 quer dizer que o seu ponto de dados é igual à média.

Para dados normalmente distribuídos, você pode usar algumas dicas extras de interpretação: valores com pontuações z além de ±2 são incomuns (acontecem em cerca de 5% dos casos), enquanto pontuações z além de ±3 são raras (menos de 1% de probabilidade). Você pode encontrar os percentis exatos para distribuições normais usando tabelas z, que mostram qual porcentagem das observações fica abaixo de qualquer pontuação z dada.

Para dados não normais, os escores z ainda mostram a posição relativa e ajudam a identificar possíveis valores atípicos, mas as porcentagens específicas não se aplicam.

Interpretando pontuações Z e desvio padrão

Entender a relação entre os escores z e o desvio padrão ajuda a compreender o que esses valores padronizados realmente representam.

Relação com o desvio padrão

Os escores Z medem diretamente a distância da média em unidades de desvio padrão. Um z-score de 2,5 quer dizer que seu ponto de dados está 2,5 desvios padrão acima da média. Isso é diferente do desvio padrão em si, que mede a dispersão típica dos dados em torno da média.

O desvio padrão mostra como os dados variam dentro de um único conjunto, enquanto os escores z permitem comparar diferentes conjuntos de dados com médias e dispersões diferentes. Pense no desvio padrão como uma medida da “largura” da sua distribuição, enquanto os escores z mostram exatamente onde cada ponto se encaixa nessa largura.

Porcentagem de observações abaixo de um escore z

Para dados normalmente distribuídos, as tabelas z convertem os escores z em classificações percentuais, mostrando qual porcentagem das observações fica abaixo do seu valor. Em uma distribuição normal, um escore z de 1,0 é igual ao percentil 84, ou seja, 84% das observações são menores.

As calculadoras online modernas e os softwares estatísticos fazem essas conversões rapidinho para distribuições normais. Mas, para dados que não são normais, você vai precisar de métodos específicos de distribuição para calcular os percentis, já que as porcentagens padrão da tabela z não vão funcionar.

Aplicações dos escores Z

Os escores Z aparecem em toda a estatística e ciência de dados, resolvendo problemas práticos em diversos campos.

Estimativa de probabilidade e teste de hipóteses

Os escores Z são a base dos cálculos de probabilidade nas distribuições normais. Quando você quer saber a chance de tirar mais de 600 em uma prova com distribuição normal, média de 500 e desvio padrão de 100, primeiro você transforma 600 em um z-score de 1,0 e depois procura a probabilidade correspondente (cerca de 16%). Você também pode calcular as probabilidades entre dois escores z encontrando a diferença entre suas probabilidades cumulativas.

Nos testes de hipóteses, os escores z ajudam a determinar a significância estatística comparando as estatísticas da amostra com os valores esperados da população, partindo doprincípio de que tudo está normal. Nosso curso Teste de Hipóteses em R fala sobre essas aplicações, mostrando como os escores z se conectam aos valores p e aos intervalos de confiança. 

Detecção de valores atípicos e padronização de dados

Os cientistas de dados costumam usar escores z para identificar possíveis valores atípicos. Para dados normalmente distribuídos, valores com pontuações z além de ±3 são bem incomuns (ocorrem menos de 1% das vezes) e geralmente indicam erros de entrada de dados, problemas de medição ou casos realmente excepcionais que valem a pena investigar. Mesmo com dados não normais, os escores z extremos podem sinalizar observações que merecem uma análise mais detalhada.

Padronizar conjuntos de dados inteiros com escores z cria variáveis com média 0 e desvio padrão 1, tornando-as diretamente comparáveis. Isso é super útil em algoritmos de machine learning que são sensíveis a diferenças de escala, como agrupamento k-means ou redes neurais. 

Comparando pontuações em diferentes escalas

Os escores Z permitem comparações justas entre diferentes testes ou medições com formas de distribuição parecidas. Essa comparação anterior entre o SAT e o ACT fica mais fácil quando você converte as duas notas em notas z usando as respectivas médias e desvios padrão. Um aluno com pontuação z no SAT de 1,2 teve um desempenho melhor do que alguém com pontuação z no ACT de 0,8, mesmo com as diferentes escalas.

Aplicações avançadas em estatística e ciência de dados

Os escores Z aparecem em técnicas analíticas sofisticadas, como análise de agrupamentos (onde a padronização garante que todas as variáveis contribuam igualmente), escalonamento multidimensional e análise de componentes principais. 

Na análise de regressão, os coeficientes padronizados (também chamados de coeficientes beta) ajudam a comparar a importância relativa dos preditores contínuos, colocando-os na mesma escala. O processo envolve converter todas as variáveis (tanto preditoras quanto resultados) em escores z antes de fazer a regressão. Os coeficientes padronizados resultantes indicam “quantos desvios padrão se espera que o resultado mude quando esse preditor aumenta em um desvio padrão?”, tornando possível fazer comparações diretas entre preditores com unidades originais diferentes.

Avaliação de saúde e educação

Os profissionais médicos usam os escores z para interpretar os resultados dos testes, comparando-os com os dados da população de referência. Os escores z da densidade óssea comparam as medições individuais com as de pessoas da mesma idade, ajudando a diagnosticar condições como a osteoporose. As avaliações educacionais usam notas z para padronizar os resultados dos testes em diferentes anos e populações, permitindo comparações justas mesmo com condições de teste diferentes. 

Métodos e ferramentas computacionais

A análise moderna depende de ferramentas de software que automatizam os cálculos do z-score.

Tabelas Z e conversão percentual

As tabelas Z tradicionais continuam sendo úteis para entender a relação entre os escores Z e as probabilidades nas distribuições normais. Essas tabelas mostram as probabilidades acumuladas para valores da distribuição normal padrão, que geralmente vão de z = -3,49 a z = 3,49. Para ler uma tabela z, encontre os dois primeiros dígitos da sua pontuação z na coluna da esquerda e, em seguida, localize o terceiro dígito na linha superior.

Usando programação para calcular escores z

A gente já falou sobre a função “ STANDARDIZE() ” do Excel antes, na seção de cálculos passo a passo. Para Python e R, vamos trabalhar com o mesmo exemplo usando notas de exames: 85, 92, 78, 96, 88.

Python com scipy.stats:

import numpy as np
from scipy import stats

# Our exam scores
scores = np.array([85, 92, 78, 96, 88])

# Calculate z-scores using scipy (uses population std by default)
# This means dividing by N, not N-1
z_scores = stats.zscore(scores)
print(f"Z-scores: {z_scores}")
# Output: [-0.46  0.68 -1.59  1.33  0.03]

# Manual calculation for verification
mean_score = np.mean(scores)
std_score = np.std(scores, ddof=0)  # Population standard deviation
z_manual = (scores - mean_score) / std_score
print(f"Manual z-scores: {z_manual}")

R usando a função scale():

# Our exam scores
scores <- c(85, 92, 78, 96, 88)

# Calculate z-scores using scale() (uses sample std by default)
z_scores <- scale(scores)[,1]  # Extract vector from matrix
print(paste("Z-scores:", z_scores))
# Output: [-0.41  0.61 -1.43  1.19  0.03]

# Manual calculation for verification
z_manual <- (scores - mean(scores)) / sd(scores)
print(paste("Manual z-scores:", z_manual))

Observe que o Python e o R apresentam resultados ligeiramente diferentes porque scipy.stats.zscore() usa o desvio padrão da população (dividindo por N), enquanto o R usa scale() o desvio padrão da amostra (dividindo por N-1). Para nossa pontuação de 92, o Python dá uma pontuação z de 0,68, enquanto o R dá 0,61. Ambos estão corretos, dependendo se você está tratando seus dados como uma população completa ou uma amostra. 

Conclusão

Os escores Z fazem a ponte entre os dados brutos e uma interpretação estatística que faz sentido. Elas permitem comparações justas entre diferentes escalas, ajudam nos cálculos de probabilidade quando os dados seguem distribuições normais e ajudam a identificar observações incomuns que merecem ser investigadas.

Esses valores padronizados vão desde a análise básica de dados até aplicações avançadas de machine learning, tornando-os ferramentas úteis para qualquer pessoa que trabalhe com dados quantitativos. Dá uma olhada no nosso curso Inferência para Dados Numéricos em R pra ver técnicas de inferência estatística com conjuntos de dados reais, e no nosso curso Testes A/B em R pra métodos de teste de hipóteses onde os conceitos de z-score são bem usados.