Puntuación Z: La guía completa para la estandarización estadística

Estás comparando las puntuaciones del SAT de 2020 con las puntuaciones del ACT del mismo año. Un estudiante obtuvo una puntuación de 1200 en el SAT, mientras que otro obtuvo una puntuación de 24 en el ACT, pero ¿qué resultado es mejor? Este es precisamente el problema que resuelven las puntuaciones z al convertir diferentes medidas a una escala común.

Las puntuaciones Z transforman los datos brutos en valores estandarizados, lo que permite realizar comparaciones significativas entre distribuciones completamente diferentes. Esta estandarización resulta útil a la hora de analizar datos procedentes de diferentes fuentes, identificar valores atípicos o calcular probabilidades en análisis estadísticos. Cubriremos los fundamentos matemáticos detrás de las puntuaciones z, trabajaremos paso a paso con métodos de cálculo prácticos y aplicaremos estas técnicas a diferentes escenarios. 

¿Qué es una puntuación Z?

Las puntuaciones Z te ofrecen una forma estandarizada de comprender dónde se sitúa cualquier punto de datos en relación con su distribución.

Definición y fórmula básica

Una puntuación z representa el número de desviaciones estándar que un punto de datos se aleja de la media de su distribución. La fórmula es sencilla:

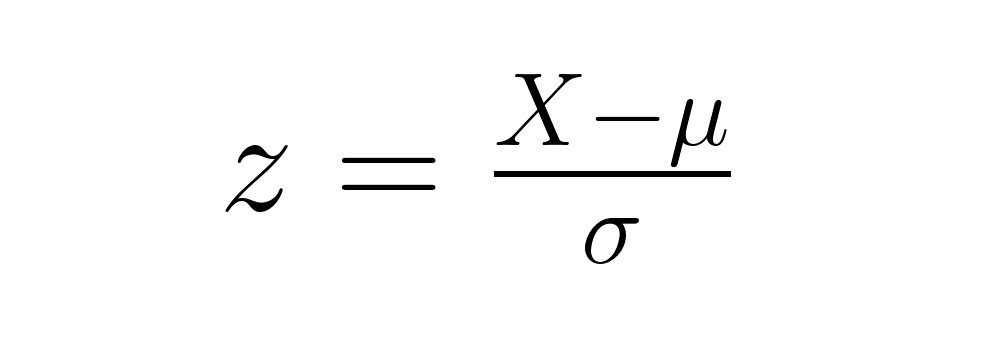
donde X es tu puntuación bruta, μ (mu) es la media poblacional y σ (sigma) es la desviación estándar poblacional. Las puntuaciones Z permiten comparar directamente puntos de datos de diferentes distribuciones, independientemente de sus unidades o escalas originales.

Propiedades de la distribución normal estándar

Las puntuaciones Z transforman los datos distribuidos normalmente en la distribución normal estándar, que es una curva de campana especial con media = 0 y desviación estándar = 1. Esta transformación permite acceder a algunas capacidades analíticas útiles: aproximadamente el 68 % de los valores se encuentran dentro de una desviación estándar de la media (puntuaciones Z entre -1 y +1), el 95 % se encuentran dentro de dos desviaciones estándar (-2 a +2) y el 99,7 % se encuentran dentro de tres desviaciones estándar (-3 a +3).

Fórmula y variaciones de la puntuación Z

La fórmula básica de la puntuación z funciona bien para los datos poblacionales, pero el análisis del mundo real a menudo requiere ligeras modificaciones en función del tipo de datos y el tamaño de la muestra.

Fórmulas estándar para el cálculo de la puntuación z

Como se ha mencionado anteriormente, la fórmula básica para calcular la puntuación z es: 

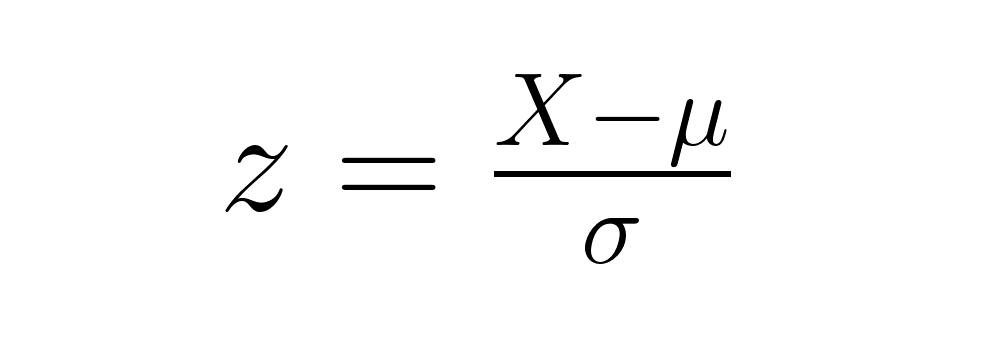
A partir de este punto de partida, surgen variaciones dependiendo de si se trabaja con datos muestrales o se compara una media muestral con una media poblacional. 

Para puntos de datos individuales en una muestra: 

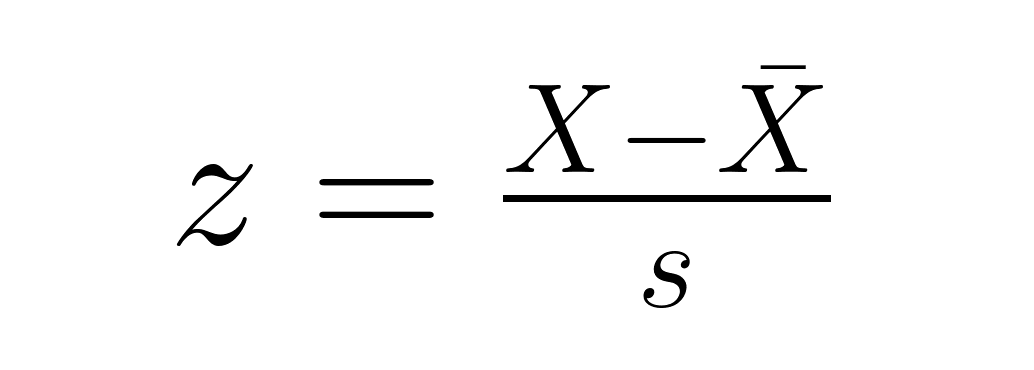
donde X̄ es la media muestral y s es la desviación estándar muestral (calculada con el denominador den−1). Esta versión muestra cuántas desviaciones estándar de la muestra se encuentra un punto respecto a la media de la muestra, lo que resulta útil para identificar posiciones relativas y posibles valores atípicos dentro del conjunto de datos.

Cuando se comprueba si la media de una muestra difiere significativamente de la media de una población, utilizamos el error estándar de la media en nuestro cálculo:

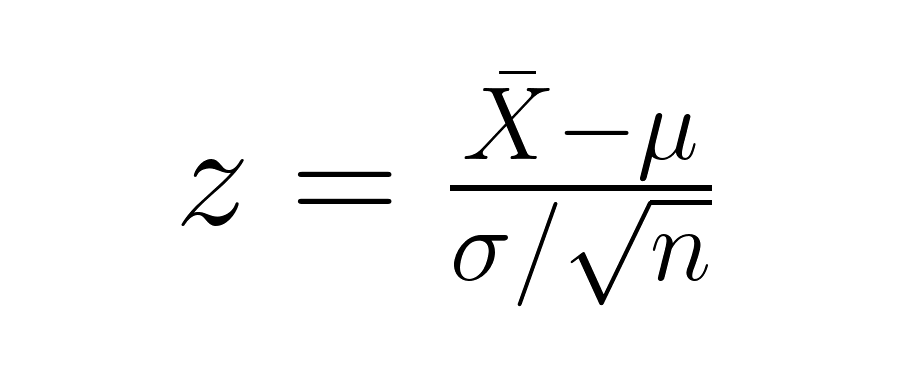
donde X̄ es la media muestral, μ es la media poblacional, σ es la desviación estándar poblacional y n es el tamaño de la muestra. El denominador (σ/√n) representa el error estándar de la media, que tiene en cuenta el tamaño de la muestra en la comprobación de hipótesis.

Cálculo de una puntuación bruta a partir de una puntuación z

A veces se trabaja hacia atrás a partir de las puntuaciones z para encontrar los valores originales. Reorganizando la fórmula se obtiene: 

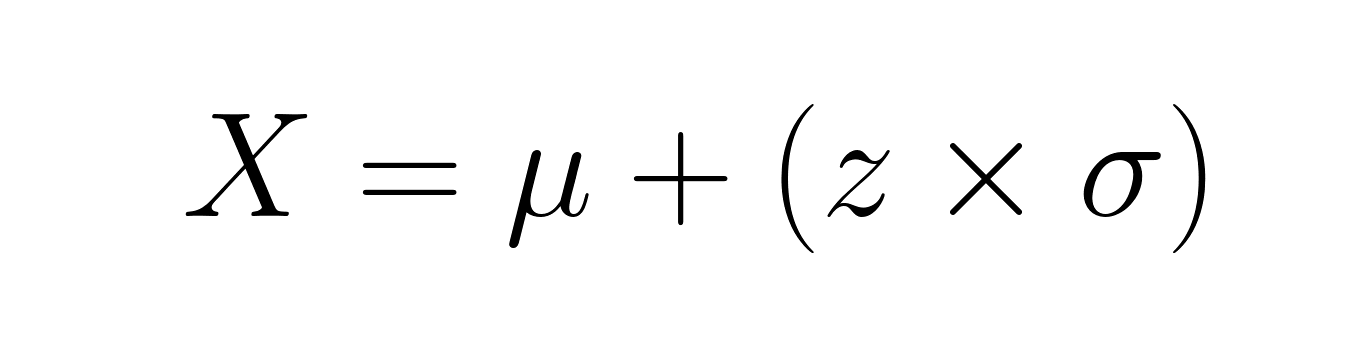
Si la puntuación de un estudiante en un examen tiene una puntuación z de 1,5, con una media de 75 y una desviación estándar de 10, tu puntuación real sería 75 + (1,5 × 10) = 90.

Cómo calcular una puntuación Z

La conversión de datos brutos a puntuaciones z implica un proceso sistemático que, con la práctica, se convierte en algo natural.

Cálculo paso a paso

A continuación se explica cómo calcular manualmente las puntuaciones z: En primer lugar, calcula la media de tu distribución sumando todos los valores y dividiéndolos por el recuento. A continuación, calcula la desviación estándar hallando la raíz cuadrada de la media de las diferencias al cuadrado con respecto a la media. Por último, aplica la fórmula de la puntuación z restando la media de tu puntuación bruta y dividiendo por la desviación estándar.

Veamos un ejemplo: Si las puntuaciones de los exámenes de 85, 92, 78, 96 y 88 representan nuestro conjunto de datos completo (media = 87,8, desviación estándar = 6,14), una puntuación de 92 tiene una puntuación z de (92 - 87,8) / 6,14 = 0,68.

También puedes calcular rápidamente las puntuaciones z utilizando la función « STANDARDIZE() » (Puntuación z) de Excel o la misma función de Google Sheets, combinada con AVERAGE() y STDEV.P() para los datos de población o STDEV.S() para los datos de la muestra.

Directrices de interpretación

La interpretación de la puntuación Z sigue reglas direccionales coherentes, independientemente de tus datos originales. Las puntuaciones z positivas indican valores por encima de la media, mientras que las puntuaciones z negativas muestran valores por debajo de la media. Una puntuación z de 0 significa que tu punto de datos es exactamente igual a la media.

Para datos distribuidos normalmente, puedes aplicar pautas interpretativas adicionales: los valores con puntuaciones z superiores a ±2 son inusuales (ocurren en aproximadamente el 5 % de los casos), mientras que las puntuaciones z superiores a ±3 son raras (probabilidad inferior al 1 %). Puedes encontrar los percentiles exactos para distribuciones normales utilizando tablas z, que muestran qué porcentaje de observaciones se encuentra por debajo de cualquier puntuación z dada.

En el caso de datos no normales, las puntuaciones z siguen indicando la posición relativa y ayudan a identificar posibles valores atípicos, pero los porcentajes específicos no son aplicables.

Interpretación de las puntuaciones Z y la desviación estándar

Comprender la relación entre las puntuaciones z y la desviación estándar te ayuda a entender lo que realmente representan estos valores estandarizados.

Relación con la desviación estándar

Las puntuaciones Z miden directamente la distancia respecto a la media en unidades de desviación estándar. Una puntuación z de 2,5 significa que tu punto de datos se sitúa 2,5 desviaciones estándar por encima de la media. Esto difiere de la desviación estándar en sí, que mide la dispersión típica de los datos alrededor de la media.

La desviación estándar describe la variabilidad dentro de un único conjunto de datos, mientras que las puntuaciones z permiten comparar diferentes conjuntos de datos con medias y dispersiones diferentes. Piensa en la desviación estándar como la medida de la «amplitud» de tu distribución, mientras que las puntuaciones z te indican exactamente dónde se sitúan los puntos individuales dentro de esa amplitud.

Porcentaje de observaciones por debajo de una puntuación z

Para datos distribuidos normalmente, las tablas z convierten las puntuaciones z en rangos percentiles, mostrando qué porcentaje de observaciones se encuentra por debajo de tu valor. En una distribución normal, una puntuación z de 1,0 corresponde al percentil 84, lo que significa que el 84 % de las observaciones son menores.

Las modernas calculadoras en línea y los programas estadísticos permiten realizar estas conversiones al instante para distribuciones normales. Sin embargo, para datos no normales, necesitarás métodos específicos de distribución para determinar los percentiles, ya que los porcentajes estándar de la tabla z no serán aplicables.

Aplicaciones de las puntuaciones Z

Las puntuaciones Z aparecen en todas las estadísticas y en la ciencia de datos, resolviendo problemas prácticos en diversos campos.

Estimación de probabilidades y comprobación de hipótesis

Las puntuaciones Z constituyen la base de los cálculos de probabilidad en las distribuciones normales. Cuando quieres hallar la probabilidad de obtener una puntuación superior a 600 en una prueba con distribución normal, con una media de 500 y una desviación estándar de 100, primero conviertes 600 en una puntuación z de 1,0 y, a continuación, buscas la probabilidad correspondiente (aproximadamente el 16 %). También puedes calcular las probabilidades entre dos puntuaciones z hallando la diferencia entre sus probabilidades acumulativas.

En la comprobación de hipótesis, las puntuaciones z ayudan a determinar la significación estadística comparando las estadísticas de la muestra con los valores esperados de la población bajoel supuesto de normalidad. Nuestro curso «Prueba de hipótesis en R» abarca estas aplicaciones y muestra cómo las puntuaciones z se relacionan con los valores p y los intervalos de confianza. 

Detección de valores atípicos y estandarización de datos

Los científicos de datos utilizan habitualmente las puntuaciones z para identificar posibles valores atípicos. En el caso de datos con distribución normal, los valores con puntuaciones z superiores a ±3 son muy poco habituales (se dan en menos del 1 % de los casos) y suelen indicar errores en la introducción de datos, problemas de medición o casos realmente excepcionales que merece la pena investigar. Incluso con datos no normales, las puntuaciones z extremas pueden señalar observaciones que merecen un examen más detallado.

La estandarización de conjuntos de datos completos con puntuaciones z crea variables con una media de 0 y una desviación estándar de 1, lo que las hace directamente comparables. Esto resulta muy útil en algoritmos de machine learning que son sensibles a las diferencias de escala, como el agrupamiento k-means o las redes neuronales. 

Comparación de puntuaciones en diferentes escalas

Las puntuaciones Z permiten realizar comparaciones justas entre diferentes pruebas o mediciones con formas de distribución similares. Esa comparación anterior entre el SAT y el ACT se vuelve sencilla una vez que conviertes ambas puntuaciones a puntuaciones z utilizando sus respectivas medias y desviaciones estándar. Un estudiante con una puntuación z de 1,2 en el SAT superó a alguien con una puntuación z de 0,8 en el ACT, independientemente de la diferencia de escala.

Aplicaciones avanzadas en estadística y ciencia de datos

Las puntuaciones Z aparecen en técnicas analíticas sofisticadas como el análisis de conglomerados (donde la estandarización garantiza que todas las variables contribuyan por igual), el escalado multidimensional y el análisis de componentes principales. 

En el análisis de regresión, los coeficientes estandarizados (también llamados coeficientes beta) te ayudan a comparar la importancia relativa de los predictores continuos al colocarlos en la misma escala. El proceso consiste en convertir todas las variables (tanto predictoras como de resultado) a puntuaciones z antes de ejecutar la regresión. Los coeficientes estandarizados resultantes indican «¿cuántas desviaciones estándar se espera que cambie el resultado cuando este predictor aumente en una desviación estándar?», lo que permite realizar comparaciones directas entre predictores con diferentes unidades originales.

Evaluación sanitaria y educativa

Los profesionales médicos utilizan las puntuaciones z para interpretar los resultados de las pruebas comparándolos con los datos de referencia de la población. Las puntuaciones Z de densidad ósea comparan las mediciones individuales con las de personas de la misma edad, lo que ayuda a diagnosticar afecciones como la osteoporosis. Las evaluaciones educativas se basan en puntuaciones z para estandarizar los resultados de las pruebas entre diferentes años y poblaciones, lo que permite realizar comparaciones justas a pesar de las diferentes condiciones de las pruebas. 

Métodos y herramientas computacionales

El análisis moderno se basa en herramientas de software que automatizan los cálculos de la puntuación z.

Tablas Z y conversión de percentiles

Las tablas Z tradicionales siguen siendo útiles para comprender la relación entre las puntuaciones Z y las probabilidades en las distribuciones normales. Estas tablas enumeran las probabilidades acumulativas para los valores de la distribución normal estándar, que suelen oscilar entre z = -3,49 y z = 3,49. Para leer una tabla z, busca los dos primeros dígitos de tu puntuación z en la columna izquierda y, a continuación, localiza el tercer dígito en la fila superior.

Uso de la programación para calcular puntuaciones z

Ya hemos hablado de la función « STANDARDIZE() » de Excel en la sección dedicada al cálculo paso a paso. Para Python y R, veamos el mismo ejemplo utilizando las calificaciones de los exámenes: 85, 92, 78, 96, 88.

Python con scipy.stats:

import numpy as np
from scipy import stats

# Our exam scores
scores = np.array([85, 92, 78, 96, 88])

# Calculate z-scores using scipy (uses population std by default)
# This means dividing by N, not N-1
z_scores = stats.zscore(scores)
print(f"Z-scores: {z_scores}")
# Output: [-0.46  0.68 -1.59  1.33  0.03]

# Manual calculation for verification
mean_score = np.mean(scores)
std_score = np.std(scores, ddof=0)  # Population standard deviation
z_manual = (scores - mean_score) / std_score
print(f"Manual z-scores: {z_manual}")

R utilizando la función scale():

# Our exam scores
scores <- c(85, 92, 78, 96, 88)

# Calculate z-scores using scale() (uses sample std by default)
z_scores <- scale(scores)[,1]  # Extract vector from matrix
print(paste("Z-scores:", z_scores))
# Output: [-0.41  0.61 -1.43  1.19  0.03]

# Manual calculation for verification
z_manual <- (scores - mean(scores)) / sd(scores)
print(paste("Manual z-scores:", z_manual))

Ten en cuenta que Python y R dan resultados ligeramente diferentes porque scipy.stats.zscore() utiliza la desviación estándar de la población (dividiendo por N), mientras que R's scale() utiliza la desviación estándar de la muestra (dividiendo por N-1). Para nuestra puntuación de 92, Python da una puntuación z de 0,68, mientras que R da 0,61. Ambas opciones son correctas, dependiendo de si tratas tus datos como una población completa o como una muestra. 

Conclusión

Las puntuaciones Z sirven de puente entre los datos brutos y una interpretación estadística significativa. Permiten realizar comparaciones justas entre diferentes escalas, facilitan los cálculos de probabilidad cuando los datos siguen distribuciones normales y ayudan a identificar observaciones inusuales que merecen ser investigadas.

Estos valores estandarizados abarcan desde el análisis básico de datos hasta aplicaciones avanzadas de machine learning, lo que los convierte en herramientas útiles para cualquiera que trabaje con datos cuantitativos. Explora nuestro curso Inferencia para datos numéricos en R para ver técnicas de inferencia estadística con conjuntos de datos reales, y nuestro curso Pruebas A/B en R para métodos de prueba de hipótesis en los que se aplican con frecuencia conceptos de puntuación z.