Z-Score: Der komplette Leitfaden zur statistischen Standardisierung

Du vergleichst die SAT-Ergebnisse von 2020 mit den ACT-Ergebnissen aus demselben Jahr. Ein Schüler hat beim SAT 1200 Punkte gemacht, während ein anderer beim ACT 24 Punkte erreicht hat, aber welche Leistung ist besser? Genau dieses Problem lösen Z-Scores, indem sie verschiedene Messungen auf eine gemeinsame Skala bringen.

Z-Scores machen aus Rohdaten standardisierte Werte, sodass man verschiedene Verteilungen sinnvoll miteinander vergleichen kann. Diese Standardisierung ist super, wenn du Daten aus verschiedenen Quellen analysierst, Ausreißer findest oder Wahrscheinlichkeiten in statistischen Analysen berechnest. Wir schauen uns die mathematischen Grundlagen von Z-Scores an, gehen Schritt für Schritt praktische Berechnungsmethoden durch und wenden diese Techniken auf verschiedene Szenarien an. 

Was ist ein Z-Score?

Z-Scores bieten dir eine standardisierte Methode, um zu verstehen, wo ein Datenpunkt im Verhältnis zu seiner Verteilung steht.

Definition und Kernformel

Ein Z-Score zeigt an, wie viele Standardabweichungen ein Datenpunkt vom Mittelwert seiner Verteilung entfernt ist. Die Formel ist einfach:

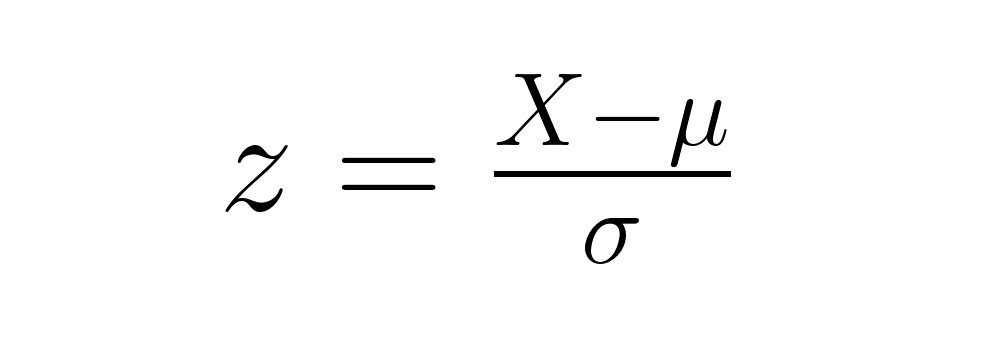
wobei X deine Rohpunktzahl ist, μ (mu) der Populationsmittelwert und σ (sigma) die Populationsstandardabweichung. Mit Z-Scores kannst du Datenpunkte aus verschiedenen Verteilungen direkt vergleichen, egal welche Einheiten oder Skalen sie ursprünglich hatten.

Eigenschaften der Standardnormalverteilung

Z-Scores wandeln normalverteilte Daten in die Standardnormalverteilung um, die eine spezielle Glockenkurve mit Mittelwert = 0 und Standardabweichung = 1 ist. Diese Umwandlung macht ein paar coole Analysefunktionen möglich: Ungefähr 68 % der Werte liegen innerhalb einer Standardabweichung vom Mittelwert (Z-Werte zwischen -1 und +1), 95 % liegen innerhalb von zwei Standardabweichungen (-2 bis +2) und 99,7 % liegen innerhalb von drei Standardabweichungen (-3 bis +3).

Z-Score-Formel und Varianten

Die grundlegende Z-Score-Formel funktioniert gut für Bevölkerungsdaten, aber in der Praxis muss man sie oft ein bisschen anpassen, je nachdem, um welche Art von Daten und welche Stichprobengröße es geht.

Standard-Z-Score-Formeln

Wie schon gesagt, die Grundformel für einen Z-Score ist: 

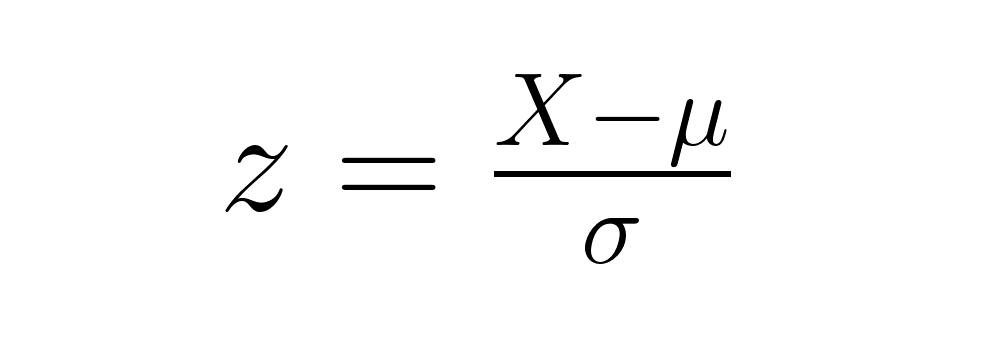
Von diesem Punkt aus gibt es Unterschiede, je nachdem, ob du mit Stichprobendaten arbeitest oder einen Stichprobenmittelwert gegen einen Populationsmittelwert testest. 

Für einzelne Datenpunkte in einer Stichprobe: 

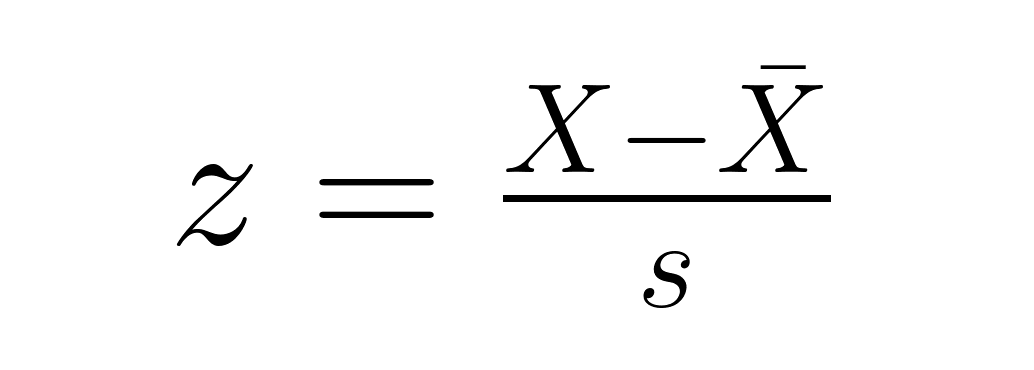
wobei X̄ der Stichprobenmittelwert und s die Stichprobenstandardabweichung ist (berechnet mit der De-Zähler n−1). Diese Version zeigt, wie weit ein Punkt in Standardabweichungen vom Mittelwert der Stichprobe entfernt ist. Das ist praktisch, um relative Positionen und mögliche Ausreißer in deinem Datensatz zu erkennen.

Wenn wir prüfen, ob sich der Mittelwert einer Stichprobe deutlich vom Mittelwert einer Grundgesamtheit unterscheidet, nehmen wir den Standardfehler des Mittelwerts in unsere Berechnung mit rein:

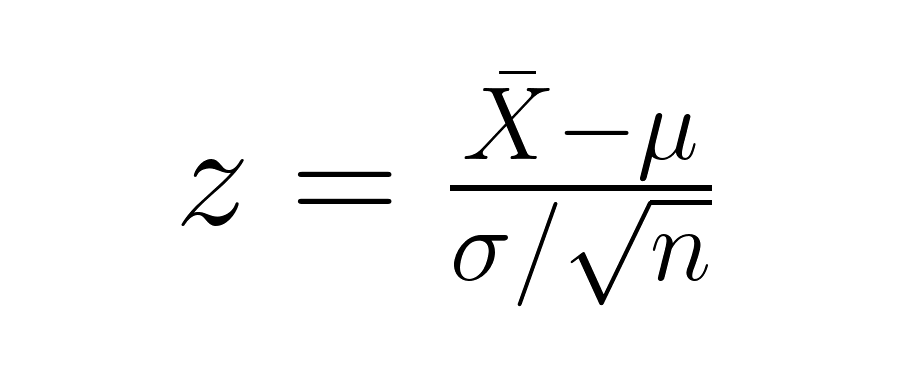
wobei X̄ dein Stichprobenmittelwert, μ der Populationsmittelwert, σ die Populationsstandardabweichung und n deine Stichprobengröße ist. Der Nenner (σ/√n) ist der Standardfehler des Mittelwerts, der die Stichprobengröße bei der Hypothesentestung berücksichtigt.

Berechnung einer Rohpunktzahl aus einem Z-Wert

Manchmal geht man von den Z-Werten rückwärts, um die ursprünglichen Werte zu finden. Wenn du die Formel umstellst, bekommst du: 

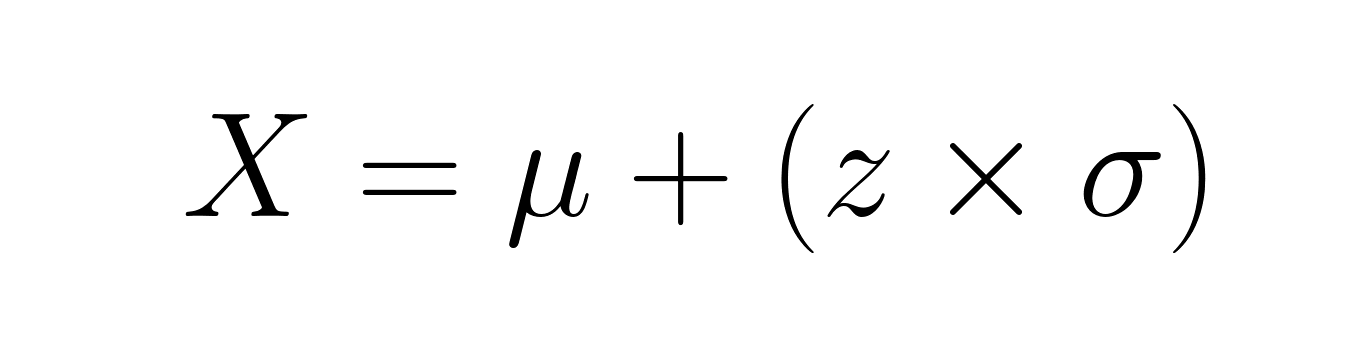
Wenn ein Schüler bei einer Prüfung mit einem Mittelwert von 75 und einer Standardabweichung von 10 einen Z-Wert von 1,5 hat, wäre seine tatsächliche Punktzahl 75 + (1,5 × 10) = 90.

Wie man einen Z-Score berechnet

Die Umwandlung von Rohdaten in Z-Werte ist ein systematischer Prozess, der mit der Zeit ganz einfach wird.

Schrittweise Berechnung

So berechnest du Z-Scores manuell: Zuerst musst du den Mittelwert deiner Verteilung berechnen, indem du alle Werte addierst und durch die Anzahl teilst. Berechne dann die Standardabweichung, indem du die Quadratwurzel aus den quadrierten Abweichungen vom Mittelwert nimmst. Zum Schluss nimmst du die Z-Score-Formel, indem du den Mittelwert von deiner Rohpunktzahl abziehst und durch die Standardabweichung teilst.

Schauen wir uns mal ein Beispiel an: Wenn die Prüfungsergebnisse 85, 92, 78, 96, 88 unseren kompletten Datensatz darstellen (Mittelwert = 87,8, Standardabweichung = 6,14), hat ein Ergebnis von 92 einen Z-Wert von (92 - 87,8) / 6,14 = 0,68.

Du kannst Z-Scores auch schnell mit der Excel-Funktion „ STANDARDIZE() “ oder der gleichen Funktion in Google Sheets berechnen, zusammen mit AVERAGE() und STDEV.P() für Bevölkerungsdaten oder STDEV.S() für Stichprobendaten.

Richtlinien zur Auslegung

Die Interpretation des Z-Werts folgt einheitlichen Richtungsregeln, egal wie deine ursprünglichen Daten aussehen. Positive Z-Werte zeigen Werte über dem Mittelwert an, während negative Z-Werte Werte unter dem Mittelwert anzeigen. Ein Z-Wert von 0 heißt, dass dein Datenpunkt genau dem Mittelwert entspricht.

Bei normalverteilten Daten kannst du noch ein paar zusätzliche Interpretationsregeln anwenden: Werte mit Z-Scores über ±2 sind ungewöhnlich (treten in etwa 5 % der Fälle auf), während Z-Scores über ±3 echt selten sind (Wahrscheinlichkeit unter 1 %). Du kannst die genauen Perzentile für Normalverteilungen mit Hilfe von Z-Tabellen ermitteln, die zeigen, wie viel Prozent der Beobachtungen unter einem bestimmten Z-Wert liegen.

Bei nicht normalen Daten zeigen Z-Scores immer noch die relative Position an und helfen dabei, mögliche Ausreißer zu erkennen, aber die genauen Prozentsätze sind nicht relevant.

Z-Werte und Standardabweichung verstehen

Wenn du die Beziehung zwischen Z-Scores und Standardabweichung verstehst, kannst du besser begreifen, was diese standardisierten Werte eigentlich bedeuten.

Verhältnis zur Standardabweichung

Z-Werte messen direkt den Abstand vom Mittelwert in Standardabweichungseinheiten. Ein Z-Wert von 2,5 heißt, dass dein Datenpunkt 2,5 Standardabweichungen über dem Mittelwert liegt. Das ist anders als bei der Standardabweichung, die die typische Streuung der Daten um den Mittelwert misst.

Die Standardabweichung zeigt, wie sehr sich die Werte in einem Datensatz voneinander unterscheiden, während man mit Z-Scores verschiedene Datensätze mit unterschiedlichen Mittelwerten und Streuungen vergleichen kann. Stell dir die Standardabweichung als Messung der „Breite“ deiner Verteilung vor, während Z-Werte dir genau sagen, wo einzelne Punkte innerhalb dieser Breite liegen.

Prozentualer Anteil der Beobachtungen unter einem Z-Wert

Bei normalverteilten Daten wandeln Z-Tabellen Z-Werte in Perzentilränge um und zeigen, wie viel Prozent der Beobachtungen unter deinem Wert liegen. Bei einer Normalverteilung ist ein Z-Wert von 1,0 wie das 84. Perzentil, was heißt, dass 84 % der Werte kleiner sind.

Mit modernen Online-Rechnern und Statistik-Software kann man diese Umrechnungen für Normalverteilungen sofort machen. Bei nicht normalen Daten brauchst du allerdings verteilungsspezifische Methoden, um Perzentile zu bestimmen, weil die Standard-Z-Tabellen-Prozentsätze hier nicht funktionieren.

Anwendungen von Z-Scores

Z-Scores tauchen überall in der Statistik und Datenwissenschaft auf und helfen dabei, praktische Probleme in verschiedenen Bereichen zu lösen.

Wahrscheinlichkeitsschätzung und Hypothesentests

Z-Werte sind die Basis für Wahrscheinlichkeitsberechnungen bei Normalverteilungen. Wenn du die Wahrscheinlichkeit herausfinden willst, mit der man bei normalverteilten Prüfungsergebnissen mit einem Mittelwert von 500 und einer Standardabweichung von 100 mehr als 600 Punkte erreicht, rechnest du zuerst 600 in einen Z-Wert von 1,0 um und schaust dann die entsprechende Wahrscheinlichkeit nach (etwa 16 %). Du kannst auch die Wahrscheinlichkeiten zwischen zwei Z-Werten berechnen, indem du die Differenz zwischen ihren kumulativen Wahrscheinlichkeiten ermittelst.

Bei der Hypothesentestung helfen Z-Scores dabei, die statistische Signifikanz zu bestimmen, indem sie die Stichprobenstatistik mit den erwarteten Populationswerten vergleichen, wobeiman davon ausgeht, dass die Daten normalverteilt sind. Unser Kurs „Hypothesentests in R” geht auf diese Anwendungen ein und zeigt, wie Z-Werte mit p-Werten und Konfidenzintervallen zusammenhängen. 

Ausreißererkennung und Datenstandardisierung

Datenwissenschaftler nutzen regelmäßig Z-Scores, um mögliche Ausreißer zu erkennen. Bei normalverteilten Daten sind Werte mit Z-Scores über ±3 echt ungewöhnlich (sie kommen in weniger als 1 % der Fälle vor) und deuten oft auf Fehler bei der Dateneingabe, Messprobleme oder wirklich außergewöhnliche Fälle hin, die man genauer anschauen sollte. Selbst bei nicht normalen Daten können extreme Z-Werte auf Beobachtungen hinweisen, die genauer angeschaut werden sollten.

Wenn man ganze Datensätze mit Z-Scores standardisiert, bekommt man Variablen mit einem Mittelwert von 0 und einer Standardabweichung von 1, sodass sie direkt miteinander verglichen werden können. Das ist echt nützlich bei Algorithmen für maschinelles Lernen, die empfindlich auf Größenunterschiede reagieren, wie zum Beispiel k-Means-Clustering oder neuronale Netze. 

Vergleich von Punktzahlen auf verschiedenen Skalen

Z-Scores machen es möglich, verschiedene Tests oder Messungen mit ähnlichen Verteilungsformen fair zu vergleichen. Der frühere Vergleich zwischen SAT und ACT wird einfach, wenn man beide Ergebnisse anhand ihrer jeweiligen Mittelwerte und Standardabweichungen in Z-Werte umrechnet. Ein Schüler mit einem SAT-Z-Wert von 1,2 hat besser abgeschnitten als jemand mit einem ACT-Z-Wert von 0,8, auch wenn die Skalen unterschiedlich sind.

Fortgeschrittene Anwendungen in Statistik und Datenwissenschaft

Z-Scores kommen in komplexen Analysetechniken wie der Clusteranalyse (wo die Standardisierung dafür sorgt, dass alle Variablen gleich viel beitragen), der multidimensionalen Skalierung und der Hauptkomponentenanalyse vor. 

In der Regressionsanalyse helfen standardisierte Koeffizienten (auch Beta-Koeffizienten genannt) dabei, die relative Bedeutung von kontinuierlichen Prädiktoren zu vergleichen, indem sie auf derselben Skala dargestellt werden. Der Prozess beinhaltet, dass alle Variablen (sowohl Prädiktoren als auch Ergebnisse) in Z-Scores umgewandelt werden, bevor die Regression durchgeführt wird. Die standardisierten Koeffizienten zeigen dir, um wie viele Standardabweichungen sich das Ergebnis voraussichtlich ändert, wenn dieser Prädiktor um eine Standardabweichung steigt. So kannst du verschiedene Prädiktoren mit unterschiedlichen ursprünglichen Einheiten direkt miteinander vergleichen.

Gesundheitswesen und Bildungsbewertung

Mediziner nutzen Z-Scores, um Testergebnisse zu interpretieren, indem sie sie mit Referenzdaten der Bevölkerung vergleichen. Die Z-Scores der Knochendichte vergleichen einzelne Messungen mit denen von Gleichaltrigen und helfen dabei, Krankheiten wie Osteoporose zu erkennen. Bildungsbewertungen nutzen Z-Scores, um Testergebnisse über verschiedene Jahre und Bevölkerungsgruppen hinweg zu standardisieren, sodass trotz unterschiedlicher Testbedingungen faire Vergleiche möglich sind. 

Rechenmethoden und Werkzeuge

Moderne Analysen nutzen Software-Tools, die die Berechnung von Z-Scores automatisch machen.

Z-Tabellen und Prozentrangumrechnung

Traditionelle Z-Tabellen sind immer noch super, um den Zusammenhang zwischen Z-Werten und Wahrscheinlichkeiten in Normalverteilungen zu verstehen. Diese Tabellen zeigen die kumulativen Wahrscheinlichkeiten für Werte der Standardnormalverteilung, die normalerweise von z = -3,49 bis z = 3,49 reichen. Um eine Z-Tabelle zu lesen, suchst du die ersten beiden Ziffern deines Z-Werts in der linken Spalte und dann die dritte Ziffer in der obersten Zeile.

Z-Scores mit Programmierung berechnen

Wir haben die Excel-Funktion „ STANDARDIZE() “ schon im Abschnitt „Schrittweise Berechnung“ behandelt. Für Python und R schauen wir uns mal dasselbe Beispiel mit Prüfungsergebnissen an: 85, 92, 78, 96, 88.

Python mit scipy.stats:

import numpy as np
from scipy import stats

# Our exam scores
scores = np.array([85, 92, 78, 96, 88])

# Calculate z-scores using scipy (uses population std by default)
# This means dividing by N, not N-1
z_scores = stats.zscore(scores)
print(f"Z-scores: {z_scores}")
# Output: [-0.46  0.68 -1.59  1.33  0.03]

# Manual calculation for verification
mean_score = np.mean(scores)
std_score = np.std(scores, ddof=0)  # Population standard deviation
z_manual = (scores - mean_score) / std_score
print(f"Manual z-scores: {z_manual}")

R mit der Funktion scale():

# Our exam scores
scores <- c(85, 92, 78, 96, 88)

# Calculate z-scores using scale() (uses sample std by default)
z_scores <- scale(scores)[,1]  # Extract vector from matrix
print(paste("Z-scores:", z_scores))
# Output: [-0.41  0.61 -1.43  1.19  0.03]

# Manual calculation for verification
z_manual <- (scores - mean(scores)) / sd(scores)
print(paste("Manual z-scores:", z_manual))

Beachte, dass Python und R leicht unterschiedliche Ergebnisse liefern, weil Python ( scipy.stats.zscore() ) die Standardabweichung der Grundgesamtheit (geteilt durch N) verwendet, während R ( scale() ) die Standardabweichung der Stichprobe (geteilt durch N-1) nimmt. Für unsere Punktzahl von 92 gibt Python einen Z-Score von 0,68, während R einen Wert von 0,61 liefert. Beide sind richtig, je nachdem, ob du deine Daten als komplette Population oder als Stichprobe behandelst. 

Fazit

Z-Scores sind wie eine Brücke zwischen den Rohdaten und einer sinnvollen statistischen Interpretation. Sie machen faire Vergleiche über verschiedene Skalen hinweg möglich, helfen bei Wahrscheinlichkeitsberechnungen, wenn die Daten normal verteilt sind, und unterstützen dabei, ungewöhnliche Beobachtungen zu erkennen, die genauer untersucht werden sollten.

Diese Standardwerte reichen von der einfachen Datenanalyse bis hin zu fortgeschrittenen Anwendungen des maschinellen Lernens und sind damit nützliche Werkzeuge für alle, die mit quantitativen Daten arbeiten. Schau dir unseren Kurs „Inferenz für numerische Daten in R” an, um statistische Inferenztechniken mit echten Datensätzen zu lernen, und unseren Kurs „A/B-Tests in R” für Hypothesentestmethoden, bei denen Z-Score-Konzepte oft zum Einsatz kommen.