Z-Score: The Complete Guide to Statistical Standardization

You’re comparing SAT scores from 2020 with ACT scores from the same year. One student scored 1200 on the SAT while another scored 24 on the ACT, but which performance is better? This is exactly the problem z-scores solve by converting different measurements to a common scale.

Z-scores transform raw data into standardized values, making meaningful comparisons possible across completely different distributions. This standardization helps when you're analyzing data from different sources, identifying outliers, or calculating probabilities in statistical analysis. We'll cover the mathematical foundations behind z-scores, work through practical calculation methods step by step, and apply these techniques to different scenarios. 

What Is a Z-Score?

Z-scores give you a standardized way to understand where any data point sits relative to its distribution.

Definition and core formula

A z-score represents the number of standard deviations a data point falls from its distribution's mean. The formula is simple:

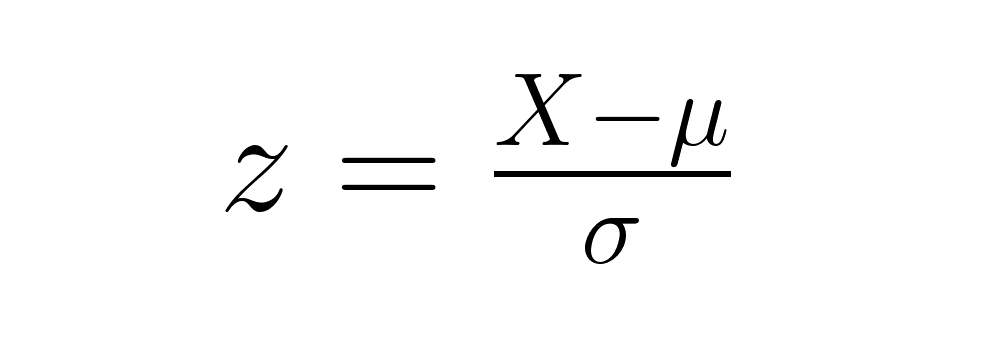
where X is your raw score, μ (mu) is the population mean, and σ (sigma) is the population standard deviation. Z-scores let you compare data points from different distributions directly, regardless of their original units or scales.

Properties of the standard normal distribution

Z-scores transform normally distributed data into the standard normal distribution which is a special bell curve with mean = 0 and standard deviation = 1. This transformation unlocks some useful analytical capabilities: approximately 68% of values fall within one standard deviation of the mean (Z-scores between -1 and +1), 95% fall within two standard deviations (-2 to +2), and 99.7% fall within three standard deviations (-3 to +3).

Z-Score Formula and Variations

The basic z-score formula works well for population data, but real-world analysis often requires slight modifications depending on your data type and sample size.

Standard z-score formulas

As introduced earlier, the basic formula for a z-score is: 

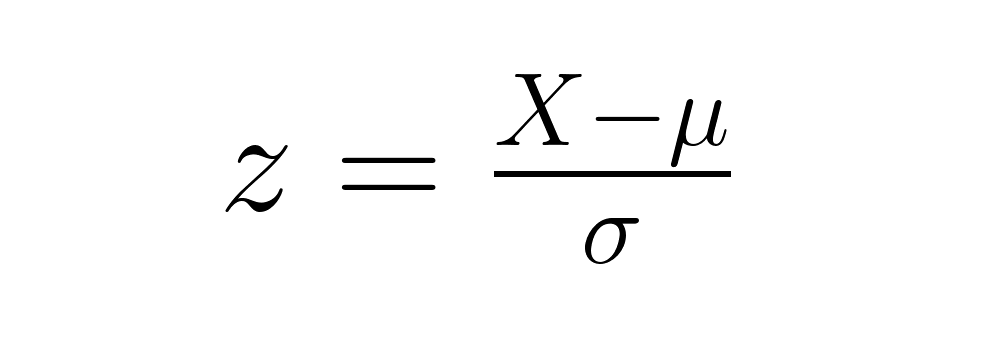
From this starting point, variations arise depending on whether you are working with sample data or testing a sample mean against a population mean. 

For individual data points in a sample: 

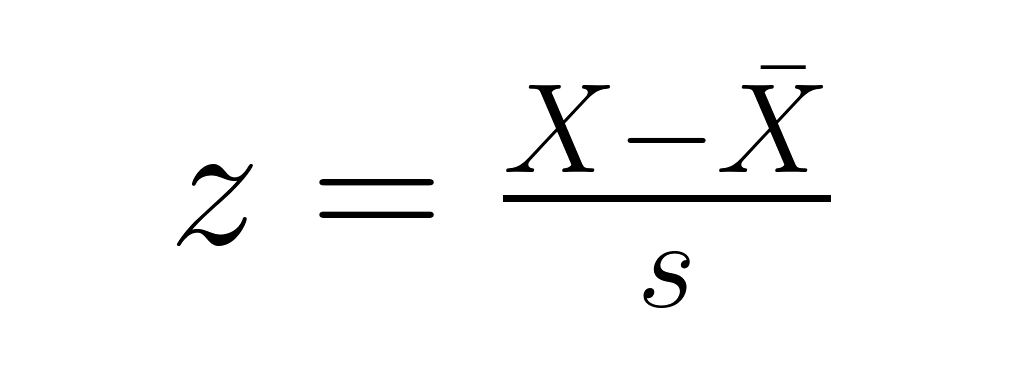
where X̄ is the sample mean and s is the sample standard deviation (calculated with denominator n−1). This version shows how many sample standard deviations a point is from the sample mean, which is useful for identifying relative positions and potential outliers within your dataset.

When testing whether a sample mean differs significantly from a population mean, we use the standard error of the mean in our calculation:

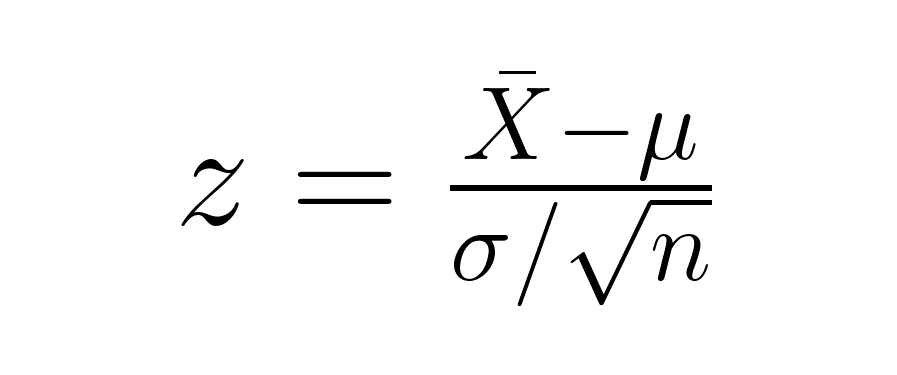
where X̄ is your sample mean, μ is the population mean, σ is the population standard deviation, and n is your sample size. The denominator (σ/√n) represents the standard error of the mean, which accounts for sample size in hypothesis testing.

Calculating a raw score from a z-score

Sometimes you work backwards from z-scores to find original values. Rearranging the formula gives you: 

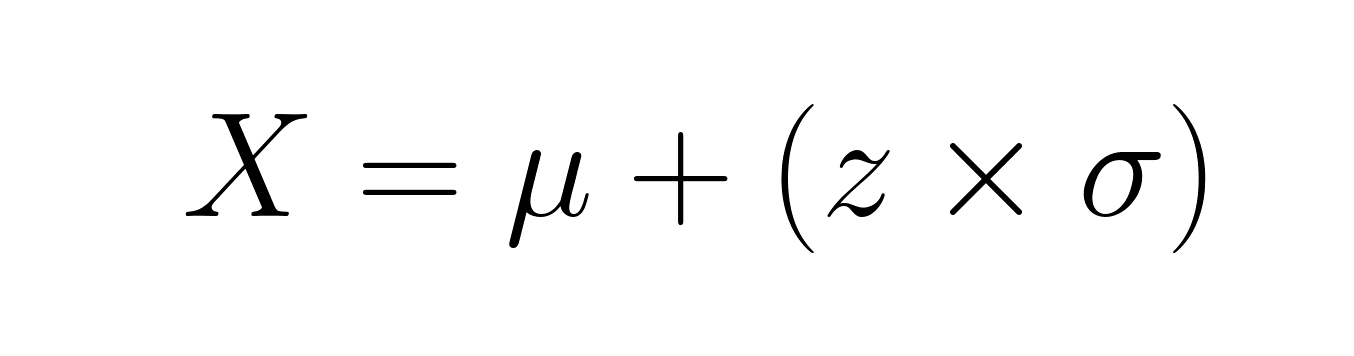
If a student's test score has a z-score of 1.5 on an exam with mean 75 and standard deviation 10, their actual score would be 75 + (1.5 × 10) = 90.

How to Calculate a Z-Score

Converting raw data to z-scores involves a systematic process that becomes second nature with practice.

Step-by-step computation

Here's how to calculate z-scores manually: First, find your distribution's mean by summing all values and dividing by the count. Next, calculate the standard deviation by finding the square root of the average squared differences from the mean. Finally, apply the z-score formula by subtracting the mean from your raw score and dividing by the standard deviation.

Let's work through an example: If exam scores of 85, 92, 78, 96, 88 represent our complete dataset (mean = 87.8, standard deviation = 6.14), a score of 92 has a z-score of (92 - 87.8) / 6.14 = 0.68.

You can also calculate z-scores quickly using Excel's STANDARDIZE() function or the same function in Google Sheets, combined with AVERAGE() and STDEV.P() for population data or STDEV.S() for sample data.

Interpretation guidelines

Z-score interpretation follows consistent directional rules regardless of your original data. Positive z-scores indicate values above the mean, while negative z-scores show values below the mean. A z-score of 0 means your data point equals the mean exactly.

For normally distributed data, you can apply additional interpretive guidelines: values with z-scores beyond ±2 are unusual (occurring in roughly 5% of cases), while z-scores beyond ±3 are rare (less than 1% probability). You can find exact percentiles for normal distributions using z-tables, which show what percentage of observations fall below any given z-score.

For non-normal data, z-scores still indicate relative position and help identify potential outliers, but the specific percentages don't apply.

Interpreting Z-Scores and Standard Deviation

Understanding the relationship between z-scores and standard deviation helps you grasp what these standardized values actually represent.

Relationship to standard deviation

Z-scores directly measure distance from the mean in standard deviation units. A z-score of 2.5 means your data point sits 2.5 standard deviations above the mean. This differs from standard deviation itself, which measures the typical spread of data around the mean.

Standard deviation describes variability within a single dataset, while z-scores allow comparison across different datasets with different means and spreads. Think of standard deviation as measuring the "width" of your distribution, while z-scores tell you exactly where individual points fall within that width.

Percentage of observations below a z-score

For normally distributed data, z-tables convert z-scores into percentile ranks, showing what percentage of observations fall below your value. In a normal distribution, a z-score of 1.0 corresponds to the 84th percentile, meaning 84% of observations are smaller.

Modern online calculators and statistical software make these conversions instant for normal distributions. However, for non-normal data, you'll need distribution-specific methods to determine percentiles, as the standard z-table percentages won't apply.

Applications of Z-Scores

Z-scores appear throughout statistics and data science, solving practical problems across diverse fields.

Probability estimation and hypothesis testing

Z-scores form the foundation of probability calculations in normal distributions. When you want to find the probability of scoring above 600 on normally distributed exam scores with mean 500 and standard deviation 100, you first convert 600 to a z-score of 1.0, then look up the corresponding probability (about 16%). You can also calculate probabilities between two z-scores by finding the difference between their cumulative probabilities.

In hypothesis testing, z-scores help determine statistical significance by comparing sample statistics to expected population values under the assumption of normality. Our Hypothesis Testing in R course covers these applications, showing how z-scores connect to p-values and confidence intervals. 

Outlier detection and data standardization

Data scientists regularly use z-scores to identify potential outliers. For normally distributed data, values with z-scores beyond ±3 are highly unusual (occurring less than 1% of the time) and often indicate data entry errors, measurement problems, or genuinely exceptional cases worth investigating. Even with non-normal data, extreme z-scores can flag observations that merit closer examination.

Standardizing entire datasets with z-scores creates variables with mean 0 and standard deviation 1, making them directly comparable. This proves valuable in machine learning algorithms that are sensitive to scale differences, such as k-means clustering or neural networks. 

Comparing scores on different scales

Z-scores enable fair comparisons across different tests or measurements with similar distribution shapes. That earlier SAT versus ACT comparison becomes straightforward once you convert both scores to z-scores using their respective means and standard deviations. A student with SAT z-score of 1.2 outperformed someone with ACT z-score of 0.8, regardless of the different scaling.

Advanced applications in statistics and data science

Z-scores appear in sophisticated analytical techniques like cluster analysis (where standardization ensures all variables contribute equally), multidimensional scaling, and principal components analysis. 

In regression analysis, standardized coefficients (also called beta coefficients) help you compare the relative importance of continuous predictors by putting them on the same scale. The process involves converting all variables (both predictors and outcomes) to z-scores before running the regression. The resulting standardized coefficients tell you "how many standard deviations the outcome is expected to change when this predictor increases by one standard deviation?" making direct comparisons possible across predictors with different original units.

Healthcare and educational assessment

Medical professionals use z-scores to interpret test results by comparing them to reference population data. Bone density z-scores compare individual measurements to age-matched peers, helping diagnose conditions like osteoporosis. Educational assessments rely on z-scores to standardize test results across different years and populations, enabling fair comparisons despite varying test conditions. 

Computational Methods and Tools

Modern analysis relies on software tools that automate z-score calculations.

Z-tables and percentile conversion

Traditional z-tables remain useful for understanding the connection between z-scores and probabilities in normal distributions. These tables list cumulative probabilities for standard normal distribution values, typically ranging from z = -3.49 to z = 3.49. To read a z-table, find your z-score's first two digits in the left column, then locate the third digit across the top row.

Using programming to calculate z-scores

We covered Excel's STANDARDIZE() function earlier in the step-by-step computation section. For Python and R, let's work through the same example using exam scores: 85, 92, 78, 96, 88.

Python with scipy.stats:

import numpy as np
from scipy import stats

# Our exam scores
scores = np.array([85, 92, 78, 96, 88])

# Calculate z-scores using scipy (uses population std by default)
# This means dividing by N, not N-1
z_scores = stats.zscore(scores)
print(f"Z-scores: {z_scores}")
# Output: [-0.46  0.68 -1.59  1.33  0.03]

# Manual calculation for verification
mean_score = np.mean(scores)
std_score = np.std(scores, ddof=0)  # Population standard deviation
z_manual = (scores - mean_score) / std_score
print(f"Manual z-scores: {z_manual}")

R using the scale() function:

# Our exam scores
scores <- c(85, 92, 78, 96, 88)

# Calculate z-scores using scale() (uses sample std by default)
z_scores <- scale(scores)[,1]  # Extract vector from matrix
print(paste("Z-scores:", z_scores))
# Output: [-0.41  0.61 -1.43  1.19  0.03]

# Manual calculation for verification
z_manual <- (scores - mean(scores)) / sd(scores)
print(paste("Manual z-scores:", z_manual))

Note that Python and R give slightly different results because scipy.stats.zscore() uses population standard deviation (dividing by N) while R's scale() uses sample standard deviation (dividing by N-1). For our score of 92, Python gives a z-score of 0.68 while R gives 0.61. Both are correct depending on whether you're treating your data as a complete population or a sample. 

Conclusion

Z-scores provide a bridge between raw data and meaningful statistical interpretation. They enable fair comparisons across different scales, support probability calculations when data follows normal distributions, and help identify unusual observations that merit investigation.

These standardized values extend from basic data analysis to advanced machine learning applications, making them useful tools for anyone working with quantitative data. Explore our Inference for Numerical Data in R course to see statistical inference techniques with real datasets, and our A/B Testing in R course for hypothesis testing methods where z-score concepts frequently apply.