Cours
Vous pouvez remarquer la courbe en cloche, qui porte plusieurs noms, comme la distribution normale ou la distribution gaussienne, pratiquement partout, surtout si vous avez un intérêt pour les statistiques ou la science des données. Cela ressemble à un accident de la nature, mais ce n'en est pas un : Il s'avère qu'une grande partie de ce que nous mesurons est le résultat de nombreux petits facteurs additionnés, ce qui indique la présence d'un modèle additif sous-jacent. Le théorème de la limite centrale explique pourquoi : Lorsqu'une variable est influencée par de nombreux petits facteurs indépendants, la somme de ces variables tend à suivre une distribution normale, indépendamment des distributions d'origine dont elles sont issues.
En transformant toute distribution normale en une forme spéciale appelée distribution normale standard, nous pouvons profiter de la présence de ce modèle additif et aller plus loin en normalisant cette distribution pour la rendre encore plus utile dans des contextes spécifiques. Nous étudierons comment la distribution normale standard est utilisée pour calculer des probabilités, faire des déductions statistiques et appliquer des tests statistiques en utilisant des propriétés bien établies de la distribution. À la fin de cet article, vous saurez clairement ce qu'est la distribution normale standard, pourquoi nous franchissons l'étape supplémentaire de la normaliser et comment tout cela est lié à la variabilité, aux probabilités et aux tests d'hypothèse. À la fin, j'espère que vous vous inscrirez également à notre cours Introduction aux statistiques en R ou à notre piste de compétences Inférence statistique en R pour continuer à développer les idées de cet article.
Qu'est-ce que la distribution normale standard ?
La distribution normale standard est une forme spécifique de la distribution normale où la moyenne est égale à zéro et l'écart type à un. Nous devrions également dire que la distribution est symétrique et que les probabilités de certaines valeurs diminuent symétriquement à mesure que l'on s'éloigne du centre.

"Distribution normale standard" Image par Dall-E
Comprendre les équations de la distribution normale standard
Examinons de plus près les aspects mathématiques de la distribution normale standard.
La PDF de la distribution normale standard
Si vous n'êtes pas familier avec l'idée d'une fonction de densité de probabilité (PDF), sachez qu'elle décrit la façon dont les probabilités sont distribuées sur les valeurs possibles d'une variable aléatoire continue. Chaque distribution de probabilité continue, comme la distribution exponentielle, la distribution t ou la distribution de Cauchy, possède sa propre fonction de densité de probabilité qui définit la courbe. La PDF de la distribution normale standard est définie ici :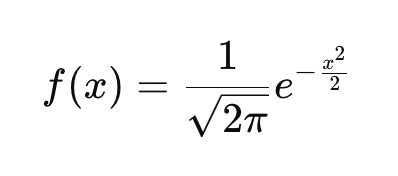
Cette fonction garantit que l'aire sous la courbe s'intègre à 1. Si vous examinez l'équation et introduisez différentes valeurs de x, vous obtenez la hauteur de la courbe en ces points. Dans l'équation :
- x représente un nombre réel quelconque et constitue la variable d'entrée de la fonction. Il apparaît dans l'exposant de la fonction, qui est -x2/2. Cela permet de contrôler la forme de la courbe.
- Comme x2 est toujours non négatif et qu'il y a un signe négatif devant, l'exposant est toujours négatif ou nul.
- Dans le cas spécifique où x=0, l'exposant est le plus grand, ce qui fait que f(x) atteint son maximum.
- Si x s'éloigne de 0 dans le sens positif ou négatif, x2 augmente, ce qui rend l'exposant plus négatif. Unexposant plus négatif se traduit par unevaleur de fonction plus petite, ce qui signifie, avec les autres choses que nous avons dites, que f(x) diminue symétriquement de part et d'autre de x=0.
- La base de l'exposant, qui est le nombre d'Euler, assure la décroissance rapide de la fonction à mesure que x s'éloigne de zéro dans l'une ou l'autre direction.
- La constante 1/√(2π) garantit que l'aire totale sous la courbe est égale à 1.
La fonction de distribution cumulative de la distribution normale standard
Contrairement à la FDP, qui donne la probabilité relative de différentes valeurs, la FCD vous indique la probabilité qu'une variable soit inférieure ou égale à une valeur donnée. Tout comme la PDF, chaque distribution de probabilité continue possède sa propre CDF.
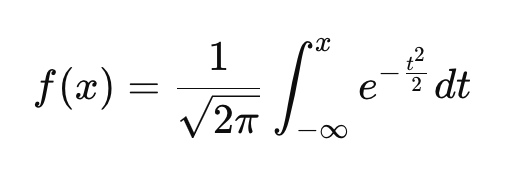
Cette équation est un peu plus compliquée, mais nous pouvons la résoudre :
- L'intégrale signifie qu'au lieu de donner la hauteur de la courbe à x, la FCD nous indique la probabilité totale de -∞ à x.
- Lorsque x→-∞, la CDF se rapproche de 0.
- Lorsque x=0 la FCD est de 0,5puisque la distribution est symétrique et que la moitié de la probabilité se situe à gauche de zéro.
- En tant que x→∞la FCD se rapproche de 1.
Pourquoi la distribution normale standard nous intéresse-t-elle ?
Notre guide sur la distribution gaussienne contient de bonnes idées sur les cas où vous souhaiteriez conformer vos données à une distribution normale. Mais il peut arriver que vous souhaitiez transformer vos données en une norme normale spécifique. Voici quelques raisons courantes :
La normale standard est utilisée dans les tests d'hypothèse
Une distribution normale standard rend nos données plus comparables et utilisables avec certaines méthodes statistiques. En convertissant les données en scores Z, nous pouvons comparer les observations entre différentes distributions normales. En particulier, elle constitue la base des tests Z, que nous utilisons lorsque nous voulons déterminer si la moyenne d'un échantillon diffère significativement de la moyenne d'une population.
Le test t, quant à lui, utilise l'écart-type de l'échantillon comme estimation de l'écart-type de la population, ce qui explique qu'il s'appuie sur la distribution t, dont les queues sont plus lourdes que celles de la distribution normale standard. Lisez notre tutoriel T-test vs. Test Z : Quand utiliser chaque, qui traite de sujets tels que la variance de la population et de l'échantillon.
La normale standard compare les données sur une échelle commune.
Comme les différents ensembles de données et variables peuvent avoir des unités et des échelles différentes, les comparaisons directes peuvent être difficiles. Mais lorsque vous les convertissez en scores Z en soustrayant la moyenne et en divisant par l'écart type, vous obtenez une comparaison facile entre différentes distributions. Lorsqu'on l'applique à un ensemble de données normalement distribuées, on obtient une distribution normale standard . Par exemple, la conversion des résultats du SAT et du GRE, dont je m'attends à ce qu'ils soient normalement distribués, en scores Z nous permet de comparer les performances des étudiants par rapport à leurs populations respectives.
La norme standard est utilisée dans le cadre du contrôle de la qualité
Cette norme est connue pour son importance dans le contrôle de la qualité des produits dans le secteur de la fabrication. En examinant de près les probabilités, les fabricants peuvent déterminer si les fluctuations de la qualité sont dues à des variations aléatoires ou à un autre problème sous-jacent. Ceci est lié aux tests d'hypothèses, que nous avons mentionnés précédemment, ainsi qu'à un tableau de score Z, dont nous parlerons plus loin.
La normale standard est utilisée dans la modélisation statistique
La distribution normale standard joue un rôle dans l'évaluation des erreurs dans des modèles tels que la régression linéaire et la prévision de séries chronologiques. Dans ces modèles, nous supposons que les résidus, qui sont les différences entre les valeurs observées et prédites, suivent non seulement une distribution normale, mais peuvent également être normalisés pour suivre une distribution normale standard.
En régression linéaire, les résidus normalisés sont des résidus qui ont été convertis en valeurs normalisées, ce qui nous permet de mesurer l'ampleur d'une erreur en unités d'écart-type, ce qui peut faciliter la détection des valeurs aberrantes. Ceci est utile car l' hétéroscédasticité des résidus, qui peut ne pas être évidente dans les prédicteurs du modèle, peut fausser l'interprétation des résidus.
Dans l'analyse des séries chronologiques, les erreurs de prévision sont souvent supposées suivre une distribution normale standard lorsqu'elles sont correctement normalisées. Ceci est important pour construire des intervalles de prédiction. De nombreux modèles de séries temporelles, tels que ARIMA, s'appuient sur les quantiles normaux standard pour définir les limites de confiance autour des prévisions. Également, dans la décomposition des séries temporelles, la composante restante, qui saisit les fluctuations irrégulières, est souvent normalement distribuée. Si vous normalisez cette composante résiduelle, vous pouvez trouver la probabilité de valeurs extrêmes dans votre série temporelle dont vous savez qu'elles ne sont pas le résultat de la tendance-cycle ou de la saisonnalité. Notre cours Forecasting in R vous apprendra ce type de techniques.
La normale standard est utilisée dans l'apprentissage automatique
De nombreux algorithmes d'apprentissage automatique fonctionnent mieux lorsque les données sont à l'échelle standard. Je pense à la régression logistique, au regroupement k-means et aux réseaux neuronaux .
Je pense également à l' analyse en composantes principales, qui est souvent utilisée comme technique de prétraitement. Dans l'ACP, nous voulons que nos caractéristiques d'entrée aient une moyenne nulle et une variance unitaire afin d'aider à empêcher les caractéristiques ayant de grandes valeurs de dominer. Une étape de prétraitement courante consiste à normaliser les données en soustrayant la moyenne et en la divisant par l'écart-type. Cela garantit que chaque caractéristique a une moyenne nulle et une variance unitaire, mais il convient de préciser que cela n'impose pas la normalité. Toutefois, dans certains cas, je m'attends à ce que les données transformées se rapprochent de la normalité si la distribution d'origine était déjà proche de la normale.
La normale standard est utilisée pour les calculs de probabilité
La fonction de distribution cumulative de la loi normale standard, dont nous avons parlé précédemment, est bien tabulée, c'est-à-dire précalculée et organisée en tableaux largement disponibles, ce qui facilite les calculs de probabilité puisqu'il suffit d'utiliser le tableau pour trouver la valeur correcte.
Par exemple, pour trouver la probabilité qu'une taille choisie au hasard soit inférieure à 1,80 m, nous normalisons la taille en utilisant la distribution normale de la population et nous recherchons le score Z dans un tableau normal standard. J'ai placé une version du tableau normal standard au bas de cet article au cas où vous auriez besoin de l'utiliser.
Transformations pour aligner les données sur la distribution normale standard
Les transformations peuvent aider à remodeler les données en une distribution normale standard. En gros, il s'agirait d'un processus en deux parties. Tout d'abord, nous remodelons nos données pour qu'elles deviennent normales, puis nous procédons à la normalisation du score Z.
Notez que vous n'appliquerez généralement pas la normalisation du score Z dans un premier temps, car les valeurs extrêmes peuvent fausser l'écart-type, la moyenne et l'écart-type étant sensibles aux valeurs aberrantes. De plus, certaines transformations nécessitent des données positives. Si vous appliquez d'abord la normalisation du score Z, les valeurs centrées sur la moyenne peuvent inclure des nombres négatifs, ce qui peut poser des problèmes pour les transformations qui ne fonctionnent qu'avec des valeurs positives. Je pense en particulier aux logarithmes. Il est donc préférable de procéder dans l'ordre : étape 1, puis étape 2.
Étape 1 : Transformer les données pour les rendre normales
Voici quelques idées de transformation que vous pourriez utiliser :
Transformation logarithmique pour les données asymétriques
Lorsque les données sont positivement asymétriques, une transformation logarithmique peut aider à les normaliser. Par exemple, l'application du logarithme aux valeurs brutes comprime les grandes valeurs, réduisant ainsi l'asymétrie et créant une distribution plus symétrique.
Transformation de la racine carrée pour les données de comptage
Pour les données de comptage ou les ensembles de données modérément asymétriques, nous pouvons essayer une transformation en racine carrée. Cette méthode réduit la variabilité tout en conservant une structure plus symétrique, ce qui rapproche les données de la forme de la courbe en cloche.
Transformation de Box-Cox pour des ajustements flexibles
La transformation de Box-Cox va plus loin en adaptant la transformation aux données. Son paramètre λ détermine la formule exacte appliquée, ce qui la rend très polyvalente pour aligner les données sur les propriétés de la distribution normale standard. Feature Engineering in R vous montrera la méthode Box-Cox, parmi de nombreuses autres méthodes importantes et utiles.
Étape 2 : Effectuer la normalisation des scores Z
Une fois qu'une transformation a été appliquée, les données peuvent être normalisées pour correspondre à la distribution normale standard. Cela permet d'ajuster les données pour qu'elles aient une moyenne de zéro et un écart-type de un. La formule du score Z est la suivante :
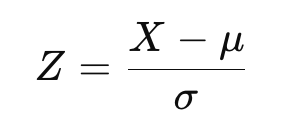
où X est la donnée transformée, μ est la moyenne, et σ est l'écart-type.
Si vous connaissez la distinction entre le score Z d'une population et le score Z d'un échantillon, comme nous l'expliquons dans notre cursus Inférence statistique en R, vous reconnaîtrez peut-être l'équation ci-dessus comme l'équation du score Z d'une population. Si vous travaillez avec un échantillon plutôt qu'avec l'ensemble de la population, nous estimerons plutôt la moyenne et l'écart-type :
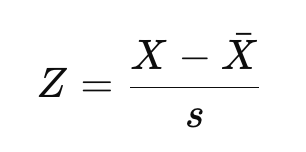
Ici, X-bar est la moyenne de l'échantillon et s est l'écart-type de l'échantillon.
Le résultat serait le même si vous utilisiez la moyenne et l'écart-type du nouvel ensemble de données normalisé. Mais il arrive que les chercheurs souhaitent comparer les données par rapport à une population de référence plus large en utilisant plutôt une moyenne et un écart-type de référence.
Imaginez que vous examiniez un ensemble de données sur le revenu, qui serait asymétrique à droite, et que vous fassiez une transformation logarithmique pour le normaliser. Dans ce cas, nous utiliserons la moyenne et l'écart-type nationaux au lieu de ceux de notre échantillon pour calculer les Z-scores. L'objectif est de permettre une comparaison significative entre les ensembles de données ou les études.
Par conséquent, si vous utilisez un échantillon, vous obtenez techniquement une approximation normale standardisée plutôt que la distribution normale standard théorique exacte. Je pense que cette distinction mérite d'être clarifiée, même si la différence doit être faible pour les grands ensembles de données.
Visualisation de la distribution normale standard
Voici une façon de créer une distribution normale standard théorique dans le langage de programmation R. Dans ce code, j'ai également ajouté des lignes verticales pour les scores standard, également appelés scores Z, qui est un moyen de nous indiquer, pour une valeur donnée, combien d'écarts types se situent au-dessus ou au-dessous de la moyenne de la population.
install.packages("ggplot2")
library(ggplot2)
ggplot(data.frame(x = c(-4, 4)), aes(x)) +
stat_function(fun = dnorm, geom = "area", fill = '#ffe6b7', color = 'black', alpha = 0.5, args = list( mean = 0, sd = 1)) +
labs(title = "Standard Normal Distribution", subtitle = "Standard Deviations and Z-Scores") +
theme(plot.title = element_text(hjust = 0.5, face = "bold")) +
theme(plot.subtitle = element_text(hjust = 0.5)) +
geom_vline(xintercept = 1, linetype = 'dotdash', color = "black") +
geom_vline(xintercept = -1, linetype = 'dotdash', color = "black") +
geom_vline(xintercept = 2, linetype = 'dotdash', color = "black") +
geom_vline(xintercept = -2, linetype = 'dotdash', color = "black") +
geom_vline(xintercept = 3, linetype = 'dotdash', color = "black") +
geom_vline(xintercept = -3, linetype = 'dotdash', color = "black") +
geom_text(aes(x=1, label="\n 1 σ", y=0.125), colour="#376795", angle=90, text=element_text(size=11)) +
geom_text(aes(x=2, label="\n 2 σ", y=0.125), colour="#376795", angle=90, text=element_text(size=11)) +
geom_text(aes(x=3, label="\n 3 σ", y=0.125), colour="#376795", angle=90, text=element_text(size=11)) +
geom_text(aes(x=-1, label="\n-1 σ", y=0.125), colour="#376795", angle=90, text=element_text(size=11)) +
geom_text(aes(x=-2, label="\n-2 σ", y=0.125), colour="#376795", angle=90, text=element_text(size=11)) +
geom_text(aes(x=-3, label="\n-3 σ", y=0.125), colour="#376795", angle=90, text=element_text(size=11))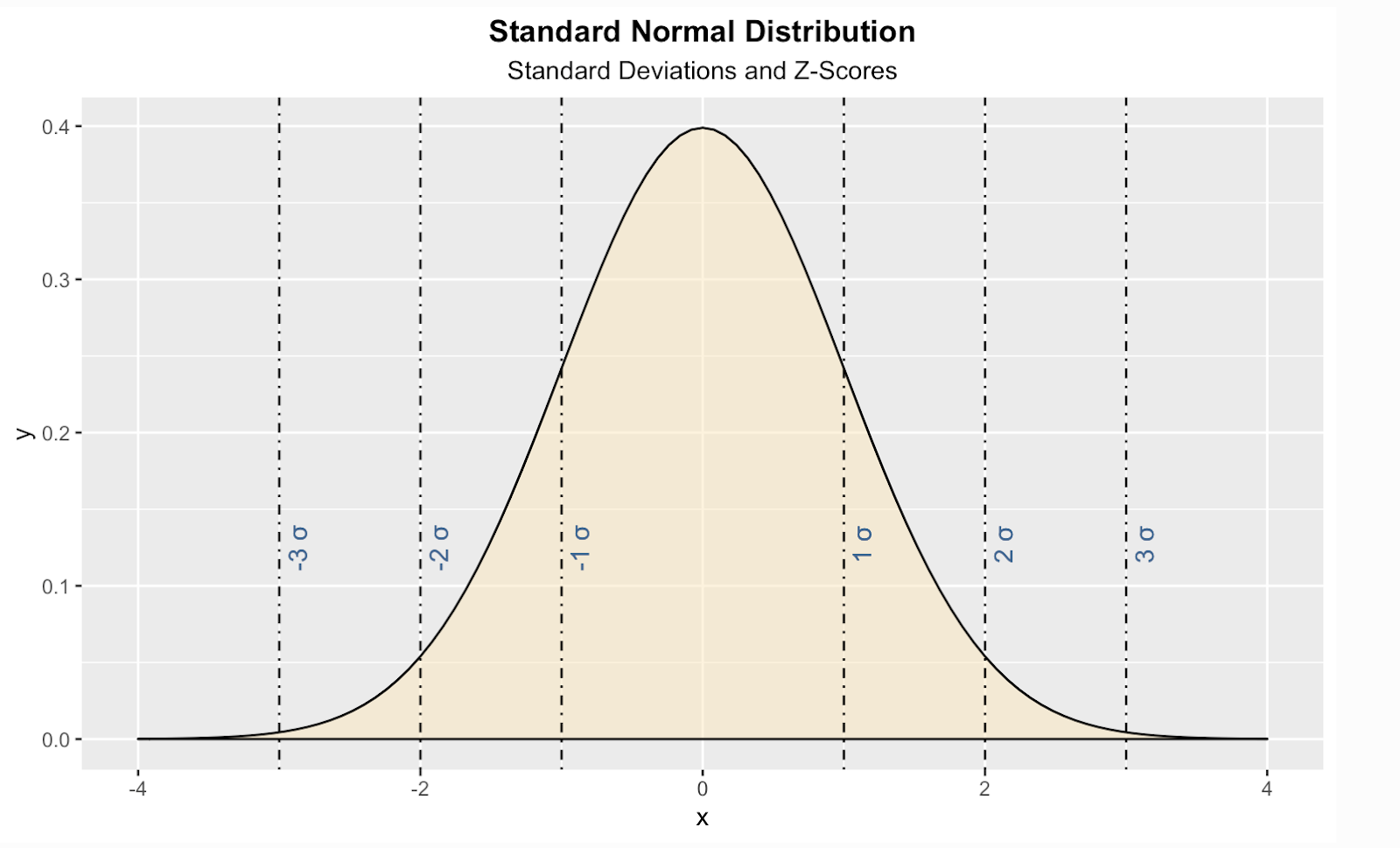
Vous devez savoir qu'il existe des distributions similaires qui peuvent ressembler à la normale standard mais qui n'en sont pas :
| Distribution | Pourquoi ce n'est pas normal |
|---|---|
| Distribution t | Queues légèrement plus lourdes, en fonction des degrés de liberté |
| Distribution logistique | Queues légèrement plus lourdes que la normale, forme différente |
| Distribution de Laplace | Pic plus net, queues plus lourdes, décroissance exponentielle |
La distribution normale standard et le tableau normal standard
Permettez-moi de revenir sur un point que j'ai mentionné précédemment : l'idée d'un tableau normal standard, également appelé tableau des scores Z, ou tableau Z, qui est utilisé pour trouver les probabilités cumulées pour un score Z, qui représente le nombre d'écarts types d'une valeur par rapport à la moyenne dans une distribution normale standard. Ce tableau est couramment utilisé en statistique pour les tests d'hypothèse, les intervalles de confiance et les calculs de probabilité. L'idée ici est qu'au lieu de calculer les probabilités manuellement, vous pouvez vous référer au tableau pour déterminer rapidement la proportion de valeurs qui se situent en dessous d'un score Z donné.
La lecture du tableau demande un peu d'entraînement et les tableaux sont parfois différents les uns des autres. Ici, vous le voyez structuré dans un format bidimensionnel. L'objectif est de faciliter la recherche de probabilités pour les scores Z lorsque l'on travaille avec des décimales. Dans ce cas, la colonne la plus à gauche contient le nombre entier et la première décimale du Z-score. La ligne supérieure représente la deuxième décimale. Pour trouver la probabilité associée à un score Z spécifique, recherchez la ligne correspondant à la première partie du score Z, puis la colonne correspondant à la deuxième décimale. La valeur à l'intersection de cette ligne et de cette colonne est la probabilité cumulée, c'est-à-dire la proportion de points de données qui se situent en dessous de ce score Z.
Il est préférable de montrer un exemple : Par exemple, supposons que vous calculiez un score Z de 0,32 pour les résultats d'un élève à un test. Cela signifie que le score se situe à 0,32 écart-type au-dessus de la moyenne. Utilisons maintenant le tableau Z pour trouver la probabilité qu'une valeur choisie au hasard soit inférieure à ce score Z.
- Étape 1 : Repérez la ligne correspondant à 0,3.
- Étape 2 : Repérez la colonne correspondant à 0,02.
- Étape 3 : Regardez l'intersection de la ligne pour 0,3 et de la colonne pour 0,02. La valeur à cette position est de 0,6915.
La probabilité cumulée pour Z = 0,32 est de 0,6554, ce qui signifie que 65,54 % des valeurs d'une distribution normale standard sont inférieures à 0,32 écart-type au-dessus de la moyenne. Si vous devez déterminer la probabilité qu'une valeur soit supérieure à un score Z donné, soustrayez la valeur du tableau de 1 avant de trouver la ligne et la colonne.
| Z | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 | 0.07 | 0.08 | 0.09 |
|---|---|---|---|---|---|---|---|---|---|
| 0.1 | 0.5793 | 0.6179 | 0.6554 | 0.6915 | 0.7257 | 0.7580 | 0.7881 | 0.8159 | 0.8413 |
| 0.2 | 0.6179 | 0.6554 | 0.6915 | 0.7257 | 0.7580 | 0.7881 | 0.8159 | 0.8413 | 0.8643 |
| 0.3 | 0.6554 | 0.6915 | 0.7257 | 0.7580 | 0.7881 | 0.8159 | 0.8413 | 0.8643 | 0.8849 |
| 0.4 | 0.6915 | 0.7257 | 0.7580 | 0.7881 | 0.8159 | 0.8413 | 0.8643 | 0.8849 | 0.9032 |
| 0.5 | 0.7257 | 0.7580 | 0.7881 | 0.8159 | 0.8413 | 0.8643 | 0.8849 | 0.9032 | 0.9192 |
| 0.6 | 0.7580 | 0.7881 | 0.8159 | 0.8413 | 0.8643 | 0.8849 | 0.9032 | 0.9192 | 0.9332 |
| 0.7 | 0.7881 | 0.8159 | 0.8413 | 0.8643 | 0.8849 | 0.9032 | 0.9192 | 0.9332 | 0.9452 |
| 0.8 | 0.8159 | 0.8413 | 0.8643 | 0.8849 | 0.9032 | 0.9192 | 0.9332 | 0.9452 | 0.9554 |
| 0.9 | 0.8413 | 0.8643 | 0.8849 | 0.9032 | 0.9192 | 0.9332 | 0.9452 | 0.9554 | 0.9641 |
| 1.0 | 0.8643 | 0.8849 | 0.9032 | 0.9192 | 0.9332 | 0.9452 | 0.9554 | 0.9641 | 0.9713 |
Conclusion
J'espère que vous avez apprécié cette exploration de la distribution normale standard. Continuez à apprendre avec nous ici à DataCamp. J'ai mentionné notre cours Introduction aux statistiques en R et notre cursus de compétences Inférence statistique en R. Mais si vous préférez Python, notre cours Pensée statistique en Python et notre cours Conception expérimentale en Python sont tous deux d'excellentes options.

Je suis rédacteur et éditeur dans le domaine de la science des données. Je suis particulièrement intéressé par l'algèbre linéaire, les statistiques, R, etc. Je joue également beaucoup aux échecs !
FAQ sur la distribution normale standard
En quoi la distribution normale standard diffère-t-elle d'une distribution normale ?
La distribution normale standard est un cas particulier de la distribution normale où la moyenne est de 0 et l'écart-type de 1. Cette normalisation facilite le calcul des probabilités et les comparaisons entre les ensembles de données.
La soustraction de la moyenne et la division par l'écart-type créent-elles une distribution normale standard ?
La soustraction de la moyenne et la division par l'écart-type transforment un ensemble de données sous une forme normalisée, mais ne créent pas nécessairement une distribution normale standard, à moins que les données d'origine ne soient normalement distribuées.
Quelle est la relation entre la distribution normale standard et le théorème de la limite centrale ?
Le théorème de la limite centrale stipule que la somme de plusieurs variables aléatoires indépendantes et identiquement distribuées tend à suivre une distribution normale, qui peut être normalisée sous la forme normale standard.
Que représente un score Z dans la distribution normale standard ?
Le score Z indique le nombre d'écarts types d'une valeur par rapport à la moyenne. Un score Z positif signifie que la valeur est supérieure à la moyenne, tandis qu'un score Z négatif signifie qu'elle est inférieure.
Quel est le lien entre la distribution normale standard et les intervalles de confiance ?
Les intervalles de confiance utilisent les scores Z pour déterminer les intervalles de probabilité pour l'estimation des paramètres de la population. Par exemple, un intervalle de confiance de 95 % correspond à des scores Z d'environ ±1,96.