- Data Science Use Case in Banking: Detecting Fraud
- Preparing the Dataset
- Calculating Fraud in the Dataset
- Using SMOTE to Re-Balance the Data
- Applying Logistic Regression
- Conclusion
Banking is one of those lucky fields where historically a lot of structured data is collected, and also one of the first where data science technologies were applied.
How is data science used in banking? Nowadays, data has become the most valuable asset in this sphere. Data science is a necessary requirement for banks to keep up with their rivals, attract more clients, increase the loyalty of existing clients, make more efficient data-driven decisions, empower their business, enhance operational efficiency, improve existing services/products and introduce new ones, reinforce security, and, as a result of all these actions, obtain more revenue. It is not surprising that the majority of all data science job demand comes from banking.
Data science allows the banking industry to successfully perform numerous tasks, including:
- investment risk analysis
- customer lifetime value prediction
- customer segmentation
- customer churn rate prediction
- personalized marketing
- customer sentiment analysis
- virtual assistants and chatbots
Below, we'll take a closer look at one of the most common data science use cases in banking.
Data Science Use Case in Banking: Detecting Fraud
Fraudulent activities represent a challenging problem not only in banking but also in many other spheres, such as government, insurance, public sector, sales, and healthcare. Any business that deals with a high number of online transactions runs a significant risk of fraud. Financial crimes can take various forms, including fraudulent credit card transactions, forged bank checks, tax evasion, money laundering, cyber attacks, customer account theft, synthetic identities, fake applications, and scams.
Fraud detection is a set of proactive measures undertaken to identify and prevent fraudulent activities and financial losses. Its main analytical techniques can be divided into two groups:
- Statistical: statistical parameter calculation, regression, probability distributions, data matching
- Artificial intelligence (AI): data mining, machine learning, deep learning
Machine learning represents an essential pillar for fraud detection. Its toolkit provides two approaches:
- Supervised methods: k-nearest neighbors, logistic regression, support vector machines, decision tree, random forest, time-series analysis, neural networks, etc.
- Unsupervised methods: cluster analysis, link analysis, self-organizing maps, principal component analysis, anomaly recognition, etc.
There is no universal and reliable machine learning algorithm for fraud detection. Instead, for the real-world data science use cases, several techniques or their combinations are usually tested, the model predictive accuracy is calculated, and the optimal approach is selected.
The main challenge for fraud detection systems is to rapidly adapt to constantly changing fraud patterns and fraudsters' tactics and to promptly uncover new and increasingly elaborate schemes. Fraud cases are always in a minority and are well concealed among the real transactions.
Preparing the Dataset
Let's explore a machine learning implementation of credit card fraud detection using Python programming language. We'll work on the creditcard_data dataset, which is a modified sample from a Kaggle dataset on Credit Card Fraud Detection. The original data represents transactions made on credit cards owned by European cardholders in two days in September 2013.
Let's import the data and take a quick look at it:
import pandas as pd
creditcard_data = pd.read_csv('creditcard_data.csv', index_col=0)
print(creditcard_data.info())
print('\n')
pd.options.display.max_columns = len(creditcard_data)
print(creditcard_data.head(3))<class 'pandas.core.frame.DataFrame'>
Int64Index: 5050 entries, 0 to 5049
Data columns (total 30 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 V1 5050 non-null float64
1 V2 5050 non-null float64
2 V3 5050 non-null float64
3 V4 5050 non-null float64
4 V5 5050 non-null float64
5 V6 5050 non-null float64
6 V7 5050 non-null float64
7 V8 5050 non-null float64
8 V9 5050 non-null float64
9 V10 5050 non-null float64
10 V11 5050 non-null float64
11 V12 5050 non-null float64
12 V13 5050 non-null float64
13 V14 5050 non-null float64
14 V15 5050 non-null float64
15 V16 5050 non-null float64
16 V17 5050 non-null float64
17 V18 5050 non-null float64
18 V19 5050 non-null float64
19 V20 5050 non-null float64
20 V21 5050 non-null float64
21 V22 5050 non-null float64
22 V23 5050 non-null float64
23 V24 5050 non-null float64
24 V25 5050 non-null float64
25 V26 5050 non-null float64
26 V27 5050 non-null float64
27 V28 5050 non-null float64
28 Amount 5050 non-null float64
29 Class 5050 non-null int64
dtypes: float64(29), int64(1)
memory usage: 1.2 MB
V1 V2 V3 V4 V5 V6 V7 \
0 1.725265 -1.337256 -1.012687 -0.361656 -1.431611 -1.098681 -0.842274
1 0.683254 -1.681875 0.533349 -0.326064 -1.455603 0.101832 -0.520590
2 1.067973 -0.656667 1.029738 0.253899 -1.172715 0.073232 -0.745771
V8 V9 V10 V11 V12 V13 V14 \
0 -0.026594 -0.032409 0.215113 1.618952 -0.654046 -1.442665 -1.546538
1 0.114036 -0.601760 0.444011 1.521570 0.499202 -0.127849 -0.237253
2 0.249803 1.383057 -0.483771 -0.782780 0.005242 -1.273288 -0.269260
V15 V16 V17 V18 V19 V20 V21 \
0 -0.230008 1.785539 1.419793 0.071666 0.233031 0.275911 0.414524
1 -0.752351 0.667190 0.724785 -1.736615 0.702088 0.638186 0.116898
2 0.091287 -0.347973 0.495328 -0.925949 0.099138 -0.083859 -0.189315
V22 V23 V24 V25 V26 V27 V28 \
0 0.793434 0.028887 0.419421 -0.367529 -0.155634 -0.015768 0.010790
1 -0.304605 -0.125547 0.244848 0.069163 -0.460712 -0.017068 0.063542
2 -0.426743 0.079539 0.129692 0.002778 0.970498 -0.035056 0.017313
Amount Class
0 189.00 0
1 315.17 0
2 59.98 0 The dataset contains the following variables:
- Numerically encoded variables V1 to V28 which are the principal components obtained from a PCA transformation. Due to confidentiality issues, no background information about the original features was provided.
- The Amount variable represents the transaction amount.
- The Class variable shows whether the transaction was a fraud (1) or not (0).
By their nature, fraud occurrences are fortunately an extreme minority in any list of transactions. However, machine learning algorithms usually work best when the different classes contained in the dataset are more or less equally present. Otherwise, there's little data to learn from. This problem is called the class imbalance.
Calculating Fraud in the Dataset
Let's calculate the percentage of fraudulent transactions over the total number of transactions in our dataset:
round(creditcard_data['Class'].value_counts()*100/len(creditcard_data)).convert_dtypes()0 99
1 1
Name: Class, dtype: Int64and create a plot to visualize the fraud to non-fraud data points:
import matplotlib.pyplot as plt
import numpy as np
def prep_data(df):
X = df.iloc[:, 1:28]
X = np.array(X).astype(float)
y = df.iloc[:, 29]
y = np.array(y).astype(float)
return X, y
def plot_data(X, y):
plt.scatter(X[y==0, 0], X[y==0, 1], label='Class #0', alpha=0.5, linewidth=0.15)
plt.scatter(X[y==1, 0], X[y==1, 1], label='Class #1', alpha=0.5, linewidth=0.15, c='r')
plt.legend()
return plt.show()
X, y = prep_data(creditcard_data)
plot_data(X, y)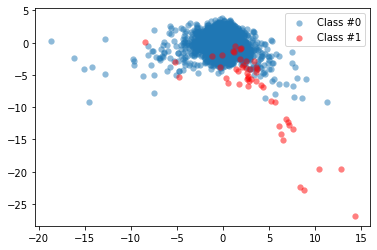
Using SMOTE to Re-Balance the Data
We can confirm now that the ratio of fraudulent transactions is very low and that we have a case of the class imbalance problem. To fix it, we can re-balance our data using the synthetic minority oversampling technique (SMOTE). Unlike random oversampling, SMOTE is slightly more sophisticated since it doesn't just create exact copies of observations. Instead, it uses characteristics of nearest neighbors of fraud cases to create new, synthetic samples that are quite similar to the existing observations in the minority class. Let's apply SMOTE to our credit card data:
from imblearn.over_sampling import SMOTE
method = SMOTE()
X_resampled, y_resampled = method.fit_resample(X, y)
plot_data(X_resampled, y_resampled)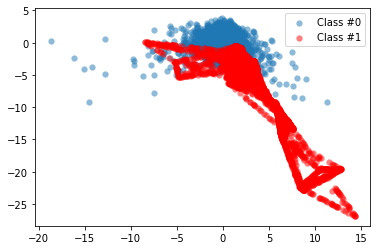
As we can see, using SMOTE suddenly gives us more observations of the minority class. To see the results of this approach even better, we'll compare them to the original data:
def compare_plot(X, y, X_resampled, y_resampled, method):
f, (ax1, ax2) = plt.subplots(1, 2)
c0 = ax1.scatter(X[y==0, 0], X[y==0, 1], label='Class #0',alpha=0.5)
c1 = ax1.scatter(X[y==1, 0], X[y==1, 1], label='Class #1',alpha=0.5, c='r')
ax1.set_title('Original set')
ax2.scatter(X_resampled[y_resampled==0, 0], X_resampled[y_resampled==0, 1], label='Class #0', alpha=.5)
ax2.scatter(X_resampled[y_resampled==1, 0], X_resampled[y_resampled==1, 1], label='Class #1', alpha=.5,c='r')
ax2.set_title(method)
plt.figlegend((c0, c1), ('Class #0', 'Class #1'), loc='lower center', ncol=2, labelspacing=0.)
plt.tight_layout(pad=3)
return plt.show()
print(f'Original set:\n'
f'{pd.value_counts(pd.Series(y))}\n\n'
f'SMOTE:\n'
f'{pd.value_counts(pd.Series(y_resampled))}\n')
compare_plot(X, y, X_resampled, y_resampled, method='SMOTE')Original set:
0.0 5000
1.0 50
dtype: int64
SMOTE:
0.0 5000
1.0 5000
dtype: int64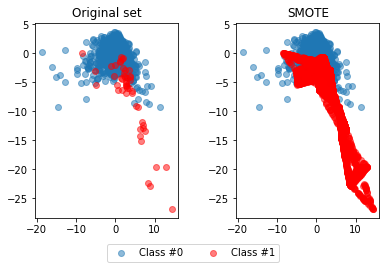
Hence, the SMOTE method has balanced our data completely, and the minority class is now equal in size to the majority class.
We'll return to the practical application of the SMOTE method soon, but for now, let's come back to the original data and try to detect the fraud cases. Following the "old-school" way, we have to create some rules to catch fraud. Such rules can concern, for example, unusual locations of transactions or suspiciously frequent transactions. The idea is to define threshold values based on common statistics, often on the mean values of observations, and use those thresholds on our features to detect fraud.
print(creditcard_data.groupby('Class').mean().round(3)[['V1', 'V3']]) V1 V3
Class
0 0.035 0.037
1 -4.985 -7.294In our particular case, let's apply the following conditions: V1 < -3 and V3 < -5. Then, to estimate the performance of this approach, we'll compare the flagged fraud cases to the actual ones:
creditcard_data['flag_as_fraud'] = np.where(np.logical_and(creditcard_data['V1']<-3, creditcard_data['V3']<-5), 1, 0)
print(pd.crosstab(creditcard_data['Class'], creditcard_data['flag_as_fraud'], rownames=['Actual Fraud'], colnames=['Flagged Fraud']))Flagged Fraud 0 1
Actual Fraud
0 4984 16
1 28 22Applying Logistic Regression
We detected 22 out of 50 fraud cases, but can't detect the other 28, and got 16 false positives. Let's see if using machine learning techniques can beat those results.
We're now going to implement a simple logistic regression classification algorithm on our credit card data to identify fraudulent occurrences and then visualize the results on a confusion matrix:
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
lr = LogisticRegression()
lr.fit(X_train, y_train)
predictions = lr.predict(X_test)
print(pd.crosstab(y_test, predictions, rownames=['Actual Fraud'], colnames=['Flagged Fraud']))Flagged Fraud 0.0 1.0
Actual Fraud
0.0 1504 1
1.0 1 9It's important to note that here we have fewer observations to look at in the confusion matrix because we're only using the test set to calculate the model results on, i.e., only 30% of the whole dataset.
We caught a higher percentage of fraud cases: 90% (9 out of 10), compared to the previous result of 44% (22 out of 50). We also got far fewer false positives than before, so that's an improvement.
Let's now return to the class imbalance problem discussed earlier and explore whether we can enhance the prediction results even further by combining the logistic regression model with the SMOTE resampling method. To do it efficiently and in one go, we need to define a pipeline and run it on our data:
from imblearn.pipeline import Pipeline
# Defining which resampling method and which ML model to use in the pipeline
resampling = SMOTE()
lr = LogisticRegression()
pipeline = Pipeline([('SMOTE', resampling), ('Logistic Regression', lr)])
pipeline.fit(X_train, y_train)
predictions = pipeline.predict(X_test)
print(pd.crosstab(y_test, predictions, rownames=['Actual Fraud'], colnames=['Flagged Fraud']))Flagged Fraud 0.0 1.0
Actual Fraud
0.0 1496 9
1.0 1 9As we can see, in our case the SMOTE didn't bring any improvements: we still caught 90% of fraud occurrences and, moreover, we have a slightly higher number of false positives. The explanation here is that resampling doesn’t necessarily lead to better results in all cases. When the fraud cases are very spread out over the data, their nearest neighbors aren't necessarily also fraud cases, so using SMOTE can introduce a bias.
Conclusion
As a possible way forward, to increase the logistic regression model accuracy, we can tune some of the algorithm parameters. K-fold cross-validation can also be considered instead of just splitting the dataset into two parts. Finally, we can try some other machine learning algorithms (e.g., decision tree or random forest) and see if they give better results.
If you want to learn more about the theoretical and technical aspects of fraud detection model implementation, you can explore the materials of the Fraud Detection in Python course.


