Matriz Singular: Principais conceitos e exemplos em ciência de dados

Uma matriz singular é uma matriz quadrada que não pode ser invertida, o que significa que ela não tem inversa multiplicativa. Esse conceito fundamental da álgebra linear tem um imenso impacto nos aplicativos de ciência de dados, desde algoritmos de machine learning até a estabilidade numérica em métodos computacionais.

Neste artigo, definiremos o que torna uma matriz singular e exploraremos suas propriedades e características matemáticas. Em seguida, examinaremos os métodos de detecção de matrizes singulares. Entenderemos suas implicações reais na ciência de dados e aprenderemos a lidar com elas de forma eficaz.

O que é uma matriz singular?

Uma matriz singular é uma matriz quadrada cujo determinante é igual a zero, o que a torna não-inversível. 

Em termos matemáticos, para uma matriz quadrada A, se det(A) = 0, então A é singular e não tem matriz inversa A-¹.

A característica fundamental de uma matriz singular é que suas linhas ou colunas são linearmente dependentes, o que significa que pelo menos uma linha (ou coluna) pode ser expressa como uma combinação linear das outras linhas (ou colunas). Essa dependência cria uma "deficiência" na matriz que impede que ela tenha uma inversa única.

Outra maneira de entender as matrizes singulares é por meio de sua classificação. Uma matriz quadrada é singular se e somente se sua classificação for menor que o número de linhas (ou colunas). A classificação representa o número máximo de linhas ou colunas linearmente independentes, portanto, quando isso fica aquém das dimensões da matriz, ocorre a singularidade.

Esse conceito é importante porque muitos algoritmos dependem da inversão de matrizes, desde a solução de problemas de regressão linear até a implementação de determinadas técnicas de machine learning. Quando uma matriz é singular, essas operações falham, exigindo abordagens alternativas ou etapas de pré-processamento para lidar com a situação.

Propriedades e condições de matrizes singulares

Compreender as propriedades matemáticas das matrizes singulares ajuda a identificar possíveis problemas antes que eles causem problemas computacionais nos fluxos de trabalho da ciência de dados.

• Zero determinant: O determinante de uma matriz singular é sempre igual a zero, indicando diretamente a não-invertibilidade. Esse determinante zero significa que a transformação da matriz não é bijetiva, permitindo que vários vetores de entrada sejam mapeados para a mesma saída.
• Dependência linear: As matrizes singulares contêm linhas ou colunas linearmente dependentes, em que pelo menos uma linha pode ser expressa como uma combinação linear das outras. Essa dependência cria informações redundantes que levam a desafios computacionais.
• Deficiência de classificação: Uma matriz n×n singular tem classificação menor que n, possuindo menos linhas ou colunas linearmente independentes do que sua dimensão. Essa deficiência explica por que os sistemas que envolvem matrizes singulares não têm soluções únicas.
• Autovalores zero: Pelo menos um autovalor de uma matriz singular é exatamente zero, correspondendo a direções no espaço que são completamente colapsadas durante a transformação. O número de autovalores zero é igual à nulidade da matriz.
• Espaço nulo não trivial: As matrizes singulares têm vetores diferentes de zero que, quando multiplicados pela matriz, produzem o vetor zero. A dimensão desse espaço nulo indica a quantidade de informações perdidas durante a transformação.

Agora que entendemos as propriedades fundamentais de uma matriz singular, vamos compará-las com as matrizes não-singulares.

Singular vs. Matriz não-singular

As matrizes não-singulares são invertíveis e suportam cálculos numéricos confiáveis, enquanto as matrizes singulares não têm inversos e exigem um tratamento especializado. Essa divisão fundamental determina a viabilidade computacional dos aplicativos de ciência de dados. 

Essas diferenças se aplicam a cada uma das propriedades fundamentais de uma matriz singular que vimos anteriormente. A tabela abaixo resume as diferenças entre as matrizes singulares e não-singulares:

Exemplos de matrizes singulares

O exame de exemplos específicos ajuda a ilustrar como a singularidade se manifesta na prática e desenvolve a intuição para o reconhecimento dessas matrizes.

Matriz singular simples 2×2

Considere este exemplo básico em que uma linha é um múltiplo de outra:

Matriz singular 2×2 simples (Imagem do autor)

Aqui, a segunda linha é exatamente a metade da primeira linha, criando uma dependência linear. O determinante é (2×2) - (4×1) = 0, confirmando a singularidade.

Zero linha ou coluna

Qualquer matriz que contenha uma linha ou coluna de todos os zeros é automaticamente singular:

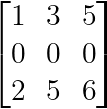
Zero linha ou coluna (Imagem do autor)

A linha zero impossibilita que a matriz tenha classificação completa, independentemente das outras entradas.

Linhas ou colunas idênticas

As matrizes com linhas ou colunas idênticas são sempre singulares:

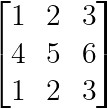
Linhas ou colunas idênticas (Imagem do autor)

A primeira e a terceira linhas são idênticas, criando uma dependência linear perfeita.

Dependência de combinação linear

Uma singularidade mais sutil ocorre quando uma linha é igual a uma combinação de outras:

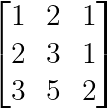
Dependência de combinação linear (Imagem do autor)

Aqui, a terceira linha é igual à soma das duas primeiras linhas: [3,5,2] = [1,2,1] + [2,3,1].

Cada um desses exemplos mostrados acima demonstra como matrizes aparentemente diferentes podem compartilhar a propriedade fundamental da dependência linear que define a singularidade.

Por que as matrizes singulares ocorrem na ciência de dados?

As matrizes singulares surgem com frequência em aplicativos de ciência de dados devido à natureza dos dados do mundo real e dos fluxos de trabalho analíticos comuns.

Multicolinearidade em conjuntos de recursos

A fonte mais comum de matrizes singulares na ciência de dados é a multicolinearidade, quando vários recursos em um conjunto de dados estão perfeitamente ou quase perfeitamente correlacionados. Isso cria uma dependência linear entre as colunas da matriz de design, levando à singularidade durante as operações da matriz.

Considere um conjunto de dados de varejo em que você tem recursos para total_sales, q1_sales, q2_sales, q3_sales e q4_sales. Se os valores de vendas trimestrais sempre somam exatamente o total de vendas, então:

total_sales = q1_sales + q2_sales + q3_sales + q4_sales

Quando essa relação se mantém perfeitamente em todas as observações, a matriz de design resultante se torna singular. Qualquer algoritmo de regressão linear que tente inverter essa matriz falhará porque uma coluna pode ser perfeitamente prevista a partir das outras.

Cenários semelhantes ocorrem com recursos derivados como:

• Temperatura em Celsius e Fahrenheit
• Idade e ano de nascimento (com um ano de referência fixo)
• Razões em que o numerador e o denominador também são características
• Variáveis fictícias que somam uma constante (a armadilha da variável fictícia)

Dados insuficientes relativos a recursos

Conjuntos de dados de alta dimensão com menos observações do que recursos produzem naturalmente matrizes singulares. Quando você tem n amostras, mas p recursos, em que p > n, a matriz de covariância n×n resultante ou a matriz grama terá classificação no máximo n, o que a torna singular se você precisar de uma matriz invertível p×p.

Essa "maldição da dimensionalidade" geralmente afeta:

• Dados genômicos com milhares de genes, mas centenas de amostras
• Análise de texto com grandes vocabulários, mas documentos limitados
• Processamento de imagens com recursos de alta resolução, mas com conjuntos de treinamento pequenos
• Modelagem financeira com muitos indicadores econômicos, mas com séries temporais curtas

Pré-processamento de dados 

As etapas comuns de pré-processamento de dados podem introduzir inadvertidamente a singularidade:

• Transformações de centralização: Centralizar cada recurso (subtraindo a média) não causa singularidade por si só, mas, na presença de outras dependências lineares, pode preservá-las ou enfatizá-las. Nos casos em que os recursos já são quase dependentes, a centralização pode aproximá-los da dependência exata com precisão limitada.
• Dimensionamento e normalização: Certas operações de escalonamento podem tornar as relações lineares sutis mais pronunciadas, levando recursos quase dependentes a uma dependência perfeita devido aos limites de precisão do ponto flutuante.
• Engenharia de recursos: A criação de recursos polinomiais, termos de interação ou expansões de base pode introduzir relações lineares inesperadas. Por exemplo, se você criar os recursos x, ^x² e ^2x²- x, o terceiro recurso(^2x²- x) será perfeitamente determinado pelos dois primeiros.

A compreensão dessas fontes comuns de singularidade permite que os cientistas de dados implementem medidas preventivas no início de seus fluxos de trabalho, como a verificação de multicolinearidade durante a análise exploratória de dados ou o uso proativo de técnicas de regularização.

Agora que entendemos por que as matrizes singulares ocorrem na ciência de dados, vamos explorar métodos práticos para detectá-las antes que causem falhas computacionais.

Como detectar matrizes singulares

A maneira mais direta de detectar uma matriz singular é verificando seu determinante. Se o determinante de uma matriz quadrada for zero, a matriz será singular e não-inversível. Esse método é simples, matematicamente sólido e amplamente utilizado na prática.

Vamos entender como você pode realizar essa verificação usando Python:

import numpy as np

# Example 2x2 matrix
A = np.array([[2, 4],
             [1, 2]])

# Calculate the determinant
det_A = np.linalg.det(A)

print(f"Determinant of A: {det_A}")

# Check if matrix is singular
if np.isclose(det_A, 0):
   print("Matrix A is singular.")
else:
   print("Matrix A is non-singular.")

No exemplo acima, definimos uma matriz A2×2 e usamos o sitenp.linalg.det() para calcular seu determinante. Como a aritmética de ponto flutuante pode introduzir pequenos erros numéricos, usamos o site np.isclose() para verificar se o determinante é efetivamente zero. Se for, concluímos que a matriz é singular. 

Você verá o resultado abaixo confirmando a singularidade:

Matriz singular de detecção de saída. (Imagem do autor)

Esse método é intuitivo e prático, o que o torna uma primeira etapa confiável no diagnóstico de problemas relacionados à invertibilidade de matrizes em fluxos de trabalho de ciência de dados.

Como lidar com matrizes singulares na prática

Ao se deparar com matrizes singulares em fluxos de trabalho de ciência de dados, várias estratégias podem resolver os desafios computacionais e, ao mesmo tempo, preservar a integridade analítica.

Técnicas de regularização

A adição de pequenos valores à diagonal (regularização Ridge) é a abordagem mais comum para lidar com matrizes quase-singulares em problemas de regressão. Essa técnica transforma matrizes singulares em matrizes invertíveis, mantendo a estabilidade numérica:

# Ridge regularization approach
lambda_reg = 1e-6
A_regularized = A + lambda_reg * np.eye(A.shape[0])

Cálculo do pseudoinverso

O pseudoinverso de Moore-Penrose fornece um inverso generalizado para matrizes singulares, oferecendo a "melhor" solução em um sentido de mínimos quadrados:

# Using pseudoinverse for singular matrices
A_pinv = np.linalg.pinv(A)
x = A_pinv @ b 

Redução da dimensionalidade

A remoção de recursos linearmente dependentes elimina a singularidade emsua origem. A análise de componentes principais ouas técnicas de seleção de recursos podem identificar e remover dimensões redundantes:

# PCA-based dimensionality reduction
from sklearn.decomposition import PCA
pca = PCA(n_components=0.95) 
X_reduced = pca.fit_transform(X)

Algoritmos alternativos

Alguns algoritmos são projetados especificamente para lidar com matrizes singulares. A decomposição QR com pivotamento pode resolver sistemas lineares mesmo quando a matriz de coeficientes é singular, fornecendo soluções quando elas existem e identificando inconsistências quando não existem.

Essas estratégias garantem que as matrizes singulares não inviabilizem os projetos de ciência de dados, mantendo o rigor matemático e a interpretabilidade dos resultados.

Conclusão

Este artigo explorou as matrizes singulares, que aprendemos serem matrizes quadradas com determinantes zero que não podem ser invertidas devido a dependências lineares entre linhas ou colunas. Analisamos por que eles aparecem comumente na ciência de dados, desde a multicolinearidade e os dados de alta dimensão até os problemas introduzidos durante o pré-processamento. 

Neste artigo, também analisamos maneiras de detectar e lidar com matrizes singulares usando técnicas básicas como verificações de determinantes, regularização, pseudoinversos e redução de dimensionalidade. (Se você ainda estiver interessado em pesquisar por conta própria, ferramentas como a análise do número de condição ou a decomposição do valor singular podem oferecer ainda mais informações sobre o comportamento da matriz e a estabilidade numérica).

Para aprofundar seu conhecimento sobre álgebra linear e sua função fundamental nos aplicativos de ciência de dados, inscreva-se em nosso curso Álgebra linear para ciência de dados, no qual você dominará esses conceitos fundamentais e suas implementações em cenários do mundo real.