Teste de hipóteses facilitado

O teste de hipóteses é uma parte fundamental da estatística que ajuda você a tomar decisões informadas em uma ampla variedade de campos - desde medicina até economia e ciências sociais. Este guia o guiará pelos principais conceitos, tipos, etapas e aplicações reais dos testes de hipóteses, garantindo que você possa interpretar e apresentar suas descobertas estatísticas com confiança.

Se você estiver pronto para aprender mais sobre testes de hipóteses, selecione o curso que corresponde à sua tecnologia preferida: Teste de hipóteses em Python, Teste de hipóteses em R ou Introdução à estatística no Google Sheets. Além disso, faça nosso curso de Introdução à Estatística, que é independente de tecnologia.

O que é teste de hipótese?

O teste de hipóteses é um procedimento estatístico usado para testar suposições ou hipóteses sobre um parâmetro populacional. Envolve a formulação de uma hipótese nula (H0) e uma hipótese alternativa (Ha), a coleta de dados e a determinação de se as evidências são fortes o suficiente para rejeitar a hipótese nula.

O principal objetivo do teste de hipóteses é fazer inferências sobre uma população com base em uma amostra de dados. Ele permite que pesquisadores e analistas quantifiquem a probabilidade de que as diferenças ou relações observadas nos dados tenham ocorrido por acaso, em vez de refletir um efeito verdadeiro na população.

Etapas do teste de hipóteses

Vamos explicar a você como fazer um teste de hipótese, uma etapa de cada vez.

Etapa 1: Declare suas hipóteses

A primeira etapa é formular sua pergunta de pesquisa em duas hipóteses concorrentes:

1. Hipótese nula (H0): Essa é a suposição padrão de que não há efeito ou diferença.
2. Hipótese alternativa (Ha): Essa é a hipótese de que há um efeito ou diferença.

Por exemplo:

• H0: A altura média dos homens é igual à altura média das mulheres.
• Ha: A altura média dos homens não é igual à altura média das mulheres.

Etapa 2: Coletar e preparar dados

Colete dados por meio de experimentos, pesquisas ou estudos de observação. Assegure-se de que o método de coleta de dados seja projetado para testar a hipótese e seja representativo da população. Essa etapa geralmente envolve:

• Definição da população de interesse.
• Seleção de um método de amostragem adequado.
• Determinação do tamanho da amostra.
• Coleta e organização dos dados.

Etapa 3: Escolha o teste estatístico apropriado

Selecione um teste estatístico com base no tipo de dados e na hipótese. A escolha depende de fatores como:

• Tipo de dados (contínuos, categóricos, etc.)
• Distribuição dos dados (normal, não normal)
• Tamanho da amostra
• Número de grupos que estão sendo comparados

Os testes comuns incluem:

• Testes t (para comparação de médias)

• testes de qui-quadrado (para dados categóricos)

• ANOVA (para comparação de médias de vários grupos)

Etapa 4: Calcule a estatística de teste e o valor p

Use software estatístico ou fórmulas para calcular a estatística de teste e o valor p correspondente. Essa etapa quantifica o quanto os dados da amostra se desviam da hipótese nula.

O valor p é um conceito importante no teste de hipóteses. Representa a probabilidade de observar resultados tão extremos quanto os dados da amostra, supondo que a hipótese nula seja verdadeira.

Etapa 5: Tomar uma decisão

Compare o valor p com o nível de significância predeterminado (α), que normalmente é definido como 0,05. A regra de decisão é a seguinte:

• Se o valor de p for ≤ α: Rejeitar a hipótese nula, sugerindo que as evidências apóiam a hipótese alternativa.
• Se o valor de p > α: Não rejeitar a hipótese nula, sugerindo evidência insuficiente para apoiar a hipótese alternativa.

É importante observar que o fato de você não rejeitar a hipótese nula não prova que ela é verdadeira; significa apenas que não há evidências suficientes para concluir o contrário.

Etapa 6: Apresente suas descobertas

Informe os resultados, incluindo a estatística de teste, o valor p e a conclusão. Discuta se as descobertas apóiam a hipótese inicial e suas implicações. Ao apresentar os resultados, leve em consideração:

• Fornecimento de contexto para o estudo.
• Declarar claramente as hipóteses.
• Informar a estatística de teste e o valor p.
• Interpretação dos resultados em linguagem simples.
• Discutir o significado prático das descobertas.

Tipos de testes de hipóteses

Os testes de hipóteses podem ser categorizados em dois tipos principais:

Testes paramétricos

Os testes paramétricos pressupõem que os dados seguem uma distribuição de probabilidade específica, normalmente a distribuição normal. Em geral, esses testes são mais eficientes quando as premissas são atendidas. Os testes paramétricos comuns incluem:

• Testes t (uma amostra, amostras independentes, amostras emparelhadas)
• ANOVA (medidas unidirecionais, bidirecionais e repetidas)
• Testes Z (uma amostra, duas amostras)
• Testes F (unidirecional, bidirecional)

Testes não paramétricos

Os testes não paramétricos não pressupõem uma distribuição específica dos dados. Eles são úteis ao lidar com dados ordinais ou quando as suposições dos testes paramétricos são violadas. Os exemplos incluem:

• Teste U de Mann-Whitney
• Teste de classificação assinada de Wilcoxon
• Teste de Kruskal-Wallis

Selecionando o teste apropriado

Ao escolher um teste de hipótese, os pesquisadores consideram algumas categorias amplas:

1. Distribuição de dados: Determine se os dados são normalmente distribuídos, pois muitos testes pressupõem normalidade.
2. Número de grupos: Identifique quantos grupos você está comparando (por exemplo, um grupo, dois grupos ou mais).
3. Independência do grupo: Decida se seus grupos são independentes (sujeitos diferentes) ou dependentes (mesmos sujeitos medidos várias vezes).
4. Tipo de dados:
• Contínuo (por exemplo, altura, peso),
• Ordinal (por exemplo, classificações),
• Nominal (por exemplo, categorias sem ordem).

Com base nessas categorias, você pode selecionar o teste estatístico apropriado. Por exemplo, se os dados forem normalmente distribuídos e você tiver dois grupos independentes com dados contínuos, você usaria um teste t independente. Se seus dados não forem distribuídos normalmente com dois grupos independentes e dados ordinais, recomenda-se o teste U de Mann-Whitney.

Para ajudar a escolher o teste adequado, considere o uso de um fluxograma de teste de hipótese como um guia geral:

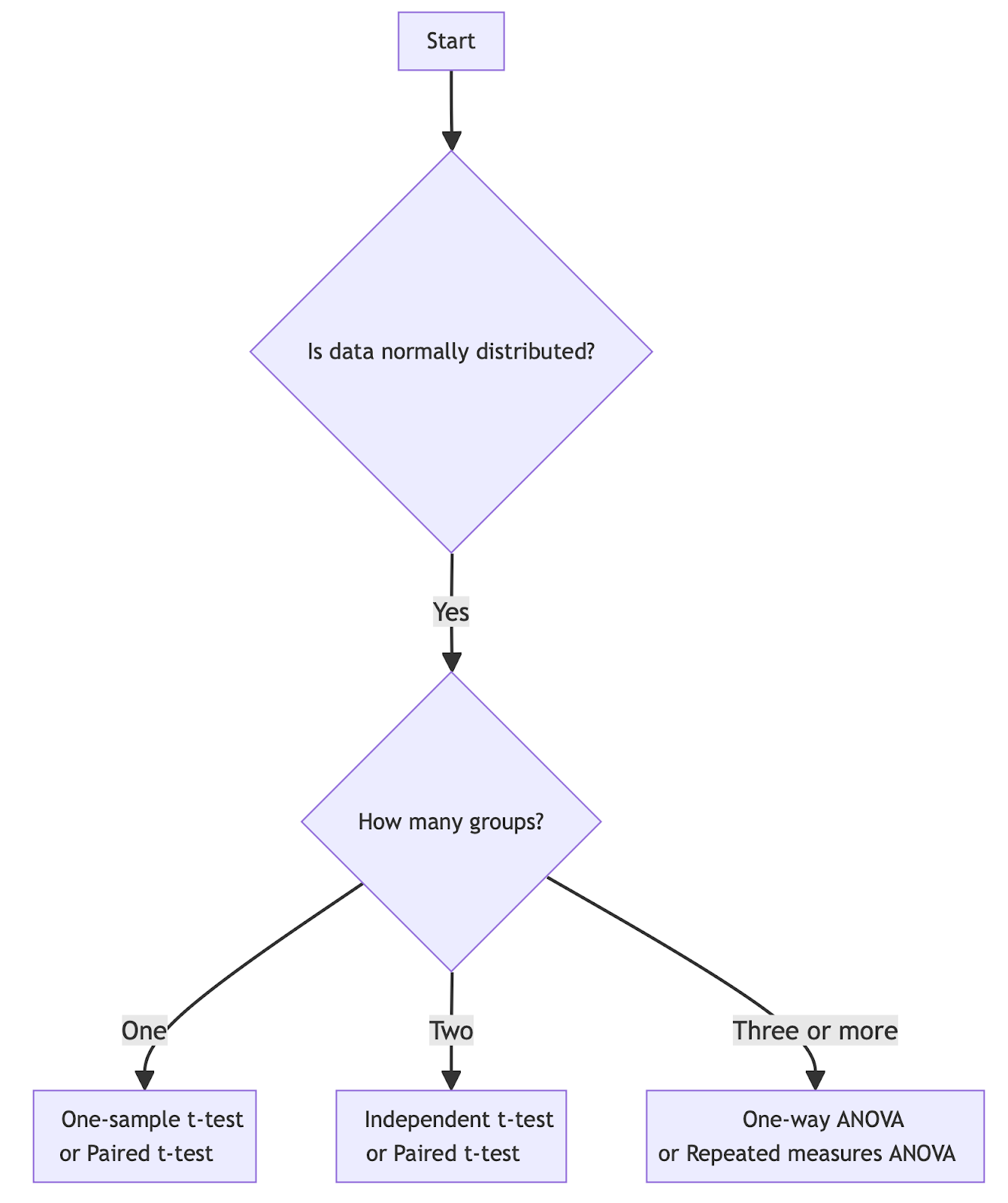
Escolha do teste de hipótese correto para dados normalmente distribuídos. Imagem do autor.

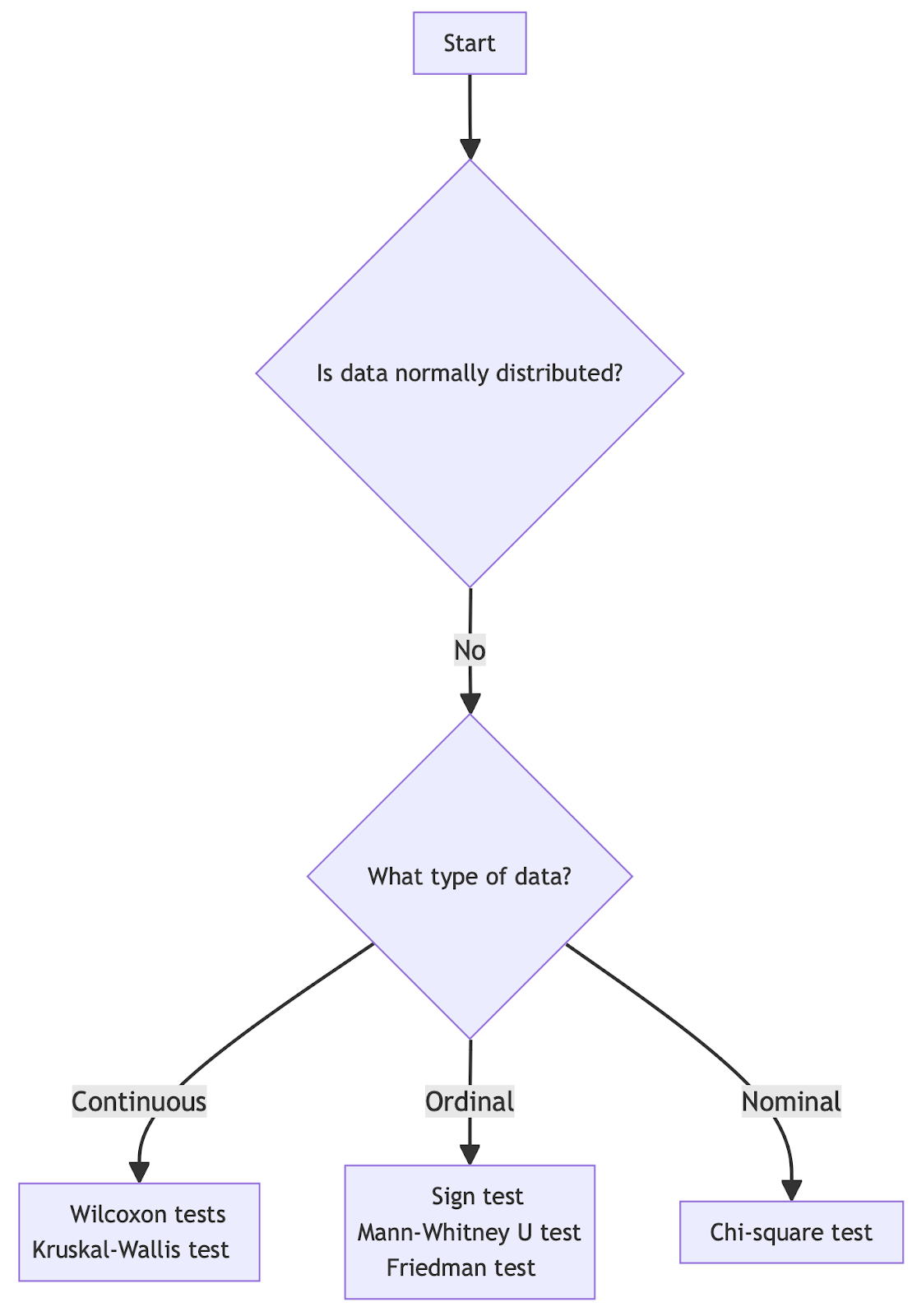
Escolhendo o teste de hipótese correto para dados distribuídos de forma não normal. Imagem do autor.

Abordagens modernas para testes de hipóteses

Além dos métodos tradicionais de teste de hipóteses, há várias abordagens modernas:

Testes de permutação ou randomização

Esses testes envolvem o embaralhamento aleatório dos dados observados muitas vezes para criar uma distribuição de resultados possíveis sob a hipótese nula. Eles são particularmente úteis ao lidar com amostras pequenas ou quando as suposições dos testes paramétricos não são atendidas.

Bootstrapping

O bootstrapping é uma técnica de reamostragem que envolve a amostragem repetida com substituição do conjunto de dados original. Ele pode ser usado para estimar a distribuição de amostragem de uma estatística e construir intervalos de confiança.

Simulação de Monte Carlo

Os métodos de Monte Carlo usam amostragem aleatória repetida para obter resultados numéricos. Nos testes de hipóteses, eles podem ser usados para estimar os valores p de modelos estatísticos complexos ou quando for difícil obter soluções analíticas.

Controle de erros

Ao realizar testes de hipóteses, é melhor entender e controlar os possíveis erros:

Erros do tipo I e do tipo II

• Erro do tipo I: Rejeitar a hipótese nula quando ela é realmente verdadeira (falso positivo).
• Erro do tipo II: Não rejeitar a hipótese nula quando ela é realmente falsa (falso negativo).

O nível de significância (α) controla diretamente a probabilidade de um erro do Tipo I. Diminuir α reduz a chance de erros do Tipo I, mas aumenta o risco de erros do Tipo II.

Para equilibrar esses erros:

1. Ajuste o nível de significância com base nas consequências de cada tipo de erro.
2. Aumentar o tamanho da amostra para melhorar o poder do teste.
3. Use testes unicaudais quando apropriado.

O efeito de gaveta de arquivo

O efeito gaveta de arquivo refere-se ao viés de publicação em que os estudos com resultados significativos têm maior probabilidade de serem publicados do que aqueles com resultados não significativos. Isso pode levar a uma superestimação dos efeitos na literatura. Para atenuar isso:

• Considere o pré-registro de estudos.
• Publique todos os resultados, significativos ou não.
• Conduzir meta-análises que levem em conta o viés de publicação.
• Simule os dados com antecedência.

Glossário de termos e definições importantes

• Hipótese nula (H0): O pressuposto padrão de que não há efeito ou diferença.
• Hipótese alternativa (Ha): A hipótese de que há um efeito ou diferença.
• Valor de p: A probabilidade de observar os resultados do teste sob a hipótese nula.
• Nível de significância (α): O limite para rejeitar a hipótese nula, geralmente definido como 0,05.
• Estatística de teste: Um valor padronizado usado para comparar os dados observados com a hipótese nula.
• Erro do tipo I: Rejeição de uma hipótese nula verdadeira (falso positivo).
• Erro do tipo II: Não rejeitar uma hipótese nula falsa (falso negativo).
• Poder estatístico: A probabilidade de rejeitar corretamente uma hipótese nula falsa.
• Intervalo de confiança: Um intervalo de valores que provavelmente contém o parâmetro verdadeiro da população.
• Tamanho do efeito: Uma medida da magnitude da diferença ou do relacionamento que está sendo testado.

Conclusão

Lembre-se de que o teste de hipótese é apenas uma parte do conjunto de ferramentas de inferência estatística. Sempre considere a importância prática de suas descobertas, não apenas a importância estatística. À medida que ganhar experiência, você desenvolverá um entendimento de quando e como aplicar essas técnicas em vários cenários do mundo real.

Para aprimorar ainda mais seu conhecimento estatístico, você pode explorar tópicos como How to Become a Statistician in 2024 (Como se tornar um estatístico em 2024), que oferece insights sobre o campo em evolução e as habilidades necessárias para o sucesso. Além disso, praticar as 35 principais perguntas e respostas de entrevistas de estatística para 2024 e trabalhar com nosso curso Practicing Statistics Interview Questions in R pode ajudar você a aprimorar suas habilidades e se preparar para as entrevistas.