Introdução a modelos não lineares e percepções usando o R

Este tutorial é uma contribuição valiosa de nossa comunidade e foi editado pela DataCamp para fins de clareza e precisão.

Tem interesse em compartilhar sua própria experiência? Gostaríamos muito de ouvir sua opinião! Sinta-se à vontade para enviar seus artigos ou ideias por meio de nosso Formulário de Contribuição da Comunidade.

Os modelos não lineares não são mais tão populares como antes. Atualmente, muitos livros pulam qualquer discussão sobre modelos não lineares ou os explicam de forma limitada. Aparentemente, há um bom número de motivos para isso. Em primeiro lugar, é possível ajustar uma curva não linear usando regressão linear por meio de termos polinomiais de ordem superior ou aplicando uma função de base (em outras palavras, aplicar uma transformação logarítmica ou sqrt nas variáveis explicativas). Em segundo lugar, pode-se escolher a simplicidade em vez de modelos complexos, pois os modelos lineares são fáceis de interpretar e explicar.

Além disso, para aplicar um modelo não linear, é importante visualizar os dados e ter uma noção da trajetória, o que não é possível em uma configuração multivariada. Por fim, os modelos não lineares são mais adequados para casos mecanicistas em que os fenômenos são puramente físicos ou em termos determinísticos, o que não é o caso do big data, em que as atividades do usuário são registradas por máquinas.

Entretanto, apesar de todos esses bons motivos, a modelagem não linear é uma bela ciência que deve ser explorada e comparada com sua contraparte linear.

Modelo de regressão não linear

As técnicas de estimativa de um modelo não linear são explicitamente iterativas. Além disso, há uma diferença fundamental na maneira como se aplica uma fórmula não linear, que não é a mesma que uma fórmula linear. Seguindo três equações/fórmulas diferentes, cada uma delas é considerada linear porque a relação entre a variável y e _B0, _B1 e _B2 é uma linha reta.

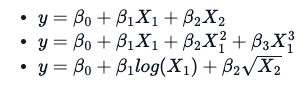
O que torna uma fórmula não linear é algo parecido com isto:

O uso de _B0 ou _B1 é arbitrário. Entretanto, as duas últimas equações não têm uma relação linear entre a variável y e _B0.

Infelizmente, isso torna os cálculos mais difíceis, e uma solução numérica bem-sucedida para o problema de estimativa não será garantida. Portanto, os modelos não lineares vêm com uma advertência de que a obtenção de respostas pode não ser intuitiva ou precisa.

Modelo especializado

Normalmente, quando se aplica um modelo não linear, são usados tipos especializados. Isso torna o ajuste de um modelo não linear mais conveniente ou numericamente mais fácil, mas precisa ser acordado por algum especialista no assunto e alinhado com os dados. Por tipos especializados, queremos dizer que um usa uma equação matemática predefinida. Aqui está a lista das equações não lineares usadas com mais frequência (algumas foram omitidas por questões de concisão).

Estratégia envolvida no modelo de regressão não linear

1. Visualize os dados para ver se uma função matemática especializada pode explicar melhor os dados.
2. Observando o gráfico ou usando uma função de autoinicialização (explicada abaixo), selecione os valores dos parâmetros iniciais.
3. Ajuste o modelo e examine-o.
4. Realize uma análise estatística do modelo ajustado para entender o intervalo de confiança do parâmetro, o erro residual e a variação explicada.
5. Tente adicionar mais parâmetros ao modelo se isso ajudar a reduzir o erro residual.
6. Sempre ajuste um modelo linear e compare os resultados de modelos não lineares e lineares.

Explicando o modelo não linear por meio de um exemplo

Vamos ajustar um modelo não linear especializado em um conjunto de dados popular, Puromycin, que apresenta a taxa de reação e as informações de concentração para uma reação enzimática envolvendo células com o medicamento Puromycin. Os dados foram obtidos com duas classes de células, uma tratada com o medicamento Puromycin e outra sem esse medicamento.

names(Puromycin)Puromycin'conc''rate''state'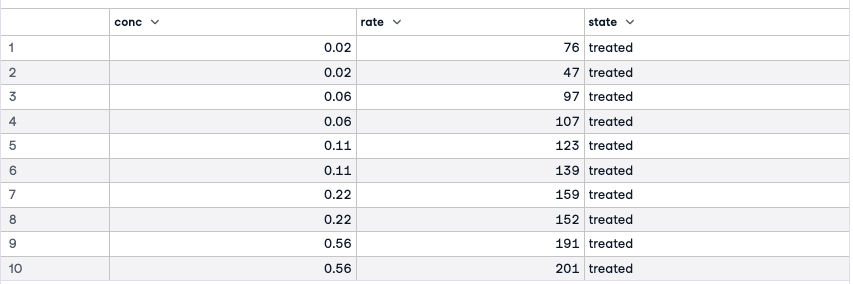

As três variáveis nesse quadro de dados são a concentração do substrato, a taxa inicial da reação e um indicador de tratado ou não tratado.

Ao traçar o gráfico da taxa em relação à concentração e rotular os dois níveis do tratamento, podemos ver um padrão geral. As curvas são assintóticas e bastante distintas para coortes de células tratadas e não tratadas.

plot(Puromycin$conc, Puromycin$rate, type="n", xlab = "conc", ylab = "rate")text(Puromycin$conc, Puromycin$rate,      ifelse(Puromycin$state == "treated", "T", "U"))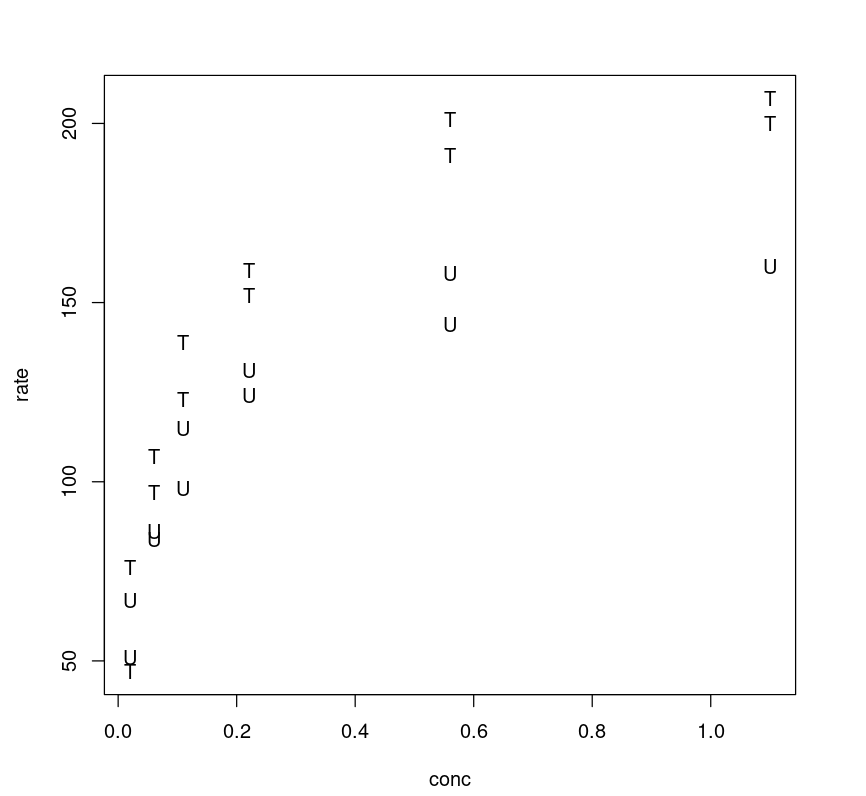

Como esses dados exibem uma forte relação de Michaelis-Menten entre a taxa de reação e a concentração, os pesquisadores esperam ajustar a seguinte equação matemática.

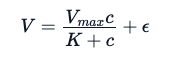
Aqui, o E é o erro de experimentação. Usando a mesma analogia usada para o modelo linear, por meio de um modelo especializado não linear, tentamos estimar os parâmetros Vmax e K que minimizarão a soma dos quadrados dos resíduos (no entanto, há outros métodos que podem ser usados para estimar esses parâmetros):

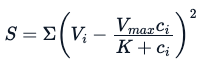
Ajuste de um modelo não linear

Apesar de conhecermos a relação, o ajuste de um modelo não linear não é tão simples, pois o modelo requer suposições iniciais para _Vmax e K . Se não for escolhido um bom palpite inicial, o modelo poderá se ajustar mal aos dados. Há duas opções para escolher:

• Observe o gráfico para encontrar os valores iniciais.
• Ou use uma função de autoinicialização (fornecida abaixo).

Para cada tipo de modelo, temos uma função de autoinicialização correspondente que pode ser usada para uma estimativa inicial.

Ajuste de um modelo usando uma estimativa inicial

Usando o valor inicial de Vmax = 160, K = 0,05 encontrado ao observar o gráfico, é possível usar a função R nls() para ajustar os dados. Normalmente, para a regressão linear, não é necessário especificar os parâmetros Vm ou K, mas isso é diferente para um modelo não linear. Todo algoritmo iterativo precisa de um bom ponto de partida. Caso contrário, ele pode não convergir. É assim que nos ajustamos a um modelo não linear em Puromycin com valores iniciais.

Purboth_1 <- nls(rate ~ (Vm)*conc/(K+conc), Puromycin, list(Vm=160, K=0.05))summary(Purboth_1)Formula: rate ~ (Vm) * conc/(K + conc)Parameters:Estimate Std. Error t value Pr(>|t|)Vm 190.80624 8.76459 21.770 6.84e-16 ***K 0.06039 0.01077 5.608 1.45e-05 ***---Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1Residual standard error: 18.61 on 21 degrees of freedomNumber of iterations to convergence: 5Achieved convergence tolerance: 5.121e-06

Calcular o erro residual

Calculamos o erro residual como:

sse <- Purboth_1$m$deviance()sse7276.54697931423

Calcule a variância explicada

Para encontrar a variância explicada por esse modelo (basicamente o R-quadrado na terminologia do modelo linear), precisamos encontrar a variância total na taxa ajustando um modelo nulo, estimando a média geral e extraindo as somas totais de quadrados, sst, do resumo do modelo nulo e, em seguida, usá-lo para calcular a porcentagem da variância explicada.

sse <- Purboth_1$m$deviance()null <- lm(rate~1, Puromycin)sst <- data.frame(summary.aov(null)[[1]])$Sum.Sqpercent_variation_explained = 100*(sst-sse)/sstpercent_variation_explained85.3488323994681

Esse modelo explica 85,34% das variações nos dados.

Ajuste usando o modelo com a função Self-Start

Como estamos usando o modelo Michaelis-Menten, é possível usar a função de autoinício SSmicmen(). No entanto, isso gera os mesmos resultados.

Purboth_self <- nls(rate~SSmicmen(conc,Vm,K), Puromycin)summary(Purboth_self)Formula: rate ~ SSmicmen(conc, Vm, K)Parameters:Estimate Std. Error t value Pr(>|t|)Vm 190.80667 8.76462 21.770 6.84e-16 ***K 0.06039 0.01077 5.608 1.45e-05 ***---Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1Residual standard error: 18.61 on 21 degrees of freedomNumber of iterations to convergence: 4Achieved convergence tolerance: 6.745e-06

Calcular o erro residual

sse <- Purboth_self$m$deviance()sse7276.54697947673

Calcular a variação explicada

É possível verificar a variância explicada pelo modelo.

sse <- Purboth_self$m$deviance()null <- lm(rate~1, Puromycin)sst <- data.frame(summary.aov(null)[[1]])$Sum.Sqpercent_variation_explained = 100*(sst-sse)/sstpercent_variation_explained85.348832399141

Em geral, a equação ajustada, que é a relação entre taxa e concentração, tem a seguinte aparência:

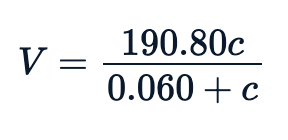
Visualizando o ajuste

É possível visualizar o desempenho do modelo traçando uma linha ajustada nos dados, que parece não linear.

plot(Puromycin$conc, Puromycin$rate, xlab="conc", ylab = "rate")lines(Puromycin[Puromycin$state == "treated",]$conc,       predict(Purboth_1, Puromycin[Puromycin$state == "treated",]), col=2)lines(Puromycin[Puromycin$state != "treated",]$conc,       predict(Purboth_1, Puromycin[Puromycin$state != "treated",]), col=2)

Melhor seleção de modelos

É possível ajustar ainda mais o modelo adicionando mais parâmetros. Se observarmos o gráfico entre a taxa e a concentração, poderemos notar que classes diferentes (tratadas e não tratadas) seguem trajetórias diferentes, e a diferença de taxa (eixo y) entre as trajetórias de duas classes pode ser aproximada como 40.

plot(Puromycin$conc, Puromycin$rate, type="n", xlab = "conc", ylab = "rate")text(Puromycin$conc, Puromycin$rate,      ifelse(Puromycin$state == "treated", "+", "*"))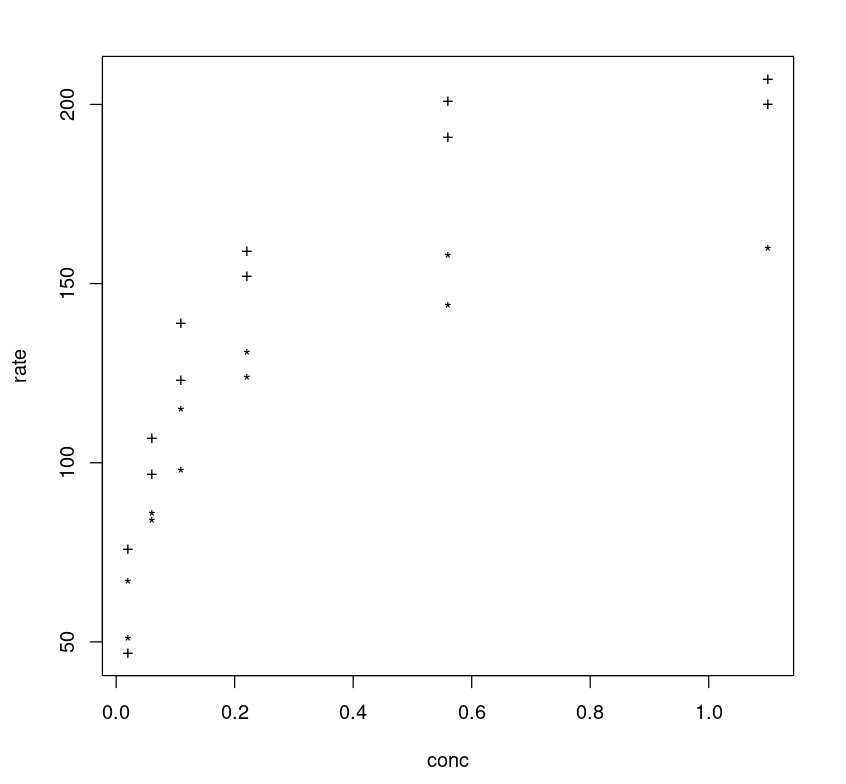

Essencialmente, estamos tentando ajustar um modelo condicionado à variável de estado, o que leva à seguinte equação não linear.

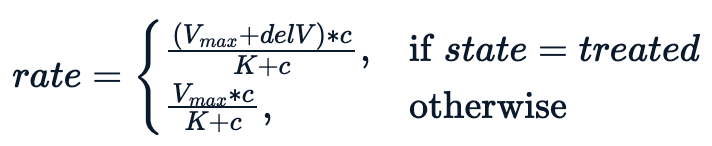
O modelo tem melhor desempenho com um parâmetro adicional delV. Atribuímos um valor inicial de 40 a delV e ajustamos o modelo usando nls com três parâmetros.

Purboth <- nls(rate ~ (Vm + delV*(state=="treated"))*conc/(K+conc), Puromycin,                list(Vm=160, delV=40, K=0.05))summary(Purboth)Formula: rate ~ (Vm + delV * (state == "treated")) * conc/(K + conc)Parameters:      Estimate Std. Error t value Pr(>|t|)    Vm   166.60397    5.80742  28.688  < 2e-16 ***delV  42.02591    6.27214   6.700 1.61e-06 ***K      0.05797    0.00591   9.809 4.37e-09 ***---Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1Residual standard error: 10.59 on 20 degrees of freedomNumber of iterations to convergence: 5 Achieved convergence tolerance: 8.93e-06

O resumo nos mostra que todos os três parâmetros são estatisticamente significativos.

Calcular o erro residual

É possível observar que, para esse modelo, o erro residual é substancialmente reduzido:

sse <- Purboth$m$deviance()sse2240.89143883885

Calcular a variação explicada

Há mais variação explicada por esse modelo.

sse <- Purboth$m$deviance()null <- lm(rate~1, Puromycin)sst <- data.frame(summary.aov(null)[[1]])$Sum.Sqpercent_variation_explained = 100*(sst-sse)/sstpercent_variation_explained95.4880142822744

Verificação da AIC

Também é possível executar a verificação AIC em ambos os modelos, embora atualmente a prática comum seja usar a validação cruzada; no entanto, isso requer mais dados; em geral, quanto menor o AIC, melhor é o modelo.

AIC(Purboth)AIC(Purboth_1)178.591273238391203.680274951742

Visualizando o ajuste

É possível visualizar o desempenho do modelo ajustado traçando uma linha ajustada nos dados. Não é de surpreender que o modelo ajustado nos proporcione um ajuste melhor para diferentes classes.

plot(Puromycin$conc, Puromycin$rate, xlab="conc", ylab = "rate")lines(Puromycin[Puromycin$state == "treated",]$conc, predict(Purboth, Puromycin[Puromycin$state == "treated",]), col=2)lines(Puromycin[Puromycin$state != "treated",]$conc, predict(Purboth, Puromycin[Puromycin$state != "treated",]), col=3)legend(0, 200, legend = c("treated", "untreated"), fill = c(2,3))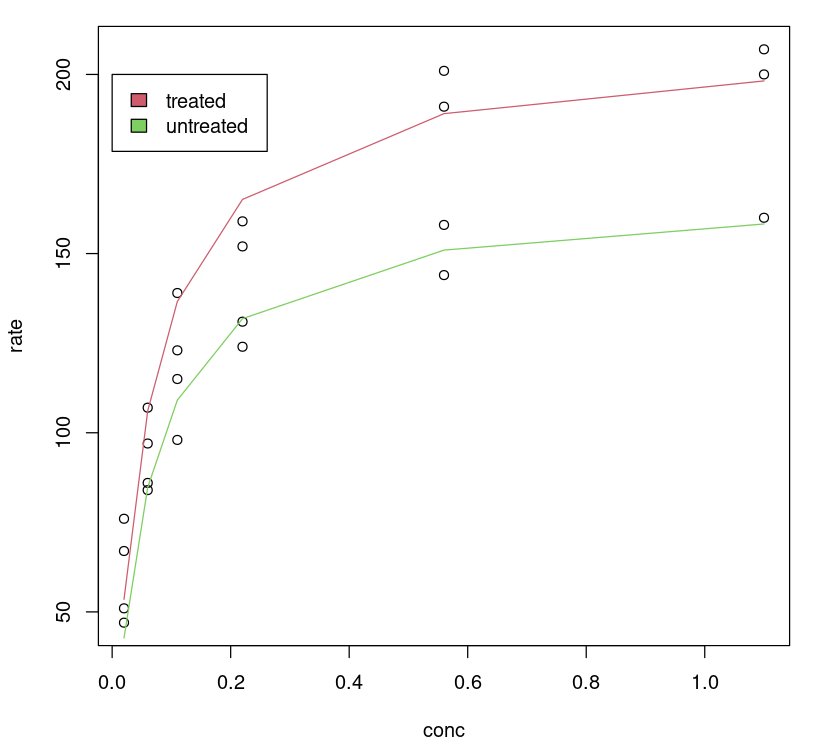

Intervalo de confiança dos parâmetros

Não se pode confiar nos valores de p. O intervalo de confiança de 95% fornece os valores do coeficiente para cada parâmetro significativo em 2,5% e 97,5%. Nenhum deles inclui 0.

confint(Purboth)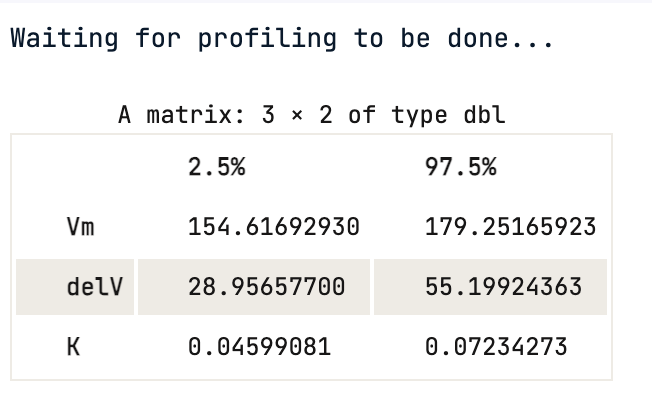

Usando o valor do intervalo de confiança, pode-se dizer estatisticamente que há uma chance de 95% de que um valor verdadeiro do parâmetro, por exemplo, Vmax, esteja dentro do intervalo fornecido acima, que é (154,62, 179,25) para Vmax.

Criação de perfil

É possível traçar um perfil adicional do modelo para entender a incerteza na estimativa de parâmetros examinando diretamente a função objetiva. Em nosso modelo, temos três parâmetros, Vmax, delV e K, e podemos traçar o perfil deles:

• Para obter o intervalo de confiança.
• E use a função de perfil t, que é semelhante à estatística t usada pelo modelo linear. Os gráficos da função t de perfil fornecem os intervalos de probabilidade para parâmetros individuais e explicam como a estimativa não é linear.

Representação gráfica do intervalo de confiança

Isso representa o intervalo de confiança dos parâmetros para diferentes valores de (que corresponde a diferentes intervalos de confiança (99%, 95%, 90%, 80% e 50%). É semelhante ao intervalo de confiança (95%) fornecido por confint(object, parm, level = 0.95, ...)function.

Purbothpf = profile(Purboth)par( mfrow= c(2,2) )plot(Purbothpf)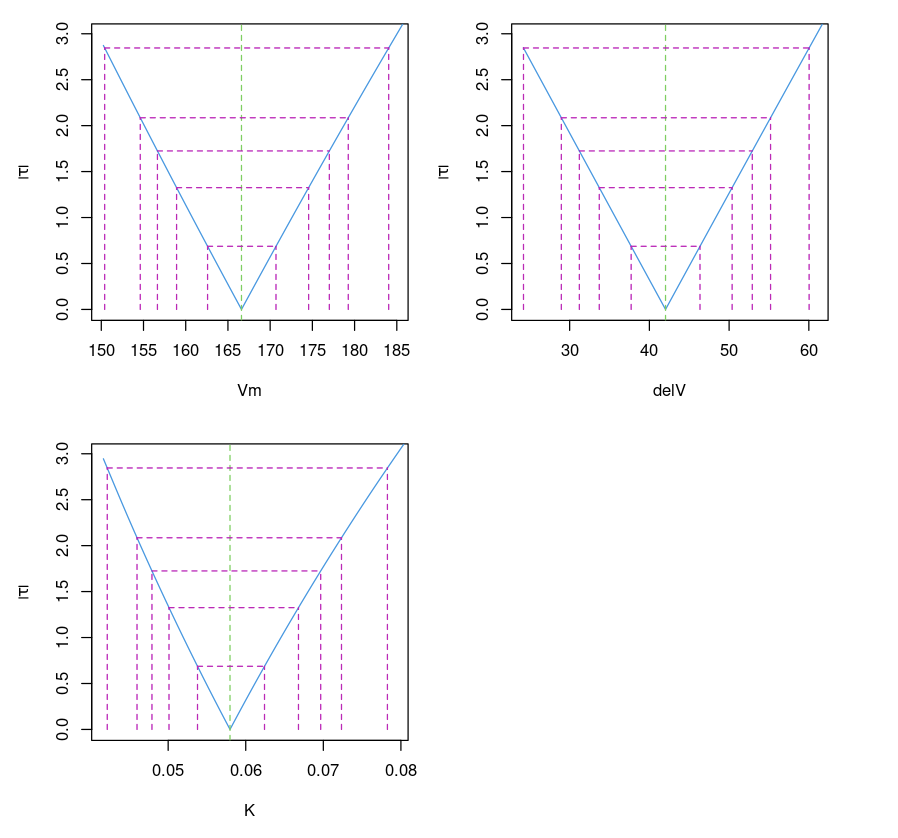

Plotagem _T versus parâmetros

O gráfico de três parâmetros Vmax, delV, K vs _T nos dá uma ideia se o ajuste é linear ou não linear. É possível observar que a linha parece linear para os parâmetros delV e Vm, e ligeiramente curva para K. Isso é esperado porque o parâmetro K apresenta uma relação não linear.

dataVm = data.frame(Purbothpf$Vm$par.vals)datadelV = data.frame(Purbothpf$delV$par.vals)dataK = data.frame(Purbothpf$K$par.vals)par( mfrow= c(2,2) )plot(dataVm$Vm,Purbothpf$Vm$tau, type="l", xlab = "Vm", ylab = "Tau")plot(datadelV$delV,Purbothpf$delV$tau, type="l", xlab = "delV", ylab = "Tau")plot(dataK$K,Purbothpf$K$tau, type="l", xlab = "K", ylab = "Tau")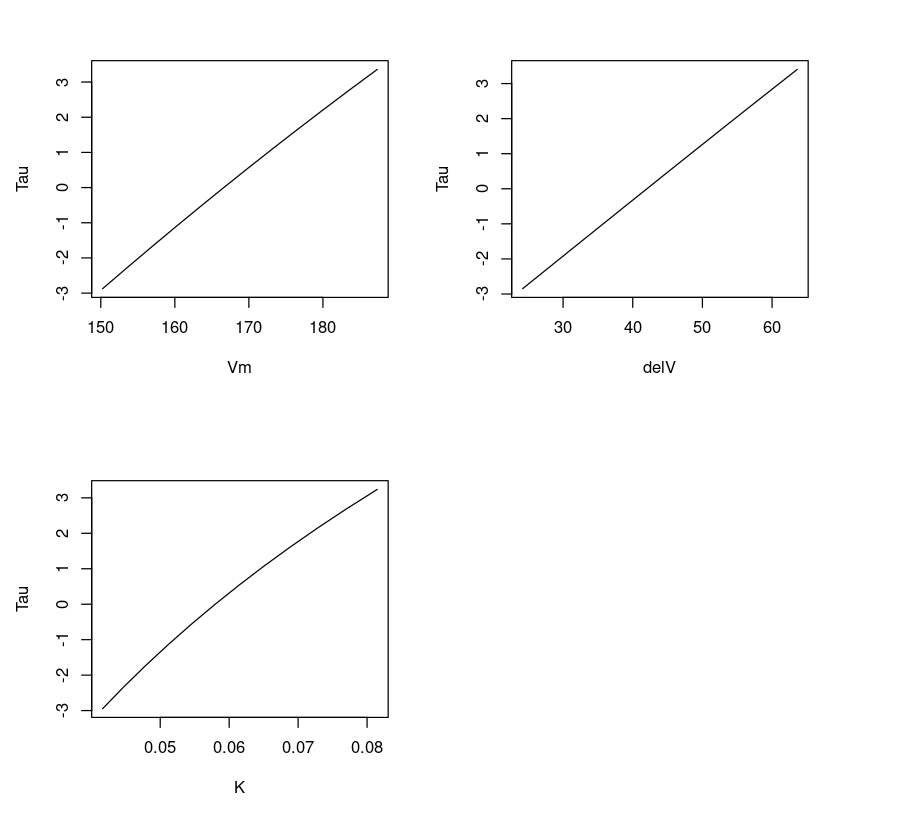

Ajuste de um modelo linear

É possível usar a mesma função da biblioteca R nls() para ajustar em um modelo linear, conforme mostrado abaixo. Acho que é um bom hábito sempre tentar um modelo linear para fins de interpretação e comparação.

PurbothRealLinear <- nls(rate ~ i + m*conc, Puromycin, list(i=160, m=0.05) )summary(PurbothRealLinear)Formula: rate ~ i + m * concParameters:  Estimate Std. Error t value Pr(>|t|)    i    93.92       8.00   11.74 1.09e-10 ***m   105.40      16.92    6.23 3.53e-06 ***---Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1Residual standard error: 28.82 on 21 degrees of freedomNumber of iterations to convergence: 2 Achieved convergence tolerance: 2.571e-09

Embora os parâmetros pareçam significativos, o ajuste é ruim. O erro padrão residual é alto.

Visualizando o ajuste

Parece que o modelo linear tem um desempenho ruim; é possível visualizar isso traçando uma linha ajustada nos dados e comparando-a com sua contraparte não linear.

plot(Puromycin$conc, Puromycin$rate, xlab="conc", ylab = "rate")lines(Puromycin$conc, predict(PurbothRealLinear), col=4)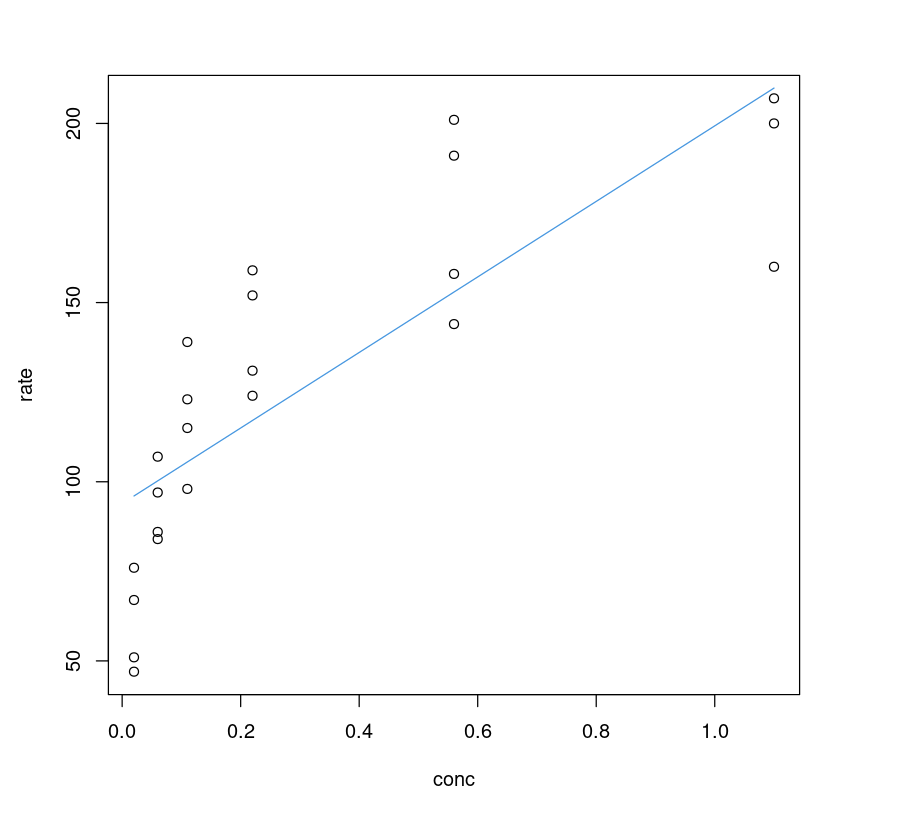

Comparação analítica entre modelos não lineares e lineares

Com base no gráfico acima, sabemos que o modelo linear faz um trabalho ruim, mas como podemos comparar esses modelos? Será como comparar maçãs com laranjas. AIC resultados não podem ser usados diretamente.

Adequação

O que constitui um bom ajuste - para regressão, é o valor previsto e o valor real serem os mais próximos possíveis. Portanto, se inspecionarmos a qualidade do que um modelo previu usando a função lm() do R, poderemos compará-los. O modelo mais preciso fará com que os pontos fiquem próximos da linha ideal. Uma linha ideal é um modelo 100% preciso - o valor previsto é o mesmo que o valor real para cada ponto de dados. Portanto, todos os pontos estarão em uma linha reta.

Ajuste não linear

Portanto, para cada ponto de dados de entrada, usamos o modelo para prever o valor-alvo e, em seguida, aplicamos a função lm(), conforme mostrado. Ao traçar um gráfico de dispersão entre a taxa real (eixo x) e a taxa prevista (eixo y) e desenhar uma linha ideal, é possível observar a proximidade dos pontos em relação à linha.

nonLinear_df = data.frame("rate"=Puromycin$rate, "pred_rate"= predict(Purboth))fit_nonLinear = lm(nonLinear_df$rate ~ nonLinear_df$pred_rate)AIC(fit_nonLinear)plot(nonLinear_df$rate, nonLinear_df$pred_rate, xlab="actual_rate",      ylab = "pred_rate",      main = "Comparing Actual vs Predicted for Non Linear Model")lines(Puromycin$rate, Puromycin$rate)174.711198508104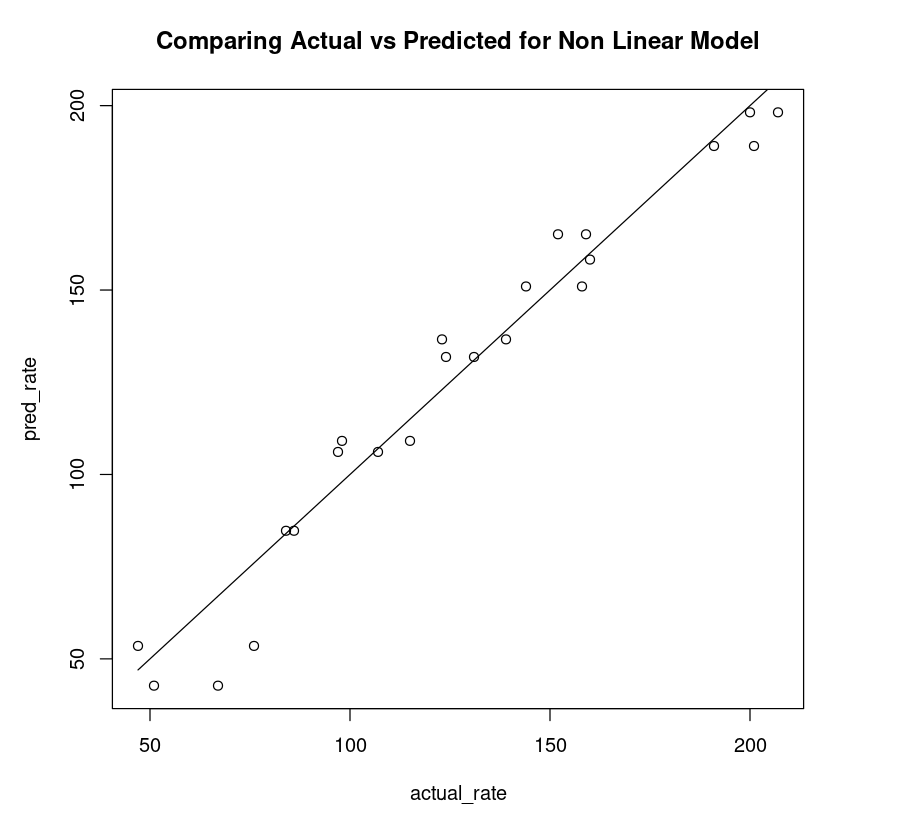

Ajuste linear

O gráfico não linear acima é claramente um ajuste melhor em comparação com o gráfico linear (abaixo).

linear_df = data.frame("rate"=Puromycin$rate, "pred_rate"= predict(PurbothRealLinear))fit_linear = lm(linear_df$rate~linear_df$pred_rate)AIC(fit_linear)plot(linear_df$rate, linear_df$pred_rate, xlab="actual_rate", ylab = "pred_rate",      main= "Comparing Actual vs Predicted using lm()")lines(Puromycin$rate, Puromycin$rate)223.783416979551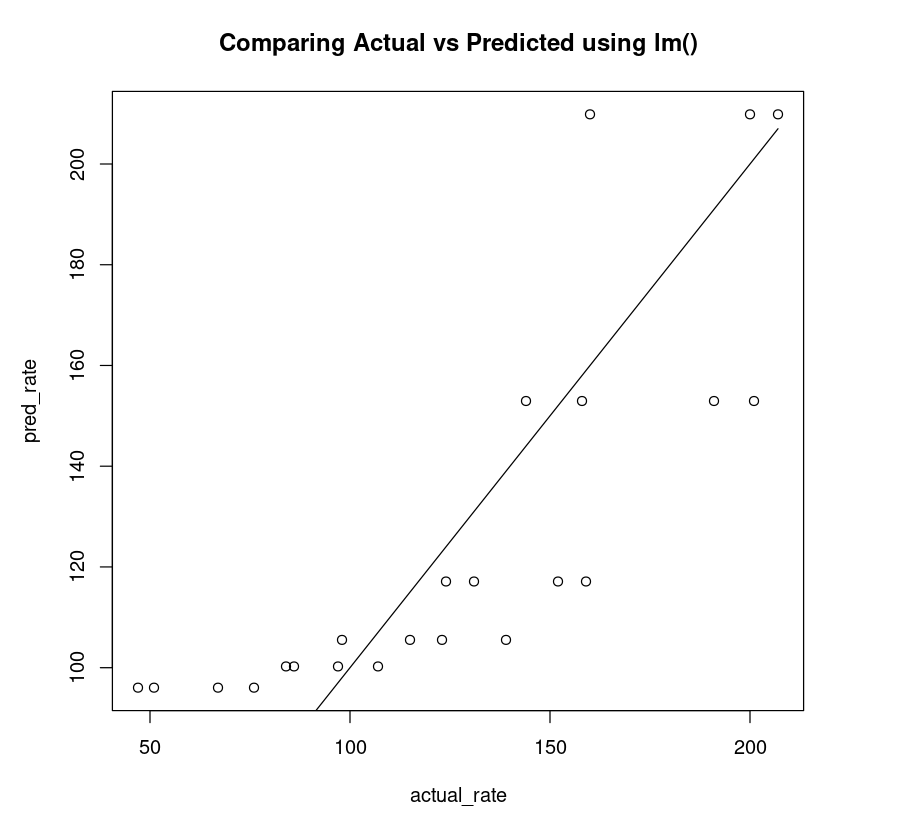

Aprimoramento do modelo linear

Parece que estamos sendo injustos com o modelo linear porque vemos claramente que os dados não seguem uma linha reta, então podemos tentar ajustar o modelo usando dados transformados. Escolhemos sqrt() para transformar a conc e ajustamos um modelo linear, conforme mostrado abaixo.

PurbothLinearSqrt = nls(rate ~ i + m*sqrt(conc), Puromycin, list(i=160, m=0.05) )summary(PurbothLinearSqrt)Formula: rate ~ i + m * sqrt(conc)Parameters:  Estimate Std. Error t value Pr(>|t|)    i   60.961      8.758   6.961 7.11e-07 ***m  139.134     15.675   8.876 1.50e-08 ***---Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1Residual standard error: 22.31 on 21 degrees of freedomNumber of iterations to convergence: 2 Achieved convergence tolerance: 1.838e-09

De fato, há uma queda no erro padrão residual, mas ela é menor do que a esperada.

Plotagem do ajuste

É possível ver que o uso de sqrt() em conc melhora o modelo linear. Entretanto, em comparação com o modelo não linear Purboth, ele não é melhor. O erro padrão residual do modelo PurbothLinearSqrt é quase o dobro do modelo Purboth, portanto, não analisaremos mais esse modelo. É possível tentar ajustar termos polinomiais de ordem superior (usando regressão polinomial), mas o esforço necessário para ajustar esse modelo é muito maior quando é possível obter melhores resultados usando um modelo não linear.

plot(Puromycin$conc, Puromycin$rate, xlab="conc", ylab = "rate")lines(Puromycin[Puromycin$state != "treated",]$conc, predict(PurbothLinearSqrt, Puromycin[Puromycin$state != "treated",]), col=2)lines(Puromycin[Puromycin$state != "treated",]$conc, predict(PurbothLinearSqrt, Puromycin[Puromycin$state != "treated",]), col=3)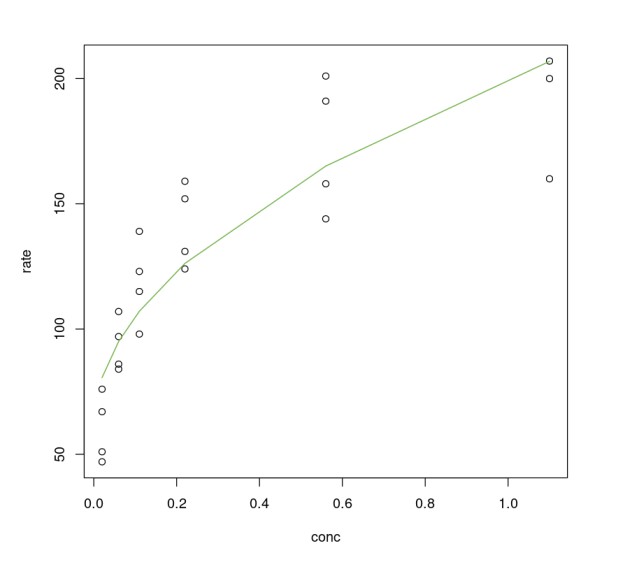

Desenrolando a equação de não linearidade

É possível aplicar um truque para desvendar uma função não linear e ajustar um modelo linear. Essa técnica era usada no passado, quando os cálculos eram feitos à mão, e não por computadores. No entanto, esses modelos não conseguem fazer um trabalho melhor.

Conversão da forma não linear em linear

Como ilustração, é possível alterar a equação de Michaelis-Menten tomando seu inverso, conforme mostrado abaixo, e usar a forma modificada para aplicar um modelo linear.

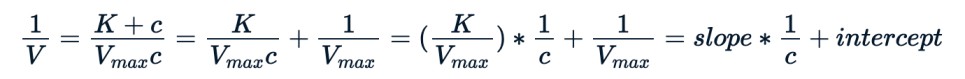
Podemos usar o mesmo nls() para ajustar a nova equação.

PurbothPseudoLinear <- nls((1/rate) ~ K /(Vm*conc) + 1/Vm , Puromycin,                            list(Vm=160, K=0.05))summary(PurbothPseudoLinear)Formula: (1/rate) ~ K/(Vm * conc) + 1/VmParameters:    Estimate Std. Error t value Pr(>|t|)    Vm 1.674e+02  1.362e+01  12.287 4.70e-11 ***K  3.900e-02  6.172e-03   6.318 2.89e-06 ***---Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1Residual standard error: 0.001786 on 21 degrees of freedomNumber of iterations to convergence: 3 Achieved convergence tolerance: 2.997e-09

O erro padrão residual é baixo, mas os dados usados, portanto, não podem ser usados para comparação com modelos não lineares. Nossa melhor aposta é visualizar o desempenho de ambos os modelos no conjunto de dados original.

Plotagem do ajuste

Comparamos o modelo Purboth_1, que usa dois parâmetros Vmax, K com o PurbothPseudoLinear. O gráfico mostra claramente que um modelo não linear faz um trabalho melhor.

plot(Puromycin$conc, Puromycin$rate, xlab="conc", ylab = "rate",      main = "Scatterplot conc vs rate")lines(Puromycin[Puromycin$state == "treated",]$conc,       predict(Purboth_1, Puromycin[Puromycin$state == "treated",]), col=2)lines(Puromycin[Puromycin$state != "treated",]$conc,       predict(Purboth_1, Puromycin[Puromycin$state != "treated",]), col=2)lines(Puromycin[Puromycin$state == "treated",]$conc,       1/predict(PurbothPseudoLinear, Puromycin[Puromycin$state == "treated",])      , col=4)lines(Puromycin[Puromycin$state != "treated",]$conc,       1/predict(PurbothPseudoLinear, Puromycin[Puromycin$state != "treated",])      , col=4)legend(0, 200, legend = c("nls", "nls-turned-linear"), fill = c(2,4))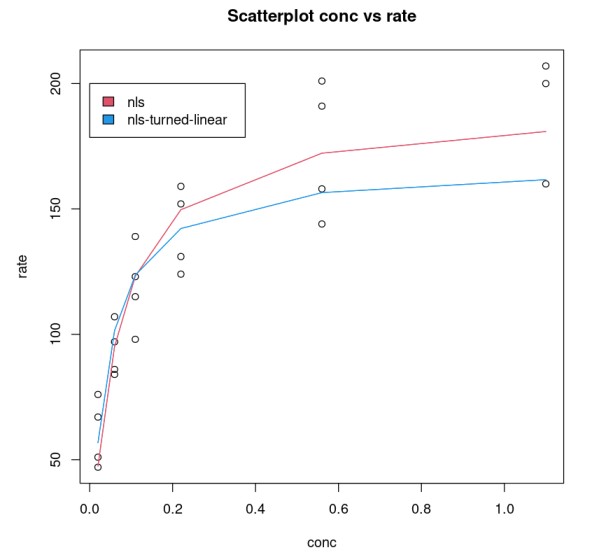

Adequação

É possível comparar a qualidade do modelo.

nonLinear_df = data.frame("rate"=Puromycin$rate, "pred_rate"= predict(Purboth_1))fit_nonLinear = lm(nonLinear_df$rate ~ nonLinear_df$pred_rate)AIC(fit_nonLinear)203.017860461858

linear_df = data.frame("rate"=Puromycin$rate,                        "pred_rate"= 1/predict(PurbothPseudoLinear))fit_linear = lm(linear_df$rate~linear_df$pred_rate)AIC(fit_linear)206.999538212925

Isso mostra que um modelo que usa uma função não linear tem um desempenho muito melhor.

par( mfrow= c(1,2) )plot(nonLinear_df$rate, nonLinear_df$pred_rate, xlab="actual_rate",      ylab = "pred_rate",      main = "Non-Linear")lines(Puromycin$rate, Puromycin$rate)plot(linear_df$rate, linear_df$pred_rate, xlab="actual_rate", ylab = "pred_rate",      main = "Turned Linear")lines(Puromycin$rate, Puromycin$rate)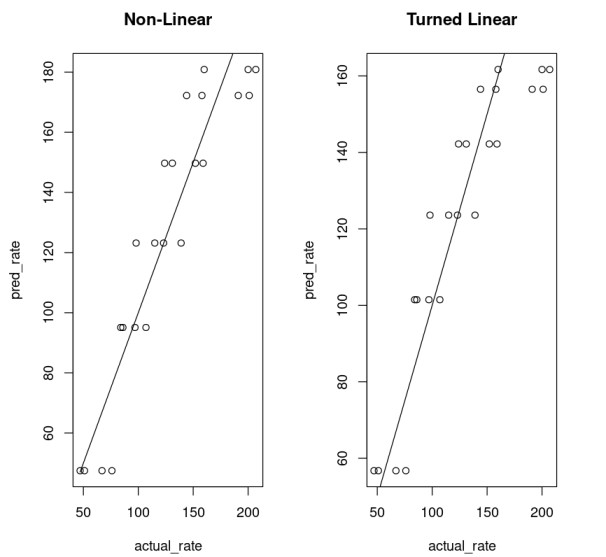

Conclusão

O modelo não linear tem um desempenho melhor do que o equivalente linear, especialmente nos casos em que temos dados mecanísticos. No entanto, um modelo não linear não garante uma solução numérica para um problema de estimativa. É possível traçar e selecionar uma função matemática que possa explicar melhor a relação entre os dados. Nesses casos, o modelo não linear pode substituir sua contraparte linear.

Se você achou este artigo esclarecedor e deseja se aprofundar no mundo dos modelos de regressão, confira o curso Intermediate Regression in R (Regressão intermediária em R ) do DataCamp.