Curso
Imagine-se navegando em um labirinto. A cada passo, você enfrenta uma decisão que o leva para mais perto da saída ou para mais fundo no labirinto. Isso é semelhante a um algoritmo de árvore de decisão, um método poderoso e intuitivo de aprendizado de máquina que nos ajuda a entender dados complexos e a escolher o melhor curso de ação.
Um algoritmo de árvore de decisão divide um conjunto de dados em subconjuntos cada vez menores com base em determinadas condições. Como uma árvore de ramificação com folhas e nós, ela começa com um único nó raiz e se expande em várias ramificações, cada uma representando uma decisão com base no valor de um recurso. As folhas finais da árvore são os possíveis resultados ou previsões.
Este artigo apresentará a você o mundo das árvores de decisão usando a linguagem de programação R. Discutiremos os conceitos básicos, analisaremos os tipos populares de algoritmos de árvore de decisão, exploraremos os métodos baseados em árvore e o orientaremos em um exemplo passo a passo. Ao final, você poderá aproveitar o poder das árvores de decisão para tomar melhores decisões baseadas em dados.
O que é uma árvore de decisão em aprendizado de máquina?
As árvores de decisão são especiais no aprendizado de máquina devido à sua simplicidade, interpretabilidade e versatilidade.
É um algoritmo de aprendizado de máquina supervisionado que pode ser usado tanto para problemas de regressão (previsão de valores contínuos) quanto de classificação (previsão de valores categóricos). Além disso, elas servem como base para técnicas mais avançadas, como bagging, boosting e florestas aleatórias.
O diagrama abaixo ilustrará as terminologias por trás das árvores de decisão:
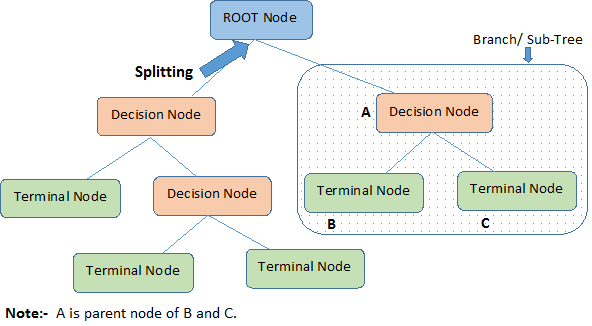
Uma árvore de decisão começa com um nó raiz que significa toda a população ou amostra, que então se separa em dois ou mais grupos uniformes por meio de um método chamado divisão. Quando os subnós passam por mais divisões, eles são identificados como nós de decisão, enquanto os que não se dividem são chamados de nós terminais ou folhas. Um segmento de uma árvore completa é chamado de ramo.
Estabelecemos que as árvores de decisão podem ser usadas tanto para tarefas de regressão quanto de classificação; portanto, vamos entender o algoritmo por trás dos tipos de árvores de decisão.
Tipos populares de algoritmos de árvores de decisão
Vamos entender intuitivamente as árvores de decisão de regressão e classificação, o que é semelhante e diferente em cada uma delas e as funções de erro.
Árvores de regressão
Vamos dar uma olhada na imagem abaixo, que ajuda a visualizar a natureza do particionamento realizado por uma árvore de regressão. Isso mostra uma árvore não podada e uma árvore de regressão ajustada a um conjunto de dados aleatórios. Ambas as visualizações mostram uma série de regras de divisão, começando no topo da árvore. Observe que cada divisão do domínio está alinhada com um dos eixos de recursos. O conceito de divisão paralela de eixos se generaliza diretamente para dimensões maiores que dois. Para um espaço de recursos de tamanho $p$, um subconjunto de $\mathbb{R}^p$, o espaço é dividido em $M$ regiões, $R_{m}$, cada uma das quais é um "hiperbloco" de dimensão $p$.
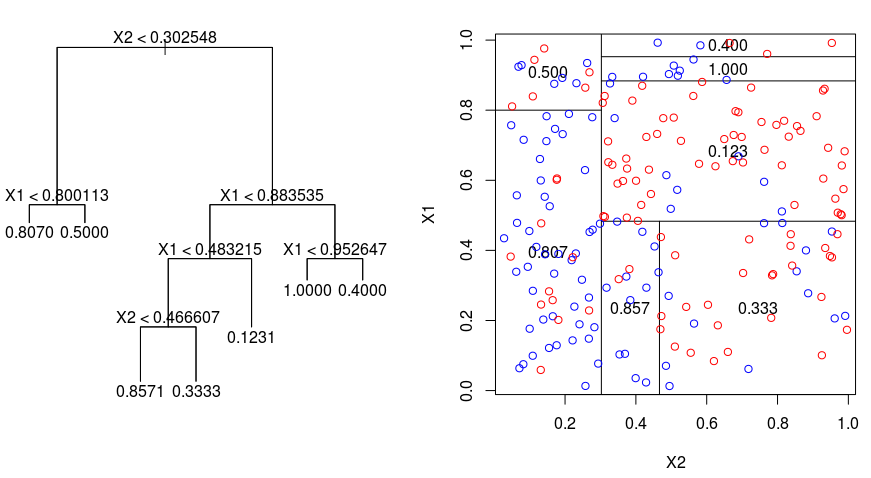
Para criar uma árvore de regressão, primeiro você usa a divisão binária recursiva para desenvolver uma árvore grande nos dados de treinamento, parando somente quando cada nó terminal tiver menos do que um número mínimo de observações. A divisão binária recursiva é um algoritmo guloso e de cima para baixo usado para minimizar a soma residual de quadrados (RSS), uma medida de erro também usada em configurações de regressão linear. O RSS, no caso de um espaço de recursos particionado com M partições, é dado por:
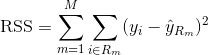
Começando no topo da árvore, você a divide em dois galhos, criando uma partição de dois espaços. Em seguida, você executa essa divisão específica no topo da árvore várias vezes e escolhe a divisão dos recursos que minimiza o RSS (atual).
Em seguida, você aplica a poda de complexidade de custo à árvore grande para obter uma sequência das melhores subárvores, como uma função de $\alpha$. A ideia básica aqui é introduzir um parâmetro de ajuste adicional, denotado por $\alpha$, que equilibra a profundidade da árvore e sua adequação aos dados de treinamento.
Você pode usar a validação cruzada K-fold para escolher $\alpha$. Essa técnica envolve simplesmente a divisão das observações de treinamento em K dobras para estimar a taxa de erro de teste das subárvores. Seu objetivo é selecionar aquele que leva à menor taxa de erro.
Árvores de classificação
Uma árvore de classificação é muito semelhante a uma árvore de regressão, exceto pelo fato de ser usada para prever uma resposta qualitativa em vez de uma quantitativa.
Lembre-se de que, em uma árvore de regressão, a resposta prevista para uma observação é dada pela resposta média das observações de treinamento que pertencem ao mesmo nó terminal. Por outro lado, em uma árvore de classificação, você prevê que cada observação pertence à classe de observações de treinamento que ocorre com mais frequência na região à qual ela pertence.
Ao interpretar os resultados de uma árvore de classificação, muitas vezes você está interessado não apenas na previsão de classe correspondente a uma determinada região do nó terminal, mas também nas proporções de classe entre as observações de treinamento que se enquadram nessa região.
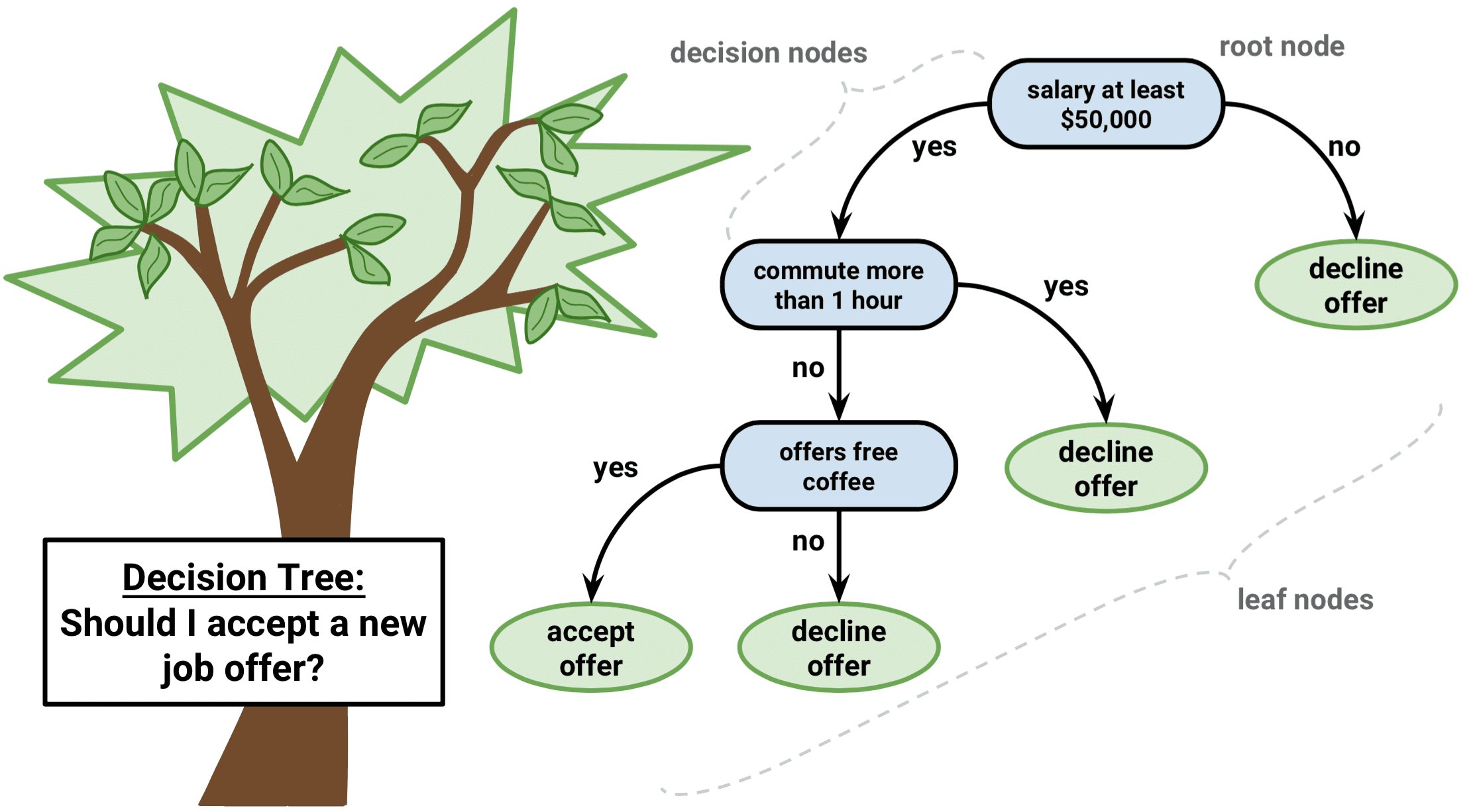
A tarefa de desenvolver uma árvore de classificação é bastante semelhante à tarefa de desenvolver uma árvore de regressão. Assim como na configuração de regressão, você usa a divisão binária recursiva para desenvolver uma árvore de classificação. No entanto, na configuração de classificação, a soma residual de quadrados não pode ser usada como critério para fazer as divisões binárias. Em vez disso, você pode usar um dos três métodos abaixo:
- Taxa de erro de classificação: Em vez de ver a distância de uma resposta numérica em relação ao valor médio, como na configuração de regressão, você pode definir a "taxa de acerto" como a fração de observações de treinamento em uma determinada região que não pertence à classe de ocorrência mais ampla. O erro é dado por esta equação:
E = 1 - argmaxc($\hat{\pi}_{mc}$)
em que $\hat{\pi}_{mc}$ representa a fração dos dados de treinamento na região Rm que pertencem à classe c.
- Índice de Gini: O Índice de Gini é uma métrica de erro alternativa projetada para mostrar o grau de "pureza" de uma região. "Pureza", nesse caso, significa quanto dos dados de treinamento em uma determinada região pertence a uma única classe. Se uma região Rm contiver dados que sejam principalmente de uma única classe c, o valor do Índice de Gini será pequeno:
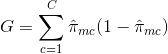
- Etropia cruzada: Uma terceira alternativa, que é semelhante ao Índice de Gini, é conhecida como entropia cruzada ou desvio:
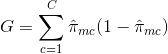
A entropia cruzada assumirá um valor próximo de zero se os $\hat{\pi}_{mc}$ estiverem todos próximos de 0 ou de 1. Portanto, assim como o índice Gini, a entropia cruzada assumirá um valor pequeno se o nó m for puro. De fato, verifica-se que o índice de Gini e a entropia cruzada são bastante semelhantes numericamente.
Ao criar uma árvore de classificação, o índice Gini ou a entropia cruzada são normalmente usados para avaliar a qualidade de uma divisão específica, pois são mais sensíveis à pureza do nó do que a taxa de erro de classificação. Qualquer uma dessas três abordagens pode ser usada ao podar a árvore, mas a taxa de erro de classificação é preferível se o objetivo for a precisão da previsão da árvore podada final.
Vantagens e desvantagens das árvores de decisão
Por mais que queiramos entender o algoritmo e seus pontos fortes, é fundamental entender suas deficiências. A verdade é que as árvores de decisão não são a melhor opção para todos os tipos de algoritmos de aprendizado de máquina, o que também é o caso de todos os algoritmos de aprendizado de máquina.
Aqui estão as vantagens e desvantagens:
Vantagens
- Fácil de entender e interpretar. As árvores de decisão são altamente intuitivas e podem ser facilmente visualizadas. Sua estrutura hierárquica assemelha-se à tomada de decisão humana, tornando-a acessível até mesmo para não especialistas. Essa capacidade de interpretação é crucial em situações em que a compreensão do processo de decisão é tão importante quanto a própria previsão.
- Pode lidar com variáveis contínuas e categóricas. As árvores de decisão são versáteis e podem gerenciar conjuntos de dados com uma combinação de recursos contínuos e categóricos, bem como variáveis-alvo de ambos os tipos. Essa flexibilidade permite que as árvores de decisão sejam aplicadas a uma ampla gama de problemas.
- É necessário um mínimo de pré-processamento de dados. As árvores de decisão não exigem escalonamento ou normalização de recursos, pois são invariáveis a transformações monotônicas. Eles também podem lidar facilmente com valores ausentes e outliers, o que os torna adequados para dados brutos e ruidosos.
- Pode ser usado para seleção de recursos e identificação de variáveis importantes. As árvores de decisão realizam naturalmente a seleção de recursos, escolhendo os recursos mais informativos para dividir os dados. A importância de um recurso pode ser determinada com base na antecedência com que ele aparece na árvore e na frequência com que é usado para divisão.
Disadvantages
- Propenso ao ajuste excessivo. As árvores de decisão podem se tornar excessivamente complexas quando se tornam profundas, levando a um ajuste excessivo dos dados de treinamento. Isso resulta em uma generalização ruim de dados não vistos. Técnicas como a poda ou a definição de uma profundidade máxima podem ajudar a reduzir esse problema.
- Sensível a pequenas alterações nos dados. Uma pequena alteração nos dados de treinamento pode levar a uma estrutura de árvore completamente diferente, tornando as árvores de decisão instáveis. Essa sensibilidade pode ser reduzida por métodos de conjunto, como bagging, boosting ou florestas aleatórias, que criam várias árvores e agregam seus resultados.
- Os modelos de árvore de decisão geralmente não são tão precisos quanto outros métodos de aprendizado de máquina. Devido à sua simplicidade e à natureza gananciosa de sua construção, as árvores de decisão nem sempre produzem os modelos mais precisos. No entanto, eles podem servir como um bom ponto de partida ou modelo de linha de base para comparação com métodos mais sofisticados.
- Preconceito em relação às classes dominantes. As árvores de decisão podem ser tendenciosas em relação à classe majoritária em conjuntos de dados desequilibrados, levando a divisões abaixo do ideal e à classificação incorreta de instâncias minoritárias. Técnicas como sobreamostragem, subamostragem ou uso de aprendizado sensível ao custo podem ajudar a resolver esse problema.
Apesar dessas desvantagens, as árvores de decisão continuam sendo uma escolha popular em muitas aplicações devido à sua simplicidade, interpretabilidade e versatilidade.
Algoritmos avançados de aprendizado de máquina com base em árvores
Vamos explorar os métodos de conjunto baseados em árvores que aproveitam os pontos fortes das árvores de decisão e abordam algumas de suas limitações: bagging, boosting e florestas aleatórias.
Ensacamento
As árvores de decisão discutidas acima sofrem de alta variância, o que significa que, se você dividir os dados de treinamento em duas partes aleatoriamente e ajustar uma árvore de decisão às duas metades, os resultados obtidos poderão ser bem diferentes. Por outro lado, um procedimento com baixa variação produzirá resultados semelhantes se aplicado repetidamente a conjuntos de dados distintos.
Bagging, ou agregação bootstrap, é uma técnica usada para reduzir a variação de suas previsões, combinando o resultado de vários classificadores modelados em diferentes subamostras do mesmo conjunto de dados. Aqui está a equação para ensacamento:
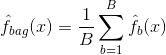
no qual você gera $B$ conjuntos de dados de treinamento bootstrapped diferentes. Em seguida, você treina seu método no conjunto de treinamento bootstrapped $bth$ para obter $\hat{f}_{b}(x)$ e, por fim, calcula a média das previsões.
A imagem abaixo mostra as três etapas diferentes do ensacamento:
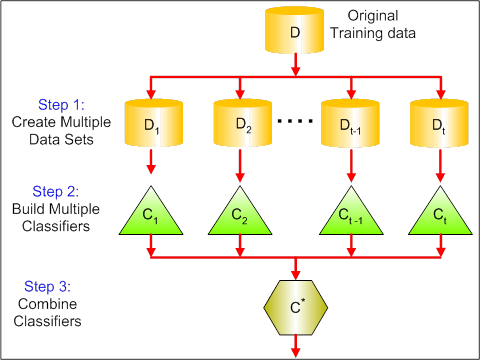
-
Etapa 1: Aqui você substitui os dados originais por novos dados. Os novos dados geralmente têm uma fração das colunas e linhas dos dados originais, que podem ser usados como hiperparâmetros no modelo de ensacamento.
-
Etapa 2: Você cria classificadores em cada conjunto de dados. Em geral, você pode usar o mesmo classificador para criar modelos e previsões.
-
Etapa 3: Por fim, você usa um valor médio para combinar as previsões de todos os classificadores, dependendo do problema. Em geral, esses valores combinados são mais robustos do que um único modelo.
Embora o ensacamento possa melhorar as previsões de muitos métodos de regressão e classificação, ele é particularmente útil para árvores de decisão. Para aplicar o bagging a árvores de regressão/classificação, basta construir $B$ árvores de regressão/classificação usando $B$ conjuntos de treinamento bootstrapped e calcular a média das previsões resultantes. Essas árvores crescem profundamente e não são podadas. Portanto, cada árvore individual tem alta variação, mas baixa tendência. O cálculo da média dessas árvores $B$ reduz a variação.
Em termos gerais, foi demonstrado que o bagging proporciona melhorias impressionantes na precisão ao combinar centenas ou até milhares de árvores em um único procedimento.
Florestas aleatórias
O Random Forests é um método versátil de aprendizado de máquina capaz de realizar tarefas de regressão e classificação. Ele também utiliza métodos de redução dimensional, trata valores ausentes, valores discrepantes e outras etapas essenciais da exploração de dados, e faz um trabalho bastante bom.
O Random Forests melhora as árvores ensacadas por meio de um pequeno ajuste que descorrelaciona as árvores. Como no bagging, você cria várias árvores de decisão em amostras de treinamento com bootstrapping. Porém, ao criar essas árvores de decisão, cada vez que uma divisão em uma árvore é considerada, uma amostra aleatória de m preditores é escolhida como candidata à divisão do conjunto completo de $p$ preditores. A divisão pode usar apenas um desses $m$ preditores. Essa é a principal diferença entre as florestas aleatórias e o ensacamento, pois, como no ensacamento, a escolha do preditor $m = p$.
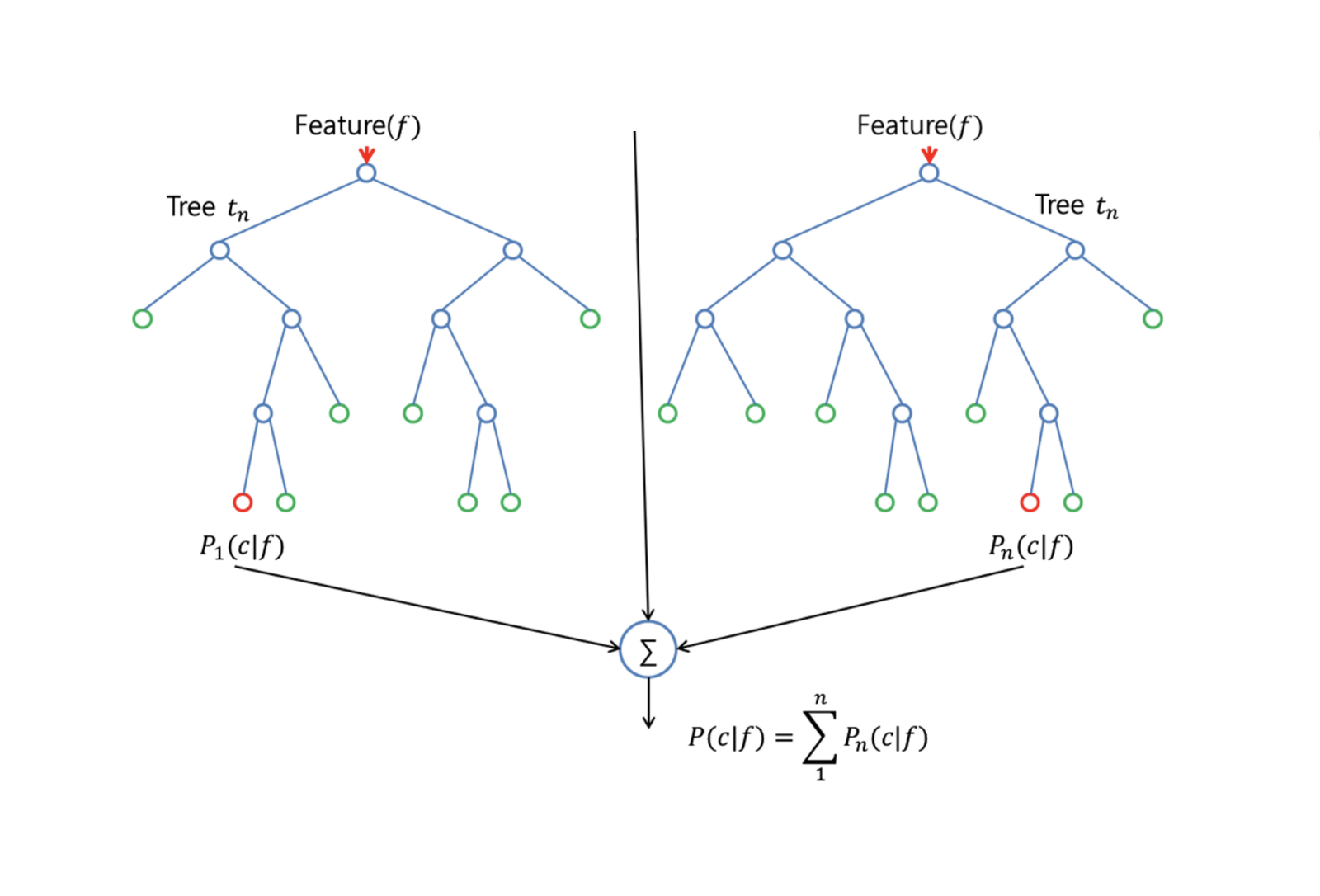
Para desenvolver uma floresta aleatória, você deve:
-
Primeiro, suponha que o número de casos no conjunto de treinamento seja K. Em seguida, pegue uma amostra aleatória desses K casos e use essa amostra como o conjunto de treinamento para o crescimento da árvore.
-
Se houver $p$ variáveis de entrada, especifique um número $m < p$ de modo que, em cada nó, você possa selecionar $m$ variáveis aleatórias dentre as $p$. A melhor divisão desses $m$ é usada para dividir o nó.
-
Posteriormente, cada árvore é cultivada na maior extensão possível e não é necessária nenhuma poda.
-
Por fim, agregue as previsões das árvores de destino para prever novos dados.
O Random Forests é muito eficaz na estimativa de dados ausentes e na manutenção da precisão quando uma grande proporção dos dados está ausente. Ele também pode equilibrar erros em conjuntos de dados em que as classes são desequilibradas. Mais importante ainda, ele pode lidar com conjuntos de dados maciços com grande dimensionalidade. No entanto, uma desvantagem do uso de Random Forests é que você pode facilmente ajustar em excesso conjuntos de dados ruidosos, especialmente no caso de regressão.
Impulsionamento
O reforço é outra abordagem para melhorar as previsões resultantes de uma árvore de decisão. Assim como o bagging e as florestas aleatórias, é uma abordagem geral que pode ser aplicada a muitos métodos de aprendizado estatístico para regressão ou classificação. Lembre-se de que o bagging envolve a criação de várias cópias do conjunto de dados de treinamento original usando o bootstrap, ajustando uma árvore de decisão separada a cada cópia e, em seguida, combinando todas as árvores para criar um único modelo preditivo. Notavelmente, cada árvore é construída em um conjunto de dados bootstrapped, independente das outras árvores.
O Boosting funciona de forma semelhante, exceto pelo fato de que as árvores são cultivadas sequencialmente: cada árvore é cultivada usando informações de árvores cultivadas anteriormente. O Boosting não envolve amostragem bootstrap; em vez disso, cada árvore é ajustada em uma versão modificada do conjunto de dados original.
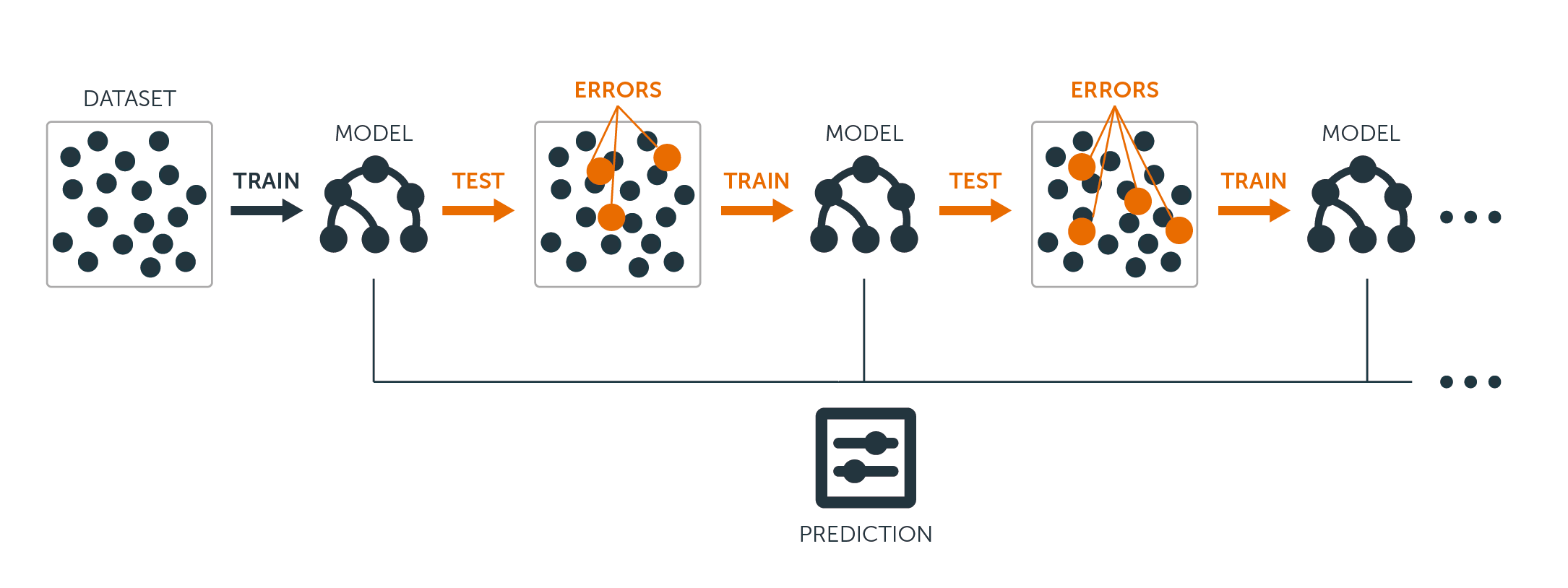
Para árvores de regressão e classificação, o boosting funciona da seguinte forma:
-
Ao contrário do ajuste de uma única árvore de decisão grande aos dados, o que equivale a um ajuste rígido dos dados e, possivelmente, a um ajuste excessivo, a abordagem de reforço aprende lentamente.
-
Dado o modelo atual, você ajusta uma árvore de decisão aos resíduos do modelo. Ou seja, você ajusta uma árvore usando os resíduos atuais, e não o resultado $Y$, como resposta.
-
Em seguida, você adiciona essa nova árvore de decisão à função ajustada para atualizar os resíduos. Cada uma dessas árvores pode ser bem pequena, com apenas alguns nós terminais, determinados pelo parâmetro $d$ no algoritmo. Ao ajustar pequenas árvores aos resíduos, você melhora lentamente o $\hat{f}$ nas áreas em que ele não tem um bom desempenho.
-
O parâmetro de encolhimento $\nu$ torna o processo ainda mais lento, permitindo que mais árvores de formatos diferentes ataquem os resíduos.
O Boosting é muito útil quando você tem muitos dados e espera que as árvores de decisão sejam muito complexas. O Boosting tem sido usado para resolver muitos problemas desafiadores de classificação e regressão, incluindo análise de risco, análise de sentimentos, publicidade preditiva, modelagem de preços, estimativa de vendas e diagnóstico de pacientes, entre outros.
Essencialmente, esses algoritmos combinam as previsões de várias árvores de decisão para melhorar o desempenho geral e a estabilidade. Depois de entender os algoritmos avançados, para o escopo deste tutorial, continuaremos com os modelos simples de árvore de decisão.
Criação de modelos de árvore de decisão passo a passo em R
Aprendemos muita teoria e a intuição por trás dos modelos de árvore de decisão e suas variações, mas nada melhor do que colocar a mão na massa e construir esses modelos, avaliando seu desempenho passo a passo.
Preparação dos dados para modelagem
Para os exemplos a seguir, usaremos o popular Boston Housing Dataset.
O conjunto de dados do Boston Housing contém informações sobre o mercado imobiliário em Boston, Massachusetts, na década de 1970. Ele tem 506 observações e 14 variáveis, incluindo 13 recursos e uma variável-alvo.
Os recursos do conjunto de dados do Boston Housing são:
- CRIM: Taxa de criminalidade per capita por cidade
- ZN: Proporção de terrenos residenciais com zoneamento para lotes acima de 25.000 pés quadrados.
- INDUS: Proporção de acres de negócios não varejistas por cidade
- CHAS: Variável fictícia do Charles River (= 1 se o setor limita o rio; 0 caso contrário)
- NOX: Concentração de óxido nítrico (partes por 10 milhões)
- RM: Número médio de cômodos por residência
- IDADE: Proporção de unidades ocupadas por proprietários construídas antes de 1940
- DIS: Distâncias ponderadas para cinco centros de emprego de Boston
- RAD: Índice de acessibilidade a rodovias radiais
- TAX: Taxa de imposto sobre a propriedade de valor integral por US$ 10.000
- PTRATIO: Relação aluno-professor por cidade
- Negros: proporção de negros por cidade
- LSTAT: Porcentagem do status inferior da população
A variável-alvo é MEDV, que representa o valor médio de residências ocupadas por proprietários em US$ 1.000.
O objetivo é prever o valor médio de casas ocupadas por proprietários (em milhares de dólares) com base nos recursos fornecidos.
No R, os dados são fornecidos em um pacote chamado "MASS". Você terá que instalar vários pacotes para este tutorial e carregá-los. Como isso seria uma repetição, vamos demonstrar esse processo com o pacote MASS uma vez, e você o repetirá sempre que vir um novo pacote usado neste guia.
# install the package
install.packages("MASS")
# Load the MASS package
library(MASS)
# Load the Boston Housing dataset
data(Boston)Muitas vezes, é necessário explorar os dados por meio de visualizações e executar etapas de pré-processamento de dados antes de passar para a modelagem. Vamos dar uma olhada na distribuição das variáveis por meio de histogramas.
Aqui está o código para criá-los:
# Load the library
library(tidymodels)
library(tidyr)
# Prepare the dataset for ggplot2
boston_data_long <- Boston %>%
pivot_longer(cols = everything(),
names_to = "variable",
values_to = "value")
# Create a histogram for all numeric variables in one plot
boston_histograms <- ggplot(boston_data_long, aes(x = value)) +
geom_histogram(bins = 30, color = "black", fill = "lightblue") +
facet_wrap(~variable, scales = "free", ncol = 4) +
labs(title = "Histograms of Numeric Variables in the Boston Housing Dataset",
x = "Value",
y = "Frequency") +
theme_minimal()
# Plot the histograms
print(boston_histograms)E o resultado tem a seguinte aparência:
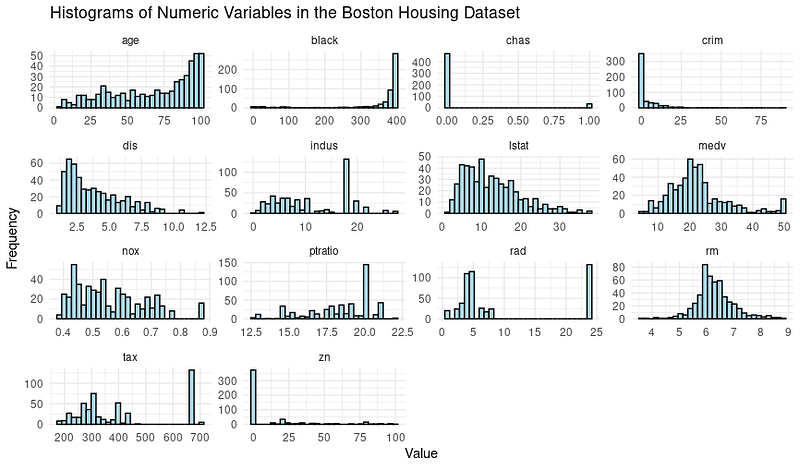
Notamos alguns valores discrepantes, especialmente nas colunas como RAD, TAX e NOX. Nosso objetivo neste tutorial é nos concentrarmos na fase de modelagem da árvore de decisão; portanto, vamos dividir o conjunto de dados em conjuntos de treinamento e de teste.
# Split the data into training and testing sets
set.seed(123)
data_split <- initial_split(Boston, prop = 0.75)
train_data <- training(data_split)
test_data <- testing(data_split)Vamos agora nos aprofundar na modelagem e na avaliação do desempenho do modelo.
Modelagem de árvore de decisão simples
Usando a função decision_tree() do pacote Tidymodels no R, é fácil criar primeiro uma especificação de modelo de árvore de decisão e, em seguida, ajustar o modelo aos dados de treinamento.
# Create a decision tree model specification
tree_spec <- decision_tree() %>%
set_engine("rpart") %>%
set_mode("regression")
# Fit the model to the training data
tree_fit <- tree_spec %>%
fit(medv ~ ., data = train_data)Usamos o modelo de "regressão" aqui e, para uma árvore de decisão de classificação, teríamos que usar o modo de "classificação".
Avaliação do desempenho da modelagem da árvore de decisão
Para avaliar o desempenho do modelo, usaremos o pacote Tidymodels para calcular a raiz do erro quadrático médio (RMSE) e o valor R-quadrado do nosso modelo de árvore de decisão nos dados de teste.
# Make predictions on the testing data
predictions <- tree_fit %>%
predict(test_data) %>%
pull(.pred)
# Calculate RMSE and R-squared
metrics <- metric_set(rmse, rsq)
model_performance <- test_data %>%
mutate(predictions = predictions) %>%
metrics(truth = medv, estimate = predictions)
print(model_performance)Você obterá um resultado que apresenta duas métricas de desempenho: Root Mean Squared Error (RMSE) e R-quadrado (R²).
.metric .estimator .estimate
<chr> <chr> <dbl>
1 rmse standard 5.22
2 rsq standard 0.689Análise dos resultados do modelo
Então, os resultados de nosso modelo são bons o suficiente?
- RMSE (Root Mean Squared Error, erro quadrático médio): Isso mede a diferença média entre os valores previstos e os valores reais. No seu caso, o RMSE é de 5,22, o que significa que, em média, as previsões feitas pelo modelo de árvore de decisão estão defasadas em aproximadamente 5,22 unidades em relação aos valores reais. Um valor menor de RMSE é geralmente melhor, pois indica erros de previsão menores.
- R-quadrado (R²): Isso mede o grau em que o modelo explica a variação na variável-alvo. Ele varia de 0 a 1, sendo que um valor mais alto indica um melhor ajuste. No seu caso, o R² é 0,689, o que significa que o modelo explica aproximadamente 68,9% da variação na variável-alvo (MEDV).
Também podemos otimizar os hiperparâmetros para obter desempenho ou optar por modelos mais complexos, como Random Forests e XGBoost, ao custo da interpretabilidade do modelo.
Previsão de resultados usando o modelo de árvore de decisão
Quando você estiver satisfeito com o modelo, é hora de permitir que ele faça previsões.
Isso é o mesmo que fizemos com os dados de teste usando a função predict(), mas teremos que fornecer um novo conjunto de dados que imite as informações sobre uma nova casa em Boston. Esse é um cenário possível quando o modelo entra em operação em um ambiente de produção.
# Make predictions on new data
new_data <- tribble(
~crim, ~zn, ~indus, ~chas, ~nox, ~rm, ~age, ~dis, ~rad, ~tax, ~ptratio, ~black, ~lstat,
0.03237, 0, 2.18, 0, 0.458, 6.998, 45.8, 6.0622, 3, 222, 18.7, 394.63, 2.94
)
predictions <- predict(tree_fit, new_data)
print(predictions)E você obterá o valor médio previsto (em US$ 1.000) dessa casa específica:
# A tibble: 1 × 1
.pred
<dbl>
1 37.8Com isso, você está equipado com as etapas de construção de um modelo de árvore de decisão - vamos agora nos concentrar em como podemos interpretar o que está acontecendo dentro do modelo para nós mesmos e para o stakeholder que usa a solução que acabamos de construir.
Interpretação da árvore de decisão
A vantagem mais significativa, como dissemos anteriormente, é a interpretabilidade dos modelos de árvore de decisão. Vamos visualizar a árvore de decisão para entender melhor o modelo:
# Load the library
library(rpart.plot)
# Plot the decision tree
rpart.plot(tree_fit$fit, type = 4, extra = 101, under = TRUE, cex = 0.8, box.palette = "auto")Você verá um gráfico como este:
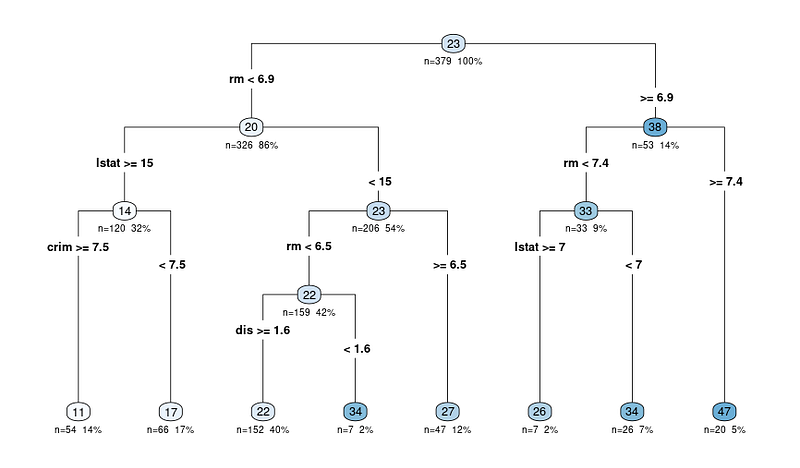
O diagrama de saída da função rpart.plot mostra uma representação de árvore de decisão do modelo. Nesse diagrama, cada nó representa uma divisão na árvore de decisão com base nas variáveis preditoras. O diagrama de saída inclui várias informações que podem nos ajudar a interpretar a árvore de decisão:
Os diagramas de árvore começam com o nó
Os nós são representados por círculos e estão conectados por linhas, mostrando a estrutura hierárquica da árvore de decisão. A árvore começa com um nó raiz no topo e se ramifica em nós internos, levando finalmente aos nós terminais ou folhas na parte inferior.
Os critérios de divisão para cada nó interno
Cada nó interno exibe o critério de divisão, que é a variável preditora e o valor usado para dividir os dados em dois subconjuntos.
Por exemplo, um nó pode mostrar "RM < 6,8", indicando que as observações com um número médio de cômodos por residência (RM) menor que 6,8 seguirão o ramo esquerdo, enquanto as observações com RM maior ou igual a 6,8 seguirão o ramo direito.
N: Número de observações após a divisão
O valor n em cada nó representa o número de observações no conjunto de dados que se enquadram nesse nó específico. Por exemplo, se um nó mostrar "n = 100", isso significa que 100 observações no conjunto de dados atendem aos critérios dos nós pai desse nó.
X%: A proporção do total de observações do conjunto de dados que atingiu o nó específico.
O valor percentual ajuda a entender o tamanho relativo de cada nó em comparação com todo o conjunto de dados, mostrando como os dados estão sendo divididos e distribuídos na árvore. Uma porcentagem mais alta significa que uma proporção maior dos dados seguiu o caminho de decisão que leva ao nó específico, enquanto uma porcentagem mais baixa indica uma proporção menor dos dados que chegam a esse nó.
O valor previsto para cada nó
O valor previsto em cada nó é exibido como um número em um círculo colorido (nó). Em uma árvore de regressão, esse é o valor médio da variável-alvo para todas as observações que se enquadram nesse nó.
Por exemplo, o último nó principal que mostra 47 significa que o valor médio da variável de destino (no nosso caso, o valor médio de residências ocupadas por proprietários) para todas as observações nesse nó é 47.
Comece no nó raiz e siga as ramificações
Portanto, ao interpretar qualquer resultado, você começa no nó raiz e segue as ramificações com base nos critérios de divisão até chegar a um nó terminal. O valor previsto no nó terminal fornece a previsão do modelo para uma determinada observação e a lógica por trás da decisão.
Extração de regras da árvore de decisão
Se ainda preferir extrair as regras em forma de texto (em vez de percorrer o diagrama), você também pode fazer isso usando a mesma biblioteca que usamos para desenhar o diagrama.
Aqui está o código para fazer isso:
rules <- rpart.rules(tree_fit$fit)
print(rules)E você verá um resultado com os valores previstos e as regras que ele segue para chegar a esse valor, conforme abaixo:
medv
11 when rm < 6.9 & lstat >= 15 & crim >= 7.5
17 when rm < 6.9 & lstat >= 15 & crim < 7.5
22 when rm < 6.5 & lstat < 15 & dis >= 1.6
26 when rm is 6.9 to 7.4 & lstat >= 7
27 when rm is 6.5 to 6.9 & lstat < 15
34 when rm < 6.5 & lstat < 15 & dis < 1.6
34 when rm is 6.9 to 7.4 & lstat < 7
47 when rm >= 7.4Agora que você vê as regras, talvez se pergunte como a decisão pode ser tomada com 3-4 variáveis quando alimentamos a árvore de decisão com muito mais variáveis.
Bem, parece que algumas variáveis são mais importantes do que as outras. Vamos entender melhor esse conceito.
Entendendo as variáveis importantes das árvores de decisão
Já descobrimos o diagrama de árvore e como o modelo funciona. Um último aspecto da interpretação é entender as variáveis importantes do conjunto de dados.
Veja por que isso é fundamental:
- Seleção de recursos. A identificação de variáveis importantes pode ajudá-lo a se concentrar em recursos relevantes e, possivelmente, remover os menos importantes, simplificando o modelo e reduzindo o ruído.
- Conhecimento do domínio. Obter insights sobre quais recursos são mais importantes pode ajudá-lo a entender melhor as relações entre as variáveis e a variável-alvo no contexto do seu problema específico.
- Interpretação do modelo. Compreender os principais recursos que orientam as previsões do modelo pode fornecer informações valiosas para o processo de tomada de decisão.
Nas árvores de decisão, a importância da variável é geralmente determinada pelos recursos usados para a divisão nos nós. Os recursos usados para a divisão em uma posição mais alta na árvore ou usados com mais frequência podem ser considerados mais importantes.
A importância de uma variável pode ser quantificada pela redução na medida de impureza (por exemplo, índice de Gini ou erro quadrático médio) que ela traz quando usada para divisão. O pacote "VIP" do R eliminou todas as complexidades, e o gráfico pode ser obtido por meio do código abaixo:
# Load the necessary library
library(vip)
# Create a variable importance plot
var_importance <- vip::vip(tree_fit, num_features = 10)
print(var_importance)E você obterá o gráfico de importância variável abaixo:
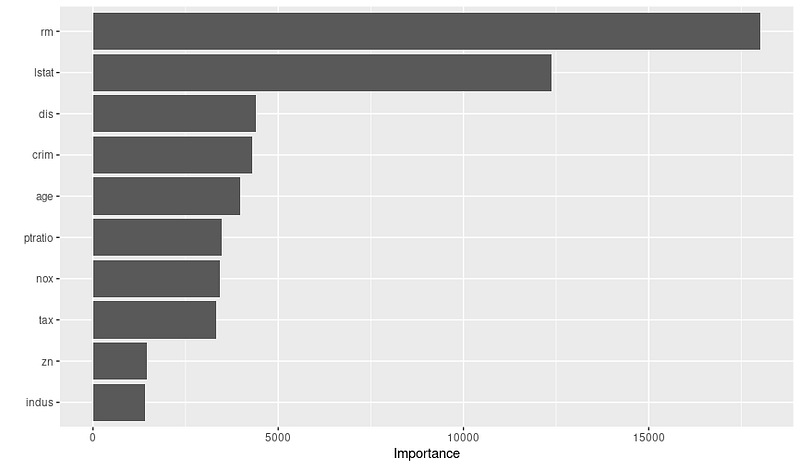
Depois de ver o gráfico, você pode fazer mais pesquisas sobre a importância dessas variáveis, colaborando com especialistas no domínio. Por exemplo, com base no gráfico acima, podemos inferir as três principais variáveis importantes e a justificativa:
- RM: O número médio de cômodos por residência é uma característica altamente crucial, sugerindo que as casas com mais cômodos tendem a ter valores medianos mais altos.
- LSTAT: A porcentagem da população com status socioeconômico mais baixo é outra variável significativa, indicando que os bairros com status mais baixo provavelmente terão valores médios de imóveis mais baixos.
- DIS: A distância ponderada dos centros de emprego é uma variável vital, mostrando que as casas mais próximas dos principais centros de emprego provavelmente terão valores medianos mais altos.
Portanto, lembre-se de verificar o gráfico de importância das variáveis antes de finalizar o modelo; isso pode ajudá-lo a criar e selecionar recursos melhores para otimizar o desempenho.
Conclusão
Neste tutorial, exploramos os conceitos fundamentais das árvores de decisão e abordamos não apenas a criação de modelos, mas também a interpretação deles. As árvores de decisão são modelos poderosos e interpretáveis para tarefas de classificação e regressão, o que as torna uma ferramenta essencial no arsenal de um cientista de dados.
À medida que você continua a desenvolver suas habilidades, nós o incentivamos a se aprofundar no mundo das árvores de decisão, explorar algoritmos alternativos e aprimorar suas habilidades de programação em R. Aqui estão alguns recursos para sua próxima etapa:
- Fundamentos de aprendizado de máquina em R
- Introdução à engenharia de recursos em R
- Modelagem com Tidymodels em R
- Aprendizado de máquina com modelos baseados em árvores no R
Sem dúvida, a expansão do seu conhecimento e a experimentação de novas ferramentas e técnicas permitirão que você enfrente diversos desafios e forneça insights valiosos para seus projetos.


