Tutorial do Adam Optimizer: Intuição e implementação em Python

O que é o Adam Optimizer? A resposta curta

Adam, que significa Adaptive Moment Estimation (Estimativa de momento adaptável), é um algoritmo de otimização popular usado em machine learning e, mais frequentemente, em aprendizagem profunda. 

Adam combina as principais ideias de duas outras técnicas de otimização robusta: momentum e RMSprop. Ele é denominado adaptativo, pois ajusta a taxa de aprendizado para cada parâmetro.

Aqui estão seus principais recursos e vantagens:

• Adaptividade: O Adam adapta a taxa de aprendizado para cada parâmetro, o que pode acelerar o aprendizado em muitos casos.
• Momentum: Ele usa uma forma de impulso, ajudando-o a navegar em superfícies complexas, como ravinas e pontos de sela, de forma mais eficaz.
• Correção de viés: O Adam inclui termos de correção de viés, que o ajudam a ter um bom desempenho mesmo nos estágios iniciais do treinamento.
• Eficiência computacional: É relativamente eficiente em termos de computação e requer pouca memória.
• Robustez do hiperparâmetro: Embora a taxa de aprendizado possa precisar de ajuste, o Adam costuma ser menos sensível às escolhas de hiperparâmetros do que alguns outros otimizadores.

Em resumo, a Adam faz com que os modelos aprendam de forma mais eficiente, ajustando continuamente a taxa de aprendizagem de cada parâmetro e, como consequência, tende a convergir muito mais rapidamente do que a descida de gradiente estocástica padrão. Para muitos aplicativos de aprendizagem profunda, ele é, portanto, uma escolha padrão forte.

Algoritmos de pré-requisito

O Adam unifica as principais ideias de alguns outros algoritmos de otimização críticos, reforçando suas vantagens e, ao mesmo tempo, abordando suas deficiências. Você precisará revisá-las antes de entender a intuição por trás do Adam e implementá-la em Python.

Analogia de otimização

Para entender a intuição por trás desses algoritmos de otimização, vamos continuar nossa analogia da introdução. 

Imagine que você está com os olhos vendados em uma região complicada e montanhosa. Você foi encarregado de encontrar o ponto mais baixo desse terreno. A inclinação do terreno representa a função de perda função de perda de um modelo de machine learning. O ponto "mais baixo" geral (mínimo global) é a solução ideal para o sistema.

Agora, vamos ligar alguns pontos: Sua posição atual no terreno representa o estado atual dos parâmetros do modelo. A altura em qualquer ponto representa o valor de perda para esses parâmetros. A maneira como você está navegando também corresponde ao ajuste dos parâmetros do modelo em um sentido matemático.

Todo algoritmo de otimização é como uma estratégia para navegar com sucesso no cenário desse problema, orientando o solucionador sobre onde dar o próximo passo e qual deve ser o tamanho desses passos. Alguns algoritmos examinam toda a área antes de decidir o próximo movimento, enquanto outros dependem de informações limitadas para serem mais rápidos. 

Ainda assim, outros algoritmos usam ferramentas como o momentum e a adaptação do tamanho da etapa; um bom solucionador sabe quando deve avançar em um problema e quando deve ir com calma.

Descida de gradiente

Descida de gradiente é o Santo Graal da otimização em machine learning, pois define a base para muitos algoritmos que você pode desenvolver.

Se você usar o Gradient Descent (GD), sentirá cuidadosamente toda a área ao seu redor (usando o conjunto de dados completo) antes de dar cada passo. Esse exame minucioso permite que você tome decisões muito precisas sobre o caminho a seguir, mas isso leva muito tempo. Você sempre se move na direção da descida mais íngreme, o que significa que você sempre se moverá em direção ao solo mais baixo. No entanto, se você chegar a uma pequena depressão (o mínimo local), poderá ficar preso ali, incapaz de detectar que há um ponto ainda mais baixo em outro lugar.

Principais recursos do GD:

• Usa todo o conjunto de dados para cada etapa
• Consistente, mas potencialmente lento
• Pode ficar preso em mínimos locais

Descida de Gradiente Estocástico (SGD)

Nesse cenário, você está com pressa e não tem tempo para sentir toda a região ao seu redor. Em vez disso, você verifica apenas um ponto aleatório próximo aos seus pés (um ponto de dados). Isso torna cada etapa mais rápida, mas menos precisa. Você também pode verificar um pequeno lote de pontos, o que é conhecido como descida de gradiente em minilote, que abordaremos mais adiante. 

Seu caminho é mais irregular do que o da descida gradiente; na verdade, às vezes ele se parece com o caminho de um marinheiro bêbado. Ocasionalmente, você pode subir uma ladeira. Esse caminho ruidoso pode ser, na verdade, a maior vantagem: é muito provável que você escape dos mínimos locais. 

Mas, à medida que você se aproxima do fundo, precisa dar passos menores (diminuir a taxa de aprendizado) para evitar ultrapassar o ponto mais baixo.

Principais recursos do SGD:

• Usa apenas um ponto de dados aleatório para cada etapa
• Iterações mais rápidas, mas um caminho mais ruidoso
• Você pode escapar de mínimos locais com mais facilidade
• A taxa de aprendizado geralmente precisa ser reduzida com o tempo

Observação: Neste ponto, recomendo que você leia nosso artigo separado sobre artigo separado sobre GD e SGDpois ele aborda os detalhes desses dois algoritmos críticos com muito mais profundidade. Isso também ajudará você a entender melhor a próxima seção de codificação.

SGD com impulso

Agora você está em um skate entre as colinas. Quando você empurra em uma direção, o impulso do skate o mantém praticamente na mesma direção por um tempo. 

Esse momentum é como uma média móvel de suas direções anteriores. Ele ajuda você a passar por pequenos solavancos e depressões locais, talvez até mesmo ajudando-o a encontrar um ponto de menor elevação mais adiante. 

Se você estiver se movendo em uma direção por algum tempo, o impulso aumenta e você vai mais rápido. Dessa forma, você pode convergir para o ponto mais baixo mais rapidamente, especialmente em terrenos com uma inclinação descendente consistente.

Principais recursos do SGD with Momentum:

• Acumula uma média móvel de gradientes anteriores
• Ajuda a navegar além das pequenas variações locais
• Pode levar a uma convergência mais rápida

RMSprop (Propagação da raiz quadrada média)

Pense em ter calçados de alta tecnologia que possam ajustar a aderência com base no terreno em que você está andando. Esses sapatos programam o gradiente do solo em cada direção, mantendo uma média exponencialmente decrescente de gradientes quadrados. Em áreas onde a inclinação muda muito, o calçado oferece mais aderência, permitindo que você dê passos menores e mais cuidadosos. Em áreas mais suaves com inclinações consistentes, os tênis proporcionam a você passos mais longos. 

Esse "tamanho do passo" adaptável ajuda você a navegar com eficiência em declives íngremes e rasos, evitando que você dê um passo muito grande em uma área íngreme ou um passo muito pequeno em uma área plana.

Principais recursos do RMSprop:

• Taxas de aprendizagem adaptativas para cada parâmetro
• Divide a taxa de aprendizado por uma média exponencialmente decrescente de gradientes quadrados
• Ajuda a navegar em áreas com diferentes inclinações

A intuição por trás do Adam Optimizer

O Adam é como combinar seu skate (momentum) com seus tênis adaptáveis (RMSprop) e adicionar um sistema de navegação inteligente à mistura.

A parte do skate (impulso) mantém você na direção geral correta. Isso significa que, em regiões de declive, suaves e consistentes, Adam permite que você se mova rapidamente. Em terrenos difíceis e variáveis, ele ajuda você a manter um ritmo constante, mas cauteloso.

Os tênis adaptáveis (RMSprop) detectam onde você está indo e ajustam a aderência do skate. O sistema de navegação inteligente (correção de inclinação) no Adam é especialmente importante no início da sua viagem, quando você parte de um ponto aleatório e não sabe muito sobre o terreno.

Essa combinação de atributos é a razão pela qual o Adam frequentemente encontra o ponto mais baixo (a solução para o problema) de forma muito eficiente e porque sua estrutura pode lidar bem com diferentes tipos de terreno (diferentes tipos de problemas de machine learning).

Principais recursos do Adam:

• Combina ideias de momentum e RMSprop
• Mantém uma média exponencialmente decrescente de gradientes passados e gradientes passados ao quadrado
• Taxas de aprendizagem adaptativas para cada parâmetro
• Correção de viés para as etapas iniciais

Como você observou, cada um dos algoritmos mencionados se baseia nos anteriores, com o objetivo de otimizar o processo de encontrar o ponto mais baixo, abordando diferentes desafios encontrados em vários tipos de problemas de otimização.

Adam vs. Outros algoritmos de otimização

Antes de entrarmos nos detalhes da implementação do Adam e dos outros algoritmos mencionados, deixe-me compartilhar com você uma tabela de resumo comparando o tempo de execução e o desempenho do RMSE de cada um em um problema de regressão de amostra:

import pandas as pd
# Disable scientific notation
pd.set_option("display.float_format", "{:.4f}".format)
comparison_table = pd.read_csv('optimization_results.csv')
comparison_table

Essa tabela não faz jus à grande diferença entre Adam e os demais, então vou elaborar um gráfico de barras:

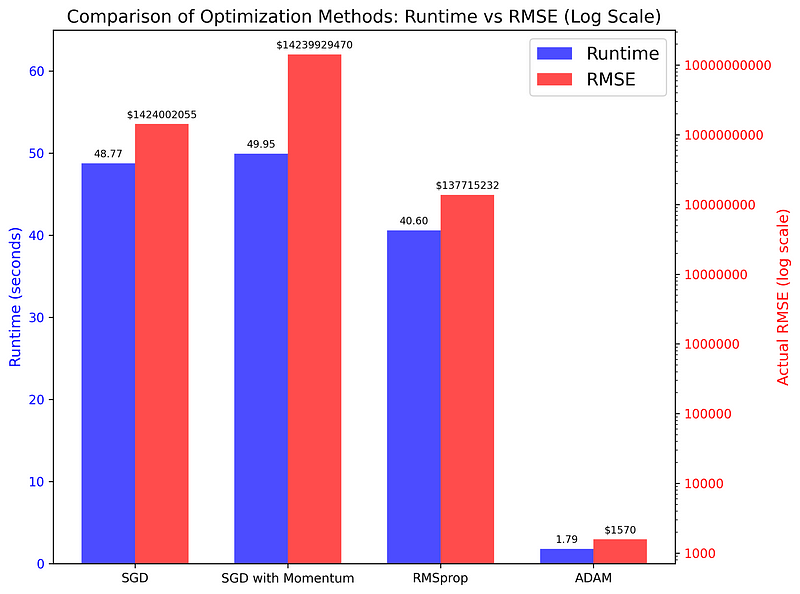
O gráfico compara o tempo de execução e as pontuações de RMSE dos quatro algoritmos usados em uma tarefa de regressão simples. Como você pode ver, as diferenças são surpreendentes (lembre-se de que o eixo direito está em uma escala logarítmica), indicando que o Adam é a melhor opção para a maioria das tarefas de otimização.

Mais adiante, veremos o código que gerou a tabela e o gráfico.

Implementando o Adam Optimizer em Python

Agora que abordamos os conceitos de pré-requisito do Adam e sua intuição, podemos começar a implementá-los em Python. Ao longo do caminho, explicaremos todos os cálculos necessários para que você entenda a implementação. Vamos desenvolver o código passo a passo, começando com o Stochastic Gradient Descent.

Implementação do SGD com minilotes

Anteriormente, mencionamos que o SGD usa apenas um único ponto de dados para decidir o próximo passo. Na prática, essa versão vanilla do SGD raramente é usada, pois seus resultados podem ser ruidosos (seu caminho nas colinas é irregular). 

Para atenuar isso, os profissionais costumam usar uma variação chamada Mini-Batch Gradient Descent, que usa lotes de pontos de dados, como 32, 64 ou 128, antes de dar cada passo (isso é como escanear um caminho estreito em vez da visão de 360 graus antes de dar um passo). 

Portanto, criaremos o código básico para o Adam com essa versão do SGD.

Para manter o código o mais simples possível, escolheremos um pequeno problema de regressão: prever os preços dos diamantes com base em suas medidas em quilates.

Primeiro, vamos importar as bibliotecas necessárias:

import seaborn as sns
import numpy as np
import pandas as pd
import warnings
warnings.filterwarnings("ignore")
np.random.seed(42)

Em seguida, carregamos o conjunto de dados Diamonds do Seaborn, coletamos uma amostra dele e criamos os conjuntos de recursos e alvos:

# Load the data
dataset_size = 20_000
diamonds = sns.load_dataset("diamonds")
# Extract the target and the feature
xy = diamonds[["carat", "price"]].values
np.random.shuffle(xy)  # Shuffle the data
xy = xy[:dataset_size]
xy.shape

Output:
(20000, 2)

A regressão linear exige que você normalize os dados:

# Normalize the data
mean = np.mean(xy, axis=0)
std = np.std(xy, axis=0)
xy_normalized = (xy - mean) / std

Agora, podemos dividir os dados para criar conjuntos de treinamento e de teste:

# Split the data
train_size = int(0.8 * dataset_size)
train_xy, test_xy = xy[:train_size], xy[train_size:]
train_xy.shape

(16000, 2)

Para resolver a tarefa, temos uma série de modelos à nossa disposição, mas, para simplificar, escolheremos a Regressão Linear Simples e a definiremos como uma função:

def model(m, x, b):
   """
   Simple Linear Regression: f(x) = m * x + b, where
   - x: diamond carat
   - m: price increase per carat
   - b: base diamond price
   - f(x): predicted diamond price
   """
  
   return m * x + b

Nosso modelo de regressão linear tem apenas dois parâmetros, m e bportanto, a tarefa do SGD (e, posteriormente, do Adam) é encontrar os valores ideais para eles.

Também devemos definir a função de perda, o erro quadrático médio, que será minimizado por nossos algoritmos:

def mean_squared_error(y_true, y_pred):
   """
   MSE as a loss function. It is defined as:
   Loss = (1/n) * Σ((y - f(x))²), where:
   - n: the length of the dataset
   - y: the true diamond price
   - f(x): predicted diamond price, i.e. m*x + b
   """
   return np.mean((y_true - y_pred) ** 2)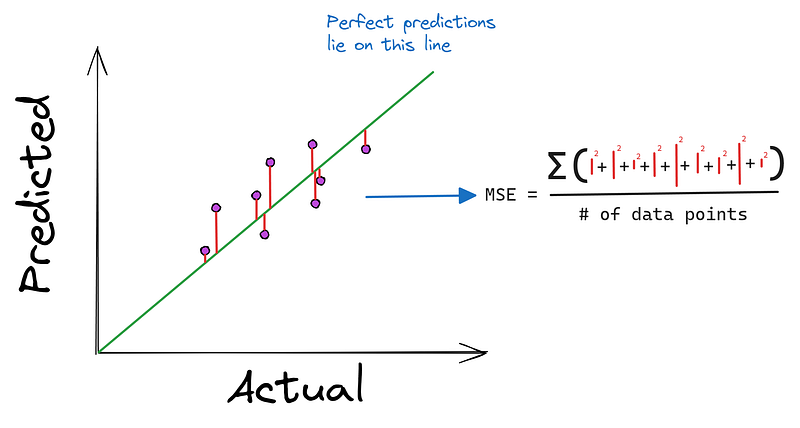

Agora, definimos uma função chamada stochastic_gradient_descent que aceita seis argumentos:

• x e y representam o recurso único e o alvo em nosso problema.
• epochs indica quantas vezes queremos executar a descida (mais sobre isso adiante).
• learning_rate é o tamanho da etapa.
• batch_size para controlar a frequência com que fazemos atualizações de parâmetros
• stopping_threshold define o valor mínimo no qual a perda deve diminuir em cada etapa

def stochastic_gradient_descent(
   x, y, epochs=100, learning_rate=0.01, batch_size=32, stopping_threshold=1e-6
):
   """
   SGD with support for mini-batches.
   """
   # Initialize the model parameters randomly
   m = np.random.randn()
   b = np.random.randn()
   n = len(x)  # The number of data points
   previous_loss = np.inf

Dentro da função, primeiro inicializamos os parâmetros que queremos otimizar com valores aleatórios (começando em um local aleatório nas colinas). Também definimos a perda inicial como infinita, representando o estado não resolvido do nosso problema.

Em seguida, iniciamos um loop for que é executado para epochs iterações. Dentro do loop, embaralhamos os dados para evitar que você aprenda padrões dependentes de ordem nos dados:

def stochastic_gradient_descent(...):
   ...
   for i in range(epochs):
       # Shuffle the data
       indices = np.random.permutation(n)
       x = x[indices]
       y = y[indices]

Em seguida, iniciamos outro loop controlado pelo parâmetro batch_size e extraímos o lote atual:

def stochastic_gradient_descent(...):
   ...
   for i in range(epochs):
       ...
       for j in range(0, n, batch_size):
           # Extract the current batch
           x_batch = x[j:j + batch_size]
           y_batch = y[j:j + batch_size]

Dentro desse loop interno, calculamos os gradientes (derivadas parciais) para ambos os parâmetros (indicando onde precisamos dar o próximo passo):

def stochastic_gradient_descent(...):
   ...
   for i in range(epochs):
       ...
       for j in range(0, n, batch_size):
           # Extract the current batch
           ...
           # Make predictions with current m, b
           y_pred = model(m, x_batch, b)
           # Compute the gradients
           m_gradient = 2 * np.mean(x_batch * (y_batch - y_pred))
           b_gradient = 2 * np.mean(y_batch - y_pred)

Depois de calcular os gradientes, há uma etapa crítica de recorte dos gradientes:

def stochastic_gradient_descent(...):
   ...
   for i in range(epochs):
       ...
       for j in range(0, n, batch_size):
           # Extract the current batch
           ...
           # Compute the gradients
           ...
           # Gradient clipping
           clip_value = 1.0
           m_gradient = np.clip(m_gradient, -clip_value, clip_value)
           b_gradient = np.clip(b_gradient, -clip_value, clip_value)

O recorte de gradiente evita a comum gradientes explosivos em que a magnitude dos gradientes se aproxima do infinito.

Após o recorte, atualizamos os parâmetros usando a taxa de aprendizado (damos um passo na direção dos gradientes controlados pela taxa de aprendizado):

def stochastic_gradient_descent(...):
   ...
   for i in range(epochs):
       ...
       for j in range(0, n, batch_size):
           # Extract the current batch
           ...
           # Compute the gradients
           ...
           # Gradient clipping
           ...
           # Update the model parameters
           m -= learning_rate * m_gradient
           b -= learning_rate * b_gradient

Agora, no loop pai (após todos os lotes terem sido explorados), calculamos a perda para a época atual (veja o quanto descemos em relação à nossa posição inicial):

def stochastic_gradient_descent(...):
   ...
   for i in range(epochs):
       ...
       for j in range(0, n, batch_size):
           # Extract the current batch
           ...
           # Compute the gradients
           ...
           # Gradient clipping
           ...
           # Update the model parameters
           ...
       # Compute the epoch loss
       y_pred = model(m, x, b)
       current_loss = loss(y, y_pred)

Se a perda de época for menor que o valor de stopping_thresholdinterromperemos todo o processo:

def stochastic_gradient_descent(...):
   ...
   for i in range(epochs):
       ...
       for j in range(0, n, batch_size):
           # Extract the current batch
           ...
           # Compute the gradients
           ...
           # Gradient clipping
           ...
           # Update the model parameters
           ...
       # Compute the epoch loss
       ...
       # Check against the stopping threshold
       if abs(previous_loss - current_loss) < stopping_threshold:
           break
       previous_loss = current_loss

No final (depois que as épocas se esgotam ou o limite de parada é atingido), retornamos m e b, que agora estão otimizados:

def stochastic_gradient_descent(...):
   ...
   for i in range(epochs):
       ...
       for j in range(0, n, batch_size):
           # Extract the current batch
           ...
           # Compute the gradients
           ...
           # Gradient clipping
           ...
           # Update the model parameters
           ...
       # Compute the epoch loss
       ...
       # Check against the stopping threshold
       ...
   return m, b

SGD com impulso

Agora, vamos adicionar momentum ao SGD. O código dessa versão não é muito diferente da versão em mini-lote.

Definimos uma nova função com um parâmetro momentum parâmetro:

def stochastic_gradient_descent_with_momentum(
       x, y, epochs=100, learning_rate=0.01, batch_size=32,
       stopping_threshold=1e-6, momentum=0.9
):
   """
   SGD with momentum and support for mini-batches.
   """
   # Initialize the model parameters randomly
   m = np.random.randn()
   b = np.random.randn()
   # Initialize velocity terms
   v_m = 0
   v_b = 0
  
   n = len(x)
   previous_loss = np.inf

Dentro da função, definiremos mais duas variáveis, v_m e v_b,, para manter o controle dos gradientes acumulados que servirão como nosso impulso. Nós os definimos como 0 no início, já que não temos nenhum impulso no início do algoritmo.

Em seguida, o restante do código é o mesmo até o momento em que recortamos os gradientes:

def sgd_with_momentum(...):
   ...
   for i in range(epochs):
       ...
       for j in range(0, n, batch_size):
           # Extract the current batch
           ...
           # Compute the gradients
           ...
           # Gradient clipping
           ...
           # Update velocity terms
           v_m = momentum * v_m + learning_rate * m_gradient
           v_b = momentum * v_b + learning_rate * b_gradient
           # Update the model parameters using velocity
           m -= v_m
           b -= v_b

Depois que os gradientes são cortados, usamos a regra de atualização do momento para modificar os termos de velocidade. Aqui está uma visão de nível superior do código:

# Initialize
v_m = 0
v_b = 0
...
# Update velocity terms
v_m = momentum * v_m + learning_rate * m_gradient
v_b = momentum * v_b + learning_rate * b_gradient
# Update the model parameters using velocity
m -= v_m
b -= v_b

A velocidade v_* acumula gradientes ao longo do tempo. Isso significa que, se estivermos nos movendo em uma direção consistente, aumentaremos a velocidade nessa direção.

Em áreas onde o gradiente muda rapidamente (como vales estreitos no cenário de perda), o impulso ajuda a amortecer as oscilações. Desenvolvemos inércia suficiente para não ficarmos presos em pequenas variações locais, como mínimos locais ou pontos de sela.

A partemomentum * v_m é o que acumula os gradientes. Por exemplo, se tivermos um gradiente positivo grande, sua velocidade será igualmente grande, e a atualização do parâmetro será ainda maior. Portanto, um momentum de 0,9 significa que preservamos 90% da velocidade da mudança anterior para a próxima etapa. Em cada etapa N, usaremos 90% da velocidade total dos gradientes das etapas N-1.

Neste ponto, recomendo que você crie alguns valores aleatórios para m e b e seus gradientes e use a regra de atualização do momento para ver como os parâmetros mudam se você for para cima ou para baixo.

RMSprop

Agora, vamos ver a implementação do RMSprop. Como o SGD com impulso, a principal mudança ocorre ao fazer atualizações de parâmetros.

Primeiro, definimos uma nova função com dois parâmetros adicionais, beta e epsilon (sem momentum):

def rmsprop_optimization(
   x, y, epochs=100, learning_rate=0.01, batch_size=32,
   stopping_threshold=1e-6, beta=0.9, epsilon=1e-8,
):
   """
   RMSprop optimization with support for mini-batches.
   """
   # Initialize the model parameters randomly
   m = np.random.randn()
   b = np.random.randn()
   # Initialize accumulators for squared gradients
   s_m = 0
   s_b = 0
   n = len(x)
   previous_loss = np.inf

Além disso, dentro da função, criamos duas novas variáveis para acumular gradientes ao quadrado, s_m e s_b.

Agora, quando chegarmos ao estágio de atualização, recalcularemos os gradientes quadrados e atualizaremos os parâmetros:

def rmsprop_optimization(...):
   ...
   for i in range(epochs):
       ...
       for j in range(0, n, batch_size):
           # Extract the current batch
           ...
           # Compute the gradients
           ...
           # RMSprop doesn't need gradient clipping
           # Update accumulators
           s_m = beta * s_m + (1 - beta) * (m_gradient**2)
           s_b = beta * s_b + (1 - beta) * (b_gradient**2)
           # Update parameters
           m -= learning_rate * m_gradient / (np.sqrt(s_m) + epsilon)
           b -= learning_rate * b_gradient / (np.sqrt(s_b) + epsilon)
           # The rest of the code is the same

Aqui, vemos dois novos parâmetros em uso:

• epsilon é um valor pequeno, normalmente 1e-8, para evitar a divisão por zero ao fazer atualizações.
• beta é o parâmetro da taxa de decaimento, geralmente em torno de 0,9.

O parâmetrobeta controla a quantidade de histórico que consideramos. Um beta mais alto significa que temos uma visão de longo prazo dos gradientes passados, enquanto um beta mais baixo torna o algoritmo mais sensível aos gradientes recentes.

Você não precisa se preocupar com a matemática por trás da regra de atualização do RMSprop. O importante é a lógica por trás deles.

Essencialmente, o que as quatro linhas acima estão fazendo é:

1. Adaptar a taxa de aprendizagem para cada parâmetro, o que é fundamental, pois parâmetros diferentes podem exigir taxas de aprendizagem diferentes.
2. Lidar com o problema do "gradiente de desaparecimento", comum em redes neurais, em que os gradientes se tornam muito pequenos devido à retropropagação. Esse efeito é atenuado pela normalização dos gradientes.
3. Equilibrar o tamanho da etapa:

• Para parâmetros com gradientes grandes (atualizados com frequência), a soma do gradiente ao quadrado no denominador será grande, reduzindo a taxa de aprendizado efetiva.
• Para parâmetros com gradientes pequenos (atualizados com pouca frequência), o denominador será menor, aumentando a taxa de aprendizado efetiva.

Na prática, o RMSprop costuma ter um desempenho melhor do que o SGD básico ou o SGD com momentum, especialmente para problemas de otimização não convexos encontrados com frequência na aprendizagem profunda.

A implementação final: Adam em Python

Novamente, definimos uma nova função:

def adam_optimization(
   x,
   y,
   epochs=100,
   learning_rate=0.001,
   batch_size=32,
   stopping_threshold=1e-6,
   beta1=0.9,
   beta2=0.999,
   epsilon=1e-8,
):
   """
   Adam optimization with support for mini-batches.
   """
   # Initialize the model parameters
   m = np.random.randn()
   b = np.random.randn()
   # Initialize first and second moment vectors
   m_m, v_m = 0, 0
   m_b, v_b = 0, 0
   n = len(x)
   previous_loss = np.inf
   t = 0  # Initialize timestep

Desta vez, definimos cinco novas variáveis para capturar os vetores de primeiro e segundo momentos e a etapa de tempo. No contexto de Adão:

1. O primeiro vetor de momento (m):

• É uma estimativa da média (primeiro momento) dos gradientes.
• Calculado como uma média exponencialmente decrescente de gradientes anteriores.
• Ajuda a estimar a direção do gradiente.

2. O vetor do segundo momento (v):

• É uma estimativa da variação não centralizada (segundo momento) dos gradientes.
• Também calculado como uma média de decaimento exponencial, mas de gradientes ao quadrado.
• Ajuda a adaptar a taxa de aprendizado para cada parâmetro.

Então, o código continua o mesmo até depois de calcularmos os gradientes (não precisamos recortá-los para o Adam):

def adam_optimization(...):
   ...
   for i in range(epochs):
       ...
       for j in range(0, n, batch_size):
           # Extract the current batch
           ...
           # Compute the gradients
           ...
           # Adam doesn't need gradient clipping
          
           # Update biased first moment estimate
           m_m = beta1 * m_m + (1 - beta1) * m_gradient
           m_b = beta1 * m_b + (1 - beta1) * b_gradient
           # Update biased second raw moment estimate
           v_m = beta2 * v_m + (1 - beta2) * (m_gradient**2)
           v_b = beta2 * v_b + (1 - beta2) * (b_gradient**2)
           # Compute bias-corrected first moment estimate
           m_m_hat = m_m / (1 - beta1**t)
           m_b_hat = m_b / (1 - beta1**t)
           # Compute bias-corrected second raw moment estimate
           v_m_hat = v_m / (1 - beta2**t)
           v_b_hat = v_b / (1 - beta2**t)
           # Update parameters
           m -= learning_rate * m_m_hat / (np.sqrt(v_m_hat) + epsilon)
           b -= learning_rate * m_b_hat / (np.sqrt(v_b_hat) + epsilon)
       # The rest of the code is the same

Novamente, peço que você não se preocupe com essas linhas de código, pois elas envolvem muita matemática. Na prática, você nunca precisará implementar o Adam do zero, pois tudo o que você precisa saber é a intuição por trás da regra de atualização.

O primeiro momento age como um impulso, acumulando gradientes anteriores para dar à otimização um senso de direção e velocidade. Isso ajuda Adam a se mover mais rapidamente em direções consistentes e amortece as oscilações em cenários de gradiente ruidosos.

O segundo momento, como no RMSprop, adapta a taxa de aprendizado para cada parâmetro. Ele normaliza efetivamente as atualizações de parâmetros, tornando o aprendizado mais lento para parâmetros com gradientes grandes e acelerando-o para aqueles com gradientes pequenos. Isso permite que Adam manipule parâmetros em diferentes escalas de forma eficaz.

Adam também incorpora a correção de viés para essas médias móveis, o que é particularmente importante nos estágios iniciais do treinamento. Essa correção ajuda Adam a começar com tamanhos de etapas mais precisos, o que pode levar a um progresso inicial mais rápido.

Ao combinar esses elementos, o Adam geralmente alcança uma convergência mais rápida do que os métodos de otimização mais simples. Ele é particularmente eficaz em problemas com gradientes ruidosos, objetivos não estacionários ou conjuntos de dados muito grandes. A natureza adaptativa do Adam o torna relativamente insensível à taxa de aprendizado inicial, exigindo, muitas vezes, menos ajuste de hiperparâmetros do que outros métodos.

Criando uma tabela de comparação de otimizadores

Agora, vamos ver como você pode gerar a tabela de resumo que vimos anteriormente:

comparison_table

Definimos uma função chamada run_optimization para treinar um modelo de regressão linear usando nossas funções de otimização. A função também capturará as pontuações de tempo de execução e RMSE:

import time
def run_optimization(opt_func, x, y, **kwargs):
   # Start a timer
   start_time = time.time()
  
   # Run the optimization function
   m, b = opt_func(x, y, **kwargs)
  
   # End the timer
   end_time = time.time()
   # Run the model on the test set with found parameters
   y_preds = model(m, test_xy[:, 0], b)
   y_preds_denormalized = y_preds * std[1] + mean[1]
   y_true_denormalized = test_xy[:, 1] * std[1] + mean[1]
  
   # Compute MSE and RMSE
   actual_mse = np.mean((y_true_denormalized - y_preds_denormalized) ** 2)
   return end_time - start_time, np.sqrt(actual_mse)

Agora, chamaremos essa função quatro vezes para cada uma de nossas funções de otimização, armazenando os resultados em uma lista em que cada item é uma tripla (nome do algoritmo, tempo de execução em segundos, pontuação RMSE):

# Run all optimization methods
results = []
results.append(
   (
       "SGD",
       *run_optimization(
           stochastic_gradient_descent,
           train_xy[:, 0],
           train_xy[:, 1],
           learning_rate=0.1,
           epochs=10000,
           batch_size=64,
       ),
   )
)
results.append(
   (
       "SGD with Momentum",
       *run_optimization(
           stochastic_gradient_descent_with_momentum,
           train_xy[:, 0],
           train_xy[:, 1],
           learning_rate=0.1,
           epochs=10000,
           batch_size=64,
           momentum=0.9,
       ),
   )
)
results.append(
   (
       "RMSprop",
       *run_optimization(
           rmsprop_optimization,
           train_xy[:, 0],
           train_xy[:, 1],
           learning_rate=0.01,
           epochs=10000,
           batch_size=64,
           beta=0.9,
           epsilon=1e-8,
       ),
   )
)
results.append(
   (
       "Adam",
       *run_optimization(
           adam_optimization,
           train_xy[:, 0],
           train_xy[:, 1],
           learning_rate=0.01,
           epochs=10000,
           batch_size=64,
           beta1=0.9,
           beta2=0.999,
           epsilon=1e-8,
       ),
   )
)

Para uma comparação justa, mantemos a taxa de aprendizado, o número de épocas e o tamanho do lote iguais.

Depois disso, podemos criar nossa tabela:

from tabulate import tabulate  # pip install tabulate
# Create and print the table
headers = ["Optimization Method", "Runtime (seconds)", "Actual RMSE"]
print(tabulate(results, headers=headers, floatfmt=".4f"))
# Save the table
pd.DataFrame(results, columns=headers).to_csv("optimization_results.csv", index=False)

Aqui está o resultado final:

Optimization Method      Runtime (seconds)       Actual RMSE
---------------------  -------------------  ----------------
SGD                                49.9305   1424002054.8658
SGD with Momentum                  50.7744  14239929470.0458
RMSprop                            41.9895    137715232.4602
Adam                                1.8462         1570.1177

Antes de continuar, recomendo que você brinque com os parâmetros de cada função de otimização. É provável que você possa tornar cada um deles, especialmente o Adam, ainda mais rápido e preciso, ajustando a taxa de aprendizado, aumentando o tamanho do lote ou controlando a tendência.

Consulte a seção de conclusão para obter links para o código completo do script de comparação e como criar o gráfico que vimos no início.

Usando o Adam no PyTorch

Para usar o Adam na prática, você não precisa ler um artigo longo como este e escrevê-lo do zero. Sua implementação no PyTorch é mais do que adequada para qualquer tarefa de aprendizagem supervisionada na aprendizagem profunda.

Aqui está um trecho curto e básico que descreve um fluxo de trabalho típico do PyTorch que usa o Adam do módulo torch.optim módulo:

# Import necessary modules
import torch
import torch.nn as nn
import torch.optim as optim
# Define your model
model = nn.Sequential(
   nn.Linear(10, 50),
   nn.ReLU(),
   nn.Linear(50, 1)
)
# Initialize Adam optimizer
optimizer = optim.Adam(model.parameters(), lr=0.001, betas=(0.9, 0.999), eps=1e-08, weight_decay=0)
# Training loop
for epoch in range(num_epochs):
   for batch in dataloader:
       # Zero the gradients
       optimizer.zero_grad()
      
       # Forward pass
       outputs = model(batch)
       loss = criterion(outputs, targets)
      
       # Backward pass
       loss.backward()
      
       # Update weights
       optimizer.step()
# Adjusting learning rate
scheduler = optim.lr_scheduler.StepLR(optimizer, step_size=30, gamma=0.1)
for epoch in range(num_epochs):
   train(...)
   scheduler.step()

Para saber mais sobre o uso do PyTorch em geral e seus algoritmos de otimização, confira este curso introdutório do DataCamp:

• Introdução ao aprendizado profundo no curso PyTorch | DataCamp

Conclusão

Neste artigo, aprendemos os prós e contras do popular otimizador Adam. Começamos intuindo-o primeiro, por meio de discussões sobre seus algoritmos fundamentais, como gradient descent, SGD e RMSprop. Vimos como o Adam combina as principais ideias desses algoritmos, resultando em um algoritmo altamente flexível e de alto desempenho.

Em seguida, abordamos como você pode implementar o Adam Optimizer em Python usando apenas o NumPy. Assim como sua intuição, desenvolvemos o código a partir dos algoritmos fundamentais, desde a descida de gradiente em minibatch, passando pelo RMSprop até o Adam. Também observamos uma diferença impressionante entre o Adam e outros algoritmos em termos de velocidade e desempenho, criando um script simples de benchmarking.

No final, mostramos como usar o Adam no PyTorch, exatamente como você faria na prática, para resolver problemas de aprendizagem profunda. Aqui estão alguns links para os scripts que usamos no tutorial:

• Implementação de SGD em mini-lotes
• SGD com implementação do Momentum
• Implementação do RMSprop
• Implementação de Adam
• Script de benchmarking para comparar os quatro algoritmos de otimização
• Um script para plotar resultados de benchmarking com o Matplotlib

E alguns recursos relacionados para que você saiba mais sobre o PyTorch e suas funções de otimização:

• Tutorial do PyTorch: Criando uma rede neural simples a partir do zero
• Programa de aprendizagem profunda em Python
• Curso intermediário de aprendizagem profunda em PyTorch
• Curso de aprendizagem profunda para imagens com PyTorch

Obrigado a você por ler!