Den euklidischen Abstand verstehen: Von der Theorie zur Praxis
Der euklidische Abstand, ein Konzept, das auf die antike griechische Mathematik zurückgeht, ist zu einem unverzichtbaren Werkzeug in der modernen Datenwissenschaft, dem maschinellen Lernen und der räumlichen Analyse geworden. Diese nach dem berühmten Euklid benannte Metrik bietet eine grundlegende Möglichkeit, den geradlinigen Abstand zwischen Punkten im Raum zu messen, egal ob in zwei oder mehr Dimensionen.
Was ist der euklidische Abstand?
Der euklidische Abstand ist der kürzeste Weg zwischen zwei Punkten im euklidischen Raum. Es ist der Abstand, den du mit einem Lineal messen würdest, erweitert auf eine beliebige Anzahl von Dimensionen. Dieses Konzept ist tief im Satz des Pythagoras verwurzelt, der besagt, dass in einem rechtwinkligen Dreieck das Quadrat der Länge der Hypotenuse gleich der Summe der Quadrate der beiden anderen Seiten ist.
"Philosophen lehren euklidischen Abstand." Bild von Dall-E
Die euklidische Abstandsformel
Lasst uns die Formel für den euklidischen Abstand für verschiedene Dimensionen aufschlüsseln:
2D Euklidischer Abstand
In einer zweidimensionalen Ebene ist der euklidische Abstand zwischen den Punkten A(x₁, y₁) und B(x₂, y₂) gegeben durch:
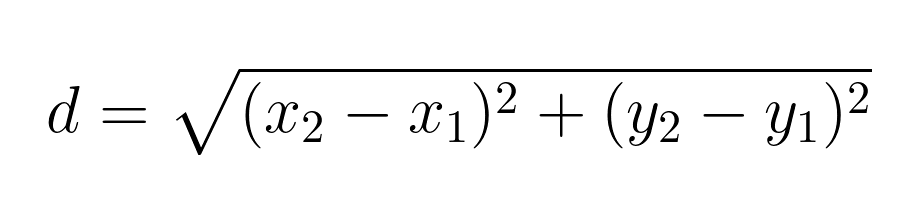
Berechnen wir zum Beispiel den Abstand zwischen den Punkten A(1, 2) und B(4, 6):
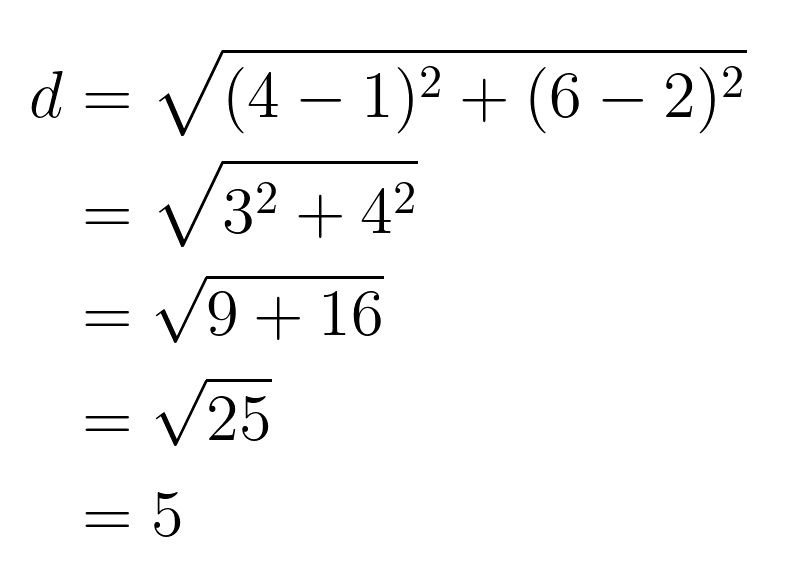
2D-Visualisierung der euklidischen Distanz
Um den euklidischen 2D-Abstand besser zu verstehen, wollen wir ihn visualisieren:
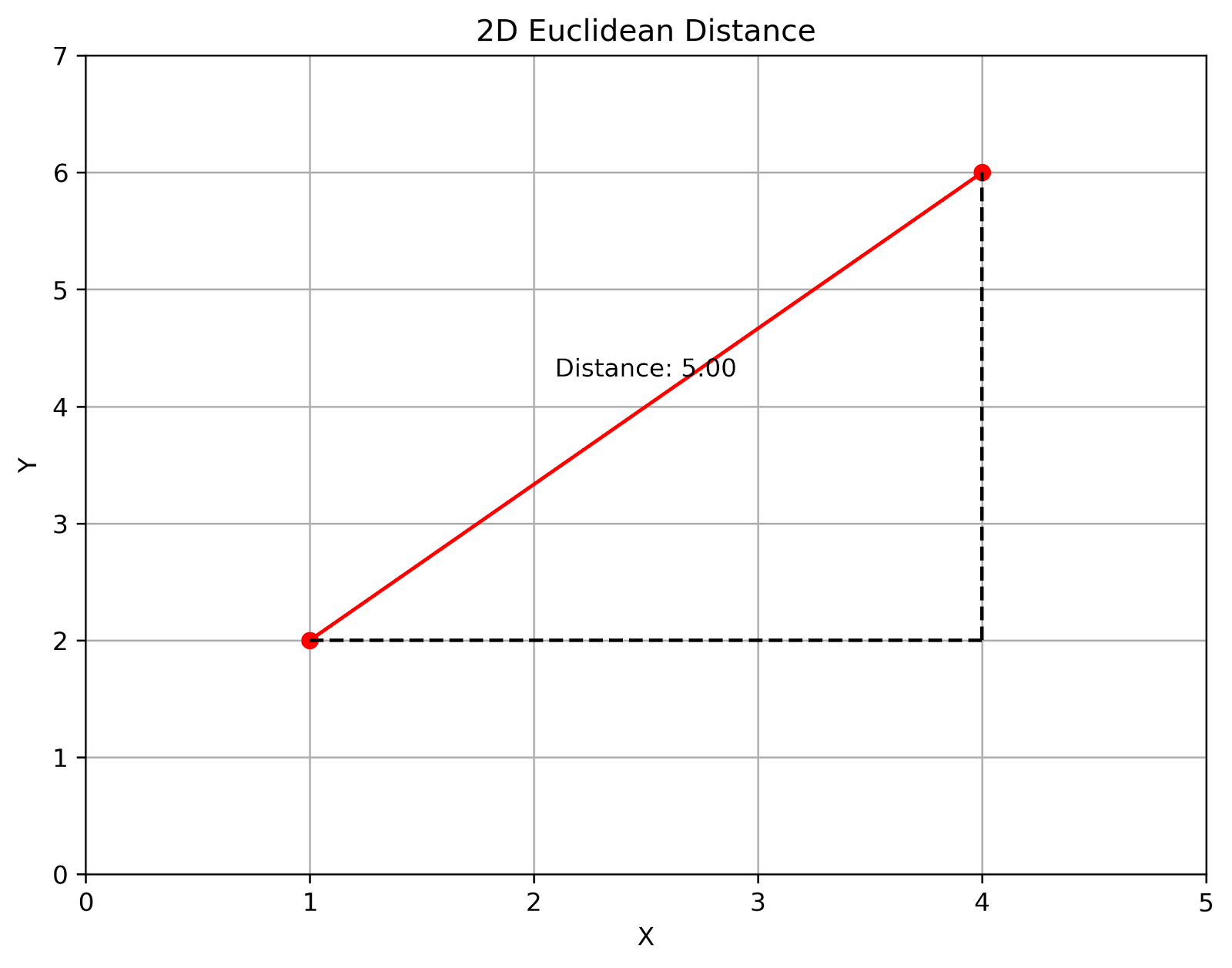
2D Euklidischer Abstand. Bild vom Autor
Diese Visualisierung zeigt den euklidischen Abstand zwischen zwei Punkten in einer 2D-Ebene. Die rote Linie stellt die direkte Entfernung dar, während die gestrichelten Linien ein rechtwinkliges Dreieck bilden, das den Satz des Pythagoras in Aktion zeigt.
Euklidischer 3D-Abstand
Auf drei Dimensionen ausgedehnt, ergibt sich für die Punkte A(x₁, y₁, z₁) und B(x₂, y₂, z₂) die folgende Formel:
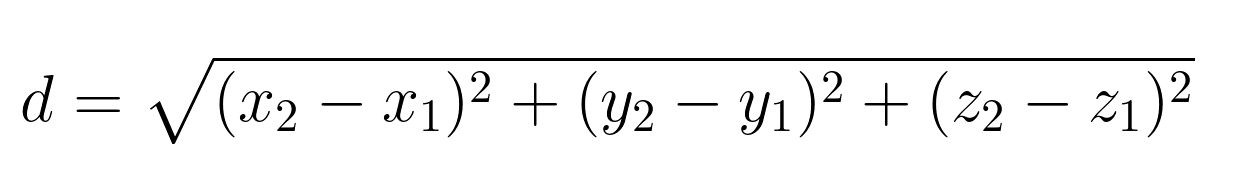
Visualisierung der euklidischen 3D-Distanz
Lass uns den euklidischen 3D-Abstand visualisieren:
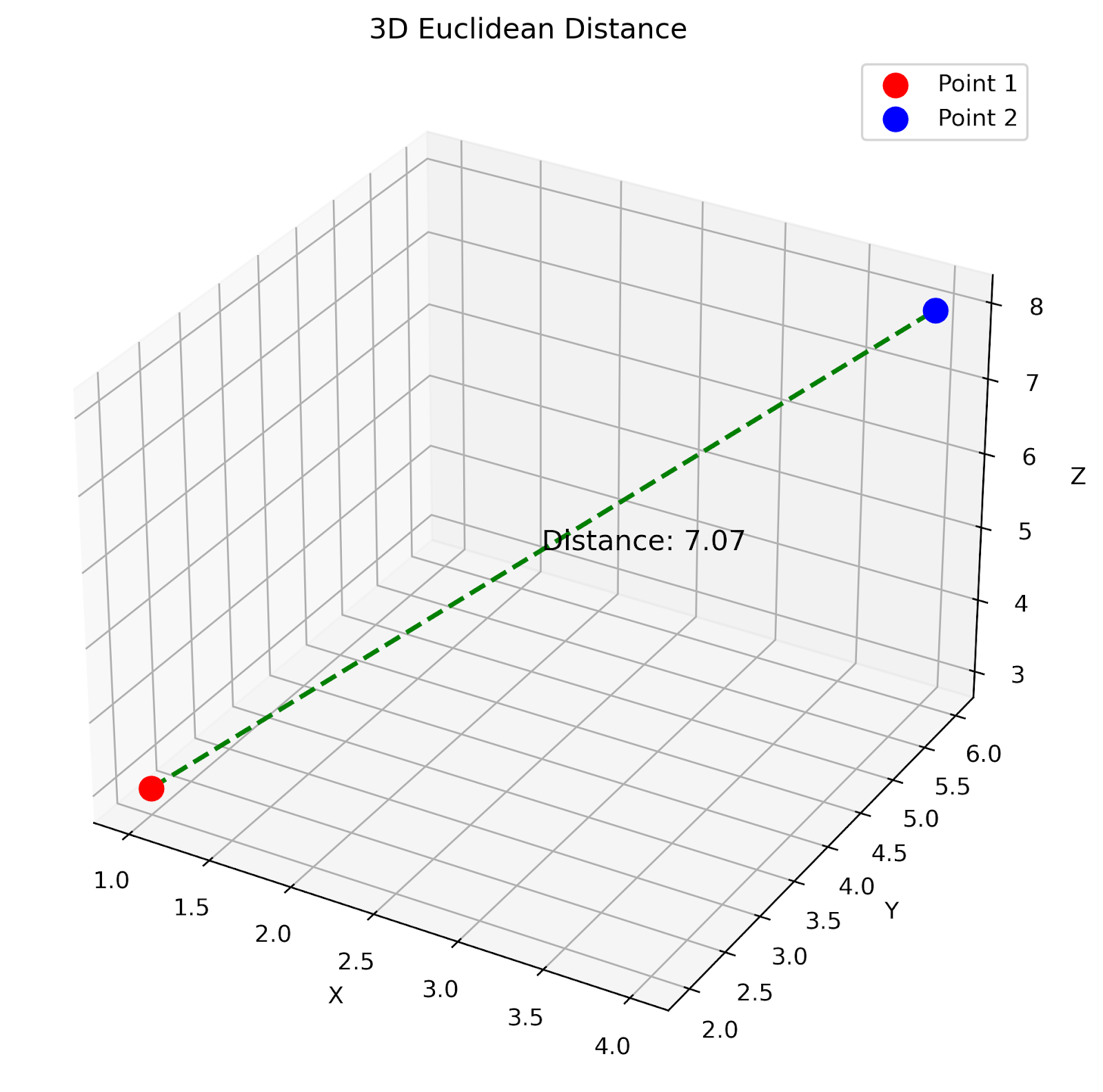
Euklidischer 3D-Abstand. Bild vom Autor
Diese 3D-Darstellung zeigt den euklidischen Abstand zwischen zwei Punkten im dreidimensionalen Raum. Die grün gestrichelte Linie stellt die direkte Entfernung zwischen den Punkten dar.
N-dimensionaler euklidischer Abstand
In einem Raum mit n Dimensionen ist der euklidische Abstand zwischen den Punkten A(a₁, a₂, ..., aₙ) und B(b₁, b₂, ..., bₙ):
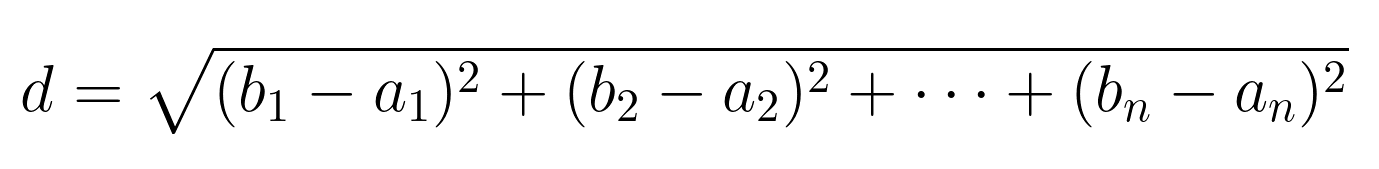
Das lässt sich mit der Summenschreibweise besser ausdrücken:
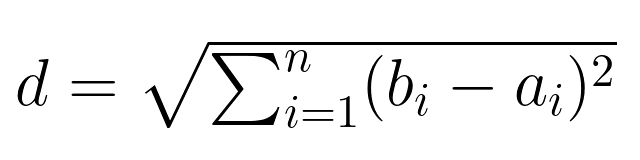
Beziehung zu Konzepten der linearen Algebra
Um den euklidischen Abstand zu verstehen, muss man nicht nur wissen, wie man den kürzesten Weg zwischen zwei Punkten misst. Es geht auch darum, diese Entfernungen durch die Linse der linearen Algebra zu sehen, einem Fachgebiet, das uns hilft, Probleme in Bezug auf Raum und Dimensionen mithilfe von Vektoren und ihren Eigenschaften zu beschreiben und zu lösen. Weitere Einblicke in dieses Thema erhältst du im Kurs Lineare Algebra für Datenwissenschaft in R, der diese Konzepte umfassend behandelt.
Euklidischer Abstand als Vektornorm
Der euklidische Abstand misst, wie weit zwei Punkte im Raum voneinander entfernt sind. Stell dir vor, du hast zwei Punkte, einen am Anfang eines Wanderweges und einen auf der Spitze eines Hügels. Den geradlinigen Weg, den du vom Start bis zum Gipfel zurücklegen würdest, kannst du dir als euklidische Distanz vorstellen. In der linearen Algebra ist das so, als würdest du die Länge eines Pfeils (oder Vektors) finden, der gerade vom Anfang des Weges (Punkt A) zur Spitze des Hügels (Punkt B) zeigt. Diese Länge wird als "Norm" des Vektors bezeichnet und ist nur ein schicker Ausdruck für die Länge des geradlinigen Pfades.
Punktprodukt und Kosinus des Winkels
Wenn es um Richtungen geht, hilft uns das Punktprodukt, den Winkel zwischen zwei beliebigen Pfeilen zu verstehen. Wenn du dich zum Beispiel an der Kreuzung zweier Straßen befindest, sagt dir das Punktprodukt, wie sehr die eine Straße auf die andere zeigt. Diese wird anhand der Längen der einzelnen Straßen (wie die Normen, über die wir gesprochen haben) und dem Winkel zwischen ihnen berechnet. Je näher dieser Wert bei 0 liegt, desto mehr nähern sich die Straßen einander an, da sie senkrecht zueinander stehen. Wenn du dies auf die Entfernung beziehst, hilft die Formel für das Punktprodukt dabei, die euklidische Entfernung in leichter zu handhabende Komponenten zu zerlegen, die zeigen, wie Richtungsänderungen die Gesamtentfernung beeinflussen.
Euklidischer Abstand und Vektorsubtraktion
Um den euklidischen Abstand zwischen zwei Punkten mithilfe von Vektoren zu bestimmen, subtrahierst du im Wesentlichen einen Punkt von einem anderen, um einen neuen Vektor zu erstellen. Dieser neue Vektor zeigt direkt von einem Punkt zum anderen und seine Länge ist der euklidische Abstand, an dem du interessiert bist. Das ist so, als würdest du den direkten Weg von deinem Haus zum nächsten Lebensmittelgeschäft auf einer Karte einzeichnen, indem du die Koordinaten subtrahierst; so erhältst du eine gerade Linie (oder einen Vektor), die den kürzesten Weg anzeigt, den du nehmen kannst.
Berechnung des euklidischen Abstands in Python und R
Wir werden uns die Implementierung der euklidischen Abstandsberechnung mit Python und R ansehen. Wir werden untersuchen, wie wir eigene Funktionen erstellen und integrierte Bibliotheken nutzen können, um die Effizienz zu steigern.
Python Beispiel
In Python können wir die Leistung von NumPy für effiziente Array-Operationen und SciPy für spezielle Abstandsberechnungen nutzen. Hier sehen wir, wie wir den euklidischen Abstand umsetzen können:
import numpy as np
from scipy.spatial.distance import euclidean
def euclidean_distance(point1, point2):
return np.sqrt(np.sum((np.array(point1) - np.array(point2))**2))
# 2D example
point_a = (1, 2)
point_b = (4, 6)
distance_2d = euclidean_distance(point_a, point_b)
print(f"2D Euclidean distance: {distance_2d:.2f}")
# 3D example
point_c = (1, 2, 3)
point_d = (4, 6, 8)
distance_3d = euclidean_distance(point_c, point_d)
print(f"3D Euclidean distance: {distance_3d:.2f}")
# Using SciPy for efficiency
distance_scipy = euclidean(point_c, point_d)
print(f"3D Euclidean distance (SciPy): {distance_scipy:.2f}")Wenn wir diesen Code ausführen, erwarten wir eine ähnliche Ausgabe wie diese:
2D Euclidean distance: 5.00
3D Euclidean distance: 7.07
3D Euclidean distance (SciPy): 7.07Die SciPy-Funktion ist im Allgemeinen schneller und optimierter, vor allem bei hochdimensionalen Daten, aber unsere benutzerdefinierte Funktion hilft, die zugrunde liegende Berechnung zu veranschaulichen.
Werde ein ML-Wissenschaftler
Werde ein ML-Wissenschaftler
Bilde dich in Python weiter, um ein/e Wissenschaftler/in für maschinelles Lernen zu werden.
