Bedingte Wahrscheinlichkeit: Ein genauer Blick

Stell dir vor, du entwickelst ein Spam-Erkennungssystem für E-Mails. Anfänglich kannst du eine E-Mail als verdächtig kennzeichnen, wenn sie bestimmte Schlüsselwörter enthält. Was aber, wenn du feststellst, dass diese E-Mail von einem vertrauenswürdigen Absender stammt? Oder was ist, wenn sie zu einer ungewöhnlichen Zeit gesendet wurde? Mit jeder neuen Information ändert sich die Wahrscheinlichkeit, dass es sich bei der E-Mail um Spam handelt. Diese dynamische Aktualisierung der Wahrscheinlichkeiten auf der Grundlage neuer Beweise ist das Herzstück der bedingten Wahrscheinlichkeit, ein Konzept, das viele moderne datenwissenschaftliche Anwendungen ermöglicht, von der E-Mail-Filterung bis zur Betrugserkennung. 

Für diejenigen, die sich zum ersten Mal mit Wahrscheinlichkeitskonzepten beschäftigen, ist der Spickzettel Einführung in die Wahrscheinlichkeitsregeln eine hilfreiche Referenz für die wichtigsten Prinzipien und Formeln. Der Kurs Einführung in die Statistik schafft eine solide Grundlage, indem er Wahrscheinlichkeitsverteilungen und ihre Eigenschaften erforscht, die die Basis für das Verständnis bilden, wie die bedingte Wahrscheinlichkeit in der Praxis funktioniert. Diese Ressourcen bieten einen strukturierten Weg zur Entwicklung solider Grundlagen in den Konzepten, die wir in diesem Artikel erforschen werden.

Was ist bedingte Wahrscheinlichkeit?

Die bedingte Wahrscheinlichkeit misst, wie wahrscheinlich es ist, dass ein Ereignis eintritt, wenn wir wissen, dass ein anderes Ereignis bereits stattgefunden hat. Wenn wir neue Informationen über ein Ereignis erhalten, passen wir unsere Wahrscheinlichkeitsberechnungen entsprechend an.

Um dieses Konzept zu verstehen, lass uns ein Beispiel mit Spielkarten untersuchen. Wenn du eine Karte aus einem Standarddeck ziehst, gibt es 52 mögliche Ergebnisse. Wenn du einen König ziehen willst, ist deine anfängliche Wahrscheinlichkeit 4/52 (etwa 7,7 %), da es vier Könige im Deck gibt. Aber was passiert, wenn dir jemand sagt, dass die Karte, die du gezogen hast, eine Bildkarte ist? Diese neue Information ändert alles - deine Wahrscheinlichkeit, einen König zu haben, ist jetzt viel höher, nämlich 4/12 (etwa 33,3 %), da es insgesamt nur zwölf Bildkarten gibt.

Diese Beziehung zwischen Wahrscheinlichkeiten hat eine genaue mathematische Definition:

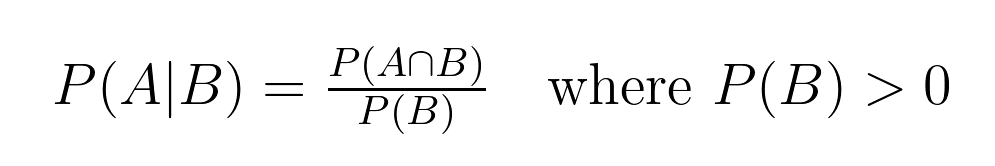
Diese Formel hilft uns, die bedingte Wahrscheinlichkeit zu berechnen, wobei:

• P(A|B) ist die Wahrscheinlichkeit, dass das Ereignis A eintritt, wenn das Ereignis B eingetreten ist. Dies wird als "die Wahrscheinlichkeit von A bei B" gelesen.
• P(A∩B) ist die gemeinsame Wahrscheinlichkeit, also die Wahrscheinlichkeit, dass die beiden Ereignisse A und B zusammen eintreten. Dies wird als "die Wahrscheinlichkeit, dass A B schneidet" gelesen.
• P(B) ist die Wahrscheinlichkeit, dass das Ereignis B eintritt.

In unserem Kartenbeispiel:

• Ereignis A ist "einen König ziehen"
• Ereignis B ist "eine Bildkarte ziehen".
• P(A|B) = 4/12 (Wahrscheinlichkeit, einen König zu bekommen, wenn wir eine Bildkarte haben)
• P(A∩B) = 4/52 (Wahrscheinlichkeit, einen König zu ziehen, der immer eine Bildkarte ist)
• P(B) = 12/52 (Wahrscheinlichkeit, eine beliebige Bildkarte zu ziehen)

Um besser zu verstehen, wie die bedingte Wahrscheinlichkeit in der Praxis funktioniert, können wir ein Baumdiagramm verwenden. Baumdiagramme sind besonders hilfreich, weil sie zeigen, wie jede neue Information unsere Wahrscheinlichkeiten verändert:

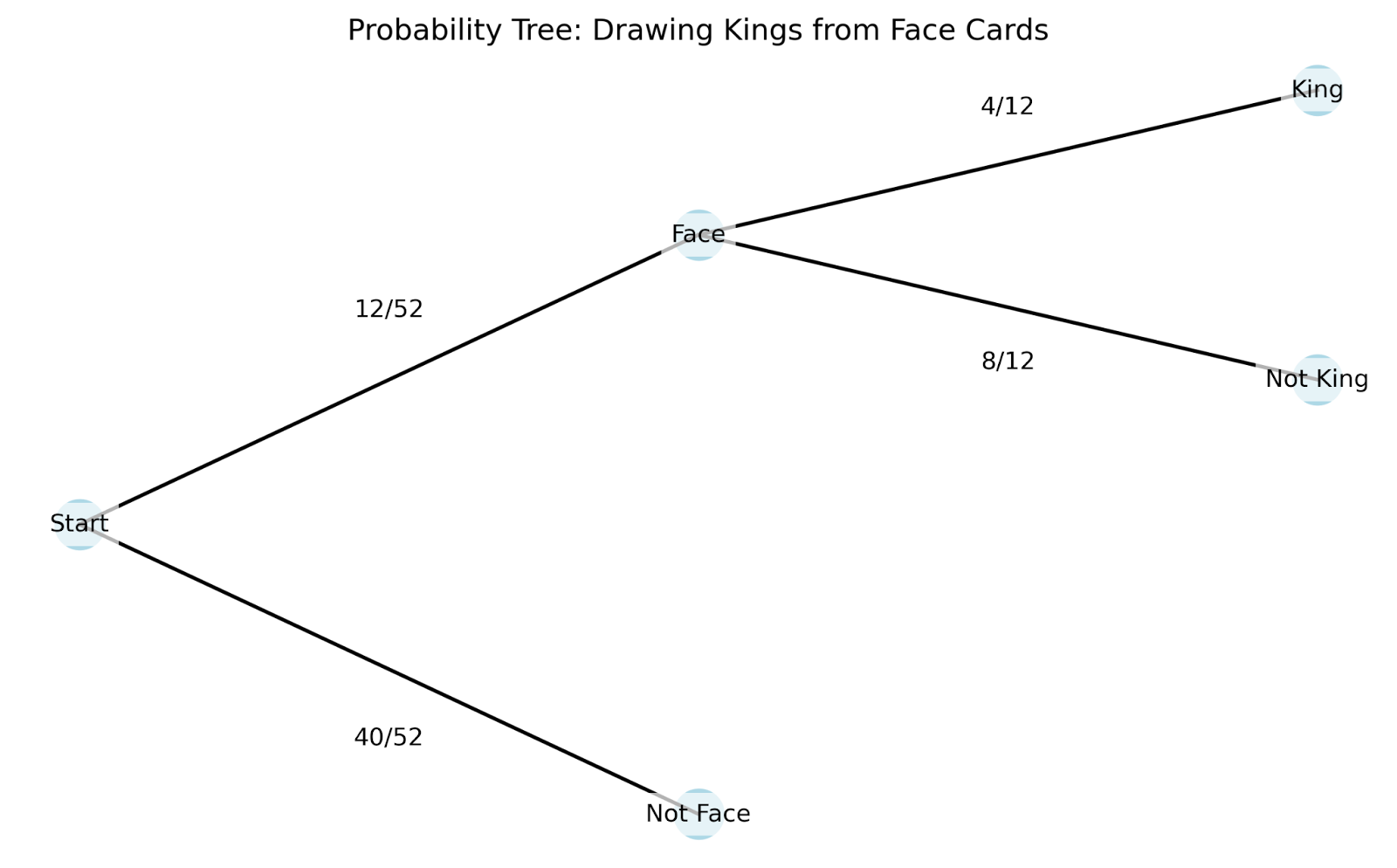
Schauen wir uns an, wie dieses Baumdiagramm funktioniert:

1. Wir beginnen bei der Wurzel (ganz links) mit allen 52 Karten.
2. Die ersten Zweige zeigen unsere erste Information - ist es eine Bildkarte oder nicht?
3. Wenn wir dem Gesichtskartenzweig folgen, teilt er sich aufgrund unserer zweiten Information wieder auf - ist es ein König?

Das Baumdiagramm hilft uns, verschiedene Schlüsselkonzepte der bedingten Wahrscheinlichkeit zu verstehen:

• Beispielraum: Das sind alle möglichen Ergebnisse in unserem Szenario. Der ursprüngliche Stichprobenraum beträgt 52 Karten, aber er wird auf 12 Karten "reduziert", sobald wir wissen, dass wir eine Bildkarte haben.
• Veranstaltungen: Das sind bestimmte Ergebnisse, an denen wir interessiert sind, wie "eine Bildkarte ziehen" oder "einen König ziehen". Die Äste in unserem Baum stehen für verschiedene Ereignisse.
• Gemeinsame Wahrscheinlichkeit: Das ist die Wahrscheinlichkeit, dass mehrere Ereignisse gleichzeitig eintreten. In unserem Baum können wir das herausfinden, indem wir die Wahrscheinlichkeiten entlang eines Pfades multiplizieren. Zum Beispiel ist die Wahrscheinlichkeit, einen König zu ziehen UND dass er eine Bildkarte ist, (12/52) × (4/12) = 4/52.
• Marginale (unbedingte) Wahrscheinlichkeit: Das ist die Wahrscheinlichkeit, dass ein Ereignis eintritt, ohne dass andere Informationen berücksichtigt werden. In unserem Beispiel ist das die anfängliche Wahrscheinlichkeit von 4/52, einen König zu ziehen, bevor wir etwas anderes über die Karte wissen.

Das Schöne an der bedingten Wahrscheinlichkeit ist, dass wir unsere Wahrscheinlichkeiten aktualisieren können, wenn wir neue Informationen erhalten. So wie wir unsere Wahrscheinlichkeit, einen König zu haben, von 7,7 % auf 33,3 % angepasst haben, als wir erfuhren, dass wir eine Bildkarte haben, gibt uns die bedingte Wahrscheinlichkeit eine formale Möglichkeit, Wahrscheinlichkeiten auf der Grundlage neuer Erkenntnisse neu zu berechnen.

Die Formel für die bedingte Wahrscheinlichkeit

Die mathematische Struktur der bedingten Wahrscheinlichkeit gibt uns Werkzeuge an die Hand, um komplexe Szenarien mit mehreren Ereignissen zu analysieren. Lass uns die wichtigsten Eigenschaften untersuchen.

Wichtige Eigenschaften der bedingten Wahrscheinlichkeit

Diese mathematischen Eigenschaften helfen uns, komplexe Probleme effizienter zu lösen:

1. Eigentum der Unabhängigkeit

Wenn zwei Ereignisse A und B unabhängig voneinander sind, wissen wir, dass das Eintreten des einen Ereignisses keinen Einfluss auf die Wahrscheinlichkeit des anderen Ereignisses hat. Mathematisch gesehen, ist das so: P(A|B) = P(A), was so viel heißt wie: "Die Wahrscheinlichkeit von A bei B ist gleich der Wahrscheinlichkeit von A."

Wenn wir zum Beispiel einen Würfel werfen und eine Münze werfen, ändert ein Kopf auf der Münze nichts an der Wahrscheinlichkeit, eine Sechs zu würfeln. Die Formel zeigt uns: P(Six|Heads) = P(Six) = 1/6

2. Komplementärregel

Für jedes Ereignis A unter der Bedingung B müssen die Wahrscheinlichkeiten von A und seinem Komplement A' (gelesen als "A prime") die Summe 1 ergeben. Mathematisch gesehen, ist das so: P(A|B) + P(A'|B) = 1, was sich wie folgt liest: "Die Wahrscheinlichkeit von A bei B plus die Wahrscheinlichkeit der Ergänzung von A bei B ist gleich 1."

In unserem früheren Kartenbeispiel: P(König|Kopfkarte) + P(Nicht-König|Kopfkarte) = 4/12 + 8/12 = 1

Die Multiplikationsregel und die Kettenregel

Die Multiplikationsregel verbindet gemeinsame Wahrscheinlichkeiten mit bedingten Wahrscheinlichkeiten: P(A ∩ B) = P(A|B) × P(B). Wir sagen: "Die Wahrscheinlichkeit, dass sich A mit B kreuzt, ist gleich der Wahrscheinlichkeit von A bei B mal der Wahrscheinlichkeit von B."

Das gilt auch für mehrere Ereignisse durch die Kettenregel. Für drei Ereignisse A, B und C: P(A ∩ B ∩ C) = P(A|B ∩ C) × P(B|C) × P(C). Das heißt: "Die Wahrscheinlichkeit, dass A den Schnittpunkt von B mit C schneidet, ist gleich der Wahrscheinlichkeit, dass A den Schnittpunkt von B mit C hat, mal der Wahrscheinlichkeit, dass B den Schnittpunkt von C hat, mal der Wahrscheinlichkeit von C."

Lass uns das anhand einer Kartenziehsequenz in Aktion sehen:

1. Ziehen eines Königs (K)
2. Von den verbleibenden Karten eine Königin (Q) ziehen
3. Von den verbleibenden Karten ein Ass (A) ziehen

P(K ∩ Q ∩ A) = P(A|K ∩ Q) × P(Q|K) × P(K) = (4/50) × (4/51) × (4/52)

Die Kettenregel ist beim maschinellen Lernen besonders wertvoll, vor allem in Bayes'schen Netzen, wo wir komplexe Abhängigkeiten zwischen mehreren Variablen modellieren müssen. Bei der Analyse von Daten stoßen wir oft auf Situationen, in denen die Ereignisse einer natürlichen Abfolge folgen, und die Kettenregel hilft uns, diese komplexen Szenarien in einfachere, handlichere Berechnungen zu zerlegen.

Beispiele zur Veranschaulichung bedingter Wahrscheinlichkeiten

Schauen wir uns zwei der häufigsten Beispiele an und überlegen wir, wie die bedingte Wahrscheinlichkeit in deiner Arbeit auftauchen könnte.

Klassische Beispiele

Diese beiden Beispiele sind sehr häufig und es lohnt sich, sie zu studieren, besonders wenn du ein Vorstellungsgespräch führst:

Würfle: Reduzierte Probenräume verstehen

Wenn wir einen Würfel werfen, beginnt unser Stichprobenraum mit sechs Möglichkeiten: {1, 2, 3, 4, 5, 6}. Wenn wir Teilinformationen über den Wurf erfahren, ändert das unsere Wahrscheinlichkeitsberechnungen auf eine bestimmte Weise. Lass uns sehen, wie:

Die anfängliche Wahrscheinlichkeit, eine 6 zu würfeln: P(6) = 1/6

Wenn wir erfahren, dass der Wurf gerade war, reduziert sich unser Stichprobenraum auf {2, 4, 6}: P(6 | even) = 1/3

Murmeln: Sequentielle Abhängigkeiten

Ein Beutel enthält 5 blaue Murmeln und 3 rote Murmeln. Wenn wir Murmeln ohne Ersatz ziehen, beeinflusst jede Ziehung die Wahrscheinlichkeiten der nachfolgenden Ziehungen.

Erste Ziehung - Wahrscheinlichkeit von Blau: P(blue₁) = 5/8

Zweite Ziehung, da die erste blau war: P(blue₂ | blue₁) = 4/7

Dieses Beispiel ergänzt unser früheres Kartenbeispiel, indem es die sequentiellen Abhängigkeiten hervorhebt.

Beispiele aus der realen Welt

Medizinische Tests: Bewertung der Testgenauigkeit

Medizinische Tests bieten eine perfekte Anwendung der bedingten Wahrscheinlichkeit bei der Bewertung der Testgenauigkeit. Für jeden diagnostischen Test müssen wir vier wichtige bedingte Wahrscheinlichkeiten kennen:

1. P(T+ | D+): Wahrscheinlichkeit eines positiven Tests, wenn der Patient die Krankheit hat (Sensitivität) 
2. P(T- | D-): Wahrscheinlichkeit eines negativen Tests, wenn der Patient die Krankheit nicht hat (Spezifität) 
3. P(T+ | D-): Wahrscheinlichkeit eines positiven Tests, wenn der Patient die Krankheit nicht hat (Falsch-Positiv-Rate) 
4. P(T- | D+): Wahrscheinlichkeit eines negativen Tests, wenn der Patient die Krankheit hat (falsch-negative Rate)

Bei der Bewertung der Leistung dieses Tests verwenden medizinische Fachkräfte diese bedingten Wahrscheinlichkeiten, um:

1. Vergleiche die Genauigkeit der Tests in verschiedenen Patientenpopulationen
2. Ermitteln, wann mehrere Tests erforderlich sind
3. Lege geeignete Schwellenwerte für positive/negative Ergebnisse fest

Wenn wir zum Beispiel 1000 Patienten testen und 100 positive Ergebnisse erhalten, können wir diese bedingten Wahrscheinlichkeiten verwenden, um abzuschätzen, wie viele davon echte positive Ergebnisse und wie viele falsche positive Ergebnisse sind. Diese Analyse hilft medizinischen Fachkräften, die Risiken einer fehlenden Diagnose gegen die Kosten und die Angst vor Fehlalarmen abzuwägen.

Finanzielle Risikobewertung

Wertpapierfirmen nutzen die bedingte Wahrscheinlichkeit, um Marktrisiken zu bewerten. Nehmen wir an, ein Portfoliomanager verfolgt die Marktvolatilität:

Die tägliche Marktvolatilität kann niedrig sein (L), Mittel (M), oder Hoch (H) sein.

Historische Daten zeigen: 

• P(H morgen | H heute) = 0,70 
• P(M morgen | H heute) = 0,25 
• P(L morgen | H heute) = 0,05

Diese Informationen helfen Managern:

• Portfoliostrukturen auf der Grundlage der aktuellen Marktbedingungen anpassen
• Risikogrenzen für automatisierte Handelssysteme festlegen
• Notfallpläne für Zeiten anhaltend hoher Volatilität entwickeln

Bedingte Wahrscheinlichkeit und Bayes' Theorem

Bei der Untersuchung der medizinischen Tests haben wir einen wichtigen Unterschied festgestellt: Die Wahrscheinlichkeit, eine Krankheit zu haben, wenn der Test positiv ist, unterscheidet sich von der Wahrscheinlichkeit, positiv zu testen, wenn die Krankheit vorhanden ist. Der Satz von Bayes bietet einen formalen Rahmen, um diese Beziehung zu steuern und ermöglicht es uns, unsere Wahrscheinlichkeitsschätzungen zu aktualisieren, wenn neue Erkenntnisse auftauchen.

Das Theorem von Bayes verstehen

Das Bayes'sche Theorem drückt die Beziehung zwischen zwei bedingten Wahrscheinlichkeiten aus: P(A|B) = [P(B|A) × P(A)] / P(B). Wir lesen diese Gleichung folgendermaßen: "Die Wahrscheinlichkeit von A bei B ist gleich der Wahrscheinlichkeit von B bei A mal der Wahrscheinlichkeit von A, geteilt durch die Wahrscheinlichkeit von B."

Jede Komponente spielt eine Rolle:

• P(A): Die Vorwahrscheinlichkeit - unsere anfängliche Überzeugung über A, bevor wir den Beweis B sehen
• P(B|A): Die Wahrscheinlichkeit - wie wahrscheinlich der Beweis B ist, wenn A wahr ist
• P(B): Die Gesamtwahrscheinlichkeit der Beobachtung von Beweisen B
• P(A|B): Die nachträgliche Wahrscheinlichkeit - unsere aktualisierte Überzeugung über A, nachdem wir den Beweis B gesehen haben

Sehen wir uns an, wie das in der Praxis mit unserem medizinischen Testszenario funktioniert, das wir nun erweitert haben, um die vollständige Bayes'sche Analyse zu zeigen.

Ein Beispiel für medizinische Tests

Stell dir eine Krankheit vor, die 2% der Bevölkerung betrifft. Ein neuer diagnostischer Test hat:

• 95% Sensitivität: P(positiver Test | hat Bedingung) = 0,95
• 90% Spezifität: P(negativer Test | keine Bedingung) = 0,90

Wenn ein Patient positiv getestet wird, wie sollten wir unsere Meinung über seinen Zustand aktualisieren?

Lass uns dieses Problem Schritt für Schritt lösen:

1. Vorherige Wahrscheinlichkeit (vor der Prüfung): P(Bedingung) = 0,02 (2% Bevölkerungsrate)
2. Wahrscheinlichkeit eines positiven Tests angesichts der Bedingung: P(positiv|Bedingung) = 0,95 (Testsensitivität)
3. Gesamtwahrscheinlichkeit für einen positiven Test: P(positiv) = P(positiv|Bedingung) × P(Bedingung) + P(positiv|keine Bedingung) × P(keine Bedingung) = 0,95 × 0,02 + 0,10 × 0,98 = 0,019 + 0,098 = 0,117
4. Nachfolgewahrscheinlichkeit (unter Verwendung des Satzes von Bayes): P(Bedingung|positiv) = [0,95 × 0,02] / 0,117 ≈ 0,162 oder 16,2%

Diese Analyse zeigt, dass selbst bei einem positiven Test die Wahrscheinlichkeit, an der Krankheit zu erkranken, nur etwa 16,2 % beträgt - viel höher als die anfänglichen 2 %, aber vielleicht niedriger, als es die Intuition vermuten ließe.

Die Macht der Bayes'schen Aktualisierung

Das Bayes'sche Theorem kommt zum Tragen, wenn wir mehrere Beweise erhalten. Die Posteriorwahrscheinlichkeit jeder Berechnung wird zur Priorwahrscheinlichkeit für die nächste Aktualisierung. Zum Beispiel, wenn unser Patient einen zweiten positiven Test bekommt:

1. Neue Priorität: P(Bedingung) = 0,162 (aus unserer ersten Berechnung)
2. Likelihood: P(positiv|Bedingung) = 0,95
3. Berechne den neuen posterioren...

Diese sequentielle Aktualisierung bietet einen mathematischen Rahmen, um neue Erkenntnisse in unsere Wahrscheinlichkeitsschätzungen einfließen zu lassen. Das Schöne an der Bayes'schen Schlussfolgerung ist, dass sie quantifizieren kann, wie sich unsere Überzeugungen ändern sollten, wenn wir neue Informationen sammeln, und dass sie eine formale Methode zur Aktualisierung von Wahrscheinlichkeiten im Lichte von Beweisen bietet.

Anwendungen in der Datenwissenschaft

Schauen wir uns an, wie sich die bedingte Wahrscheinlichkeit in der Datenwissenschaft zeigt. 

Prädiktive Modellierung

Der Naive Bayes-Klassifikator, eines der einfachsten und dennoch leistungsfähigsten Werkzeuge des maschinellen Lernens, wendet das Bayes-Theorem an, um Kategorien auf der Grundlage von Merkmalswahrscheinlichkeiten vorherzusagen. Bei der Klassifizierung von E-Mails als Spam oder Nicht-Spam berechnet der Algorithmus beispielsweise die bedingte Wahrscheinlichkeit, dass eine E-Mail aufgrund der darin enthaltenen Wörter Spam ist. Sie geht zwar von der "naiven" Annahme aus, dass die Merkmale unabhängig sind, aber diese Vereinfachung funktioniert in der Praxis oft erstaunlich gut.

Entscheidungsbäume verfolgen einen anderen Ansatz für die bedingte Wahrscheinlichkeit, indem sie die Daten auf der Grundlage von Merkmalswerten aufteilen, um bedingte Teilmengen zu erstellen. An jedem Knotenpunkt stellt der Baum Fragen wie "Wie hoch ist die Wahrscheinlichkeit, dass unsere Zielvariable diesen bestimmten Merkmalswert annimmt?" Diese Aufteilungen werden fortgesetzt, bis wir reine oder fast reine Teilmengen erreichen und so eine Karte mit bedingten Wahrscheinlichkeiten erstellen, die unsere Vorhersagen steuern.

Risikomanagement

Kreditscoring-Systeme verwenden bedingte Wahrscheinlichkeiten, um die Wahrscheinlichkeit eines Kreditausfalls bei verschiedenen Kundenmerkmalen zu bewerten. Eine Bank könnte zum Beispiel die Wahrscheinlichkeit eines Zahlungsausfalls in Abhängigkeit von der Höhe des Einkommens, der Kreditwürdigkeit und dem Beschäftigungsstatus berechnen. Diese Berechnungen werden anspruchsvoller, wenn sie mehrere abhängige Risiken berücksichtigen, z. B. wie sich die Wahrscheinlichkeit eines Hypothekenausfalls bei einer Rezession und steigenden Zinsen verändern könnte. Investitionsrisikomodelle verwenden bedingte Wahrscheinlichkeiten, um den Value at Risk (VaR) zu schätzen, indem sie die Wahrscheinlichkeit bestimmter Verlusthöhen unter den aktuellen Marktbedingungen berechnen. Portfoliomanager nutzen diese bedingten Wahrscheinlichkeiten, um die Vermögensallokation anzupassen und zu verstehen, wie sich das Risiko einer Anlage in Abhängigkeit von der Leistung anderer Anlagen im Portfolio verändern könnte.

Maschinelles Lernen

Bayes'sche Netze sind die direkteste Anwendung der bedingten Wahrscheinlichkeit im maschinellen Lernen. Sie modellieren Beziehungen zwischen Variablen als gerichteten Graphen, bei dem der Zustand jedes Knotens von seinen Eltern abhängt. Diese Netzwerke eignen sich hervorragend für Aufgaben wie die medizinische Diagnose, bei der die Wahrscheinlichkeit verschiedener Krankheiten von mehreren miteinander verbundenen Symptomen und Testergebnissen abhängt.

Probabilistische grafische Modelle nutzen bedingte Abhängigkeiten, um komplexe Beziehungen in Daten darzustellen, was sie für Aufgaben wie Bilderkennung und natürliche Sprachverarbeitung wertvoll macht. Auch Deep-Learning-Modelle, die nicht explizit probabilistisch sind, geben in ihren letzten Schichten bedingte Wahrscheinlichkeiten aus, wenn sie Klassifizierungen vornehmen. Die Softmax-Funktion, die häufig in neuronalen Netzen verwendet wird, wandelt die Rohwerte in bedingte Wahrscheinlichkeiten um, die uns die Wahrscheinlichkeit jeder möglichen Klasse angesichts der Eingabedaten angeben.

Häufige Fallstricke und Fehlinterpretationen

Bei der Arbeit mit bedingter Wahrscheinlichkeit gibt es drei Hauptfehler, die oft zu falschen Schlussfolgerungen führen.

• Der Umkehrschluss, auch bekannt als die Verwechslung des Umkehrschlusses, tritt auf, wenn wir P(A|B) mit P(B|A) verwechseln. Wir haben das in unserem Beispiel mit den medizinischen Tests gesehen - die Wahrscheinlichkeit, eine Krankheit zu haben, wenn der Test positiv ist, unterscheidet sich von der Wahrscheinlichkeit, positiv zu testen, wenn du die Krankheit hast.
• Eine Vernachlässigung der Basisrate liegt vor, wenn wir uns auf bedingte Wahrscheinlichkeiten konzentrieren und dabei die zugrunde liegende Wahrscheinlichkeit eines Ereignisses ignorieren. Wenn zum Beispiel eine seltene Krankheit nur 1 von 10.000 Menschen betrifft, kann selbst ein hochpräziser Test überwiegend falsch-positive Ergebnisse liefern, einfach weil die Krankheit so selten ist.
• Der dritte Fallstrick besteht darin, dass die Beweise bei der Aktualisierung der Wahrscheinlichkeiten falsch gewichtet werden. Die Menschen neigen dazu, aktuelle oder dramatische Beweise überzubewerten, während sie stabile Hintergrundinformationen unterbewerten. Beim Finanzhandel zum Beispiel können Anleger auf aktuelle Marktnachrichten überreagieren und dabei die langfristigen Marktwahrscheinlichkeiten ignorieren.

Fortgeschrittene Themen und weitere Überlegungen

Zum Schluss wollen wir uns noch ein paar kompliziertere Ideen ansehen, die auf dem aufbauen, was wir geübt haben.

Konditionierung auf Null-Wahrscheinlichkeitsereignisse

Wenn wir von diskreten zu kontinuierlichen Wahrscheinlichkeitsverteilungen übergehen, stoßen wir auf eine interessante Herausforderung: Bestimmte Punkte in einer kontinuierlichen Verteilung haben eine Wahrscheinlichkeit von Null. Nehmen wir an, wir messen die genaue Körpergröße einer Person - während wir sagen könnten, dass die Wahrscheinlichkeit, dass jemand zwischen 170 und 171 Zentimeter groß ist, sinnvoll ist, ist die Wahrscheinlichkeit, dass jemand genau 170,5432... Zentimeter groß ist, technisch gesehen null. Dennoch wollen wir uns oft auf solch präzise Messungen verlassen. Die reguläre bedingte Wahrscheinlichkeit bietet einen mathematischen Rahmen für den Umgang mit diesen Situationen und erweitert unsere grundlegenden Konzepte durch die Verwendung von Dichtefunktionen und Maßtheorie auf kontinuierliche Fälle. Mit dieser Erweiterung können wir Aussagen treffen wie "die Wahrscheinlichkeitsverteilung des Gewichts einer Person, wenn sie genau 170,5 Zentimeter groß ist".

Partielle bedingte Wahrscheinlichkeiten und Erweiterungen

Die Jeffrey-Konditionalisierung erweitert die traditionelle bedingte Wahrscheinlichkeit auf Situationen, in denen unsere neuen Beweise nicht sicher sind, sondern eine eigene Wahrscheinlichkeit haben. Anders als bei der Standardkonditionierung, bei der wir absolute Gewissheit über unsere neuen Informationen voraussetzen, erlaubt uns die Jeffrey-Regel, unsere Überzeugungen auf der Grundlage unsicherer Beweise zu aktualisieren. Das passt besser zu realen Szenarien, in denen neue Informationen oft mit einem gewissen Grad an Unsicherheit einhergehen. Anstatt sicher zu wissen, dass ein medizinischer Test positiv ist, können wir zum Beispiel erfahren, dass er mit einer Wahrscheinlichkeit von 80 % positiv ist. Die Jeffrey-Regel bietet eine formale Methode zur Aktualisierung von Wahrscheinlichkeiten in diesen differenzierteren Situationen.

Fazit

Die bedingte Wahrscheinlichkeit bietet einen mathematischen Rahmen, um unsere Überzeugungen zu aktualisieren, wenn neue Informationen auftauchen. In diesem Artikel haben wir gesehen, wie dieses Konzept in verschiedenen Bereichen Anwendung findet, von der medizinischen Diagnose bis hin zur finanziellen Risikobewertung. Die von uns erforschten Prinzipien helfen uns zu verstehen, wie sich die Wahrscheinlichkeit bei neuen Erkenntnissen ändert, und ermöglichen so fundiertere Entscheidungen in datenwissenschaftlichen Anwendungen. Dieses Verständnis ist besonders wertvoll, wenn du mit Klassifizierungsalgorithmen, Risikomodellen und maschinellen Lernsystemen arbeitest, bei denen die Wahrscheinlichkeiten ständig aktualisiert werden.

Wenn du dein Fachwissen über Wahrscheinlichkeit und statistische Schlussfolgerungen weiter ausbauen möchtest, können verschiedene Kurse dein Verständnis dieser Konzepte durch die Bayes'sche Brille verbessern. Unser Kurs Grundlagen der Bayes'schen Datenanalyse in R führt in die wichtigsten Prinzipien und ihre praktischen Anwendungen ein, während unser Kurs Bayes'sche Modellierung mit RJAGS zeigt, wie man diese Konzepte mit leistungsstarken statistischen Werkzeugen umsetzt. Für Python-Nutzer/innen bietet unser Kurs Bayesianische Datenanalyse in Python praktische Erfahrungen bei der Anwendung dieser Methoden auf reale Probleme. Jeder Kurs bietet dir die Möglichkeit, dein Wissen über Wahrscheinlichkeitsrechnung und ihre Anwendungen in der modernen Datenwissenschaft zu erweitern.