Eigendecomposition: Ein Leitfaden für Anfänger zur Matrixfaktorisierung

Operationen mit Matrizen bilden den Kern der Berechnungen im maschinellen Lernen, in der statistischen Analyse und im wissenschaftlichen Rechnen. Zum Beispiel erfordern viele Operationen in der Statistik die Inversion, Diagonalisierung und Potenzierung von Matrizen. Solche Operationen sind rechenintensiv, aber es gibt Methoden, um eine Matrix in eine kleinere Menge von Matrizen zu zerlegen und so die Effizienz der Berechnungen zu erhöhen. Diese Operationen werden allgemein als Matrixfaktorisierung bezeichnet und haben je nach Art der erhaltenen kleineren Matrizen bestimmte Namen. 

Die Eigenwertzerlegung ist eine Methode der Matrixfaktorisierung, bei der Eigenwerte und Eigenvektoren die Elemente dieser Matrizen bilden. Das Verständnis der Matrixeigenkomposition bietet Ingenieuren des maschinellen Lernens und der Datenwissenschaften eine mathematische Grundlage, um Methoden wie Dimensionsreduktion und Matrixapproximation zu verstehen. Nachdem du diesen Artikel gelesen hast, belege den Kurs Lineare Algebra für Datenwissenschaft in R, um mehr über die zentralen mathematischen Themen zu erfahren , die den Datenwissenschaften zugrunde liegen.

Was ist Eigendekomposition?

Die Eigendekomposition ist eine Methode zur Faktorisierung von Matrizen, bei der eine quadratische Matrix in drei multiplikative Matrizen faktorisiert (zerlegt) wird. Eine solche Faktorisierung wird Eigenwertzerlegung genannt, weil die Einträge der Matrizen Eigenwerte und Eigenvektoren der ursprünglichen quadratischen Matrix sind. Mathematisch gesehen kann eine quadratische Matrix A in drei Matrizen zerlegt werden, und zwar so, dass:

wobei P die Matrix der Eigenvektoren von Aist , Deine Diagonalmatrix ist, deren Nicht-Null-Elemente die geordneten Eigenwerte der Matrix sind, und ^P-1 die Inverse der Matrix ist P.

Die Mathematik hinter der Eigendekomposition

Ich werde anhand eines Beispiels die mathematischen Operationen demonstrieren, mit denen man die Eigenwertzerlegung einer quadratischen Matrix analytisch herleiten kann. Unsere Beispielmatrix ist die 2x2 Quadratmatrix A. Wenn du mit den Techniken zum Kombinieren von Matrizen nicht weiterkommst, solltest du unseren Kurs Lineare Algebra für Datenwissenschaft in R besuchen, damit du weißt, wie die Matrixmultiplikation funktioniert.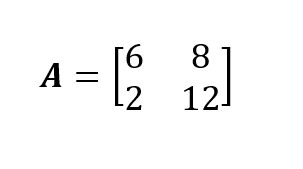

Um die Eigenwertzerlegung der Matrix Adurchzuführen , müssen wir die Eigenwerte und die entsprechenden Eigenvektoren dieser quadratischen Matrix ableiten. Wir können das charakteristische Polynom der Matrix verwenden, um die Eigenwerte und die Eigenvektoren dieser Matrix zu berechnen. Wenn du also mit diesem Teil nicht vertraut bist, lies Charakteristische Gleichung: Alles, was du für Data Science wissen musst zuerst. 

Aus der Definition eines charakteristischen Polynoms ergibt sich, dass wir

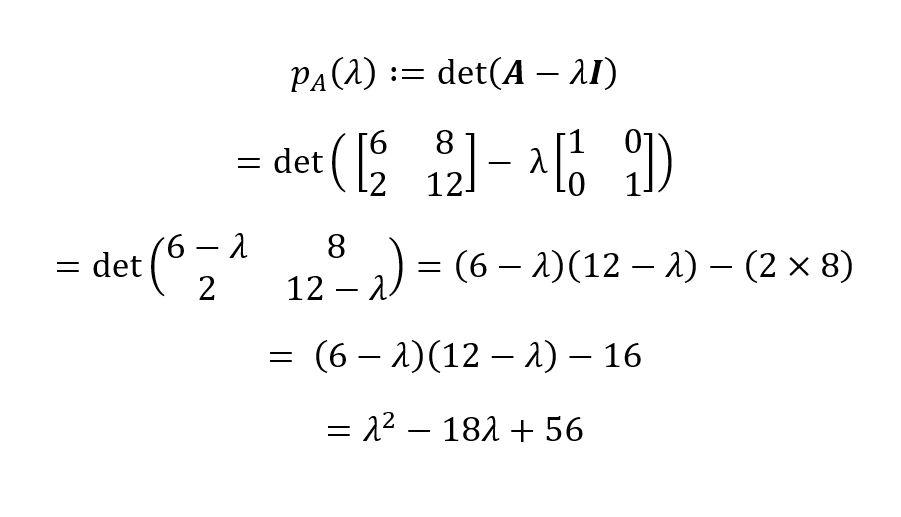
Das charakteristische Polynom für unsere Matrix A ist dann p_A(λ) = λ² - 18λ + 56. Wir können die Wurzeln dieses Polynoms finden, indem wir es mit Null gleichsetzen, um die Eigenwerte abzuleiten: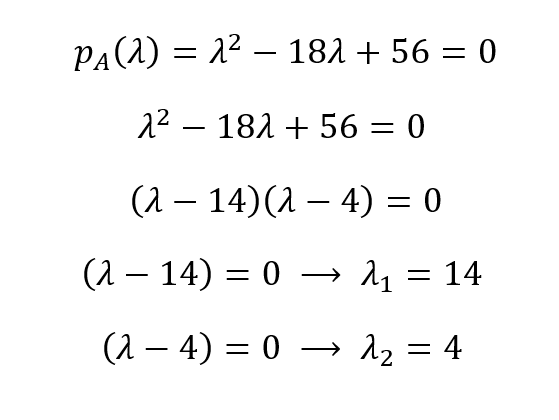 

Die Eigenwerte sind also λ₁ = 14 und λ₁ = 4. Aus den Eigenwerten können wir die Eigenvektoren einer Matrix mit (A - λI)X = 0 für jeden eindeutigen Eigenwert erhalten: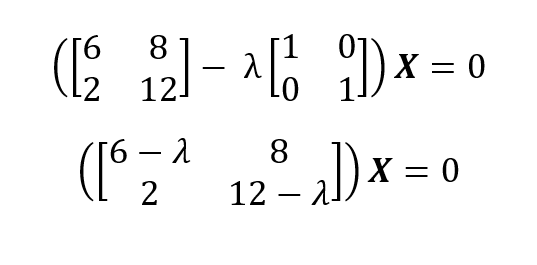

Für λ₁ = 14 setzen wir 14 ein und lösen das homogene Gleichungssystem:

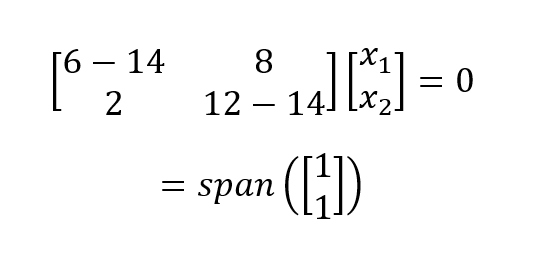
Das ergibt einen eindimensionalen (d.h. einen Basisvektor) Eigenraum. Wir führen das gleiche Verfahren für λ₁ = 4 und erhalten:

Nachdem wir nun die Eigenwerte und die Eigenvektoren der Matrix erhalten haben Aerhalten haben, können wir die Eigenwertzerlegung von A als:

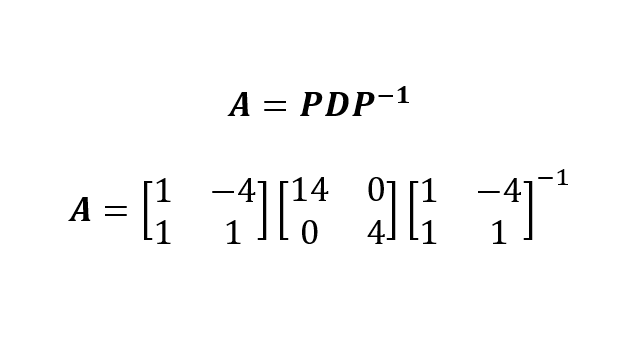
Dabei haben wir P konstruiert, indem wir die beiden Eigenvektoren zusammengefügt (d.h. nebeneinander gestellt) und die Eigenwerte (in absteigender Reihenfolge) auf die Diagonale der Matrix D gelegt haben. 

Natürlich können wir die Eigenwertzerlegung auch mit einem Computersystem und einer Programmiersprache wie Python oder R durchführen. Denke daran, dass Python und R normalisierte (auf der Skala 0-1) Eigenvektoren (d. h. eine orthonormale Basis) erzeugen können. Dies ist wichtig, wenn man versucht, die Matrix A aus PDP zu rekonstruieren^-1 zu rekonstruieren, um sie zu überprüfen.

Anwendungen der Eigendekomposition in der Datenwissenschaft

Die Eigendekomposition spielt eine wichtige Rolle beim maschinellen Lernen und in der Statistik. Beim maschinellen Lernen wird die Eigendifferenzierung für Dimensionsreduktionsverfahren wie die PCA verwendet. Bei der PCA suchen wir nach neuen Dimensionen (Richtungen) für die ursprünglichen hochdimensionalen Koordinaten, die ein Maximum an Informationen beibehalten. Die Eigenwertzerlegung der Matrix offenbart die Eigenwerte, und die Eigenvektoren mit den höchsten Eigenwerten enthalten mehr Informationen und werden daher als Hauptkomponenten der Daten bezeichnet.

Eigendekomposition in Python und R durchführen

Nachdem wir gelernt haben, wie man die Eigendifferenzierung mit Stift und Papier durchführt, können wir nun die Eigendifferenzierung mit einem Computer und einer Programmiersprache wie Python und R in wenigen Zeilen durchführen. Bedenke, dass die in Python und R berechneten Eigenvektoren normalisiert sind (im Vergleich zu symbolischen Programmiersprachen oder -paketen, wie SymPy in Python).

Eigendekomposition in Python

Um die eigendecomposition in Python durchzuführen, muss das Modul NumPy installiert und in die Umgebung importiert werden. Der folgende Code veranschaulicht, wie man in Python die Eigenschaftszerlegung für die quadratische, unsymmetrische Matrix A durchführt:

import numpy as np

A = np.array([[6,8], [2,12]]) 

eigVals, eigVecs = np.linalg.eig(A)

print(eigVals)
print(eigVecs)

[ 4. 14.]
[[-0.9701425  -0.70710678]
 [ 0.24253563 -0.70710678]]

 # Reconstruct the original matrix A
D = np.diag(eigVals)
A_reconstructed = eigVecs @ D @ np.linalg.inv(eigVecs)

print(A_reconstructed)

[[ 6.  8.]
 [ 2. 12.]]

Eigendekomposition in R

Die Eigendekomposition in R kann mit der eingebauten Funktion eigen() durchgeführt werden. Daher ist es nicht nötig, ein Paket für die Eigendekomposition von kleinen Matrizen zu installieren und zu importieren. Der folgende Code in R führt die Eigenwertzerlegung für die Matrix A durch (R sortiert die Eigenwerte in absteigender Reihenfolge, daher unterscheidet sich die Reihenfolge der Eigenvektoren von der Python NumPy-Ausgabe):

A <- matrix(c(6,8,2,12), 2,2, byrow = TRUE)

print(A)

eDecomp <- eigen(A)
eigValues <- eDecomp$values
eigVectors <- eDecomp$vectors

print(eigValues)
print(eigVectors)

[1] 14  4
           [,1]       [,2]
[1,] -0.7071068 -0.9701425
[2,] -0.7071068  0.2425356

A_Reconstructed <- eigVectors %*% diag(eigValues) %*% (solve(eigVectors))

print(A_Reconstructed)

Show in New Window
     [,1] [,2]
[1,]    6    8
[2,]    2   12

Eigendecomposition vs. Singulärwert-Zerlegung (SVD)

Die Eigenwertzerlegung und die Singulärwertzerlegung (SVD) sind zwei wichtige Methoden der Matrixfaktorisierung, die beim maschinellen Lernen und im wissenschaftlichen Rechnen eingesetzt werden. Obwohl beide Methoden eine Matrix in drei Matrizen faktorisieren, haben sie einige Unterschiede:

• Die Eigendekomposition ist nur auf quadratische Matrizen anwendbar, während die SVD sowohl auf quadratische als auch auf rechteckige Matrizen angewendet werden kann.
• Bei der SVD enthalten die resultierenden Matrizen singuläre Werte, bei der Eigenwertzerlegung dagegen Eigenwerte.
• Da SVD auch nicht-quadratische Matrizen aufnehmen kann, ist sie vielseitiger einsetzbar als die Eigenwertzerlegung.

Fazit

In diesem kurzen Artikel über lineare Algebra haben wir gelernt, was Eigenzerlegung ist, wie man sie mit Stift und Papier durchführt und wie man sie mit Python und R berechnet. Wir haben gelernt, wie Eigenzerlegung in Algorithmen des maschinellen Lernens wie der PCA verwendet wird. 

Wenn du dich stark dafür interessierst, Datenanalyst/in oder Datenwissenschaftler/in zu werden, empfehle ich dir dringend, unseren Kurs Lineare Algebra für Datenwissenschaft in R zu belegen, damit du eine starke Grundlage in angewandter Mathematik und Programmierung hast. Du kannst dich auch für unseren Lernpfad "Machine Learning Scientist in Python " anmelden, um über überwachtes, unüberwachtes und tiefes Lernen zu lernen.