Eigenvektoren und Eigenwerte: Wichtige Einblicke für Data Science

Eigenvektoren und Eigenwerte sind grundlegende Konzepte der linearen Algebra, die weitreichende Auswirkungen auf die Datenwissenschaft und das maschinelle Lernen haben. Diese mathematischen Einheiten bieten wertvolle Einblicke in das Verhalten von linearen Transformationen, die es uns ermöglichen, die zugrunde liegende Struktur von Daten zu verstehen, komplexe Datensätze mit einer großen Anzahl von Merkmalen zu vereinfachen und somit ihre Verarbeitung zu ermöglichen, um das gewünschte Ziel zu erreichen.

Wenn sich das für dich nach Dimensionalitätsreduktion anhört, hast du recht. Eigenvektoren und Eigenwerte sind die Grundlage vieler Verfahren zur Dimensionalitätsreduzierung, wie der Hauptkomponentenanalyse (PCA). Sie sind auch die Zahnräder für das spektrale Clustering, bei dem in einem ersten Schritt die Dimensionalität reduziert wird.

Um das Konzept der Eigenwelt zu verstehen, brauchst du ein gutes Verständnis der Konzepte der linearen Algebra, vor allem der Vektoren und Skalare, der linearen Transformation und der Determinanten. Wenn du mit diesen Konzepten noch nicht vertraut bist, kannst du unseren praktischen Kurs Lineare Algebra für Data Science in R besuchen. Wenn du Python verwendest, kannst du dieses SciPy-Tutorial zu Vektoren und Arrays durcharbeiten.

Was sind Eigenvektoren und Eigenwerte?

Beginnen wir mit der Tatsache, dass das "eigen" in Eigenvektoren und Eigenwerten tatsächlich eine Bedeutung hat und nicht der Name eines Typen ist, der sie erfunden hat. Eigen ist ein deutsches Wort, das in diesem Zusammenhang grob mit "das Charakteristische" oder "das Eigentliche" von etwas übersetzt werden kann.

Stell dir vor, wir unterziehen eine Gruppe von Vektoren einer linearen Transformation, wie Skalierung, Scherung oder Drehung. Manche Vektoren ändern ihre Richtung, und manche Vektoren tun das nicht. Die Vektoren, die ihre Richtung nicht ändern (oder sich genau in die entgegengesetzte Richtung drehen), nennen wir Eigenvektoren, da sie die "charakteristischen" Vektoren der erfolgten Transformation (oder der Matrix, die sie beschreiben) sind. Der Betrag, um den sie zufällig skaliert wurden, ist der Eigenwert. Das heißt, der Eigenwert ist der Skalierungsfaktor der Transformation.

Eigenvektoren und Eigenwerte verstehen

Um die Konzepte der beiden besser zu verstehen, wollen wir einen geometrischen Fall durchgehen und dann zu ihrer Anwendung in der Datenwissenschaft übergehen.

Geometrische Interpretation

Stell dir einen zweidimensionalen Raum vor, in dem wir drei Vektoren haben: einen blauen, der auf der x-Achse liegt, einen roten, der auf der y-Achse liegt, und einen grünen, der diagonal zwischen den beiden liegt. Jetzt wenden wir eine Skalierungstransformation entlang der y-Achse mit dem Faktor zwei an, wie in den folgenden Bildern zu sehen ist.

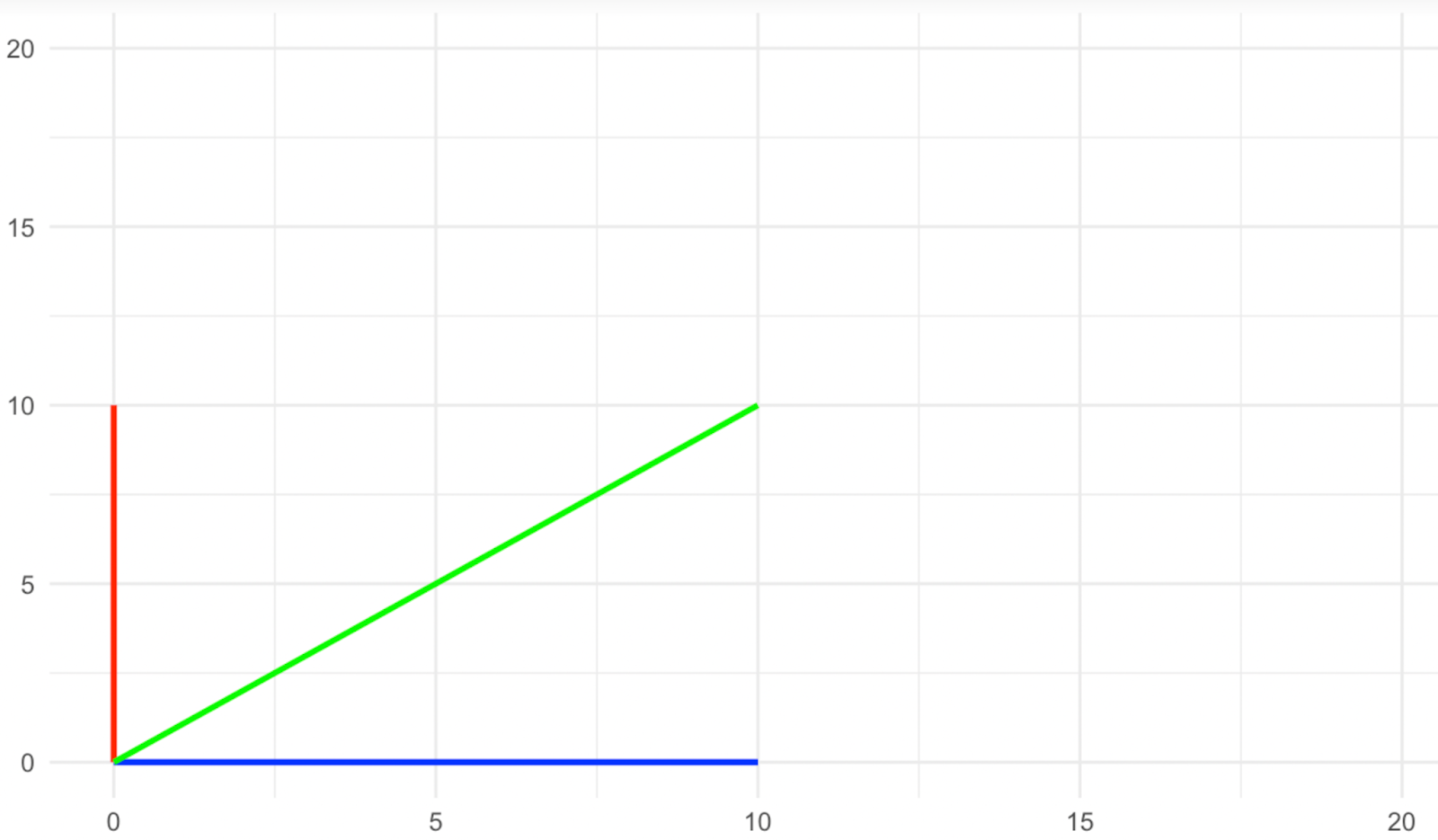
Vektoren vor dem Dehnen. Bild vom Autor

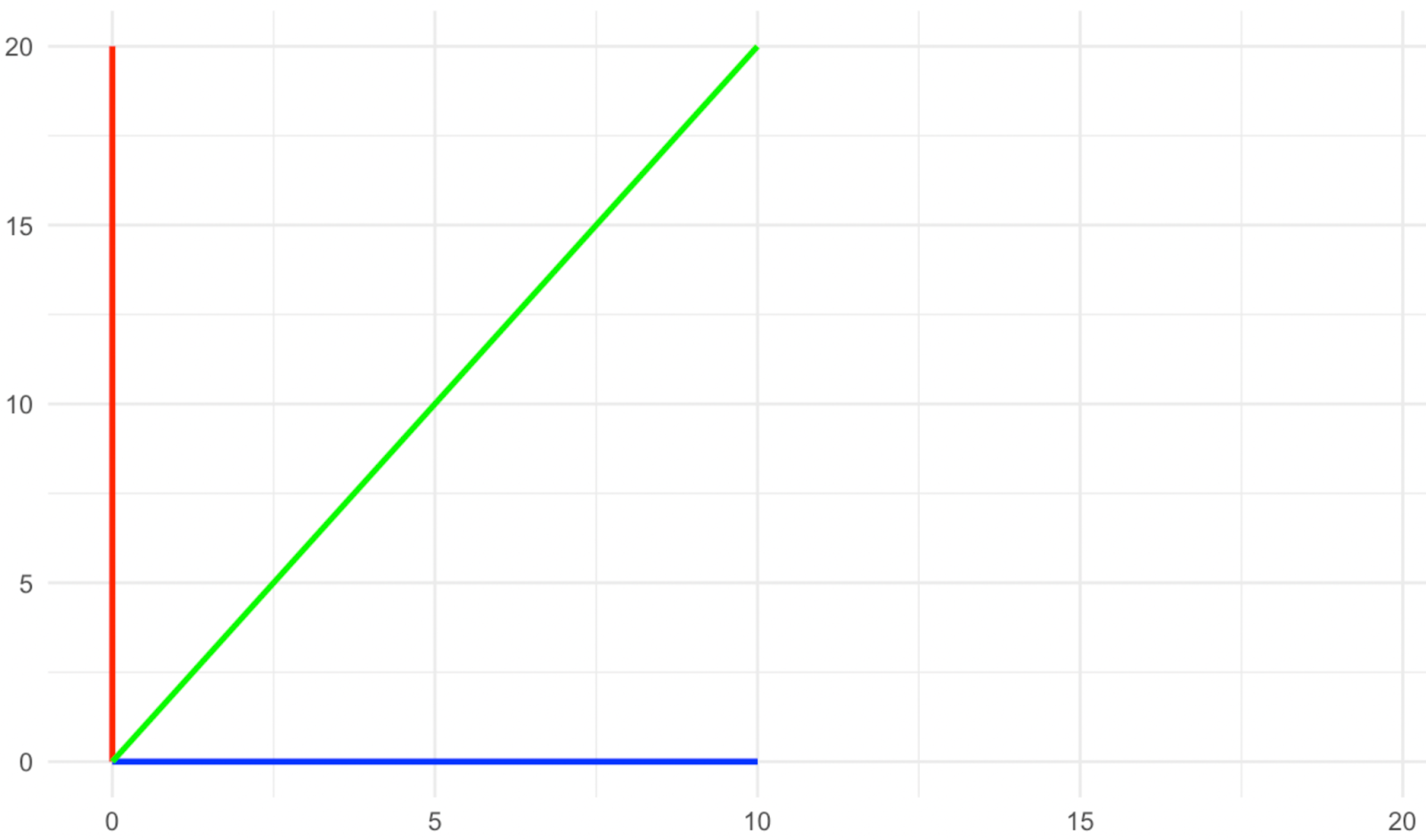
Vektoren nach dem Dehnen. Bild vom Autor

Was ist mit den Richtungsvektoren passiert? Die roten und blauen änderten ihre Richtung bei der Skalierung nicht, während die grüne ihre Richtung änderte, richtig? Deshalb nennen wir die roten und blauen Vektoren bei dieser Art von Transformation Eigenvektoren, da sie die charakteristischen Vektoren der Transformation sind.

Schau dir die Bilder oben noch einmal an und sieh dir an, was mit der Größe der Eigenvektoren (die roten und blauen) passiert ist. Der blaue Eigenvektor änderte seine Größe nicht, während der rote sich verdoppelte oder, wie man so schön sagt, um den Faktor zwei skaliert wurde. Der Betrag, um den jeder der Eigenvektoren durch die Transformation skaliert wurde, wird als Eigenwert bezeichnet. Daher ist der Eigenwert des blauen Eigenvektors hier 1 (betrachte dies als Multiplikation), während der Eigenwert des roten Eigenvektors 2 ist, da seine Größe verdoppelt wurde.

Eigenschaften von Eigenwerten

Betrachte die in den folgenden Bildern dargestellte Transformation und überlege dir zunächst, was die Eigenvektoren in diesem Fall sind. Wenn du sagst, dass es sich um die drei Vektoren Rot, Grün und Gelb handelt, hast du recht, denn sie zeigen nach der Transformation alle in die genau entgegengesetzte Richtung. Wir sehen, dass das Vorzeichen der Zahl (der Eigenwert) uns zusätzliche Informationen über die stattgefundene Transformation geben kann. Ein positiver Eigenwert zeigt an, dass die Transformation keine Drehung beinhaltet, während ein negativer Eigenwert anzeigt, dass die Transformation eine Drehung des Eigenvektors um seinen Ursprung beinhaltet.

Vektoren vor der Rotation. Bild vom Autor

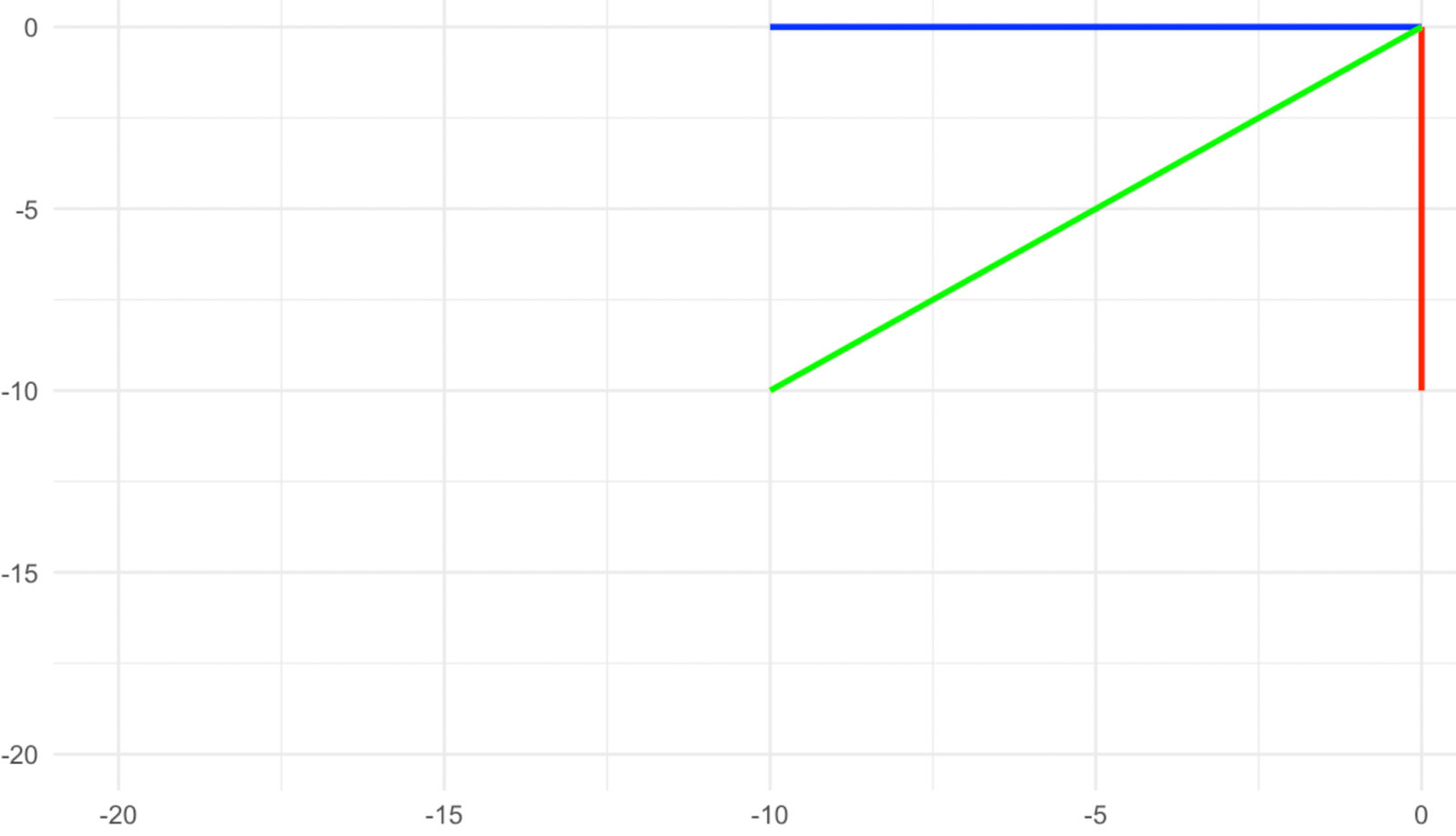
Vektoren nach der Rotation. Bild vom Autor

Wie lautet nun der Eigenwert jedes dieser Eigenvektoren? Die Tatsache, dass ihr Betrag gleich bleibt, bedeutet, dass der Eigenwert 1 ist, aber die Tatsache, dass sie sich auch gedreht haben, bedeutet, dass das Vorzeichen der 1 negativ sein muss. Daher ist der Eigenwert in diesem Fall -1.

In unserem Beispiel sind die Eigenwerte einfach (sie sind alle 1), aber Eigenwerte können jede beliebige Zahl sein, egal ob es sich um eine ganze Zahl handelt, wie 1 und 2, oder um einen rationalen (Bruch) wie ½ und 0,75. Sie können sogenannte irrationale Zahlen sein, wie der Wert von π. Eigenwerte können sogar komplexe Zahlen sein, wie z. B. a + bi, wobei "a" und "b" unabhängig voneinander reelle Zahlen sind und "i" eine imaginäre Einheit ist, wie die Quadratwurzel aus -1. Die komplexen Eigenwerte können auch Aufschluss über die Art der linearen Transformation geben, die stattgefunden hat, ob es sich um eine Drehung oder eine komplexere Transformation wie eine Oszillation handelt.

Wie man Eigenvektoren und Eigenwerte berechnet

Mit den Bibliotheken des Basispakets von R und den Python-Bibliotheken wie SciPy und NumPy lassen sich Eigenvektoren und Eigenwerte zwar leicht finden, aber die Gleichungen dahinter zu verstehen, ist äußerst wertvoll. In diesem Abschnitt werden wir die sogenannte charakteristische Gleichung besprechen, mit der die Eigenvektoren und Eigenwerte einer einfachen Matrix Schritt für Schritt berechnet werden. Dann werden wir andere mathematische Berechnungsmethoden für größere Matrizen (d.h. große Datensätze) erwähnen.

Charakteristische Gleichung

Wir können die Eigenvektoren und Eigenwerte mithilfe der so genannten charakteristischen Gleichung ermitteln. Mithilfe der charakteristischen Gleichung werden zuerst die Eigenwerte und dann die Eigenvektoren ermittelt. Sobald der Eigenwert bekannt ist, wird er verwendet, um den entsprechenden Eigenvektor zu berechnen, indem ein System linearer Gleichungen gelöst wird. 

Schritt 1: Beginne mit der Matrix-Transformationsgleichung

Für eine Matrix 𝐴 und einen Vektor 𝑣lautet die Grundgleichung für Eigenvektoren und Eigenwerte:

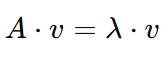
Das bedeutet, wenn die Matrix 𝐴 auf den Vektor 𝑣 wirkt , ist das Ergebnis eine skalierte Version von 𝑣. Hier:

• 𝐴 ist eine Matrix (ein quadratisches Gitter aus Zahlen).
• 𝑣 ist der Eigenvektor
• λ (lambda) ist der Eigenwert.

Denken wir daran, dass das Ziel darin besteht, beides zu finden λ (den Eigenwert) und 𝑣 (den Eigenvektor) zu finden.

Schritt 2: Stelle die Gleichung um

Um unser Ziel zu erreichen, müssen wir für λlösen . Deshalb werden wir die Gleichung zunächst umstellen, um sie leichter handhabbar zu machen, indem wir die rechte Seite auf die linke Seite mit umgekehrtem Vorzeichen verschieben:

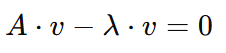
Jetzt können wir 𝑣 faktorisieren , aber da 𝐴 eine Matrix und 𝑣 ein Vektor ist , müssen wir 𝑣 mit einer sogenannten Identitätsmatrix ( I) multiplizieren . Eine Identitätsmatrix ist eine quadratische Matrix (mit der Größe nxn) mit 1en auf der Diagonalen und 0en anderswo. Aufgrund der Eigenschaft der Matrixmultiplikation verhält sich eine Identitätsmatrix wie die Zahl 1 für Matrizen. Nimm zum Beispiel diese Identitätsmatrix der Größe 3x3:

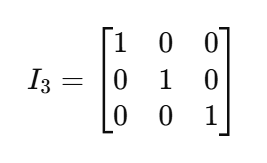
Zurück zu unserer Gleichung: Wenn wir den Faktor 𝑣und multiplizieren es mit Imultiplizieren, ergibt sich das folgende Ergebnis:

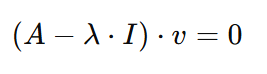
Schritt 3: Bestimmen Sie die Determinante

Um die Gleichung zu lösen, zu der wir gekommen sind, muss entweder der Eigenvektor 𝑣 Null sein, oder der Eigenvektor wäre gleich dem Wert 𝐴-λ⋅I. Und jetzt ist der richtige Zeitpunkt, um noch etwas über Eigenvektoren zu sagen: Sie können nicht gleich Null sein. Daher muss 𝐴-λ⋅I gleich Null sein. Da Lambda aber die Unbekannte ist, können wir die linke Seite der Gleichung gleich der rechten Seite machen, wenn wir die Determinante von 𝐴-λ⋅I nehmen. Daraus ergibt sich die folgende Gleichung:

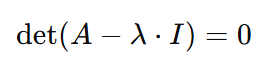
Hier sind wir bei der charakteristischen Gleichung angelangt. Das Lösen der charakteristischen Gleichung kann uns sowohl die Eigenwerte λ als auch den Eigenvektor 𝑣 liefern und wird in den weiteren Schritten gezeigt.

Schritt 4: Löse für Eigenwerte

Angenommen, wir haben die folgende Matrix 𝐴:

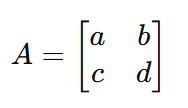
Durch Ersetzen von 𝐴 mit der tatsächlichen Matrix in der charakteristischen Gleichung, wird die Gleichung zu:

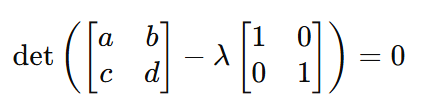
Und deshalb:

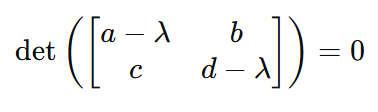
Und deshalb noch einmal:

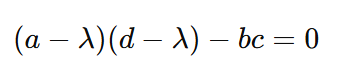
Aus dieser viel einfacheren Form der Gleichung können wir die Werte der Eigenwerte berechnen λ berechnen, indem wir einfach die Werte der Matrix einsetzen.

Schritt 5: Löse für Eigenvektoren 𝑣

Nachdem wir die Eigenwerte λerhalten haben , müssen wir nur noch die Eigenvektoren 𝑣 bestimmen . Wir können dies tun, indem wir zu der vorherigen Form der Gleichung zurückkehren:

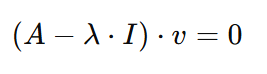
Wenn wir nun ersetzen 𝐴, λ, und I mit ihren Werten, können wir den Wert des Eigenvektors leicht berechnen 𝑣.

Numerische Berechnungsmethoden

Wie wir gesehen haben, hängt die Komplexität der Berechnung der Eigenvektoren und Eigenwerte stark von der Größe der Matrix ab. In unserem Beispiel haben wir eine einfache 2x2 𝐴 Matrix verwendet. Aber wir können die Eigenvektoren und Eigenwerte auf diese Weise praktisch nicht finden, wenn die Matrizen viel größer werden, z. B. wenn sie Hunderte oder Tausende von Zeilen und Spalten haben. In diesem Fall verwenden wir Programmiersprachen wie Python und R, die numerische Berechnungsmethoden im Gegensatz zu symbolischen Methoden verwenden. Einige der verwendeten Techniken sind:

1. QR-Algorithmus: Dies ist eine gängige Methode zur Ermittlung von Eigenwerten. Dabei wird eine Reihe von Matrixfaktorisierungen(QR-Faktorisierungen) durchgeführt, um iterativ zu den Eigenwerten zu konvergieren.
2. Cholesky- oder LU-Zerlegung: Für bestimmte Arten von Matrizen (z. B. symmetrische oder positiv definite Matrizen) können spezielle Methoden wie die Cholesky- oder LU-Zerlegung verwendet werden, um eine effizientere Berechnung zu ermöglichen.
3. Ausgleichen und Skalieren: Um die numerische Stabilität zu verbessern, skalieren und balancieren R und Python häufig Matrizen, bevor sie Berechnungen durchführen.

Überlegungen zu Data Science und maschinellem Lernen

Eigenvektoren und Eigenwerte sind für viele Anwendungen wichtig, unter anderem für die folgenden:

• Bildbearbeitung: Sie werden bei der Gesichtserkennung und Bildklassifizierung eingesetzt.
• Natürliche Sprachverarbeitung (NLP): Eigenvektoren und Eigenwerte werden bei der Themenmodellierung und bei der Worteinbettung verwendet.
• Empfehlungssysteme: Wie bei der kollaborativen und inhaltsbasierten Filterung, wo die Dimensionalitätsreduktion die Genauigkeit der Empfehlungssysteme verbessern kann.
• Spektrales Clustering: Eigenvektoren und Eigenwerte sind auch eine grundlegende Komponente des spektralen Clustering, einer Methode, bei der Datenpunkte anhand ihrer Verbindungen in einem Graphen gruppiert werden, wobei Informationen aus der Struktur der Daten und nicht nur der Abstand verwendet werden.
• Hauptkomponentenanalyse: Die PCA ist eine Technik zur Dimensionalitätsreduktion, die beim maschinellen Lernen üblich ist. Mit der PCA findest du die Eigenvektoren der standardisierten Kovarianzmatrix und sortierst sie nach Eigenwert. 

Wir haben gesagt, dass die Eigenwerte jede reelle oder komplexe Zahl sein können. Das bedeutet, dass der Eigenwert gleich Null sein kann, aber auch, dass wir mehrere Eigenwerte in der analysierten Matrix haben können, die gleich sind. Diese beiden Fälle werden als zwei Fehler betrachtet, die bei jeder Eigenanalyse auftreten können. Schauen wir uns beide an.

Null-Eigenwertproblem

Ein Null-Eigenwert ist ein Problem, weil er bedeutet, dass die Transformation des entsprechenden Eigenvektors zu einem Nullvektor geführt hat, den man sich als einen einzelnen Punkt im Raum ohne Größe vorstellen kann und der daher keine Varianz im Datensatz erklärt. Das Problem kann mit Regularisierungstechniken wie der Ridge Regression (Tikhonov-Regularisierung) oder mit der Entfernung kollinearer Merkmale (auch bekannt als Dimensionalitätsreduktion) gelöst werden, was natürlich in einem PCA-Algorithmus geschieht. Daher ist der Null-Eigenwert kein Problem für die PCA, und tatsächlich kann die PCA eine Lösung für dieses Problem sein. Bei anderen Algorithmen des maschinellen Lernens, die das Lösen linearer Systeme beinhalten, wie z. B. lineare, Ridge- und Lasso-Regressionen, sollte das Null-Eigenwert-Problem jedoch vorher gelöst werden.

Entartete Eigenwerte

Wenn mehrere Eigenwerte denselben Wert haben, werden sie als Entartungen bezeichnet und stellen in der Datenwissenschaft ein Problem dar, insbesondere aus praktischer Sicht bei der PCA und dem spektralen Clustering. Wenn bei der PCA mehrere Eigenvektoren identische Eigenwerte haben, bedeutet dies, dass diese Eigenvektoren den gleichen Anteil an der Varianz des Datensatzes erfassen, sodass die Auswahl von k Hauptkomponenten problematisch wird. Beim spektralen Clustering, bei dem Eigenwerte der Ähnlichkeitsmatrix verwendet werden, um Datenpunkte zu gruppieren, können entartete Eigenwerte darauf hinweisen, dass die Datenpunkte in mehreren Dimensionen gleich ähnlich sind, was es schwierig macht, zu bestimmen, welche Dimensionen oder Eigenvektoren zur Trennung der Cluster verwendet werden sollten.

Eigenvektoren, Eigenwerte und Eigendekomposition

Eine Diskussion über Eigenvektoren und Eigenwerte wäre unvollständig, wenn man nicht auch über die Eigenwertzerlegung sprechen würde. Die Eigenwertzerlegung ist der Prozess der Zerlegung einer quadratischen Matrix A in ihre Eigenvektoren und Eigenwerte. Für eine Matrix, die zerlegt werden kann, lässt sie sich wie folgt ausdrücken:

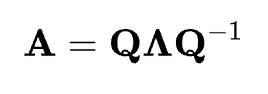
Die Eigenwertzerlegung besagt, dass die Matrix A als das Produkt aus ihrer Eigenvektor-Matrix Q, einer Diagonalmatrix Λ ihrer Eigenwerte und der Inversen der Eigenvektor-Matrix ^Q-1dargestellt werden kann. Wenn diese Matrizen bei der Matrixmultiplikation miteinander multipliziert werden, wird die ursprüngliche Matrix A rekonstruiert. Die Eigendekomposition ist wichtig, weil sie eine Möglichkeit bietet, komplexe lineare Transformationen zu verstehen und zu vereinfachen, was Einblicke in das Systemverhalten ermöglicht. 

Fazit

In diesem Artikel haben wir gesehen, was Eigenvektoren und Eigenwerte sind und wie wichtig sie für Data Science und maschinelles Lernen sind. Wir haben auch besprochen, wie sie mathematisch berechnet werden und welche Fehler beim Versuch, Eigenvektoren und Eigenwerte zu finden, auftreten können.

Neben dem Kurs Lineare Algebra in R und dem SciPy-Tutorial zu Vektoren und Arrays kannst du dich in unserem Karrierepfad Machine Learning Scientist with Python zum Experten für überwachtes und unüberwachtes Lernen und natürlich auch für Dimensionalitätsreduktion entwickeln, wenn du dich ernsthaft mit Eigenvektoren und Eigenwerten und ihren Anwendungen im maschinellen Lernen beschäftigst.