Eigendecomposition: Um guia para iniciantes sobre fatoração de matrizes

As operações em matrizes constituem o núcleo dos cálculos em aprendizado de máquina, análise estatística e computação científica. Por exemplo, muitas operações em estatística exigem inversão, diagonalização e exponenciação de matrizes. Essas operações são computacionalmente caras, mas há métodos para dividir uma matriz em um conjunto menor de matrizes e, assim, aumentar a eficiência da computação. Essas operações são geralmente chamadas de fatoração de matriz e, dependendo da natureza das matrizes menores obtidas, elas têm nomes específicos. 

A eigendecomposição é um método de fatoração de matrizes em que os valores e vetores próprios constituem os elementos dessas matrizes. A compreensão da eigendecomposição de matrizes fornece aos engenheiros de aprendizado de máquina e de ciência de dados uma base matemática para entender métodos como a redução de dimensão e a aproximação de matrizes. Depois que você ler este artigo, faça o curso Linear Algebra for Data Science in R para aprender sobre os tópicos matemáticos centrais que sustentam a ciência de dados.

O que é Eigendecomposition?

Eigendecomposition é um método de fatoração de matriz no qual uma matriz quadrada é fatorada (decomposta) em três matrizes multiplicativas. Essa fatoração é chamada de eigendecomposição porque as entradas das matrizes são valores e vetores próprios da matriz quadrada original. Matematicamente, uma matriz quadrada A pode ser dividida em três matrizes, de modo que:

em que P é a matriz dos vetores próprios de A, Dé uma matriz diagonal cujos elementos não nulos são os valores próprios ordenados da matriz, e ^P-1 é o inverso da matriz P.

A matemática por trás da Eigendecomposition

Demonstrarei, por meio de um exemplo, as operações matemáticas para derivar analiticamente a eigendecomposição de uma matriz quadrada. Nossa matriz de exemplo é a matriz quadrada 2x2 A. Se você tiver dúvidas sobre as técnicas de combinação de matrizes, faça nosso curso Linear Algebra for Data Science in R para se sentir confortável com o funcionamento da multiplicação de matrizes.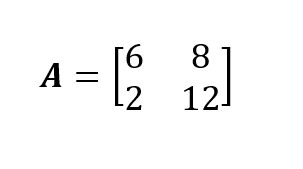

Para realizar a decomposição de eigend na matriz A, precisamos derivar os valores próprios e os vetores próprios correspondentes dessa matriz quadrada. Podemos usar o polinômio característico da matriz para calcular os valores próprios e os vetores próprios dessa matriz. Portanto, se você não estiver familiarizado com essa parte, leia Characteristic Equation: Tudo o que você precisa saber para a ciência de dados primeiro. 

Agora, com base na definição de um polinômio característico, temos:

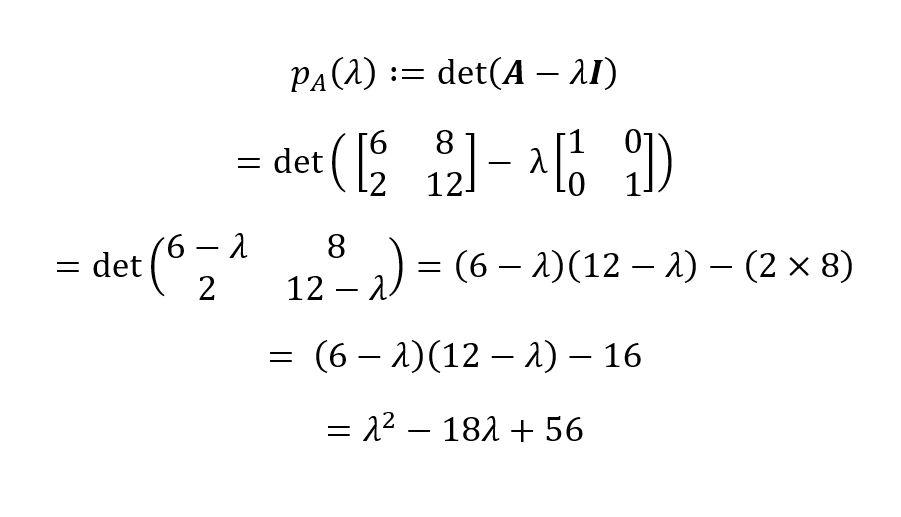
O polinômio característico da nossa matriz A é, então, p_A(λ) = λ² - 18λ + 56. Podemos encontrar as raízes desse polinômio igualando-o a zero para derivar os valores próprios: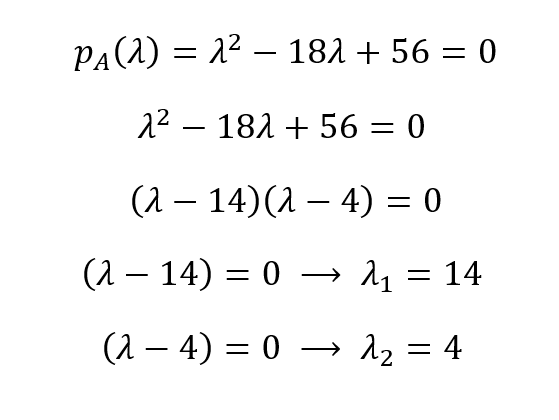 

Portanto, os valores próprios são λ₁ = 14 e λ₁ = 4. A partir dos valores próprios, podemos obter os vetores próprios de uma matriz usando (A - λI)X = 0 para cada valor próprio exclusivo: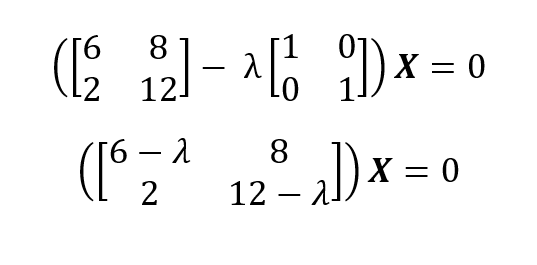

Para λ₁ = 14 inserimos 14 e resolvemos o sistema homogêneo de equações:

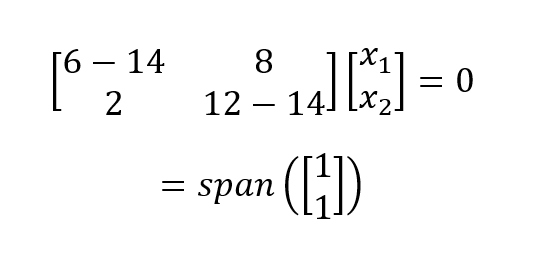
O que resulta em um eigenspace unidimensional (ou seja, um vetor de base). Realizamos o mesmo processo para λ₁ = 4 e obtemos:

Agora que obtivemos os valores próprios e os vetores próprios da matriz Apodemos escrever a decomposição de autovalores de A como:

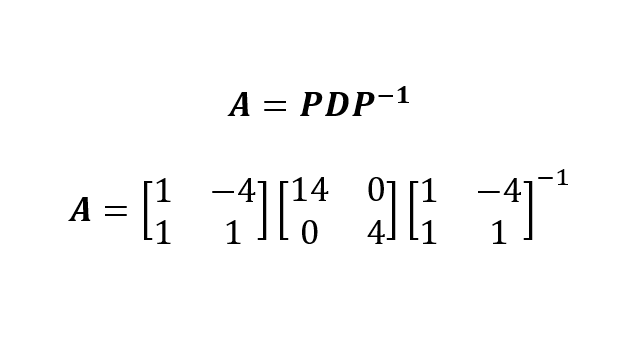
Na qual construímos P ao agrupar os dois vetores próprios (ou seja, colocá-los lado a lado) e colocamos os valores próprios (em ordem decrescente) na diagonal da matriz D. 

É claro que podemos realizar a decomposição de eigend com um sistema de computador e uma linguagem de programação como Python ou R. Lembre-se de que Python e R podem produzir vetores próprios normalizados (na escala 0-1) (ou seja, base ortonormal). É importante observar isso quando você tenta reconstruir a matriz A a partir do PDP^-1 para fins de verificação.

Aplicações da Eigendecomposição na ciência de dados

A eigendecomposição desempenha um papel importante no aprendizado de máquina e na estatística. No aprendizado de máquina, a eigendecomposição é usada para métodos de redução de dimensão, como o PCA. Na PCA, procuramos novas dimensões (direções) para as coordenadas originais de alta dimensão que retêm o máximo de informações. A decomposição da matriz revela os valores próprios, e os vetores próprios com os valores próprios mais altos retêm mais informações e, portanto, são designados como componentes principais dos dados.

Execução de Eigendecomposition em Python e R

Depois de aprender a fazer a eigendecomposição com caneta e papel, agora podemos fazer a eigendecomposição usando um computador e uma linguagem de programação, como Python e R, em poucas linhas. Lembre-se de que os vetores próprios calculados no Python e no R são normalizados (em comparação com as linguagens ou pacotes de programação simbólica, como o SymPy no Python).

Eigendecomposição em Python

Para realizar a eigendecomposição em Python, o módulo NumPy precisa ser instalado e importado para o ambiente. O código a seguir ilustra como executar a eigendecomposição em Python para a matriz quadrada não simétrica A:

import numpy as np

A = np.array([[6,8], [2,12]]) 

eigVals, eigVecs = np.linalg.eig(A)

print(eigVals)
print(eigVecs)

[ 4. 14.]
[[-0.9701425  -0.70710678]
 [ 0.24253563 -0.70710678]]

 # Reconstruct the original matrix A
D = np.diag(eigVals)
A_reconstructed = eigVecs @ D @ np.linalg.inv(eigVecs)

print(A_reconstructed)

[[ 6.  8.]
 [ 2. 12.]]

Eigendecomposição em R

A eigendecomposição no R pode ser realizada usando a função integrada eigen() e, portanto, não há necessidade de instalar e importar um pacote para a eigendecomposição de matrizes pequenas. O código a seguir no R executa a eigendecomposição na matriz A (o R classifica os valores próprios em ordem decrescente, de modo que a ordem dos vetores próprios é diferente da saída do Python NumPy):

A <- matrix(c(6,8,2,12), 2,2, byrow = TRUE)

print(A)

eDecomp <- eigen(A)
eigValues <- eDecomp$values
eigVectors <- eDecomp$vectors

print(eigValues)
print(eigVectors)

[1] 14  4
           [,1]       [,2]
[1,] -0.7071068 -0.9701425
[2,] -0.7071068  0.2425356

A_Reconstructed <- eigVectors %*% diag(eigValues) %*% (solve(eigVectors))

print(A_Reconstructed)

Show in New Window
     [,1] [,2]
[1,]    6    8
[2,]    2   12

Eigendecomposition vs. Decomposição de valor singular (SVD)

A eigendecomposição e as decomposições de valor singular (SVD) são dois métodos de fatoração de matriz notáveis usados em aprendizado de máquina e computação científica. Embora esses dois métodos fatorem uma matriz em três matrizes, eles têm algumas diferenças:

• A eigendecomposição só se aplica a matrizes quadradas, enquanto a SVD pode ser aplicada a matrizes quadradas e retangulares.
• Na SVD, as matrizes resultantes incluem pontuações singulares, enquanto as da eigendecomposição incluem valores próprios.
• Como a SVD pode acomodar matrizes não quadradas, ela tem aplicações mais amplas do que a eigendecomposição.

Conclusão

Neste breve artigo sobre álgebra linear, aprendemos sobre a eigendecomposição, como realizá-la com caneta e papel e como calculá-la usando Python e R. Aprendemos como a eigendecomposição é usada em algoritmos de aprendizado de máquina, como PCA. 

Se você estiver muito interessado em se tornar um analista ou cientista de dados, recomendo que faça o curso Álgebra linear para ciência de dados em R para ter uma base sólida em matemática aplicada e programação. Além disso, inscreva-se em nossa carreira completa de Cientista de Aprendizado de Máquina em Python para explorar o aprendizado supervisionado, não supervisionado e profundo.