Excel RSQ(): Den Bestimmtheitsmaß in Excel finden

Wenn du mit Trendlinien arbeitest oder messen musst, wie eng zwei Wertesätze zusammenhängen, ist die Funktion „ RSQ() “ in Excel ein praktisches Tool für diese Aufgabe. Der „ RSQ() “ sagt dir, wie viel der Abweichung in einem Bereich durch einen anderen erklärt werden kann. Im Grunde genommen bekommst du den R-Quadrat-Wert für zwei Reihen. Das ist super nützlich, von der Verkaufsanalyse bis hin zu wissenschaftlichen Experimenten.

Was macht RSQ()?

RSQ(), kurz für „R-Quadrat“, gibt das Quadrat des Pearson-Produkt-Moment-Korrelationskoeffizienten zwischen zwei Arrays zurück, der in diesem Fall auch der Bestimmtheitsmaß ist. Einfach gesagt, zeigt es, wie gut die Werte in einem Bereich die Werte in einem anderen Bereich vorhersagen. Wenn das Ergebnis von „ RSQ() “ 1 ist, hast du eine perfekte lineare Beziehung. Wenn der Wert 0 ist, gibt's überhaupt keinen linearen Zusammenhang.

Leute benutzen oft die „ RSQ() ”, wenn sie checken wollen, wie gut eine Linie zu ihren Daten passt, wie bei der Regressionsanalyse oder beim Zeichnen von Trendlinien.

RSQ() Syntax und Argumente

Hier ist die Struktur für „ RSQ() “:

=RSQ(known_y’s, known_x’s)

• known_y’s: Das sind deine abhängigen Werte (die, die du vorhersagen oder erklären willst).

• known_x’s: Das sind deine unabhängigen Werte (die, von denen du denkst, dass sie die Erklärung liefern könnten).

Beide Bereiche sollten die gleiche Anzahl an Datenpunkten haben. Wenn nicht, bekommst du die Fehlermeldung „ RSQ() “.

Wichtiger Hinweis: Wenn du dich mit den Ideen der einfachen linearen Regression und der gewöhnlichen linearen Regression der kleinsten Quadrate im Allgemeinen auskennst, wirst du vielleicht bemerken, dass die Funktion „ RSQ() “ nur einen Satz von x-Werten akzeptiert. Das liegt daran, dass „ RSQ() “ keine multiple lineare Regression unterstützt.

RSQ() Beispiel

Angenommen, du willst wissen, wie gut Werbeausgaben den Umsatz vorhersagen können.

• Spalte A: Werbeausgaben
• Spalte B: Verkäufe

Angenommen,deine Daten sehen so aus:

Wenn deine Datenfür Werbung in A2:A5 und für den Verkauf in B2:B5 stehen, gibst du Folgendes ein:

=RSQ(A2:A5, B2:B5)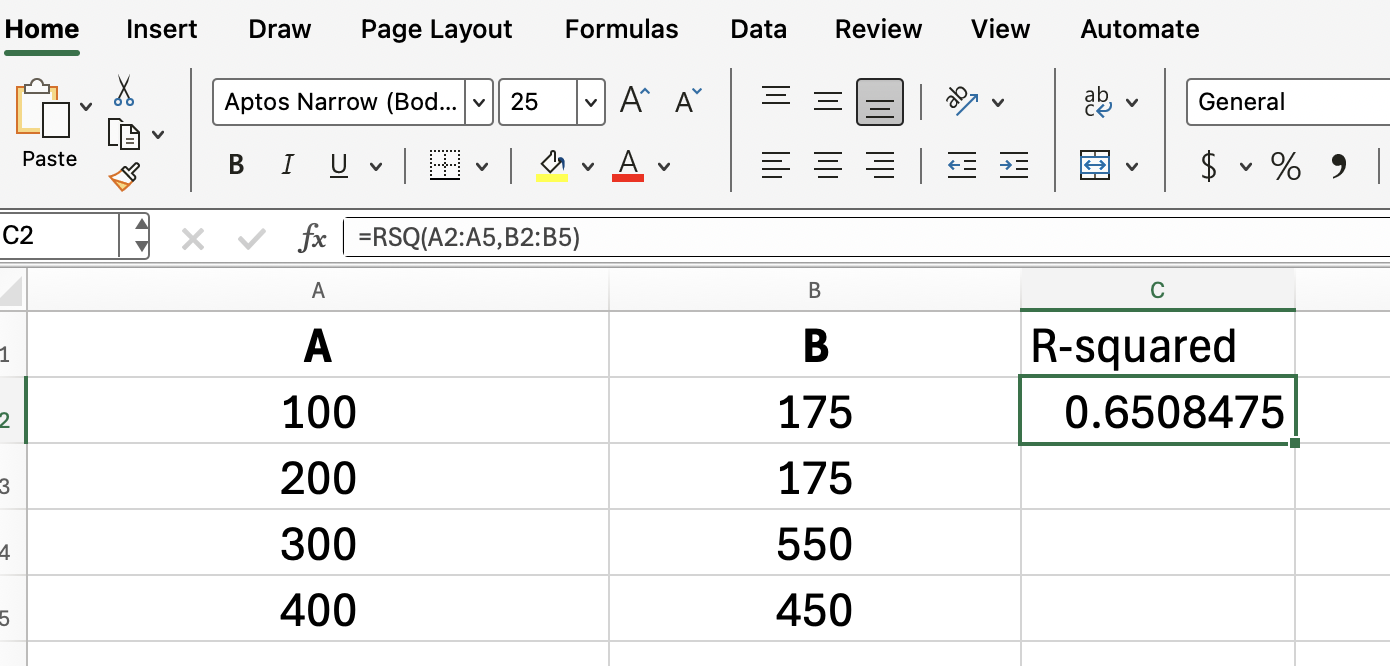

Diese Formel gibt den R-Quadrat-Wert zurück, der zeigt, wie viel der Veränderung im Umsatz durch die Veränderung der Werbeausgaben erklärt werden kann.

Ergebnisse von RSQ() interpretieren

• RSQ() = 1: Es gibt eine perfekte lineare Beziehung. Eine Variable sagt die andere ohne Fehler voraus.
• RSQ() = 0: Zwischen deinen beiden Datensätzen gibt's keinen linearen Zusammenhang.
• Werte zwischen 0 und 1: Je näher der Wert an 1 ist, desto stärker ist die lineare Beziehung.

Wenn wir uns im obigen Beispiel vorstellen würden, dass jede Zahl in Spalte B doppelt so hoch ist wie die entsprechende Zahl in Spalte A, dann würde die Regression auf einer geraden Linie liegen und eine Verdopplung der Werbung würde immer zu einer Verdopplung des Umsatzes führen. (Wie cool wäre das denn!)

Häufige Fehler, die Leute machen

Hier sind ein paar Probleme, die bei „ RSQ() “ auftreten können:

• Unterschiedliche Reichweiten: Wenn deine beiden Bereiche nicht die gleiche Anzahl an Zeilen haben, gibt „ RSQ() “ einen Fehler „ #N/A “ zurück.

• Leere oder nicht numerische Zellen: Leere Zellen oder Text innerhalb der Bereiche werden einfach ignoriert, aber wenn zu viele fehlen, kann das zu falschen Ergebnissen oder Fehlern führen. Das kann ein subtiler Fehler sein, also pass gut auf!

• Einzelner Datenpunkt: „ RSQ() “ braucht mindestens zwei Zahlenpaare. Wenn nicht, bekommst du die Fehlermeldung „ #DIV/0! “. Das liegt daran, dass Varianz/Kovarianz mit nur einem Wert nicht definiert wäre.

Wenn dir was komisch vorkommt, check nochmal, ob du dich vertippt hast oder was fehlt.

RSQ() vs. CORREL()

Du fragst dich vielleicht, warum du RSQ() statt CORREL() verwenden solltest. Hier ist der Unterschied:

• CORREL() gibt den Pearson-Korrelationskoeffizienten (r) zurück, der die Stärke und Richtung einer linearen Beziehung misst.

• RSQ() gibt den R-Quadrat-Wert (R²) zurück.²) zurück, sodass du immer einen Wert zwischen 0 und 1 bekommst, der sich nur auf den Anteil der erklärten Varianz konzentriert.

Wenn du nur sehen willst, ob deine Variablen sich zusammen bewegen (positiv oder negativ), findest du unter CORREL() mehr Details. Wenn du messen willst, wie viel der Veränderung einer Variablen durch eine andere erklärt wird, ist der Korrelationskoeffizient ( RSQ() ) genau das Richtige für dich.

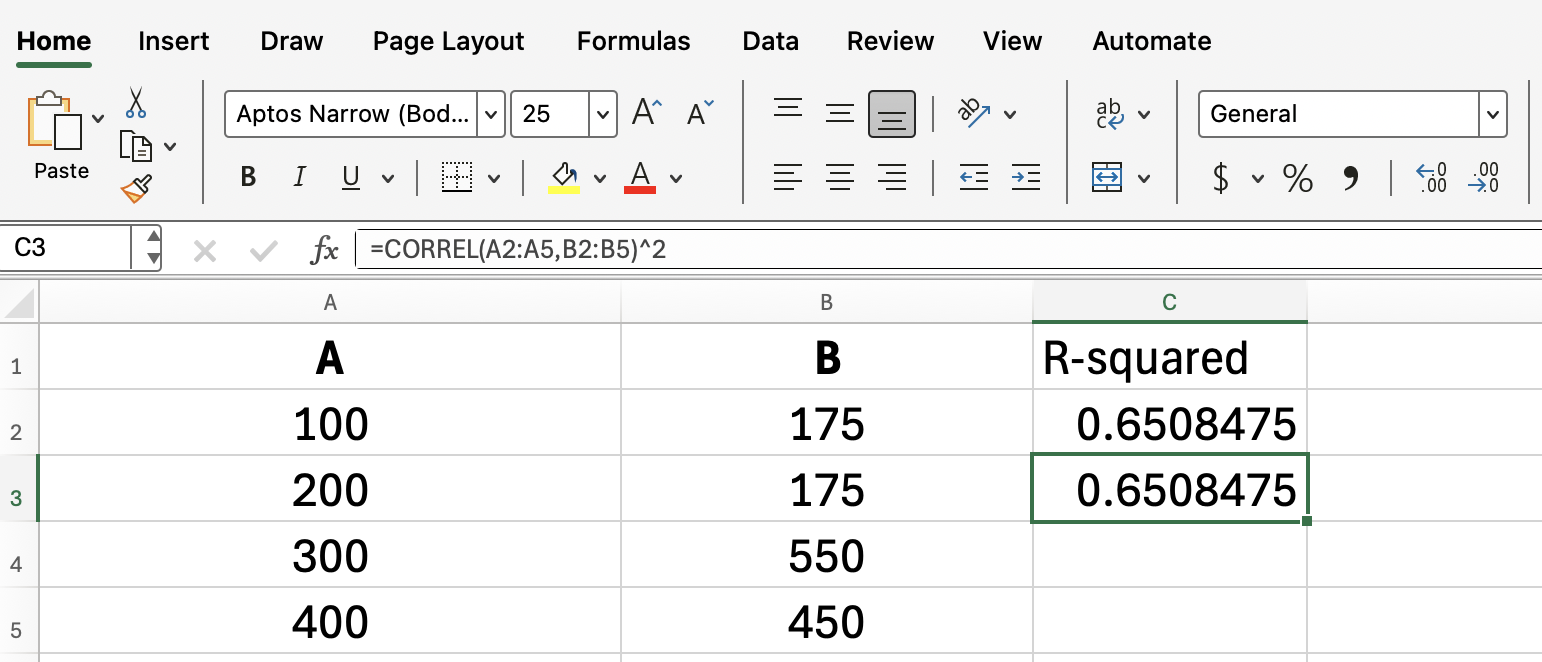
Da wir es hier mit einer einfachen linearen Regression zu tun haben, können wir den R-Quadrat-Wert immer einfach durch Quadrieren des Ergebnisses von „ CORREL() “ ermitteln:

=CORREL(A2:A5, B2:B5)^2

RSQ() und Streudiagramme

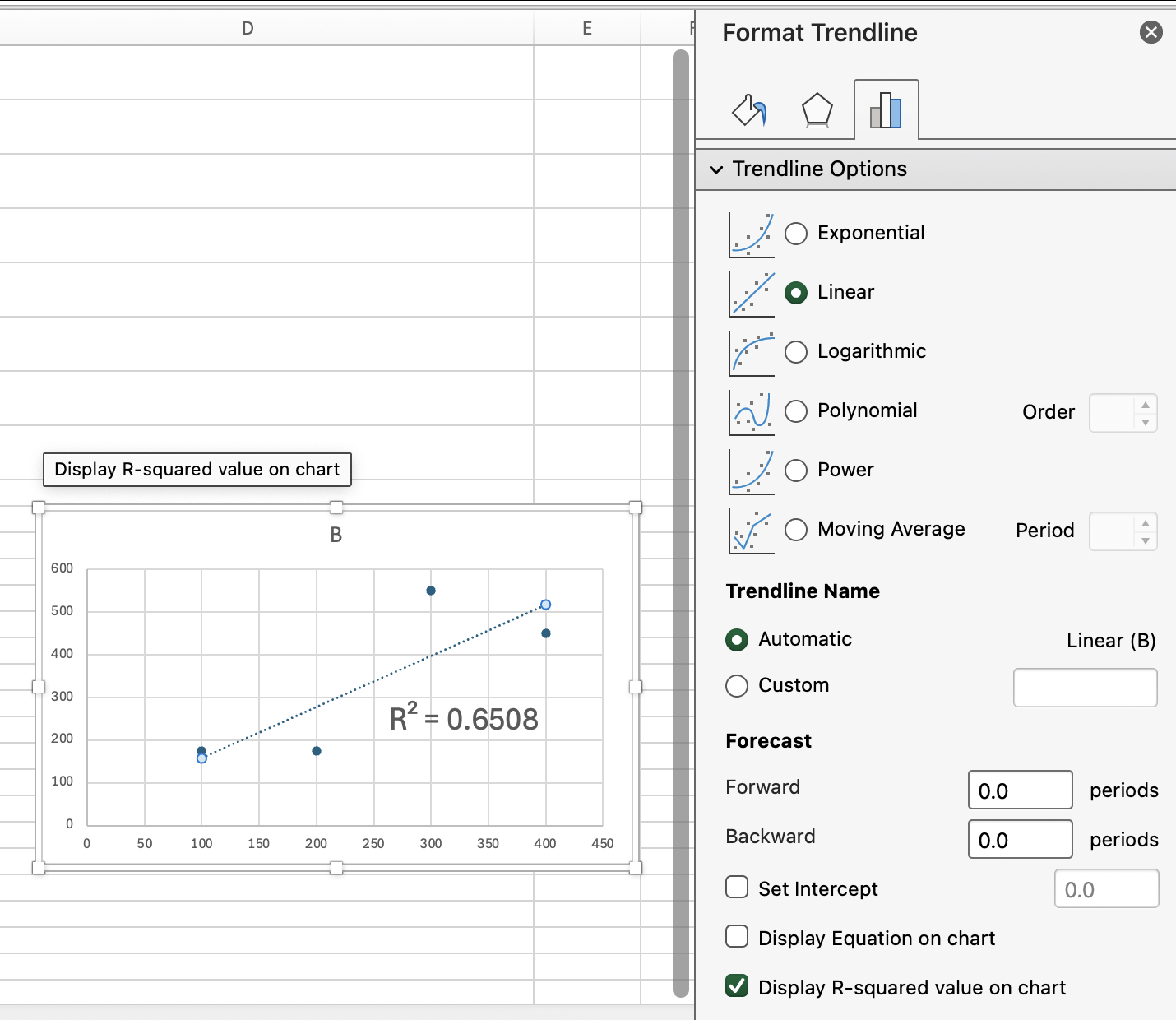
Wenn du schon mal eine Trendlinie zu einem Streudiagramm in Excel hinzugefügt hast, hast du vielleicht den R-Quadrat-Wert direkt im Diagramm gesehen. Das ist derselbe Wert, den „ RSQ() “ mit deinen Datenbereichen zurückgibt.

Wenn du den R-Quadrat-Wert in deinem Arbeitsblatt anzeigen willst, ohne ein Diagramm hinzuzufügen, gib einfach „ RSQ() “ direkt in eine Zelle ein. So kannst du besser mit der Zahl arbeiten.

Wenn du nicht ganz sicher bist, wie du mit coolen Visualisierungen in Excel umgehen sollst, schreib dich in unseren Kurs „Datenvisualisierung in Excel” ein, der alles Wichtige im Detail erklärt.

Praktische Tipps

Zum Abschluss der technischen Anleitung hier noch ein paar praktische Tipps:

• Beschrifte deine Daten klar, damit du die X- und Y-Werte nicht verwechselst.
• Überprüfe immer, ob deine Bereiche gleich groß sind, bevor du die Formel eingibst.
• Wenn du mehr als zwei Variablen vergleichen willst, solltest du Regressionsanalyse-Tools wie das Datenanalyse-Toolpaket oder die Funktion „ LINEST() “ ausprobieren. LINEST() gibt auch andere Modellkennzahlen wie die F-Statistik und Standardfehler an.

Fazit

Wie du gesehen hast, ist „ RSQ() “ eine einfache, aber effektive Methode, um in Excel zu messen, wie gut eine Reihe von Werten eine andere vorhersagt. Damit kannst du echt viel machen, zum Beispiel Trends analysieren oder Ergebnisse vorhersagen. Überlass das nicht dem Zufall.

Als nächsten Schritt solltest du unsere Kurse „Datenanalyse in Excel“ und „Erweiterte Excel-Funktionen“ machen, um deine Excel-Kenntnisse (und deine Statistikkenntnisse) weiter zu verbessern!