Excel RSQ(): Encuentra el coeficiente de determinación en Excel

Si trabajas con líneas de tendencia o necesitas medir la relación entre dos conjuntos de valores, la función « RSQ() » (Correlación) de Excel es una herramienta sencilla para realizar esta tarea. La correlación ( RSQ() ) indica en qué medida la variación de un rango puede explicarse por otro. Básicamente, te da el valor R cuadrado para dos series. Esto resulta útil en todo, desde análisis de ventas hasta experimentos científicos.

¿Qué hace RSQ()?

RSQ(), abreviatura de «R al cuadrado», devuelve el cuadrado del coeficiente de correlación producto-momento de Pearson entre dos arreglos, que en este caso es también el coeficiente de determinación. En términos sencillos, muestra qué tan bien los valores en un rango predicen los valores en otro. Si el resultado de la prueba de correlación de RSQ() es 1, tienes una relación lineal perfecta. Si es 0, no existe ninguna relación lineal.

La gente suele utilizar la « RSQ() » cuando quiere comprobar si una línea se ajusta bien a los datos, como en el análisis de regresión o al gráficar líneas de tendencia.

Sintaxis y argumentos de RSQ()

Esta es la estructura de RSQ():

=RSQ(known_y’s, known_x’s)

• known_y’s: Estos son tus valores dependientes (los que intentas predecir o explicar).

• known_x’s: Estos son tus valores independientes (los que crees que podrían estar dando la explicación).

Ambos rangos deben tener el mismo número de puntos de datos. Si no es así, RSQ() te dará un error.

Nota importante que debo hacer: Si estás familiarizado con los conceptos de regresión lineal simple y, en general, con la regresión lineal por mínimos cuadrados ordinarios, habrás observado que la función RSQ() solo admite un conjunto de valores x. Esto se debe a que RSQ() no admite la regresión lineal múltiple.

Ejemplo de RSQ()

Supongamos que quieres saber en qué medida el gasto en publicidad predice las ventas.

• Columna A: Gasto publicitario
• Columna B: Ventas

Supongamos quetus datos tienen este aspecto:

Si tus datosestán en A2:A5 para publicidad y en B2:B5 para ventas, introducirías:

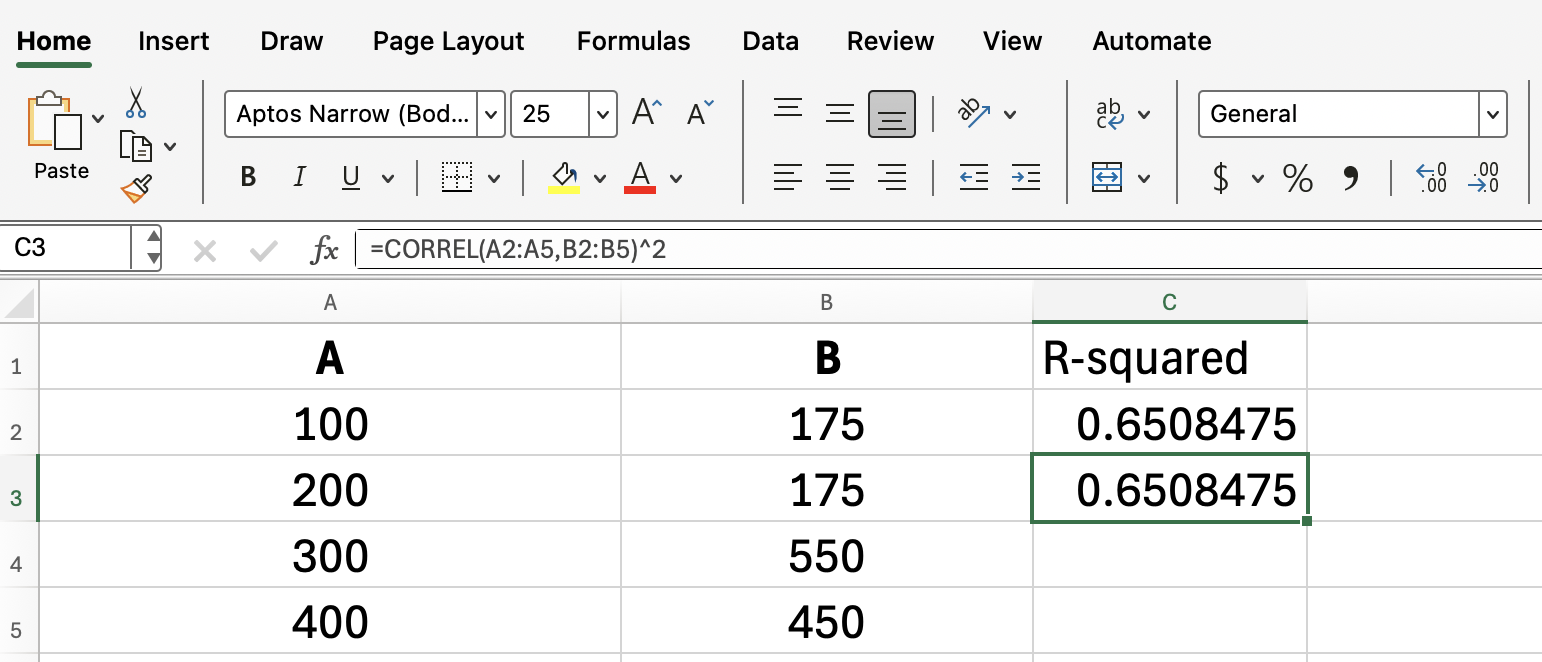
=RSQ(A2:A5, B2:B5)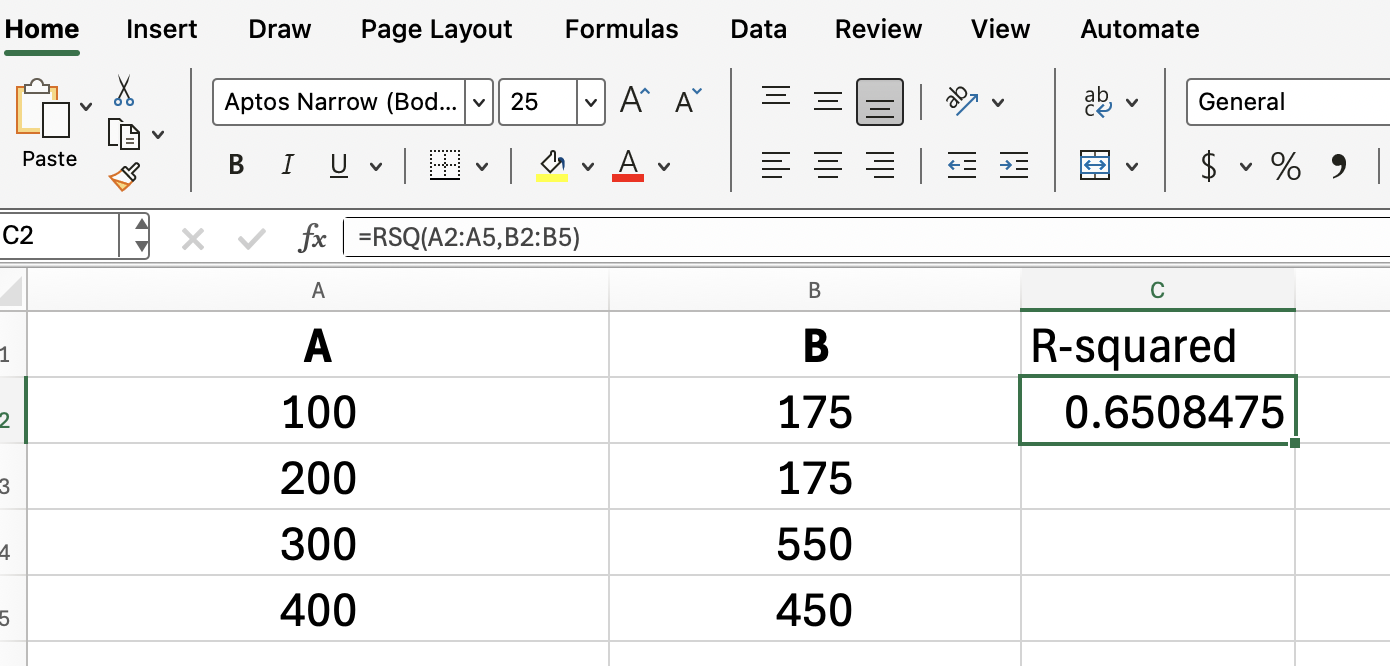

Esta fórmula devuelve el valor R cuadrado, que muestra qué parte del cambio en las ventas puede explicarse por el cambio en el gasto publicitario.

Interpretación de los resultados de RSQ()

• RSQ() = 1: Existe una relación lineal perfecta. Una variable predice la otra sin error.
• RSQ() = 0: No existe una relación lineal entre tus dos conjuntos de datos.
• Valores entre 0 y 1: Cuanto más se acerque a 1, más fuerte será la relación lineal.

Si imagináramos en el ejemplo anterior que cada número de la columna B fuera el doble del número correspondiente de la columna A, la regresión se situaría en una línea recta y duplicar la publicidad siempre duplicaría las ventas. (¡Qué genial sería!)

Errores comunes que comete la gente

A continuación, se indican algunos problemas que pueden surgir con RSQ():

• Tamaños de rango desiguales: Si los dos rangos no tienen el mismo número de filas, RSQ() devolverá un error « #N/A » (No se han encontrado filas en el rango).

• Celdas vacías o sin números: Las celdas en blanco o el texto dentro de los rangos se ignoran, pero si faltan demasiados, los resultados pueden ser engañosos o pueden aparecer errores. Este puede ser un error más sutil, ¡así que ten cuidado!

• Punto de datos único: « RSQ() » necesita al menos dos pares de números. Si no es así, aparecerá el error « #DIV/0! » (No se ha encontrado el archivo o la carpeta). Esto se debe a que la varianza/covarianza no estaría definida con un solo valor.

Si algo parece incorrecto, comprueba dos veces los rangos para ver si hay errores tipográficos o entradas que falten.

RSQ() vs. CORREL()

Quizás te preguntes por qué utilizar RSQ() en lugar de CORREL(). Esta es la diferencia:

• CORREL() devuelve el coeficiente de correlación de Pearson (r), que mide la fuerza y la dirección de una relación lineal.

• RSQ() devuelve el R cuadrado (R²), por lo que siempre te da un valor entre 0 y 1, centrándose únicamente en la proporción de varianza explicada.

Si solo quieres ver si tus variables se mueven juntas (positiva o negativamente), CORREL() te ofrece más detalles. Si estás midiendo cuánto del cambio en una variable se explica por otra, lo que necesitas es el coeficiente de correlación ( RSQ() ).

Dicho esto, dado que estamos trabajando con una regresión lineal simple, siempre podemos hallar el R cuadrado simplemente elevando al cuadrado el resultado de CORREL():

=CORREL(A2:A5, B2:B5)^2

RSQ() y diagramas de dispersión

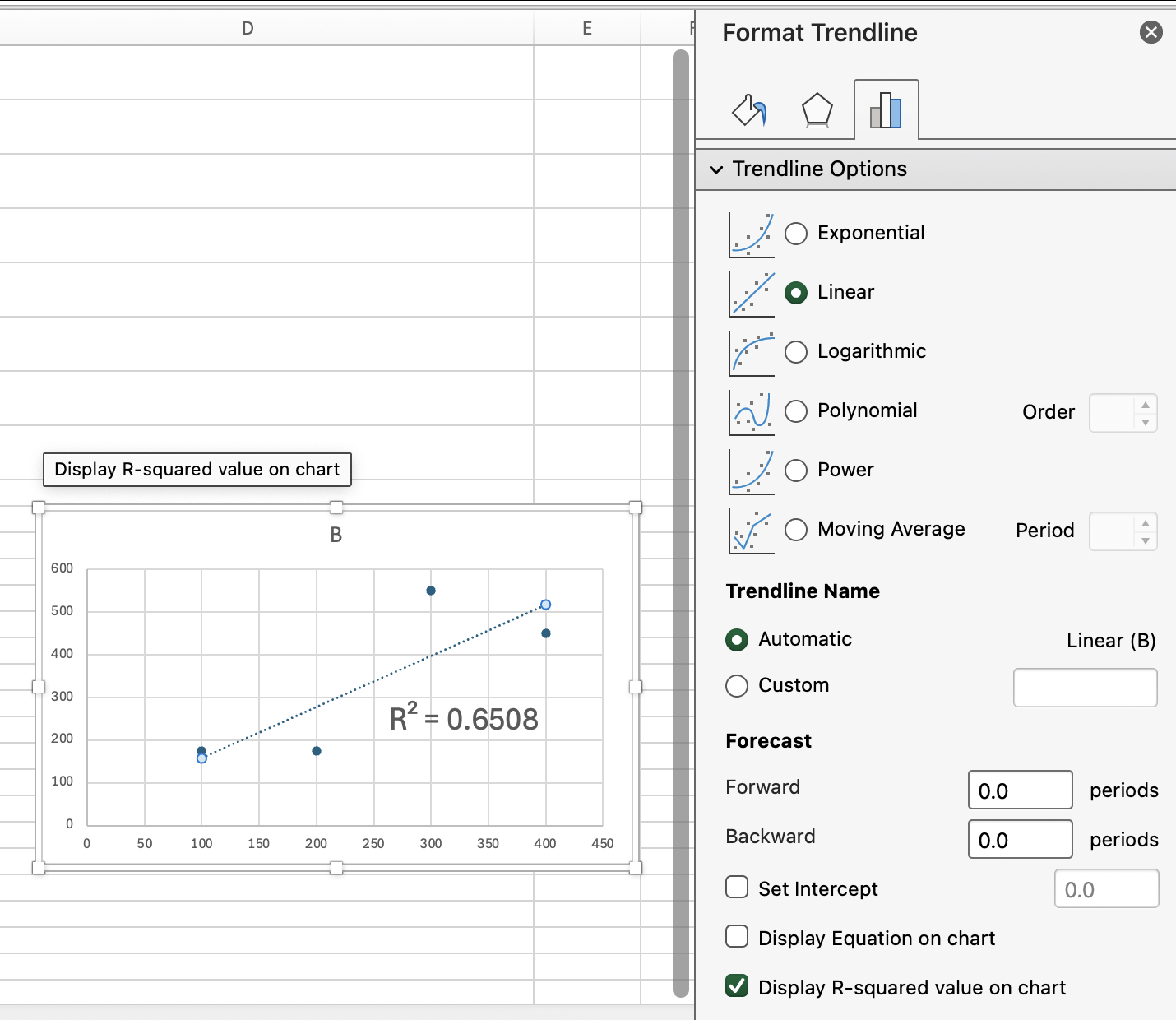
Si alguna vez has añadido una línea de tendencia a un gráfico de dispersión en Excel, es posible que hayas visto el valor R cuadrado que aparece en el gráfico. Es el mismo valor que devuelve RSQ() con tus rangos de datos.

Si deseas mostrar el R cuadrado en tu hoja de cálculo sin añadir un gráfico, solo tienes que utilizar RSQ() directamente en una celda. De esta manera, es un número con el que puedes trabajar más fácilmente.

Si no tienes del todo claro cómo trabajar con elementos visuales atractivos en Excel, inscríbete en nuestro curso Visualización de datos en Excel, que cubre todos los aspectos importantes en detalle.

Consejos prácticos

Para concluir con la orientación técnica, aquí tienes algunos consejos prácticos:

• Etiqueta claramente tus datos para mantener las X y las Y en su sitio.
• Comprueba siempre que los rangos sean del mismo tamaño antes de introducir la fórmula.
• Si deseas comparar más de dos variables, considera utilizar herramientas de análisis de regresión como el paquete de herramientas de análisis de datos o la función « LINEST() » (Regresión por pasos). LINEST() también informa sobre otras métricas del modelo, como la estadística F y los errores estándar.

Conclusión

Como has descubierto, « RSQ() » es una forma sencilla pero eficaz de medir en Excel la capacidad de un conjunto de valores para predecir otro. Se pueden hacer muchas cosas con él, como analizar tendencias o pronosticar resultados. No te lo dejes a la suerte.

Como siguiente paso, ¡realiza nuestros cursos Análisis de datos en Excel y Funciones avanzadas de Excel para seguir mejorando tus habilidades con Excel (y las estadísticas)!