Excel RSQ(): Descubra o Coeficiente de Determinação no Excel

RSQ() Se você trabalha com linhas de tendência ou precisa medir a proximidade entre dois conjuntos de valores, a função “ RSQ() ” (Correlação) do Excel é uma ferramenta simples para o trabalho. A correlação indica a proporção da variação em um intervalo que pode ser explicada por outro. Basicamente, dá o valor R-quadrado para duas séries. Isso é útil em tudo, desde análises de vendas até experimentos científicos.

O que faz o RSQ()?

RSQ(), abreviação de “R-quadrado”, retorna o quadrado do coeficiente de correlação produto-momento de Pearson entre duas matrizes, que neste caso também é o coeficiente de determinação. Em termos simples, mostra como os valores de um intervalo podem prever os de outro. Se o resultado do teste de linearidade ( RSQ() ) for 1, você tem uma relação linear perfeita. Se for 0, não tem nenhuma relação linear.

As pessoas costumam usar a RSQ() quando querem ver se uma linha se encaixa bem nos dados, tipo em análises de regressão ou quando estão fazendo gráficos de tendências.

Sintaxe e argumentos de RSQ()

Aqui tá a estrutura do RSQ():

=RSQ(known_y’s, known_x’s)

• known_y’s: Esses são os teus valores dependentes (aqueles que você está tentando prever ou explicar).

• known_x’s: Esses são os teus valores independentes (aqueles que achas que podem estar explicando).

Ambas as gamas devem ter o mesmo número de pontos de dados. Se não estiverem, você vai ver um erro em RSQ().

Observação importante que eu preciso fazer: Se você já conhece as ideias de regressão linear simples e, de forma mais geral, de regressão linear por mínimos quadrados ordinários, pode notar que a função RSQ() só aceita um conjunto de valores x. Isso é porque o RSQ() não dá conta de regressão linear múltipla.

Exemplo de RSQ()

Digamos que você queira saber se os gastos com publicidade ajudam a prever as vendas.

• Coluna A: Gastos com publicidade
• Coluna B: Vendas

Digamos queseus dados sejam assim:

Se seus dadosestiverem em A2:A5 para publicidade e B2:B5 para vendas, você deve digitar:

=RSQ(A2:A5, B2:B5)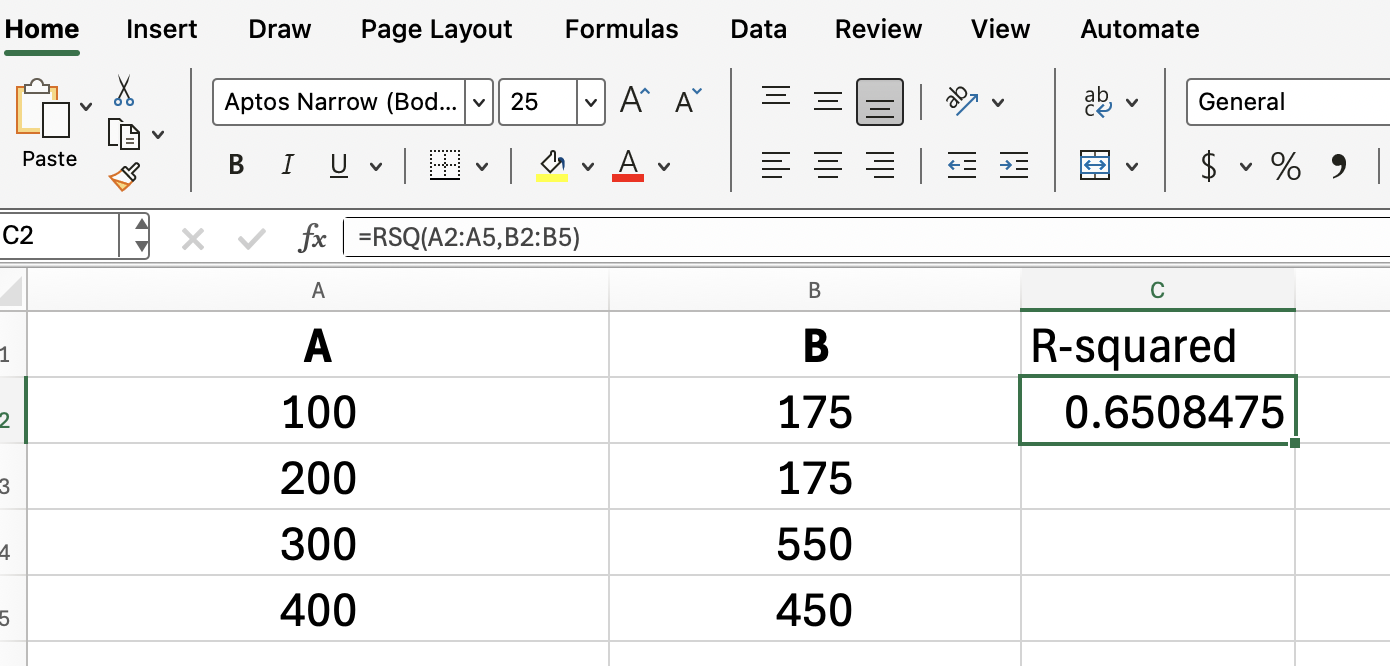

Essa fórmula mostra o valor R-quadrado, que é a proporção da variação nas vendas que pode ser explicada pela variação nos gastos com publicidade.

Interpretando os resultados do RSQ()

• RSQ() = 1: Tem uma relação linear perfeita. Uma variável prevê a outra sem erro.
• RSQ() = 0: Não tem relação direta entre os dois conjuntos de dados.
• Valores entre 0 e 1: Quanto mais perto de 1, mais forte é a relação linear.

Se imaginássemos no exemplo acima que todos os números da coluna B fossem o dobro dos números correspondentes na coluna A, a regressão ficaria numa linha reta e dobrar a publicidade sempre dobraria as vendas. (Que legal que seria!)

Erros comuns que as pessoas cometem

Aqui estão alguns problemas que você pode encontrar com RSQ():

• Tamanhos de intervalos diferentes: Se os dois intervalos não tiverem o mesmo número de linhas, a função “ RSQ() ” vai mostrar um erro “ #N/A ”.

• Células vazias ou sem números: Células em branco ou texto dentro dos intervalos são ignorados, mas se faltar muitos, os resultados podem ser confusos ou podem aparecer erros. Esse pode ser um erro mais sutil, então toma cuidado!

• Um único dado: “ RSQ() ” precisa de pelo menos dois pares de números. Se não, você vai ver um erro “ #DIV/0! ”. Isso é porque a variância/covariância não teria sentido com só um valor.

Se algo parecer errado, dá uma olhada nas faixas pra ver se tem erros de digitação ou entradas faltando.

RSQ() vs. CORREL()

Você pode estar se perguntando por que usar RSQ() em vez de CORREL(). A diferença é essa:

• CORREL() retorna o coeficiente de correlação de Pearson (r), que mede a força e a direção de uma relação linear.

• RSQ() retorna o R-quadrado (R²), então sempre dá um valor entre 0 e 1, focando só na proporção da variância explicada.

Se você só quer ver se suas variáveis se movem juntas (positivo ou negativo), o site CORREL() dá mais detalhes. Se você está medindo quanto da mudança em uma variável é explicada por outra, o que você precisa é de um coeficiente de correlação ( RSQ() ).

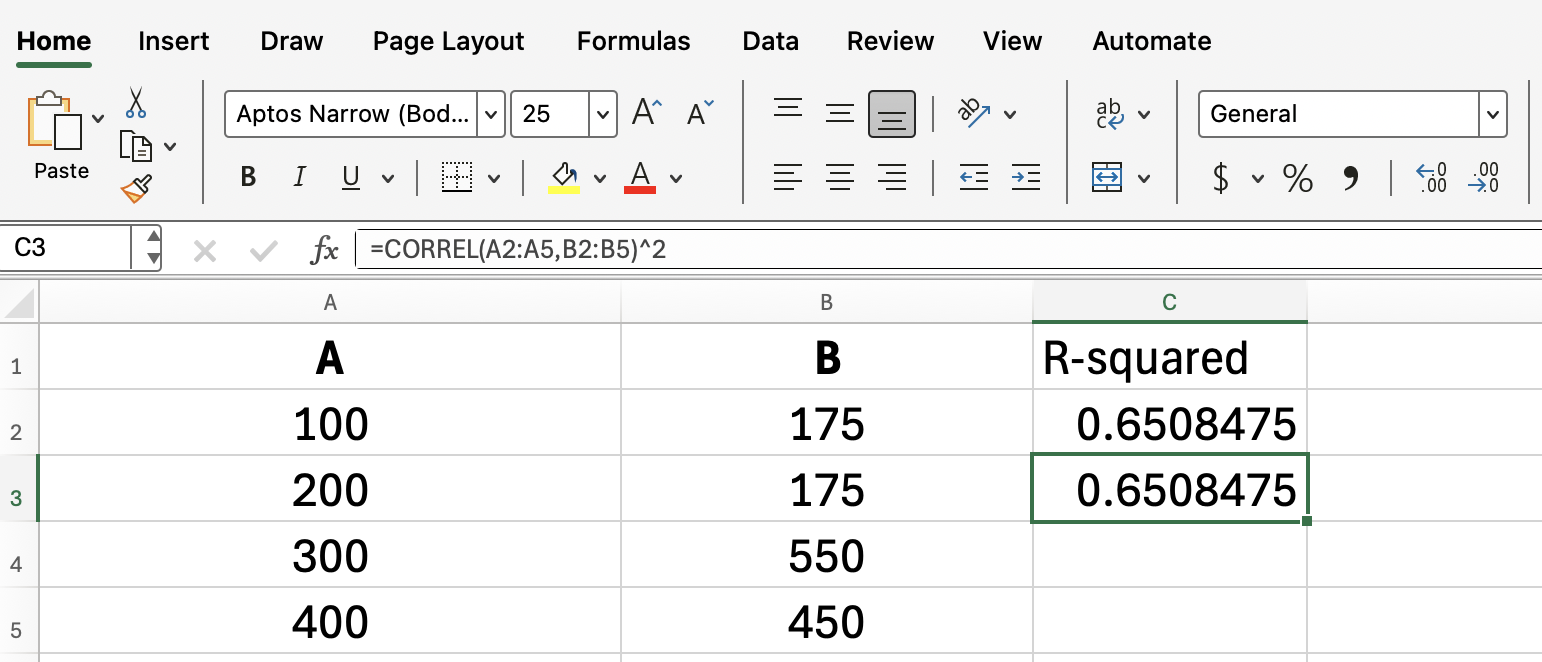
Dito isso, como estamos lidando com uma regressão linear simples, sempre podemos encontrar o R-quadrado só de elevar ao quadrado o resultado de CORREL():

=CORREL(A2:A5, B2:B5)^2

RSQ() e gráficos de dispersão

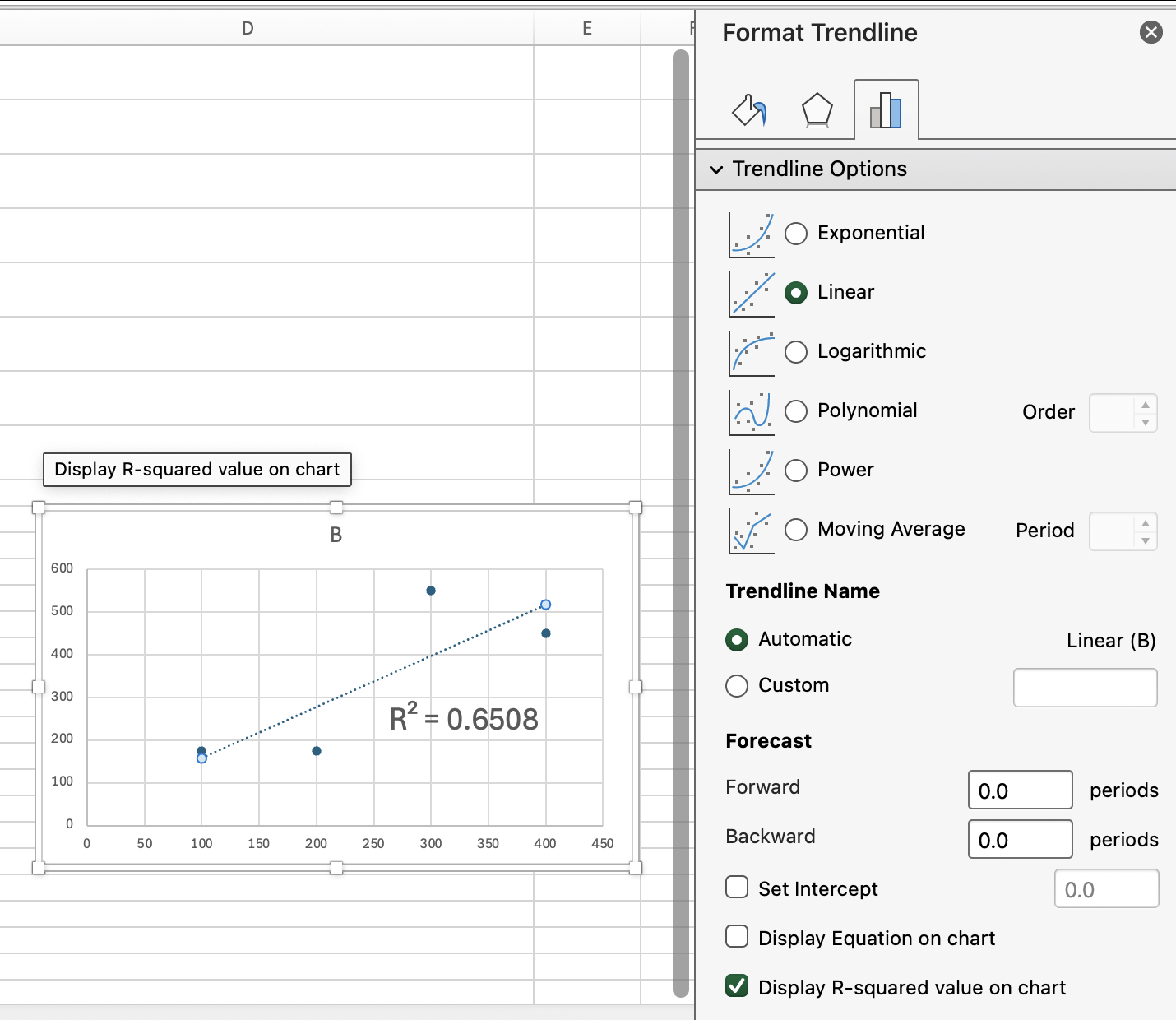
Se você já adicionou uma linha de tendência a um gráfico de dispersão no Excel, deve ter visto o valor R-quadrado aparecendo bem no gráfico. É o mesmo valor que o comando “ RSQ() ” mostra com os teus intervalos de dados.

Se você quiser mostrar o R-quadrado na sua planilha sem adicionar um gráfico, é só usar RSQ() direto numa célula. Assim, é um número com o qual você pode trabalhar mais facilmente.

Se você não está 100% certo sobre como realmente trabalhar com visuais legais no Excel, inscreva-se no nosso curso Visualização de dados no Excel, que cobre tudo o que é importante em detalhes.

Dicas práticas

Pra fechar a orientação técnica, aqui vão algumas dicas práticas:

• Identifique claramente seus dados para manter os X e os Y organizados.
• Sempre dá uma conferida se os intervalos têm o mesmo tamanho antes de colocar a fórmula.
• Se você quer comparar mais de duas variáveis, pense em usar ferramentas de análise de regressão, como o Data Analysis Toolpak ou a função “ LINEST() ”. LINEST() também mostra outras métricas do modelo, como a estatística F e os erros padrão.

Conclusão

Como você já viu, a regressão linear simples ( RSQ() ) é uma maneira direta e eficaz de medir como um conjunto de valores prevê outro no Excel. Dá pra fazer um monte de coisas com isso, tipo analisar tendências ou prever resultados. Não deixe isso pra adivinhação.

Depois, dá uma olhada nos nossos cursos Análise de Dados no Excel e Funções Avançadas do Excel pra continuar melhorando suas habilidades no Excel (e em estatística)!