Excel RSQ() : Déterminer le coefficient de détermination dans Excel

RSQ() Si vous travaillez avec des courbes de tendance ou si vous devez mesurer le degré de corrélation entre deux ensembles de valeurs, la fonction « Corrélation » d'Excel est un outil simple qui vous sera très utile. RSQ() vous indique dans quelle mesure la variation d'une plage peut s'expliquer par une autre. En substance, cela vous donne la valeur R au carré pour deux séries. Cela est utile dans tous les domaines, de l'analyse des ventes aux expériences scientifiques.

Que fait la fonction RSQ() ?

RSQ(), abréviation de « R au carré », renvoie le carré du coefficient de corrélation produit-moment de Pearson entre deux tableaux, qui dans ce cas correspond également au coefficient de détermination. En termes simples, cela montre dans quelle mesure les valeurs d'une plage permettent de prédire celles d'une autre plage. Si le résultat de l'RSQ() e est 1, vous avez une relation linéaire parfaite. Si la valeur est 0, il n'y a aucune relation linéaire.

Les gens utilisent souvent l'RSQ() e lorsqu'ils souhaitent vérifier dans quelle mesure une ligne correspond à leurs données, comme dans l'analyse de régression ou lors de la représentation graphique de courbes de tendance.

Syntaxe et arguments de RSQ()

Voici la structure de l'RSQ():

=RSQ(known_y’s, known_x’s)

• known_y’s: Ce sont vos valeurs dépendantes (celles que vous essayez de prédire ou d'expliquer).

• known_x’s: Ce sont vos valeurs indépendantes (celles qui, selon vous, pourraient expliquer la situation).

Les deux plages doivent comporter le même nombre de points de données. Si ce n'est pas le cas, RSQ() affichera une erreur.

Remarque importante à noter: Si vous êtes familier avec les concepts de régression linéaire simple et, plus généralement, de régression linéaire par les moindres carrés ordinaires, vous remarquerez peut-être que la fonction RSQ() ne prend qu'un seul ensemble de valeurs x. En effet, RSQ() ne prend pas en charge la régression linéaire multiple.

Exemple RSQ()

Supposons que vous souhaitiez savoir dans quelle mesure les dépenses publicitaires permettent de prédire les ventes.

• Colonne A : Dépenses publicitaires
• Colonne B : Ventes

Supposons quevos données se présentent comme suit :

Si vos donnéesse trouvent dans A2:A5 pour la publicité et dans B2:B5 pour les ventes, vous devez saisir :

=RSQ(A2:A5, B2:B5)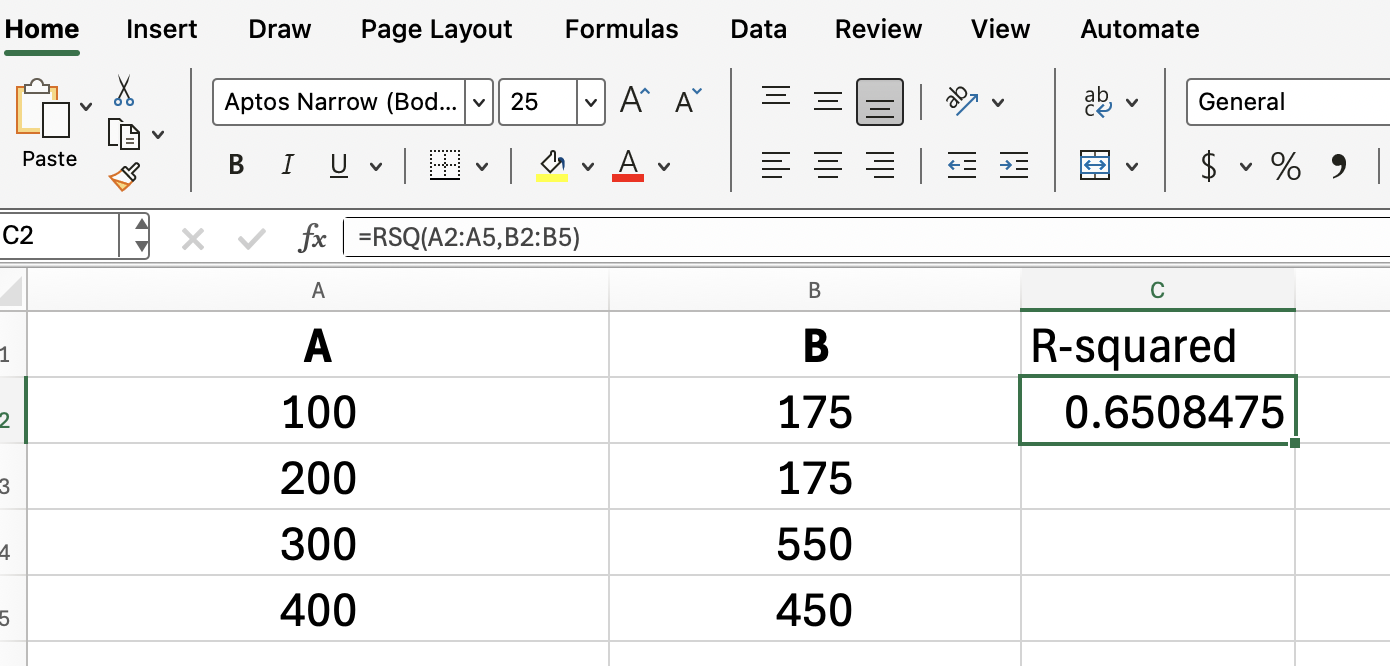

Cette formule renvoie la valeur R au carré, qui indique dans quelle mesure la variation des ventes peut s'expliquer par la variation des dépenses publicitaires.

Interprétation des résultats RSQ()

• RSQ() = 1: Il existe une relation linéaire parfaite. Une variable prédit l'autre sans erreur.
• RSQ() = 0 : Il n'existe aucune relation linéaire entre vos deux ensembles de données.
• Valeurs comprises entre 0 et 1 : Plus le chiffre est proche de 1, plus la relation linéaire est forte.

Si nous imaginions dans l'exemple ci-dessus que chaque nombre de la colonne B était le double du nombre correspondant dans la colonne A, alors la régression se situerait sur une ligne droite, et doubler la publicité doublerait toujours les ventes. (Ce serait formidable !)

Erreurs courantes commises par les personnes

Voici quelques problèmes que vous pourriez rencontrer avec l'RSQ():

• Tailles de gammes inégales : Si vos deux plages ne comportent pas le même nombre de lignes, RSQ() renvoie une erreur d'#N/A.

• Cellules vides ou non numériques : Les cellules vides ou le texte dans les plages sont ignorés, mais si trop d'éléments manquent, les résultats peuvent être trompeurs ou des erreurs peuvent apparaître. Il peut s'agir d'une erreur plus subtile, veuillez donc faire attention.

• Point de données unique : « RSQ() » nécessite au moins deux paires de chiffres. Dans le cas contraire, vous obtiendrez une erreur « #DIV/0! ». En effet, la variance/covariance serait indéfinie avec une seule valeur.

Si quelque chose semble incorrect, veuillez vérifier vos plages afin de vous assurer qu'il n'y a pas de fautes de frappe ou d'entrées manquantes.

RSQ() vs. CORREL()

Vous vous demandez peut-être pourquoi utiliser RSQ() plutôt que CORREL(). Voici la différence :

• CORREL() renvoie le coefficient de corrélation de Pearson (r), qui mesure la force et la direction d'une relation linéaire.

• RSQ() renvoie le R-carré (R²), ce qui vous donne toujours une valeur comprise entre 0 et 1, en se concentrant uniquement sur la proportion de variance expliquée.

Si vous souhaitez simplement vérifier si vos variables évoluent de manière parallèle (positive ou négative), veuillez consulter CORREL() pour obtenir plus de détails. Si vous souhaitez mesurer dans quelle mesure la variation d'une variable s'explique par une autre, l'RSQ() est ce qu'il vous faut.

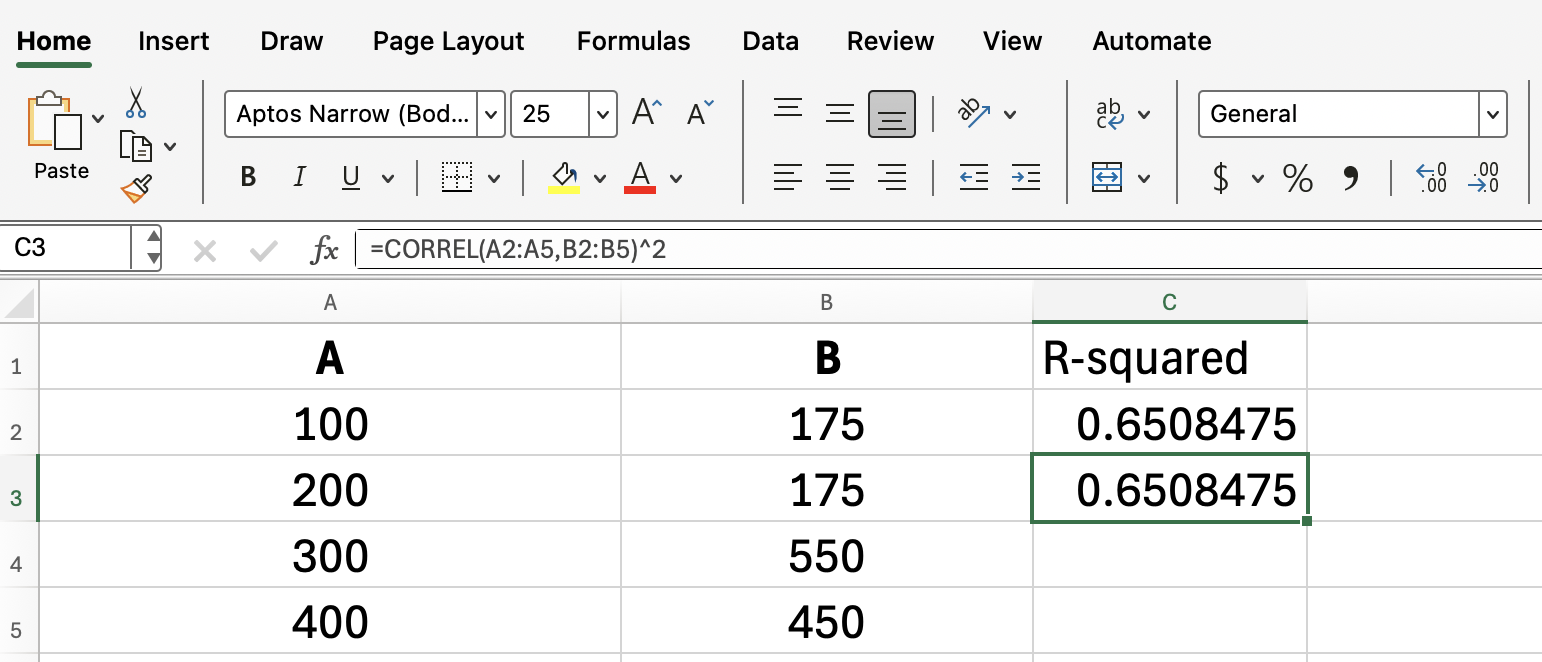
Cela étant dit, comme nous avons affaire à une régression linéaire simple, nous pouvons toujours trouver le R-carré en élevant au carré le résultat de l'CORREL():

=CORREL(A2:A5, B2:B5)^2

RSQ() et nuages de points

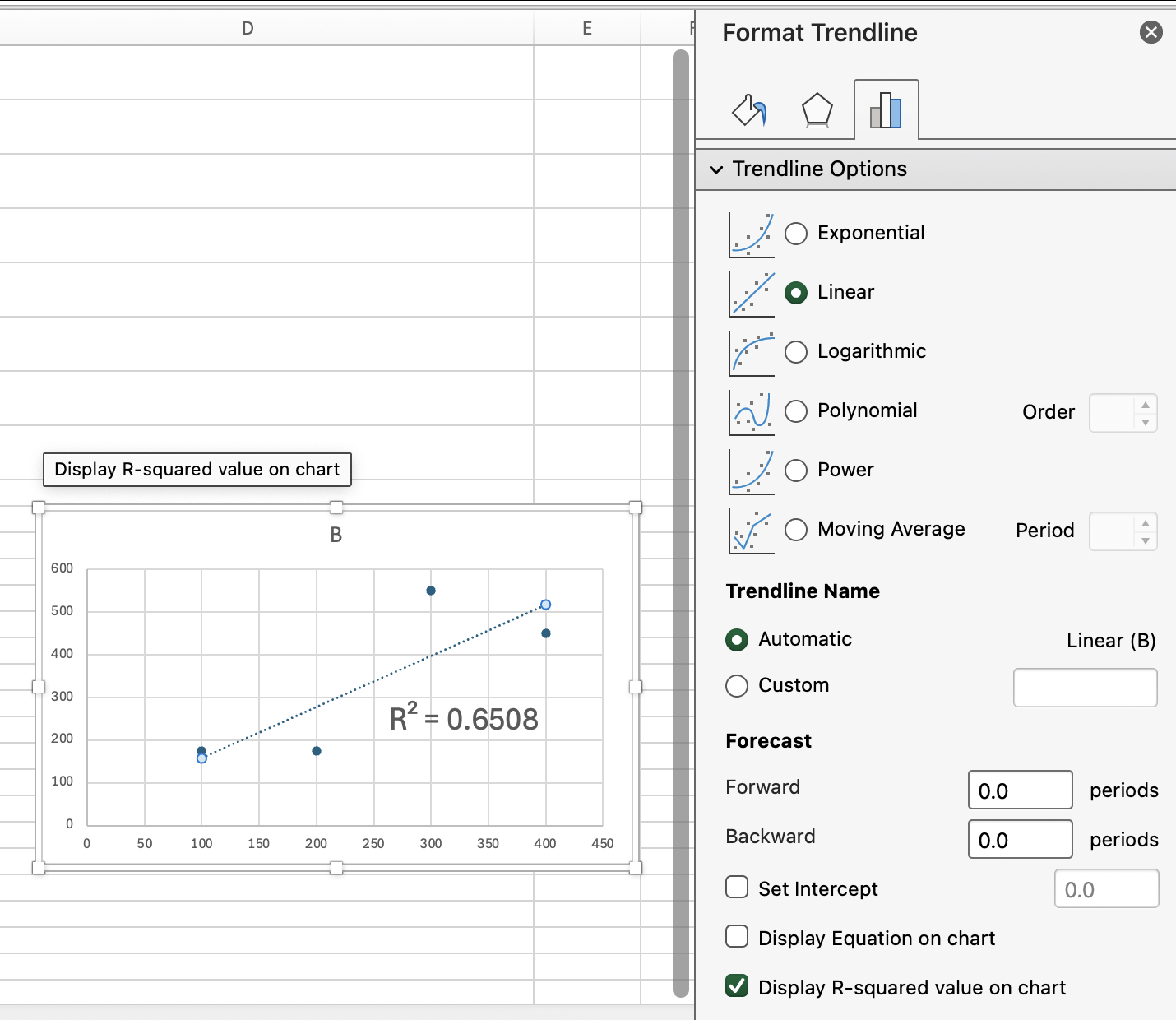
Si vous avez déjà ajouté une courbe de tendance à un graphique à nuages dispersés dans Excel, vous avez peut-être remarqué que la valeur R au carré s'affiche directement sur le graphique. C'est la même valeur que renvoie la fonction « RSQ() » avec vos plages de données.

Si vous souhaitez afficher le R-carré sur votre feuille de calcul sans ajouter de graphique, utilisez simplement RSQ() directement dans une cellule. De cette manière, il s'agit d'un nombre plus facile à manipuler.

Si vous n'êtes pas encore tout à fait sûr de savoir comment travailler efficacement avec des visuels attrayants dans Excel, inscrivez-vous à notre cours Visualisation des données dans Excel, qui couvre tous les aspects importants en détail.

Conseils pratiques

Pour conclure ces conseils techniques, voici quelques astuces pratiques :

• Étiquetez clairement vos données afin de ne pas confondre les X et les Y.
• Veuillez toujours vérifier que vos plages sont de la même taille avant de saisir la formule.
• Si vous souhaitez comparer plus de deux variables, envisagez d'utiliser des outils d'analyse de régression tels que le Data Analysis Toolpak ou la fonction « LINEST() ». LINEST() fournit également d'autres mesures du modèle, telles que la statistique F et les erreurs types.

Conclusion

Comme vous l'avez découvert, l'RSQ() est un moyen simple mais efficace de mesurer dans quelle mesure un ensemble de valeurs permet d'en prédire un autre dans Excel. Il existe de nombreuses possibilités, telles que l'analyse des tendances ou la prévision des résultats. Ne vous fiez pas aux suppositions.

Pour aller plus loin, nous vous recommandons de suivre nos cours Analyse de données dans Excel et Fonctions avancées d'Excel afin de continuer à améliorer vos compétences en Excel (et en statistiques) !