Bestimmtheitsmaß: Was uns R-Quadrat sagt

Stell dir vor, du versuchst, die Prüfungsnote von jemandem vorherzusagen, indem du schaust, wie viele Stunden er gelernt hat. Und, wie gut passt deine Vorhersage zu den tatsächlichen Ergebnissen? Das sagt uns der Bestimmtheitsmaß, auch^R² (R-Quadrat) genannt.

Es zeigt uns, wie viel von der Veränderung einer Sache (z. B. Prüfungsergebnisse) durch Veränderungen einer anderen Sache (z. B. Lernstunden) erklärt werden kann. So kannst du sehen, wie gut dein Modell zu den Daten passt.

In diesem Artikel erklären wir dir, was^R² bedeutet, warum es wichtig ist und wie du es berechnen und interpretieren kannst, auch wenn du noch keine Erfahrung mit Statistik hast. 

Was ist der Bestimmtheitsmaß?

Der Bestimmtheitsmaß, meistens als^R² (R-Quadrat) geschrieben, ist eine Zahl, die uns sagt, wie gut ein Regressionsmodell die Daten erklärt. Es zeigt, wie viel der Veränderung im Ergebnis (abhängige Variable) durch die Faktoren erklärt werden kann, die wir zur Vorhersage verwenden (unabhängige Variable(n)). 

Angenommen, du willst das Gewicht einer Person anhand ihrer Größe schätzen. Wenn^R² nahe bei 1 liegt, ist deine Vorhersage ziemlich gut. Die meisten Gewichtsunterschiede sind einfach auf unterschiedliche Körpergrößen zurückzuführen. Wenn^R² nahe bei 0 liegt, ist deine Vorhersage im Grunde genommen nur eine Vermutung, da in diesem Fall die Körpergröße die Gewichtsveränderung nicht wirklich erklärt.

Wir rechnen mit^R² -Werten zwischen 0 und 1:

• 0 heißt, dass das Modell die Variabilität in den Daten überhaupt nicht erklärt.

• 1 heißt, dass das Modell die ganze Variabilität erklärt.

• Werte näher an „ 1 “ bedeuten eine bessere Passung, was zeigt, dass dein Modell mehr Muster in den Daten erfasst.

Einfache lineare Regression

Wenn du nur mit einer unabhängigen Variablen arbeitest, wird das Modell als einfache lineare Regression bezeichnet. In diesem Fall hat^R² eine klare Beziehung zum Pearson-Korrelationskoeffizienten (r): R^² = r^²

Das heißt, wenn es eine starke positive oder negative Verbindung zwischen deinem Prädiktor und dem Ergebnis gibt, ist^R² hoch.

Hinweis: Bei Modellen mit mehr als einem Prädiktor (sogenannte multiple Regression) gibt^R² immer noch an, wie viel Varianz erklärt wird, aber es ist nicht mehr nur^r², da nun die Effekte mehrerer Variablen kombiniert werden.

Kann der Bestimmtheitsmaß negativ sein?

^R² ist normalerweise zwischen 0 und 1. Manchmal kann es aber auch vorkommen, dass du einen negativen R²-Wert siehst^. Das kann passieren, wenn:

• Dein Modell hat keinen Schnittpunkt (einen konstanten Startwert).
• Du benutzt das falsche Modell für die Daten.

Ein negativer^R²-Wert bedeutet, dass dein Modell schlechter abschneidet als eine einfache Durchschnittsprognose. Mit anderen Worten: Es passt so schlecht zu den Daten, dass es eigentlich irreführend ist.

Wie man den Bestimmtheitsmaß berechnet

Es gibt zwei gängige Methoden zur Berechnung von^R²:

1. Mit der Summe der Quadrate
2. Mit dem Korrelationskoeffizienten (r)

Schauen wir uns beides mal an.

Mit der Summe der Quadrate

Die gängigste Formel für^R² lautet:

Hier zeigt die Restquadratsumme (der nicht erklärte Teil), wie weit die tatsächlichen Werte von den Werten abweichen, die dein Modell vorhergesagt hat. Das ist der Fehler, den dein Modell macht.

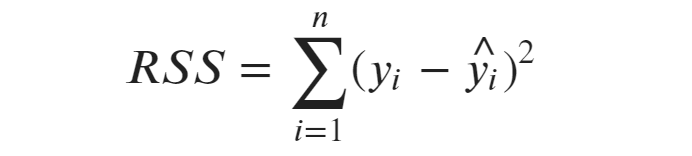
Die Summe der Quadrate ist die Gesamtabweichung der beobachteten Daten. Es zeigt uns, wie weit die tatsächlichen Werte vom Durchschnitt (Mittelwert) der abhängigen Variable entfernt sind.

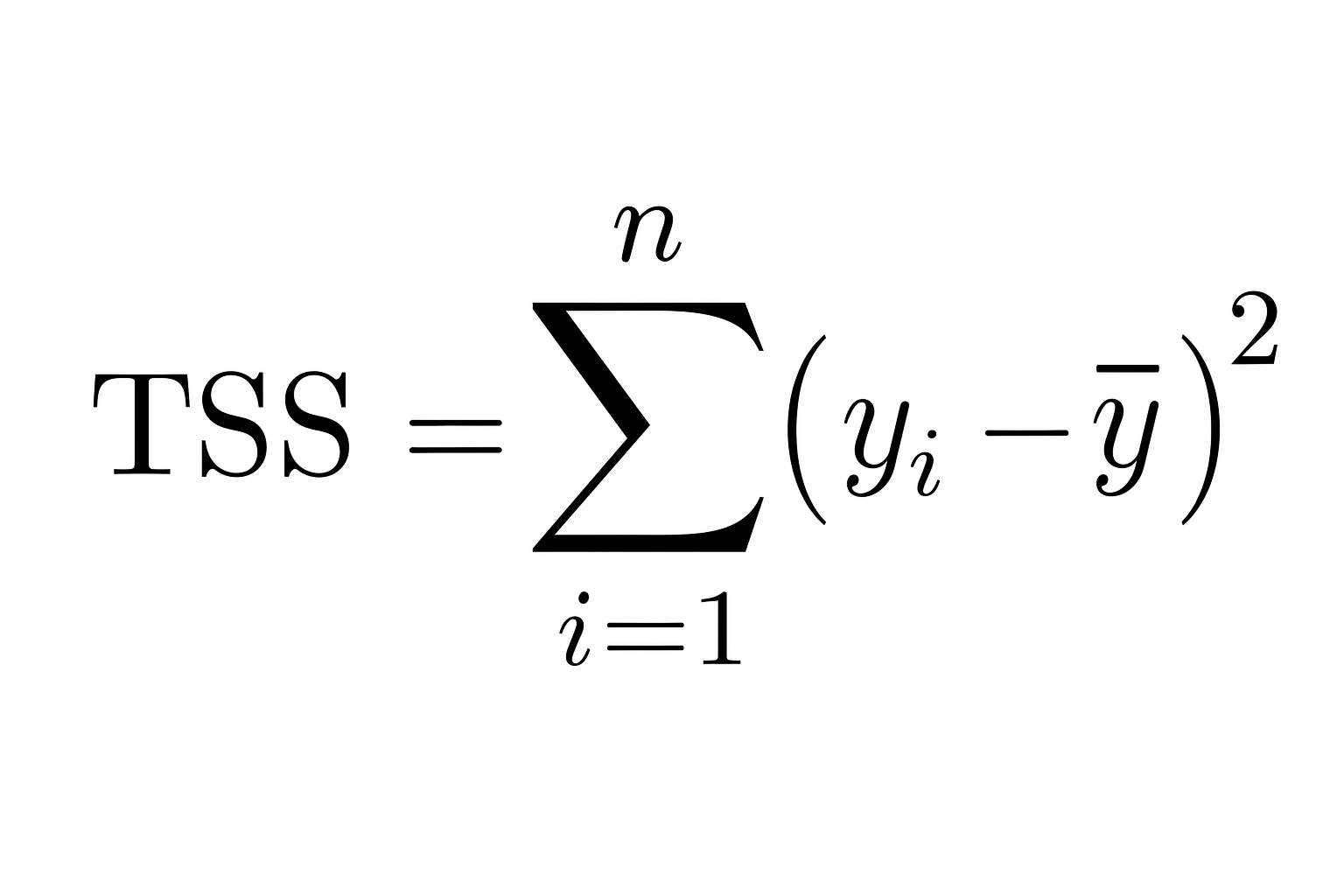
Je kleiner also die Summe der Restquadrate im Vergleich zur Summe der Quadrate ist, desto besser passt dein Modell zu den Daten und desto näher kommt^R² an den Wert 1.

Schauen wir uns das mal mit einem Beispiel an: 

Angenommen, du hast einen kleinen Datensatz mit folgenden Werten:

Berechne zuerst den Mittelwert der tatsächlichen Werte:

• y = (10+12+14)/3 = 12

Dann rechnest du die Summe der Quadrate (wie weit die tatsächlichen Werte vom Mittelwert entfernt sind):

• Summe der Quadrate insgesamt = (10 − 12)² + (12 − 12)² + (14 − 12)² = 4 + 0 + 4 = 8

Berechne dann die Restquadratsumme (wie weit die tatsächlichen Werte von den vorhergesagten Werten abweichen):

• Restquadratsumme = (10 − 12)² + (12 − 11)² + (14 − 13)² = 4 + 1 + 1 = 6

Jetzt füge das zur Formel hinzu:

• ^R² = 1 − ( Restquadratsumme / Gesamtsumme der Quadrate) = 1 − (6/8) = 1 − 0,75 = 0,25

Also,^R² = 0,25, was bedeutet, dass das Modell 25 % der Abweichungen in den Daten erklärt.

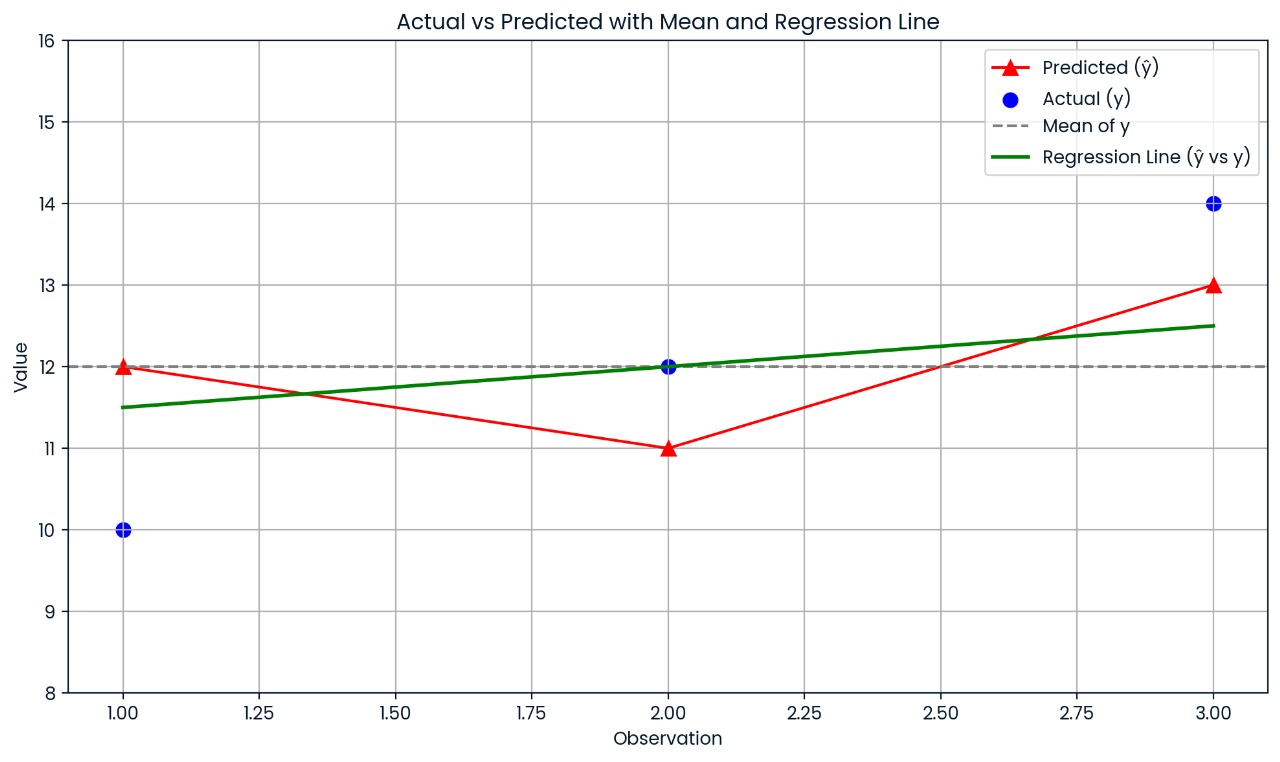
Diese Grafik zeigt, wie weit jeder tatsächliche Wert vom vorhergesagten Wert entfernt ist. Die Vorhersagen des Modells sind ziemlich daneben, deshalb ist R² nur 0,25; nur 25 % der Abweichungen werden erklärt.

Mit dem Korrelationskoeffizienten

Wenn du eine einfache lineare Regression (nur eine unabhängige Variable) verwendest, nimm diese Formel:

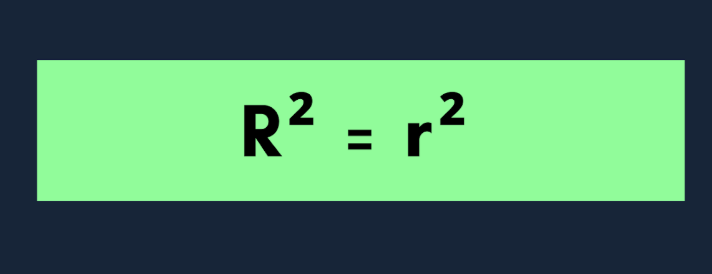
Hier ist r der Pearson-Korrelationskoeffizient zwischen den tatsächlichen und den vorhergesagten Werten. Diese Abkürzung klappt nur, wenn es nur einen Prädiktor gibt.

Nehmen wir mal an, die Korrelation zwischen X und Y ist: r = −0,8

Auch wenn die Korrelation negativ ist (was bedeutet, dass sich die Variablen in entgegengesetzte Richtungen bewegen), ist^R² positiv: ^R² = (−0,8)^² = 0,64

Also, 64 % der Abweichung im Ergebnis kann immer noch durch den Prädiktor erklärt werden, auch wenn die Beziehung negativ ist. Deshalb ist^R² immer positiv oder null; es zeigt, wie viel der Abweichung erklärt wird, nicht in welche Richtung.

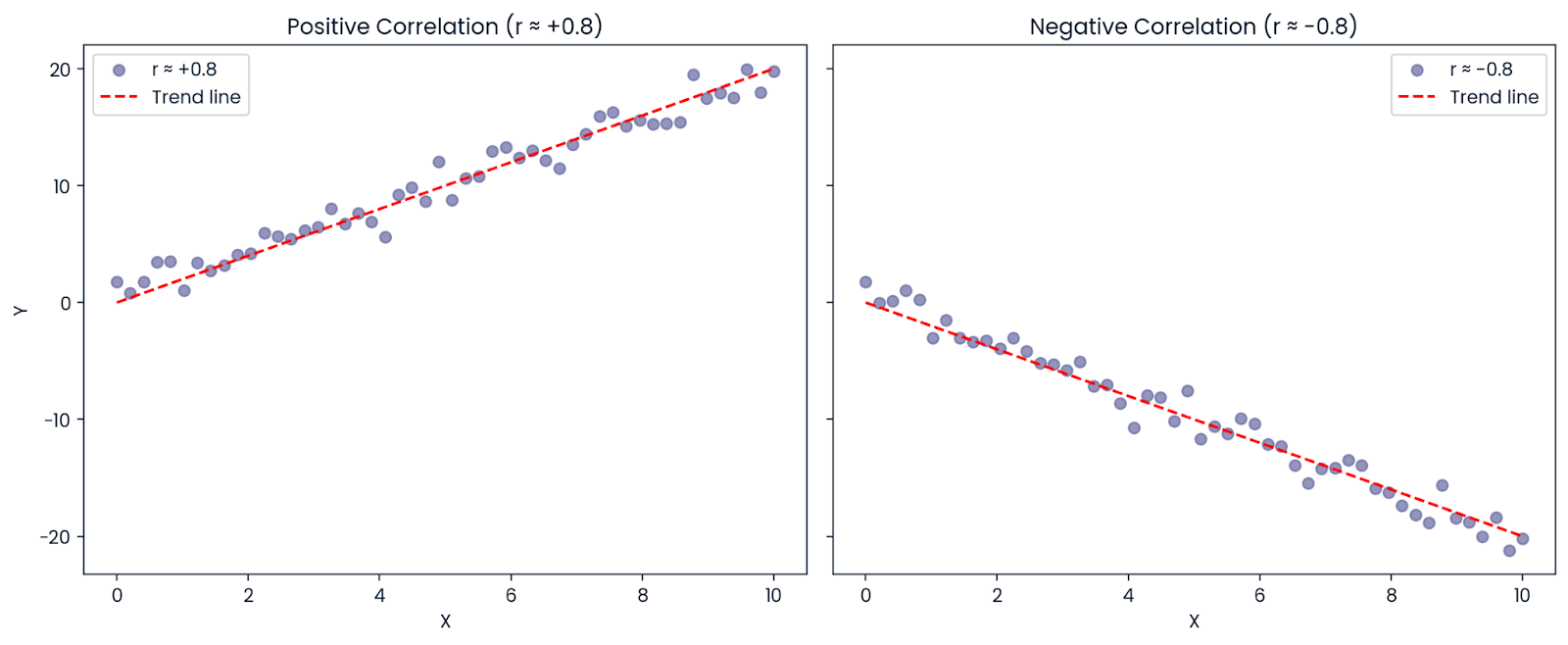
Positive und negative Korrelation. Bild vom Autor.

Wie man den Bestimmtheitsmaß interpretiert

Der Bestimmtheitsmaß sagt uns, wie viel der Abweichung im Ergebnis (abhängige Variable) durch unser Modell erklärt wird. Einfach gesagt, ist es wie die Frage: „Wie viel von den Veränderungen, die ich vorhersagen will, kann ich mit den Daten erklären, die ich benutze?“

Nehmen wir mal an, du baust ein Modell, um die Prüfungsergebnisse von Schülern vorherzusagen, je nachdem, wie viele Stunden sie lernen. Wenn dein Modell dir Folgendes anzeigt: ^R² = 0,90

Das heißt, dass 90 % der Unterschiede in den Prüfungsergebnissen durch unterschiedliche Lernzeiten erklärt werden können. Die restlichen 10 % kommen von anderen Sachen, die dein Modell nicht berücksichtigt hat, wie Schlaf, natürliche Begabung, Vorwissen oder wie schwer der Test war.

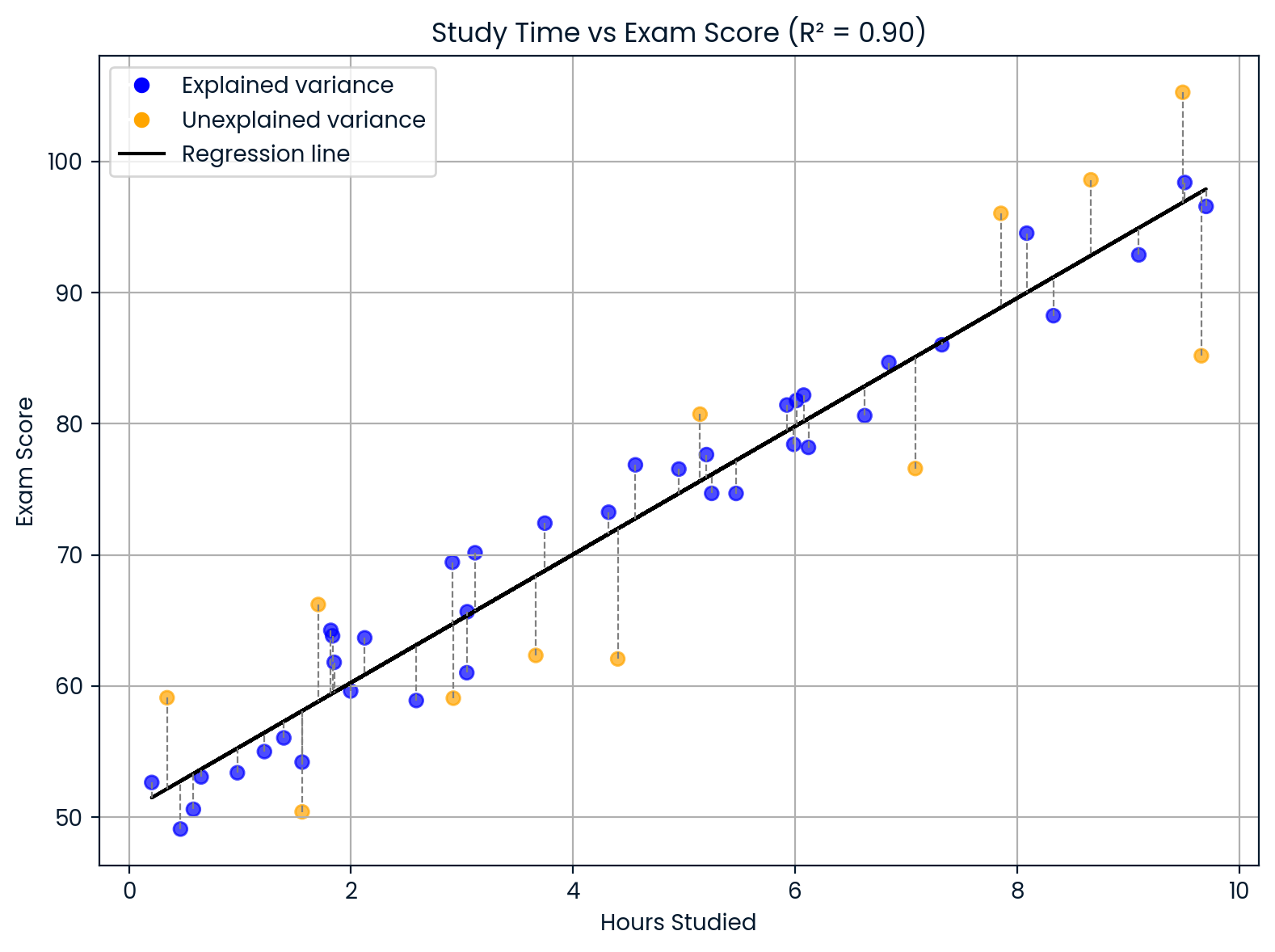
Den Bestimmtheitsmaß interpretieren. Bild vom Autor.

Diese Grafik zeigt, wie sich die Lernzeit auf die Prüfungsergebnisse auswirkt. 

• Die schwarze Linie zeigt, was das Modell sagt. 
• Die blauen Punkte zeigen, wie gut das Modell die Ergebnisse anhand der Lernzeit erklären konnte. 
• Orange Punkte zeigen Ergebnisse an, die nicht passen, wahrscheinlich wegen anderer Sachen wie Schlaf, Schwierigkeit des Tests oder dem Vorwissen des Schülers. Da^R² = 0,90 ist, passen die meisten Werte ins Schema, aber nicht alle.

Cohens Richtlinien

Jacob Cohen hat einen super nützlichen Leitfaden erstellt, der uns hilft zu verstehen, was verschiedene^R²-Werte bedeuten können, wenn wir die Stärke einer Beziehung einschätzen wollen.

Hier sind Cohens grobe Richtwerte für^R²:

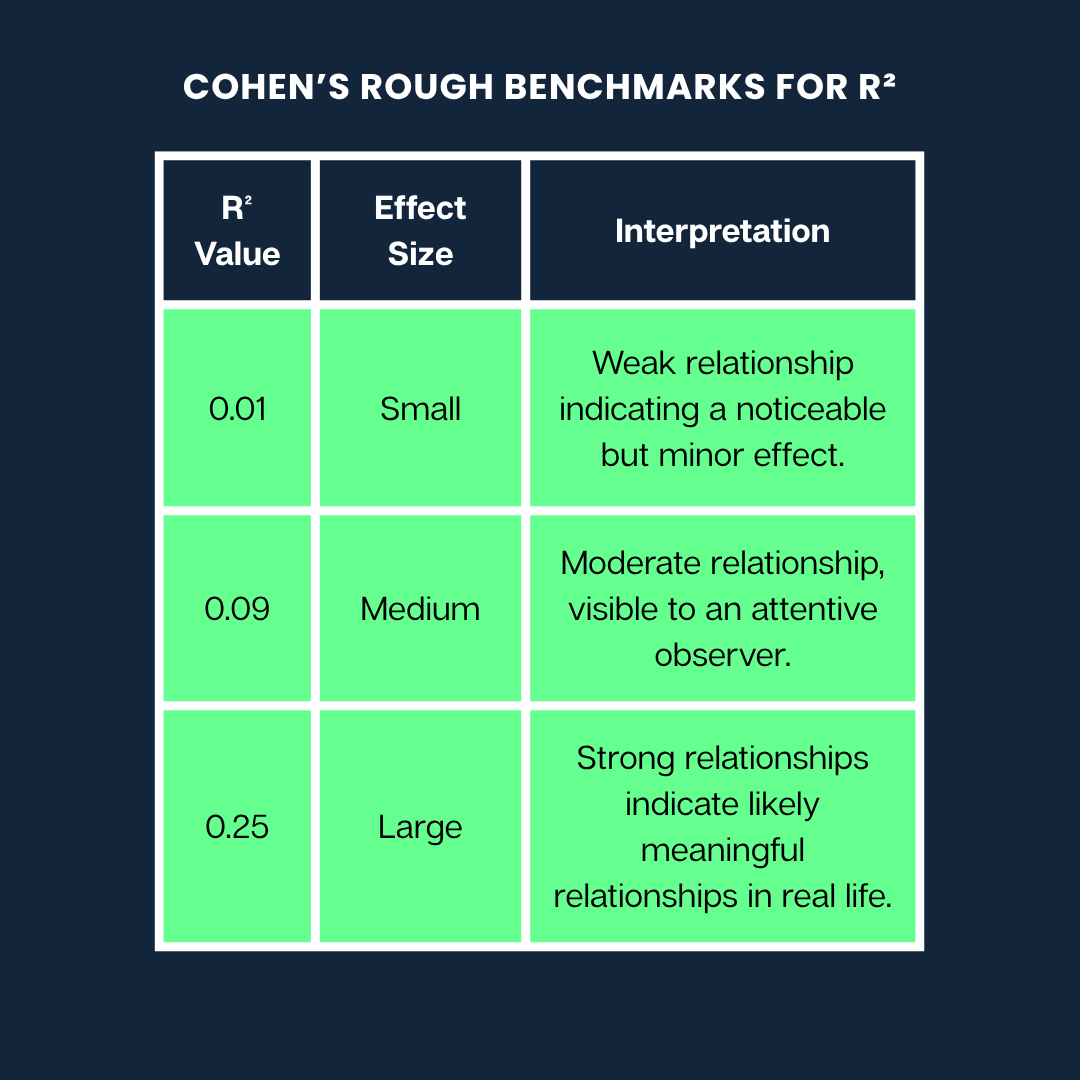
Cohens grobe Richtwerte. Bild vom Autor

Hinweis: Das sind nur ein paar allgemeine Tipps. Was als „großer“ oder „kleiner“ Effekt gilt, kann je nach Fachgebiet (z. B. Psychologie vs. Ingenieurwesen) und dem Kontext der Forschung stark variieren.

Einschränkungen und häufige Missverständnisse

^R² ist zwar hilfreich, aber du musst wissen, was es dir sagen kann und was nicht. Hier sind ein paar häufige Missverständnisse und Einschränkungen, auf die du achten solltest:

Mythos 1: Ein hoher Bestimmtheitsmaß bedeutet, dass das Modell besser passt.

Es mag so aussehen, als würde ein höherer^R²-Wert immer ein besseres Modell bedeuten, aber das ist nicht unbedingt der Fall. ^R² wird immer größer oder bleibt gleich, wenn du mehr Variablen zu einem Modell hinzufügst, auch wenn diese Variablen überhaupt nichts damit zu tun haben. 

Warum? 

Weil das Modell flexibler ist, um sich an die Trainingsdaten anzupassen, selbst wenn es nur zufälliges Rauschen passt. Das kann zu Überanpassung führen, wo dein Modell auf den Daten, mit denen es trainiert wurde, super aussieht, aber bei neuen Daten schlecht abschneidet.

Tipp: Ut das bereinigte R² beim Vergleich von Modellen mit unterschiedlicher Anzahl von Prädiktoren. Es bestraft unnötige Komplexität und kann dabei helfen, Überanpassung zu erkennen. 

Mythos 2: Ein hoher Bestimmtheitsmaß bedeutet, dass man neue Daten oder Ursachen ziemlich genau vorhersagen kann.

^R² misst nur, wie gut das Modell die Daten beschreibt, die du schon hast. Es sagt dir nicht:

• Wenn das Modell gute Vorhersagen für neue Daten macht
• Ob eine Variable die andere verursacht

Ein hoher^R²-Wert kann sogar zufällig entstehen, wenn du viele Prädiktoren verwendest. Schau dir also immer auch andere Metriken zur Modellbewertung an (wie RMSE oder MAE für die Vorhersagequalität) und denk dran: Korrelation ist nicht gleich Kausalität.

Mythos 3: Ein niedriger R-Quadrat-Wert bedeutet, dass das Modell nicht so toll ist.

Manchmal ist in komplizierten Systemen (wie bei der Vorhersage von menschlichem Verhalten oder Finanzmärkten) ein niedriger^R²-Wert zu erwarten.

Wenn du zum Beispiel etwas modellierst, das von vielen unvorhersehbaren oder nicht messbaren Faktoren beeinflusst wird, kann dein Modell trotzdem nützlich sein, auch wenn der^R²-Wert niedrig ist^. Es könnte einen wichtigen Trend zeigen oder Einblicke geben, auch wenn es nicht den Großteil der Abweichungen erklärt.

In der medizinischen oder psychologischen Forschung sind niedrige^R²-Werte ganz normal, weil die Ergebnisse bei Menschen von so vielen Variablen abhängen, die sich gegenseitig beeinflussen.

Andere Varianten: Partielles R-Quadrat und Verallgemeinerungen

Während^R² dabei hilft, zu verstehen, wie gut das Modell in die lineare Regression passt, gibt es noch andere Varianten und Verallgemeinerungen, die in anderen Modellierungskontexten nützlich sind.

Angepasster R-Quadrat-Wert

Genau wie der normale^R²-Wert zeigt uns^der angepasste^R²-Wert, wie viel der Abweichung in der abhängigen Variable durch das Modell erklärt wird. Aber es geht noch einen Schritt weiter, indem es unnötige Komplexität bestraft. Mit anderen Worten: Es hält dich davon ab, dein Modell mit zusätzlichen Prädiktoren zu überladen, die nicht weiterhelfen.

Die Formel lautet:

Adjusted R² = 1 - [ (1 - R²) × (n - 1) / (n - p - 1) ]

Hier:

• n ist die Anzahl der Beobachtungen (Datenpunkte)

• p ist die Anzahl der Prädiktoren (unabhängige Variablen)

Die Formel passt^R² nach unten an, wenn eine neue Variable das Modell nicht verbessert. Diese Strafe wird stärker, je mehr Prädiktoren du hinzufügst.

Wenn du zum Beispiel eine neue Variable hinzufügst, die die Genauigkeit deines Modells verbessert, steigt^der angepasste^R²-Wert. Aber wenn diese Variable kaum was ändert oder nur zufällig hilft, geht^der angepasste^R² runter und zeigt dir, dass es vielleicht eine Überanpassung gibt.

Das macht^das bereinigte^R² super zum Vergleichen von Modellen.

Nehmen wir mal an, du willst zwischen einem einfacheren Modell mit drei Prädiktoren und einem komplexeren mit sechs Prädiktoren wählen. Selbst wenn das komplexe Modell einen etwas höheren^R²-Wert hat, kann der angepasste^R²-Wert niedriger sein, was bedeutet, dass sich die zusätzliche Komplexität nicht lohnt.

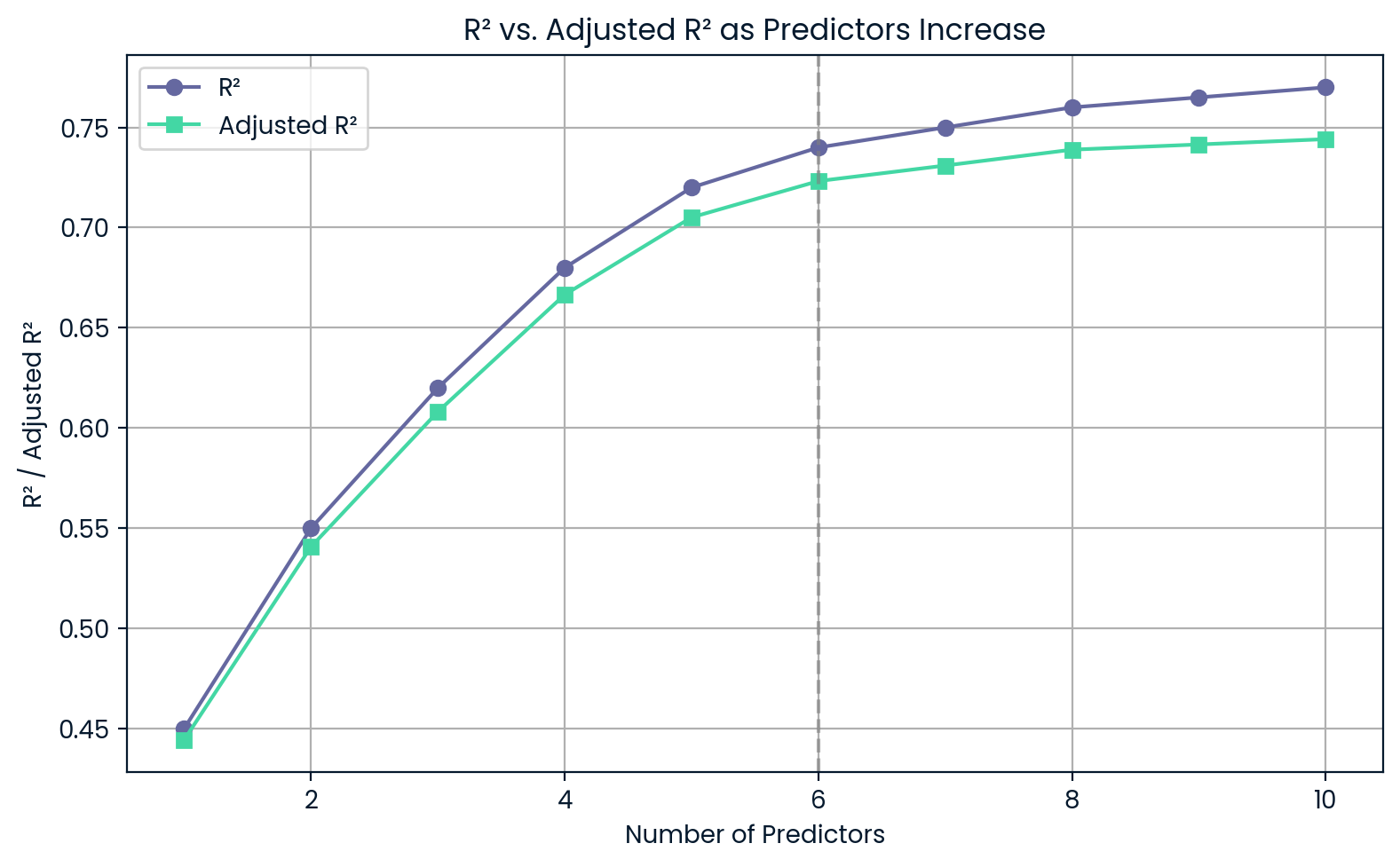
R² im Vergleich zu bereinigtem R², wenn die Prädiktoren zunehmen. Bild vom Autor.

Dieses Diagramm zeigt, dass mit jedem neuen Prädiktor^{der R²-Wert} weiter steigt, auch wenn die Prädiktoren nicht besonders nützlich sind. Andererseits sinkt^der bereinigte^R²-Wert, wenn du zu viel hinzufügst, was dich vor einer Überanpassung warnt.

Partialer Bestimmtheitsmaß

^Der partielle^R² (oder partielle Bestimmungskoeffizient) zeigt, wie viel zusätzliche Varianz in der abhängigen Variable erklärt wird, wenn man einen bestimmten Prädiktor zu einem Modell hinzufügt, das schon andere enthält.

Um^das partielle^R² zu berechnen, vergleichen wir zwei Modelle:

• Das reduzierte Modell, das den fraglichen Prädiktor rauslässt
• Das komplette Modell, das alle Prädiktoren enthält

Die Formel für^das partielle^R² basiert auf der Verringerung der Summe der quadrierten Fehler (SSE), wenn die neue Variable hinzugefügt wird. Eine gängige Form ist:

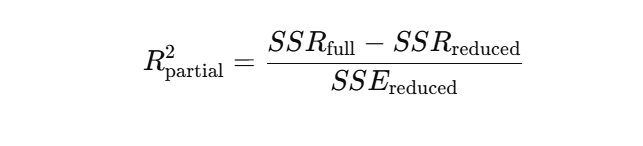
Oder in Form von Regressionsquadratsommen:

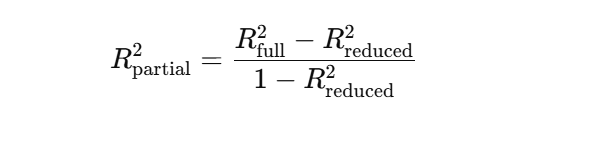
Angenommen, du baust ein Modell, um Produktverkäufe vorherzusagen. 

Du hast bereits „Produktpreis“ und „Saison“ im Modell. Jetzt willst du sehen, ob die Vorhersagen besser werden, wenn du „Marketingausgaben“ hinzufügst. Der partielle R²-Wert zeigt dir, wie viel mehr Abweichungen bei den Verkäufen durch die Berücksichtigung der „Marketingausgaben“ erklärt werden können.

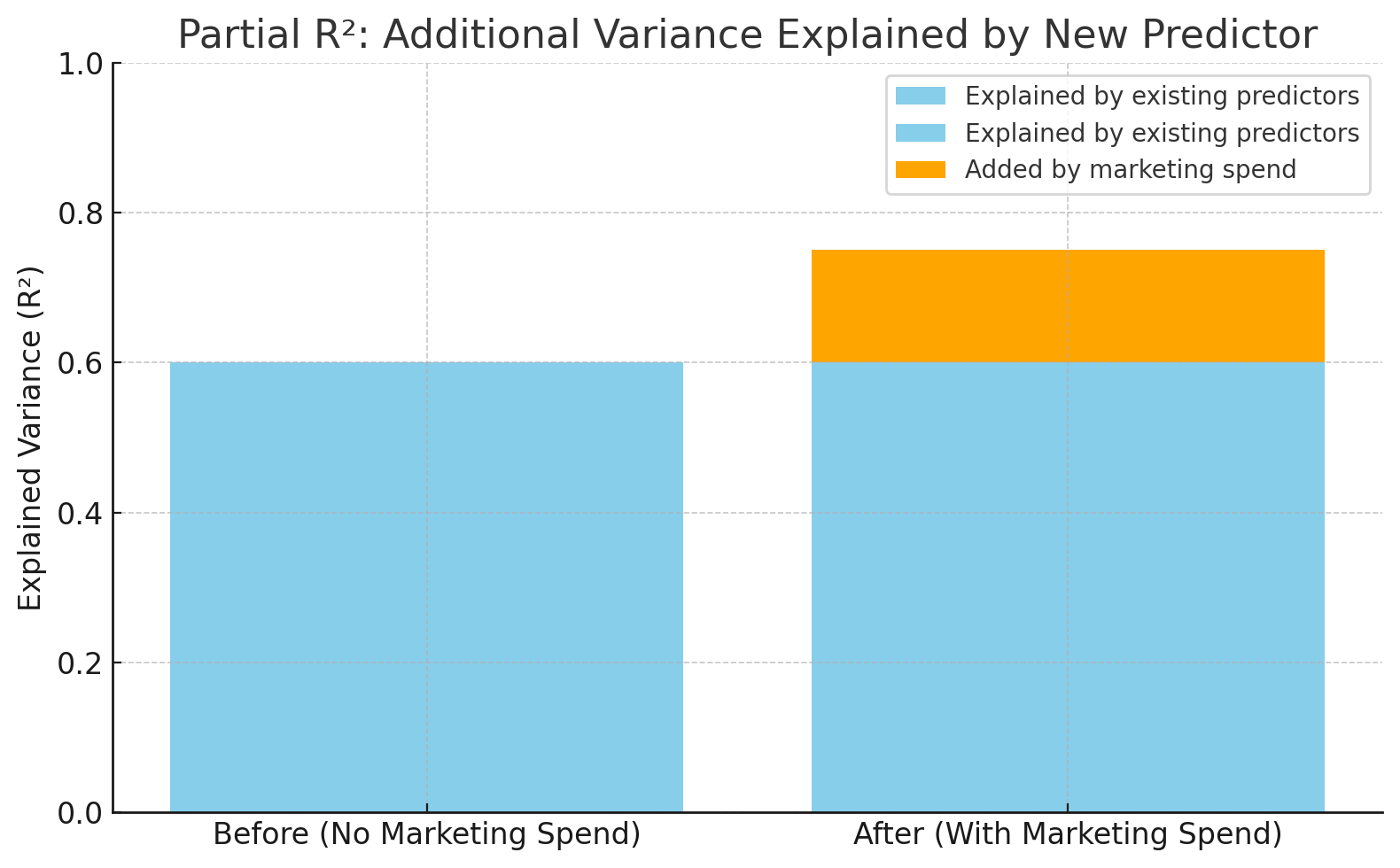
^R² stieg nach Hinzufügen der Marketingausgaben von 0,60 auf 0,75. Bild vom Autor.

Diese Grafik zeigt, wie viel genauer das Modell wird, wenn „Marketingausgaben“ dazugerechnet werden. ^R² geht von 0,60 auf 0,75, was bedeutet, dass die neue Variable 15 % mehr der Abweichungen im Umsatz erklärt – das ist der partielle^R².

Bestimmtheitsmaß in der logistischen Regression

Bei der logistischen Regression ist die Ergebnisvariable kategorisch, wie z. B. ja/nein, bestanden/nicht bestanden, sodass^das traditionelle^R² nicht passt. Stattdessen verwenden wir^Pseudo-R² -Metriken, die einen ähnlichen Zweck erfüllen: Sie zeigen an, wie gut das Modell die Abweichungen in den Ergebnissen erklärt.

Zwei gängige^Pseudo-R² -Werte sind:

• Cox & Snell^R²: Die Schätzungen erklären die Varianz, aber ihr Maximalwert ist selbst bei einem perfekten Modell kleiner als 1.
• Nagelkerke R^²: Eine korrigierte Version von Cox & Snell^R², die bis 1 skaliert und dadurch einfacher zu interpretieren ist als das traditionelle R^².

Angenommen, du modellierst, ob ein Kunde auf eine Anzeige klicken wird (ja/nein). Da das Ergebnis binär ist, kannst du nicht das normale R² nehmen^. Aber^Pseudo-R² -Werte wie Nagelkerke helfen dabei, logistische Modelle zu vergleichen und ihre Vorhersagekraft zu beurteilen, auch wenn sie nicht direkt mit^R² in der linearen Regression gleichzusetzen sind.

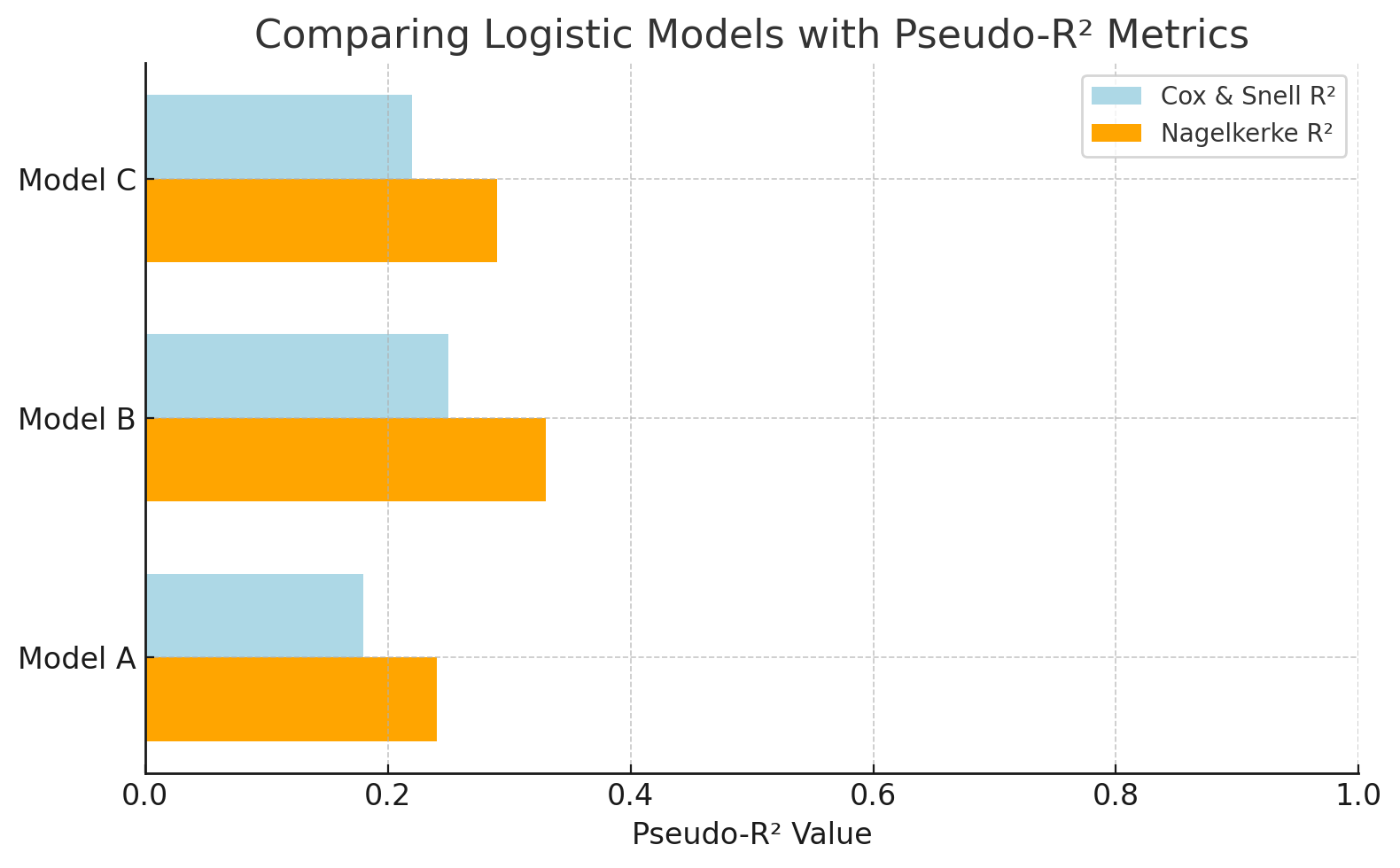
Logistikmodelle mit^Pseudo-R² -Metriken vergleichen. Bild vom Autor.

Dieses Diagramm vergleicht logistische Regressionsmodelle anhand von^Pseudo-R² -Werten. Nagelkerke^R² ist eine besser zu verstehende Skala als Cox & Snell. So kann man besser einschätzen, wie gut jedes Modell das Ergebnis erklärt (z. B. die Vorhersage von Klicks auf Anzeigen).

Bestimmungskoeffizient im Vergleich zu anderen Modellanpassungsmetriken

^R² ist zwar hilfreich, um zu verstehen, wie viel Abweichung erklärt wird, aber es zeigt nicht, wie weit deine Vorhersagen daneben liegen. Dafür gibt's fehlerbasierte Kennzahlen wie RMSE, MAE und MAPE.

Hier ein kurzer Vergleich:

Praktische Anwendungen in verschiedenen Bereichen

Schauen wir uns jetzt mal ein paar der vielen Fälle an, in denen der Bestimmtheitsmaß verwendet wurde. 

Wirtschaft: Erklärung der Schwankungen des BIP

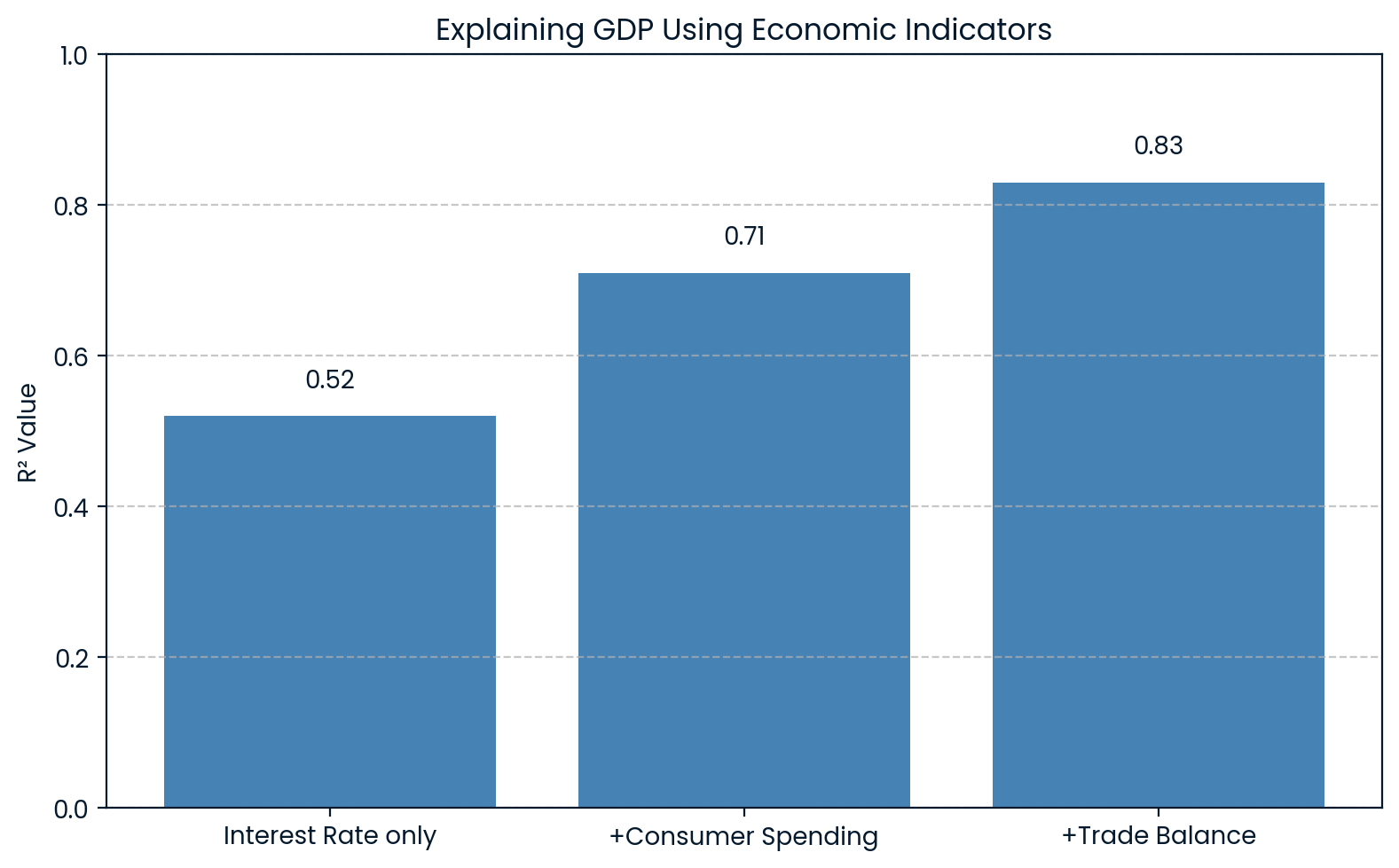
In der Wirtschaft wird^R² benutzt, um Veränderungen bei großen Indikatoren wie dem Bruttoinlandsprodukt (BIP) zu erklären. Ein Modell kann zum Beispiel Variablen wie Zinssätze, Konsumausgaben und Handelsbilanzen enthalten, um das BIP vorherzusagen.

0.83Wenn so ein Modell einen^R²-Wert von 0,83 zurückgibt, heißt das, dass 83 % der Schwankungen im BIP durch diese wirtschaftlichen Faktoren erklärt werden können. Das hilft Ökonomen zu verstehen, wie viel von den Schwankungen des BIP auf bekannte Faktoren zurückzuführen sind.

Eine Studie von „ ” hat Daten aus den USA verwendet. BIP- en als unabhängige Variable zur Vorhersage des S&P 500 Index und fanden einen^R²-Wert von 0.83. Das hat gezeigt, dass es einen starken Zusammenhang zwischen der Wirtschaft und den Entwicklungen an der Börse gibt.

^R² erklärt die Wirtschaft des BIP. Bild vom Autor.

Die Grafik zeigt, dass mit jedem neuen Wirtschaftsindikator, der zum Modell hinzugefügt wird, der^R²-Wert steigt, von 0.52 auf 0.83 mit allen drei Variablen. Das zeigt, dass jeder zusätzliche Faktor die Schwankungen des BIP besser erklärt.

Finanzen: Aktienkursentwicklung im Vergleich zum Marktindex

In der Finanzwelt wird^R² benutzt, um zu messen, wie sehr die Rendite einer Aktie durch die allgemeinen Marktbewegungen erklärt werden kann. Dazu werden die Renditen einer Aktie mit einem Marktindex wie dem S&P 500 verglichen.

0.82Wenn du zum Beispiel die Rendite von Apple (AAPL) mit dem S&P 500 vergleichst und^R² = 0,85 bekommst, heißt das, dass 85 % der Renditebewegungen von Apple durch den breiteren Markt erklärt werden können.

• Ein hoher^R²-Wert zeigt, dass die Aktie eng mit dem Markt verbunden ist.
• Ein niedriger^R²-Wert bedeutet, dass die Aktie unabhängiger ist.

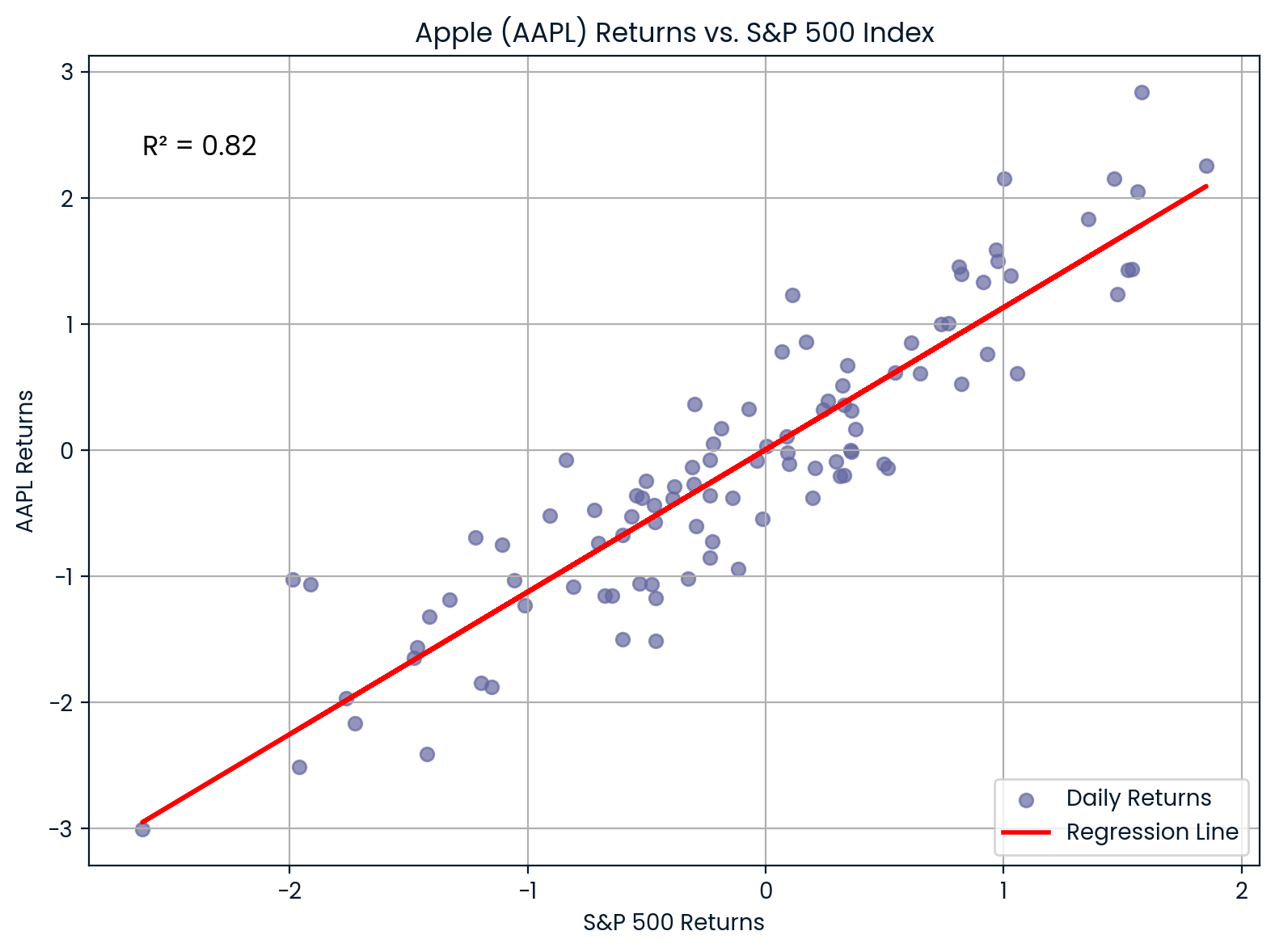
Zusammenhang zwischen AAPL und S&P 500. Bild vom Autor.

Die Grafik zeigt, wie stark Apple (AAPL) und der S&P 500 zusammenhängen. 0.82Mit einem^R² von 0,999999999999999999999999999999999999999999999999999999

Marketing: Werbeausgaben und Conversions

Im Marketing zeigt^R², wie gut die Ausgaben für Werbung die Konversionsraten der Kunden erklären.

Angenommen, du arbeitest bei einem E-Commerce-Unternehmen und möchtest wissen, ob eine Erhöhung der monatlichen Werbeausgaben die Conversion-Raten verbessert. Du machst eine lineare Regression und bekommst^R² = 0,98. Das heißt, dass 98 % der Schwankungen in der Conversion-Rate durch deine Werbeausgaben erklärt werden können, was auf einen ziemlich starken Zusammenhang hindeutet.

Diese Einblicke helfen Marketingfachleuten dabei:

• Prognose der Umwandlungsergebnisse
• Werbebudgets rechtfertigen
• Den Return on Investment (ROI) einschätzen

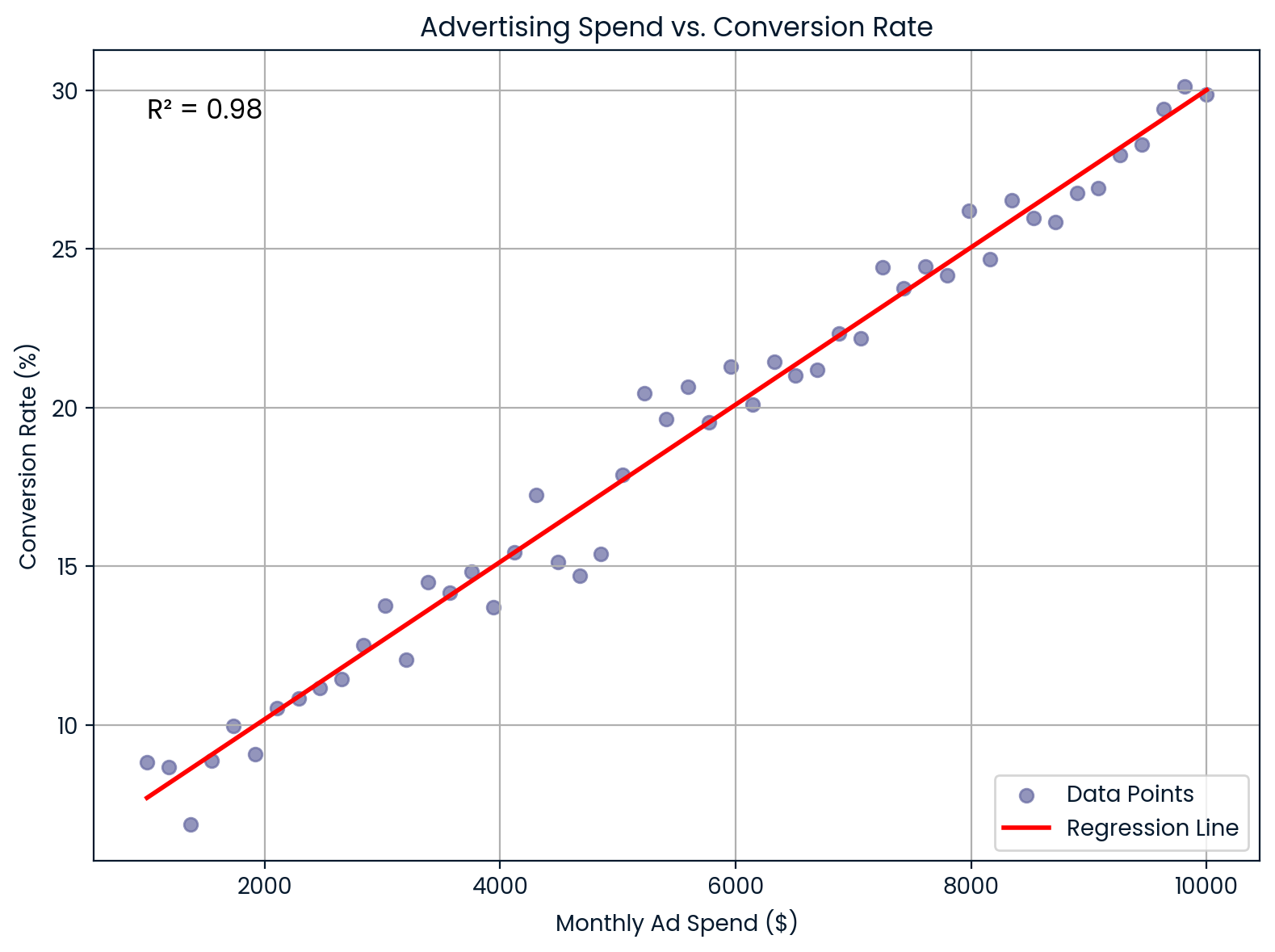
Monatliche Werbeausgaben im Vergleich zur Conversion-Rate. Bild vom Autor.

Dieses Diagramm zeigt eine fast perfekte lineare Beziehung zwischen den monatlichen Werbeausgaben und der Konversionsrate. Es hilft dabei, den ROI und das Budget ziemlich gut vorherzusagen.

Maschinelles Lernen: Bewertung von Regressionsmodellen

Beim maschinellen Lernen wird^R² als Leistungsmaß für Regressionsaufgaben verwendet. Bibliotheken wie scikit-learn haben die Funktion „ r2_score() ”, um das zu berechnen.

Es zeigt dir, wie gut dein Modell die Schwankungen in den Daten erklärt:

• ^R² nahe bei 0, 1 bedeutet, dass die Anpassung gut ist und es kaum Fehler gibt.

• ^R² nahe 0 bedeutet schlechte Passung

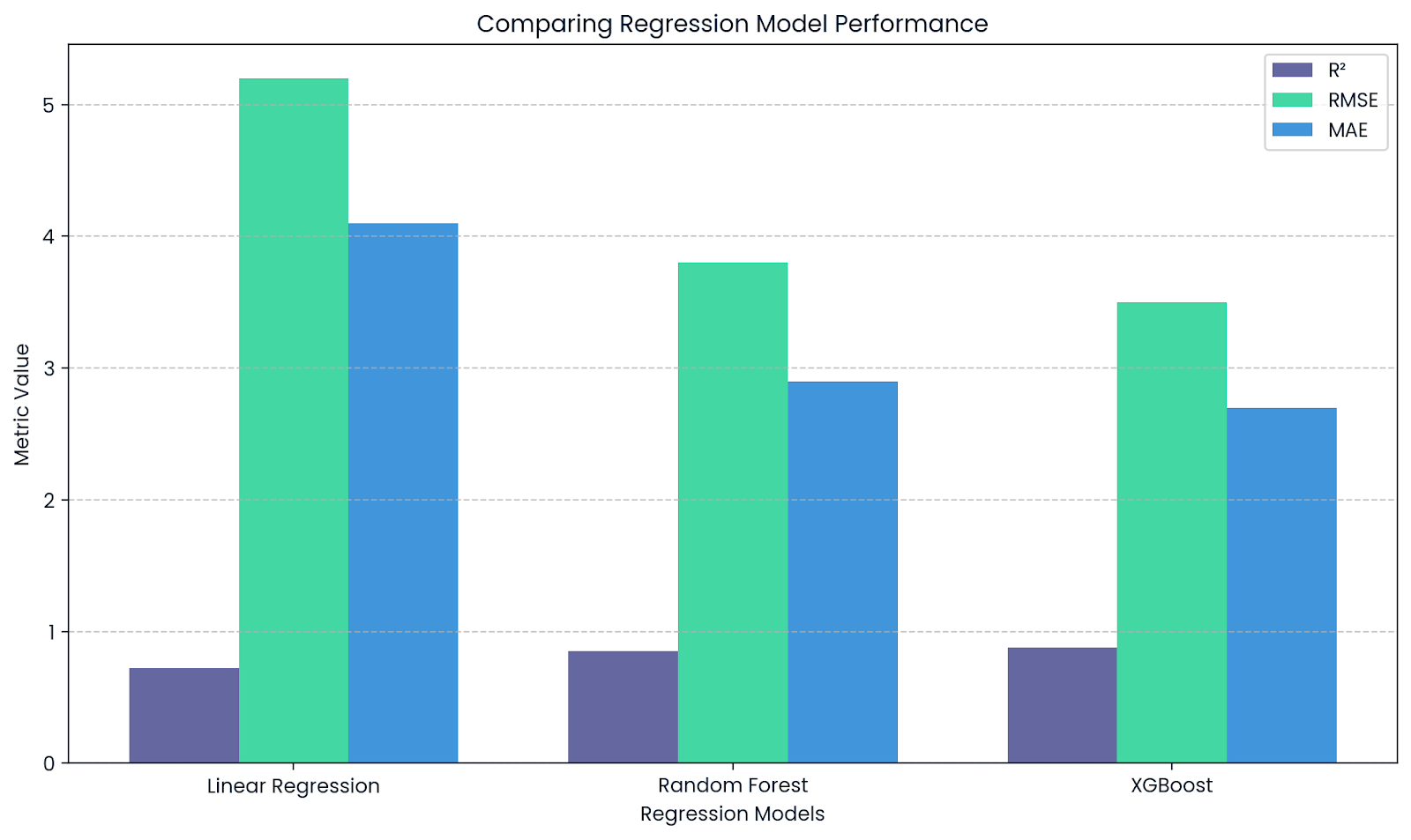
^R² ergänzt RMSE und MAE. Bild vom Autor.

Diese Grafik zeigt, wie R² andere Kennzahlen wie RMSE und MAE bei der Bewertung von Regressionsmodellen ergänzt. Während^R² die Erklärungskraft zeigt, geben RMSE und MAE einen Einblick in die tatsächliche Größe der Vorhersagefehler.

Den Bestimmungskoeffizienten in der Forschung angeben

Wenn du^R² in einer Forschungsarbeit oder einem Projekt verwendest, solltest du ein paar Formatierungsregeln beachten:

• Achte darauf, dass du^R² kursiv schreibst, und ja, es sollte ein großes R sein, kein kleines. 
• Schreib keine führende Null vor die Dezimalstelle. Also schreib nicht^R² = 0,73, sondern^R² = 0,73. Und wenn du nicht wirklich mehr Details brauchst, runde auf zwei Dezimalstellen.

Wenn du^R² in einer Regressionsanalyse oder ANOVA verwendest und testest, ob dein Modell signifikant ist, solltest du noch ein paar weitere Angaben machen: die F-Statistik, die Freiheitsgrade und den p-Wert. Diese sagen dem Leser, wie sicher wir uns sein können, dass dein Modell etwas Sinnvolles erklärt.

Wenn du also Ergebnisse berichtest, könnte das etwa so aussehen:

„Das Modell erklärt einen großen Teil der Abweichungen bei den Verkäufen,^R² = 0,73, F(2, 97) = 25,42, p < 0,001.“

Wenn du aber keinen Hypothesentest machst, sondern eine explorative Analyse durchführst oder die Leistung eines Modells mit Kreuzvalidierung bewertest, kannst du den R²-Wert einfach so angeben.

Der Bestimmtheitsmaß in Python, R und Excel

Schauen wir mal, wie man^R² auf drei verschiedene Arten berechnen kann: Python, R und Excel in einem kleinen Projekt, wo wir die Noten von Schülern anhand ihrer Lernzeit vorhersagen.

Wir werden für alle drei Beispiele den folgenden Datensatz verwenden:

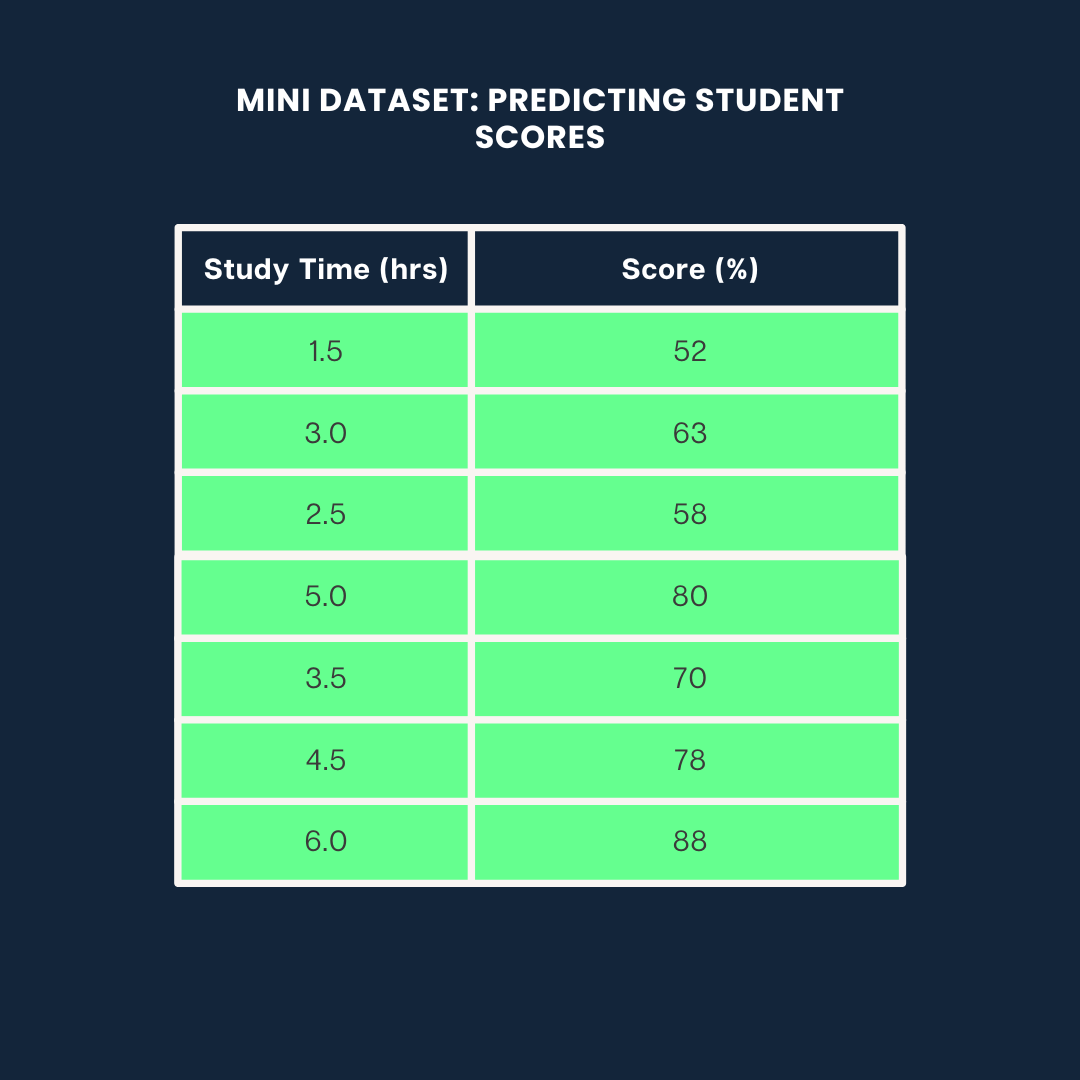
Beispiel-Datensatz. Bild vom Autor

Bestimmungskoeffizient in Python

So berechnest du^R² in Python mit „ scikit-learn “:

from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
import numpy as np

# Data
study_time = np.array([1.5, 3.0, 2.5, 5.0, 3.5, 4.5, 6.0]).reshape(-1, 1)
scores = np.array([52, 63, 58, 80, 70, 78, 88])

# Model
model = LinearRegression()
model.fit(study_time, scores)
predicted_scores = model.predict(study_time)

# R² score
r2 = r2_score(scores, predicted_scores)
print(f"R² = {r2:.2f}")

0.99

Das heißt, dass 99 % der Unterschiede in den Ergebnissen durch die Lernzeit erklärt werden können.

Wenn du mehr über Regressions- und Statistikmodelle erfahren möchtest, schau dir unseren Leitfaden „Einführung in die Regression mit statsmodels in Python“ an. 

Bestimmtheitsmaß in R

In R kannst du R² mit ein paar Zeilen über die Funktion „ lm() “ berechnen:

# Data
study_time <- c(1.5, 3.0, 2.5, 5.0, 3.5, 4.5, 6.0)
scores <- c(52, 63, 58, 80, 70, 78, 88)

# Linear model
model <- lm(scores ~ study_time)

# R-squared
summary(model)$r.squared

0.9884718

Ungefähr 98 % der Unterschiede in den Ergebnissen hängen von der Lernzeit ab. Wenn du mehr über Regression in R erfahren möchtest, schau dir unseren Kurs „Einführung in die Regression in R“ an.

Bestimmtheitsmaß in Excel

In Excel kannst du R² mit der eingebauten Funktion „ RSQ() “ berechnen. Angenommen:

• Die Lernzeit ist in den Zellen A2:A8

• Die Ergebnisse sind in den Zellen B2:B8

Die Syntax ist:

RSQ(known_y's,known_x's)

Ich hab die folgende Formel benutzt:

=RSQ(B2:B8,A2:A8)

Damit sagst du Excel, dass es den^R²-Wert zwischen der abhängigen Variable (Ergebnisse) und der unabhängigen Variable (Lernzeit) berechnen soll.

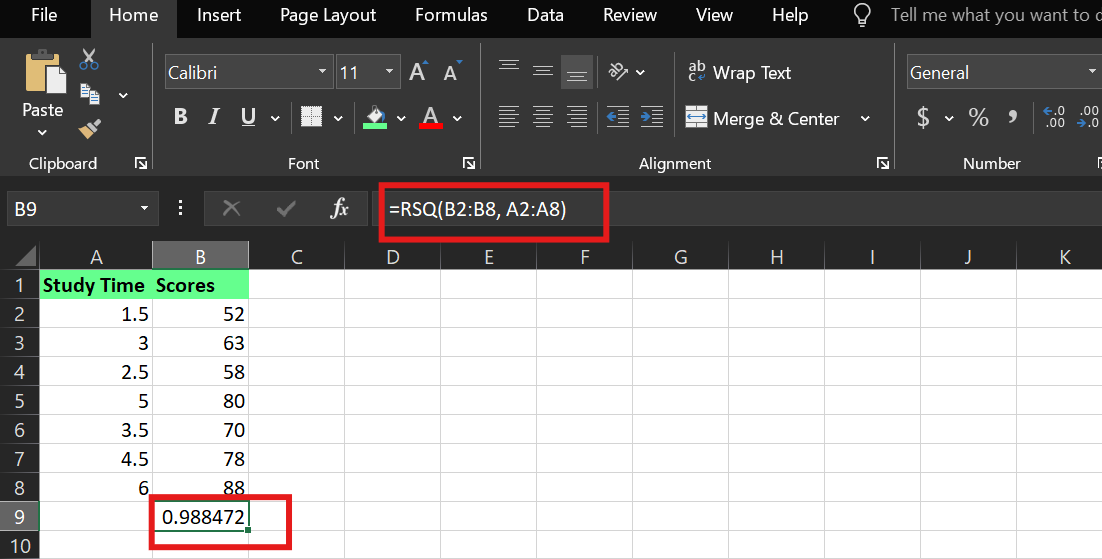
^R² -Beispiel in Excel. Bild vom Autor.  

Wichtigste Erkenntnisse

Egal, ob du Noten von Schülern, Aktienrenditen oder das Verhalten von Kunden vorhersagst – der Bestimmtheitsmaß sagt dir, wie viel von dem Ergebnis dein Modell wirklich versteht. 

Ein hoher Bestimmtheitsmaß kann echt beeindruckend aussehen, aber lass dich davon nicht täuschen und denk nicht, dass das Modell perfekt ist oder dass es Ursache und Wirkung beweist. Und ein niedriger Bestimmtheitsmaß bedeutet nicht immer, dass etwas nicht funktioniert. Es könnte auch bedeuten, dass dein System komplex ist oder deine Variablen nicht komplett sind.

Wenn du also Modelle erstellst oder analysierst, frag dich selbst:

• Was erkläre ich gut?
• Was übersehe ich hier?
• Und ist mein Modell nicht nur genau, sondern auch nützlich?

Wenn du mit dieser Einstellung startest, kannst du den Bestimmtheitsmaß als Hilfsmittel für bessere Entscheidungen nutzen.