Mean Shift Clustering: Ein umfassender Leitfaden
Clustering ist eine unbeaufsichtigte maschinelle Lerntechnik, die verborgene Strukturen in den Daten identifiziert, um Unternehmen zu helfen, fundiertere Entscheidungen zu treffen. Einige der gängigsten Clustering-Anwendungen sind Bildsegmentierung, Kundensegmentierung und die Analyse sozialer Netzwerke.
Je nachdem, ob der Algorithmus eine vorgegebene Anzahl von Clustern oder die Verteilung der Daten als Eingabe benötigt, gibt es zwei Arten von Clustern: parametrische und nicht-parametrische. In diesem Beitrag werden wir einen solchen nicht-parametrischen Algorithmus im Detail vorstellen: den Mean-Shift-Clustering-Algorithmus. Wir werden die zugrundeliegenden Prinzipien erörtern, ihre Anwendungen in verschiedenen Branchen untersuchen und eine Python-Implementierung vorstellen. Zum Schluss vergleichen wir sie mit der beliebten k-means Clustering-Technik.
Was ist Mean Shift Clustering?
Das Mean-Shift-Clustering wird zur Identifizierung von Clustern in Datensätzen verwendet, bei denen die Anzahl der Cluster im Voraus nicht bekannt ist. Es findet Cluster, indem es Datenpunkte iterativ in die dichtesten Regionen im Merkmalsraum verschiebt. Das macht sie besonders nützlich für Anwendungen wie die Objekterkennung, bei der sie Bilder anhand von Pixelintensität und Farbe segmentieren kann, und auch für die Verfolgung von Objekten in Videosequenzen.
Als modussuchender Algorithmus kennzeichnet er die Cluster, indem er die Modi oder Peaks in der Datenverteilung findet. Sie hebt im Wesentlichen die am dichtesten besiedelten Gebiete hervor. Dies geschieht, indem die Clusterzentren iterativ in Regionen mit höherer Datendichte verschoben werden. Hier sind die Schritte:
- Initialisierung: Beginne damit, jeden Datenpunkt als potenziellen Kandidaten für das Clusterzentrum zu betrachten.
- Density Estimation: Lege für jeden Datenpunkt ein Fenster um ihn herum fest, den sogenannten Radius, und berechne dann den Mittelwert der Datenpunkte innerhalb dieses Radius.
- Shifting: Verschiebe jeden Punkt zu dieser mittleren Position. Dieser Schritt verschiebt den Punkt in Richtung der Region mit höherer Dichte.
- Konvergenz: Wiederhole die Schritte 2 und 3 iterativ bis zur Konvergenz, d.h. wenn die Verschiebung kleiner als ein vordefinierter Schwellenwert ist. Die unbedeutende Veränderung der Verschiebung deutet darauf hin, dass sich die Punkte um die lokalen Maxima der Dichtefunktion stabilisiert haben.
Am Ende dieses iterativen Prozesses gruppieren sich die Datenpunkte um die Modi der Datenverteilung und bilden die Cluster. Die Mittelwertverschiebung ist besonders flexibel, weil sie sich auf die tatsächliche Verteilung der Daten stützt, anstatt eine vordefinierte Form für die Cluster anzunehmen, wodurch sie mit beliebig geformten Clustern umgehen kann.
Warum Mean Shift Clustering?
Das Mean-Shift-Clustering ist ein leistungsfähiges Instrument, um die zugrunde liegende Struktur von Daten aufzudecken, ohne Annahmen über ihre Parameter wie die Anzahl der Cluster oder ihre Form zu treffen. Der dichtebasierte Ansatz, der sich auf Regionen mit hoher Datendichte konzentriert, ist robust gegenüber Ausreißern und stellt sicher, dass verrauschte Daten nur minimale Auswirkungen auf den Clustering-Prozess haben. Diese Robustheit macht sie zu einer geeigneten Lösung für reale Datensätze, die oft Unregelmäßigkeiten und Rauschen enthalten, und für Anwendungen, die Anpassungsfähigkeit und Präzision erfordern.
Einige der realen Szenarien, in denen das Mean Shift Clustering gut funktioniert, sind:
Bildsegmentierung
Der Mean-Shift-Clustering-Algorithmus kann Bilder anhand der Pixelintensität oder der Farbe in Regionen unterteilen, ohne dass die Anzahl der Segmente vorher bekannt sein muss. Diese Flexibilität macht es für Bildsegmentierungsaufgaben sehr effektiv, da die mit Mean Shift Clustering erzeugten Cluster jede Form und Größe annehmen können.
Bildsegmentierung mit Mean Shift Clustering. Quelle: ResearchGate
Außerdem sind Bilder, die Rauschen enthalten, besonders bei schlechten Lichtverhältnissen, schwer zu segmentieren. Für solche Szenarien bietet der Mean-Shift-Clustering-Algorithmus eine natürlichere und genauere Segmentierung, die in Anwendungen wie der medizinischen Bildgebung zur Erkennung abnormaler Gewebetypen oder in der Computer Vision zur zuverlässigen Objekterkennung unerlässlich ist.
Objektverfolgung in der Videoanalyse
Aufgrund seiner Vorteile bei der Bildsegmentierung wird das Mean Shift Clustering häufig bei der Objektverfolgung in Videostreams eingesetzt. Seine Fähigkeit, Objekte dynamisch zu identifizieren und zu verfolgen, während sie sich über Frames hinweg bewegen, macht es sehr effektiv für Echtzeit-Tracking-Anwendungen.
Mean Shift Clustering bei der Objektverfolgung. Quelle: ResearchGate
Durch die Konzentration auf die Dichte von Pixeln oder Merkmalen, die mit dem Objekt verbunden sind, kann Mean Shift Objekte unterschiedlicher Form und Größe effektiv verfolgen und sich so leicht an Veränderungen in Bewegung und Aussehen anpassen.
Kundensegmentierung im Marketing
Für Unternehmen ist es wichtig, Kundensegmente zu verstehen, ohne von einer festen Anzahl von Kategorien auszugehen und gleichzeitig Ausreißerverhalten zu berücksichtigen. Mit Mean Shift Clustering können Kundenverhalten, Kaufmuster und demografische Daten analysiert werden, um natürliche Gruppierungen unabhängig von der Gruppengröße aufzudecken.
So lassen sich zielgerichtete Marketingstrategien und personalisierte Erlebnisse schaffen, die letztlich die Kundenbindung und -loyalität erhöhen.
Wie funktioniert das Mean Shift Clustering?
Beginnen wir mit einer Funktion zur Schätzung der Dichte von Datenpunkten in einem Fenster und verstehen wir, wie dieser Algorithmus funktioniert.
Kernel-Dichte-Schätzung (KDE)
Sie verwendet eine Wahrscheinlichkeitsdichtefunktion einer Zufallsvariablen, um in jeder Iteration Bereiche mit höherer Datendichte zu identifizieren. Die Formel für KDE lautet:
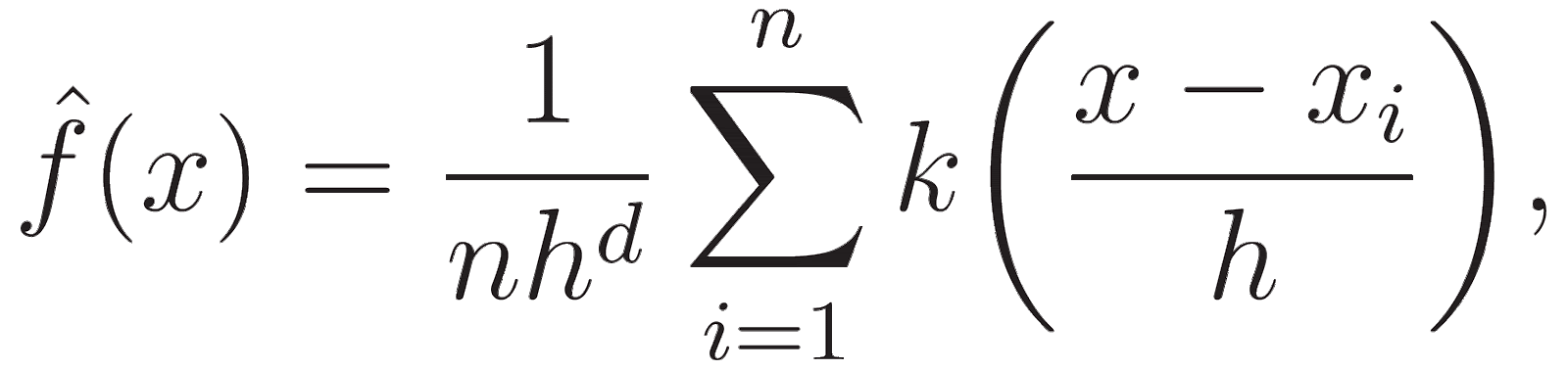
Dabei ist h ein Bandbreitenparameter und der Kernel ist in der Regel ein Gaußscher. Die Kernel-Funktion k glättet den Beitrag jedes Datenpunkts und sorgt dafür, dass Punkte, die näher an x liegen, einen höheren Einfluss auf die Dichteschätzung haben.
Die Wahl der richtigen Bandbreite
Der Bandbreitenparameter h bestimmt die Größe der Nachbarschaft um jeden Datenpunkt und hat damit einen direkten Einfluss auf die Clustering-Ergebnisse. Hier sind Methoden zur Auswahl der Bandbreite:
Scotts Regel
Die Scott'sche Regel ist ein heuristischer Ansatz, der eine Faustregel für die Bandbreitenauswahl liefert. Sie gleicht Verzerrung und Varianz in der Dichteschätzung aus, was sie zu einem guten Ausgangspunkt für viele Anwendungen macht.
wo:
- n ist die Anzahl der Datenpunkte.
- d ist die Anzahl der Dimensionen des Datensatzes.
Silbermans Regel
Ähnlich wie die Scott-Regel bietet die Silverman-Regel einen weiteren heuristischen Ansatz für die Bandbreitenauswahl, der besonders für unimodale Verteilungen nützlich ist.
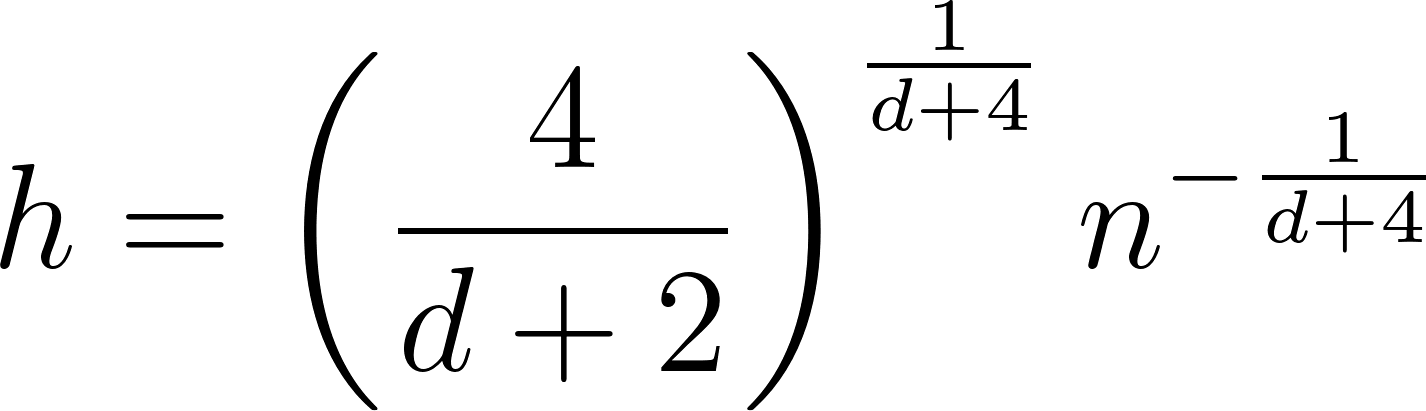
Kreuzvalidierung
Indem wir die Leistung verschiedener Bandbreitenwerte an den Holdout-Datensätzen bewerten, können wir den besten Bandbreitenwert wählen, der den Fehler minimiert und die besten Clustering-Ergebnisse liefert.
- Teilen Sie Teile die Daten in Trainings- und Validierungssätze auf.
- Wende an. Mean Shift Clustering mit verschiedenen Bandbreitenwerten auf die Trainingsmenge.
- Bewerte die Leistung der einzelnen Bandbreiten in der Validierungsmenge.
- Wähle die Bandbreite, die den Fehler minimiert.
Expertenwissen
Expertenwissen kann wertvolle Erkenntnisse über die Auswahl der geeigneten Bandbreite liefern, insbesondere bei speziellen Anwendungen wie der Bildverarbeitung. Ein Experte könnte die typische Skala der Merkmale im Bild verstehen, um den optimalen Bandbreitenbereich zu wählen und diesen Bereich dann durch empirische Tests fein abzustimmen.
Adaptive Bandbreite
Die adaptive Bandbreite ist nützlich für Datensätze mit unterschiedlichen Dichten. Sie wendet unterschiedliche Bandbreiten für verschiedene Regionen der Daten an. Es beginnt mit einer globalen Bandbreitenschätzung und passt sie dann lokal auf der Grundlage der Dichte der Datenpunkte in dieser Region an.
Mittlerer Verschiebungsvektor
Der mittlere Verschiebungsvektor stellt die Größe und Richtung der Bewegung dar, die erforderlich ist, um die Schätzung des Clustermittelpunkts von Gebieten mit geringerer Dichte in Regionen mit höherer Dichte zu verschieben.
Für einen Datenpunkt xider Vektor der Mittelwertverschiebung m(xi) wie folgt berechnet:
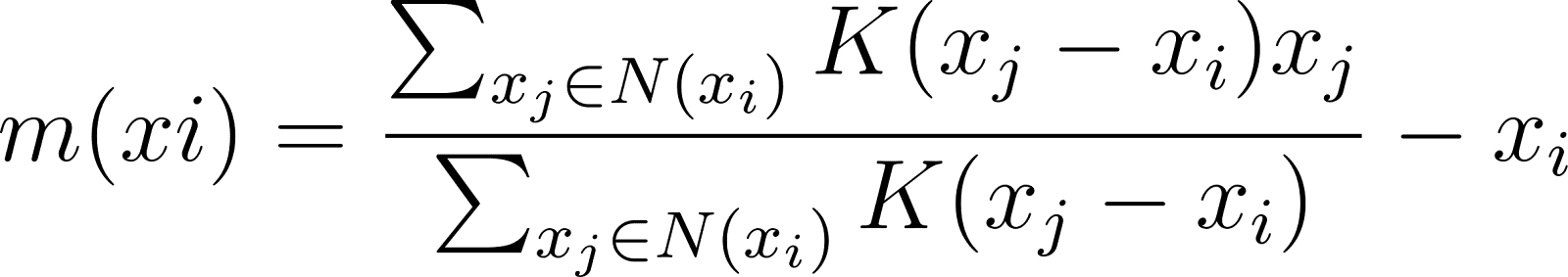
wobei N(xi) die Nachbarschaft um xi durch die Bandbreite definiert.
Konvergenz
Der Mean-Shift-Clustering-Algorithmus konvergiert, wenn sich die Clusterzentren nicht mehr über einen bestimmten Schwellenwert hinaus bewegen und wenn der Algorithmus die Modi der Dichtefunktion identifiziert hat, um die herum die Cluster gebildet werden. Der Algorithmus durchläuft die folgenden Schritte, bis er konvergiert:
- Berechne den mittleren Verschiebungsvektor für jeden Datenpunkt.
- Verschiebung den Datenpunkt in Richtung des Mittelwerts seiner Nachbarschaft.
- Prüfe auf Konvergenz, indem du feststellst, ob die Verschiebungen kleiner als ein vordefinierter Schwellenwert sind.
Konvergenz bedeutet, dass sich die Datenpunkte um die lokalen Maxima der Dichtefunktion stabilisiert haben, die dann als Clusterzentren dienen.
Werde ein ML-Wissenschaftler
Implementierung des Mean Shift Clustering in Python
Jetzt ist es an der Zeit, die Schritte für das Mean Shift Clustering zu erkunden. Wir werden die Klasse MeanShift aus der beliebten Bibliothek sci-kit-learn verwenden, die sofort verfügbar ist, um diesen Algorithmus auf Datensätze anzuwenden.
Basic Mean Shift Clustering
Beginnen wir damit, die erforderlichen Bibliotheken für die Implementierung zu importieren.
from sklearn.cluster import MeanShift, estimate_bandwidth
from sklearn.datasets import make_blobs
import matplotlib.pyplot as pltAls Nächstes erzeugen wir einen synthetischen Datensatz mit 500 Stichproben, indem wir die Funktion make_blobs() aus dem Modul datasets von scikit-learnverwenden. Der Datensatz hat fünf Zentren, d. h. Cluster, mit einer Standardabweichung von 0,7 Clustern.
# Create a sample dataset
X, _ = make_blobs(n_samples=500, centers=5, cluster_std=0.7, random_state=27)Schätzen wir die Bandbreite mithilfe der Funktion estimate_bandwidth().
# Estimate the bandwidth of the input data
bandwidth = estimate_bandwidth(X, quantile=0.2, n_samples=500)Jetzt verwenden wir diese Bandbreitennummer, um das MeanShift Clustering-Objekt zu initialisieren und es auf den zuvor erstellten Datensatz anzupassen.
# Perform mean shift clustering
ms_model = MeanShift(bandwidth=bandwidth, bin_seeding=True)
ms_model.fit(X)
labels = ms_model.labels_
mean_shift_centers = ms_model.cluster_centers_Es ist an der Zeit, die Mittelwertverschiebung der Clusterzentren in unserem Originaldatensatz zu visualisieren. Hier sind unsere fünf Cluster in verschiedenen Farben dargestellt, wobei die Zentren der Mittelwertverschiebung durch Kreuze gekennzeichnet sind.
# Plot the results
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='plasma', marker='p')
plt.scatter(mean_shift_centers[:, 0], mean_shift_centers[:, 1], s=250, c='blue', marker='X')
plt.title('mean shift clustering')
plt.xlabel('Attribute 1')
plt.ylabel('Attribute 2')
plt.show()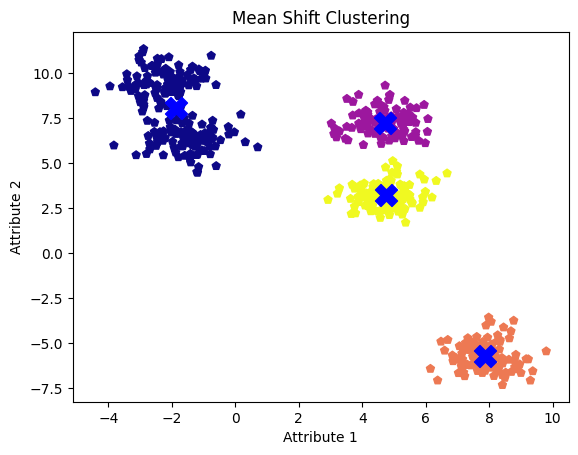
Mittelwertverschiebung von Clustern mit Standard-Bandbreitenwert. Bild vom Autor
Obwohl wir fünf Blobs oder Cluster beobachten, identifiziert der Algorithmus nur vier, indem er zwei benachbarte Cluster zu einem zusammenfasst.
Parameter Abstimmbandbreite
Der Parameter bandwidth hat einen großen Einfluss auf die Clustering-Ergebnisse. Lass uns testen, ob wir die fünf Cluster finden können. Wir testen drei verschiedene Bandbreitenwerte und visualisieren die resultierenden Clusterzentren für jeden.
# Try different bandwidth values
bandwidth_values = [0.1, 1.0, 2.0]
for bw in bandwidth_values:
ms = MeanShift(bandwidth=bw, bin_seeding=True)
ms.fit(X)
labels = ms.labels_
cluster_centers = ms.cluster_centers_
print("Bandwidth Value:", bw)
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='plasma', marker='p')
plt.scatter(cluster_centers[:, 0], cluster_centers[:, 1], s=250, c='blue', marker='X')
plt.title('mean shift clustering')
plt.xlabel('Attribute 1')
plt.ylabel('Attribute 2')
plt.show()
Mittelwertverschiebung von Clustern mit einem Bandbreitenwert von 0,1. Bild vom Autor
Mittlere Verschiebung von Clustern mit einem Bandbreitenwert von 1,0. Bild vom Autor
Mittlere Verschiebung von Clustern mit einem Bandbreitenwert von 2,0. Bild vom Autor
Der Bandbreitenwert von 0,1 scheint zu niedrig zu sein, wodurch der Algorithmus jeden Datenpunkt als eigenen Cluster behandelt. Andererseits erscheint ein Bandbreitenwert von 2,0 etwas hoch, da er die beiden Cluster in unserem ersten Versuch nicht trennte. Ein Bandbreitenwert von 1,0 erweist sich als optimal, da er alle fünf Cluster und ihre Zentren deutlich erkennen lässt.
Wählen wir diesen Wert aus und visualisieren wir die Ergebnisse noch einmal.
ms = MeanShift(bandwidth=1.0, bin_seeding=True)
ms.fit(X)
labels = ms.labels_
cluster_centers = ms.cluster_centers_
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='plasma', marker='p')
plt.scatter(cluster_centers[:, 0], cluster_centers[:, 1], s=250, c='blue', marker='X')
plt.title('mean shift clustering')
plt.xlabel('Attribute 1')
plt.ylabel('Attribute 2')
plt.show()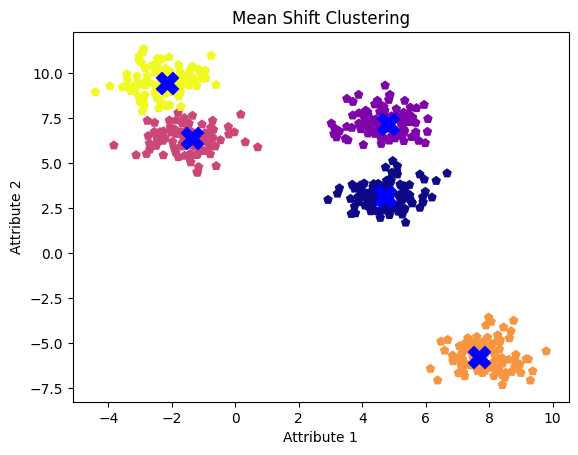
Mittlere Verschiebung von Clustern mit einem Bandbreitenwert von 1,0
Wie beobachtet, führt eine kleinere Bandbreite tendenziell zu mehr Clustern, während eine größere Bandbreite zur Verschmelzung von Clustern führen kann.
Vergleich der Mittelwertverschiebung mit k-means
Vergleichen wir die Ergebnisse der Mittelwertverschiebung und des k-means Clustering mit demselben Datensatz. Importiere zunächst KMeans aus dem Modul cluster von sklearn. Als Nächstes setzen wir die Anzahl der Cluster auf drei und passen das Modell an, um die Clusterschwerpunkte zu erhalten.
from sklearn.cluster import KMeans
# Perform k-means Clustering
kmeans = KMeans(n_clusters=3, random_state=0, n_init='auto')
kmeans.fit(X)
kmeans_labels = kmeans.labels_
kmeans_centers = kmeans.cluster_centers_Jetzt wollen wir die Ergebnisse visualisieren, um sie mit den Ergebnissen des Mean Shift Clustering zu vergleichen.
plt.scatter(X[:, 0], X[:, 1], c=kmeans_labels, cmap='plasma', marker='p')
plt.scatter(kmeans_centers[:, 0], kmeans_centers[:, 1], s=250, c='red', marker='X')
plt.title('K-means Clustering')
plt.xlabel('Attribute 1')
plt.ylabel('Attribute 2')
plt.show()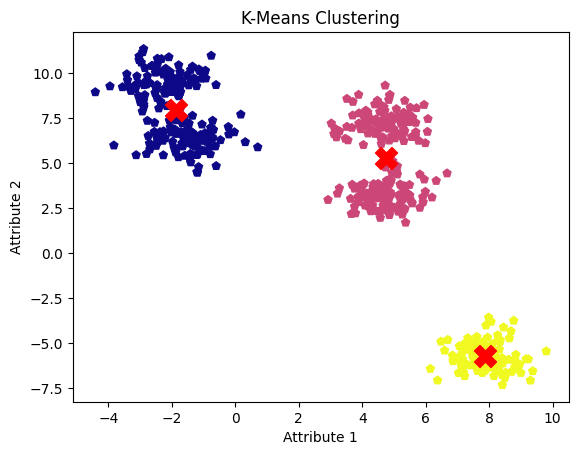
k-means Clustering Ergebnisse. Bild vom Autor
Der Nachteil des k-means Clustering-Algorithmus ist, dass die Anzahl der Cluster im Voraus festgelegt werden muss, was dazu führen kann, dass benachbarte Cluster zu einem verschmolzen werden. Mit einem gut abgestimmten Mean-Shift-Clustermodell konnten jedoch alle fünf Cluster und ihre Zentren identifiziert werden.
Anwendungsfälle aus der realen Welt
Neben der Objekterkennung in der Bildverarbeitung wird das Mean Shift Clustering in einer Reihe von realen Anwendungen in verschiedenen Bereichen eingesetzt:
- Es unterstützt die Genexpressionsanalyse und die Vorhersage von Proteinstrukturen in der Bioinformatik.
- Geodatenanalysten nutzen sie für die geografische Clusterbildung und die Erkennung von Anomalien in räumlichen Daten.
- In der medizinischen Bildgebung wird sie zur Erkennung von Tumoren in MRT- und CT-Scans sowie zur Gewebeklassifizierung eingesetzt.
- Der Finanzsektor nutzt sie zur Marktsegmentierung und Betrugserkennung.
- In der natürlichen Sprachverarbeitung (NLP) wird sie außerdem zum Clustern von Dokumenten und zur Stimmungsanalyse eingesetzt.
Fazit
In diesem Beitrag haben wir gelernt, wie sich das Mean Shift Clustering an unterschiedliche Clusterformen und -größen anpasst, ohne dass eine bestimmte Anzahl von Clustern erforderlich ist.
Mit all den Einblicken und der praktischen Umsetzung dieses Algorithmus bist du bestens gerüstet, um ihn in deinen Projekten zu verwenden. Python ist die beliebteste Programmiersprache und es lohnt sich, sie zu lernen. Du kannst dich auf diese Python-Entwickler/innen-Karriere beziehen, um deine Python-Programmierkenntnisse auf die nächste Stufe zu bringen. Sieh dir auch unseren Karriereplan für Machine Learning Scientist mit Python an und lerne von Experten.
Werde ein ML-Wissenschaftler
Bilde dich in Python weiter, um ein/e Wissenschaftler/in für maschinelles Lernen zu werden.
