O clustering é uma técnica de aprendizado de máquina não supervisionada que identifica estruturas ocultas nos dados para ajudar as empresas a tomar decisões mais informadas. Alguns dos aplicativos de agrupamento mais comuns são a segmentação de imagens, a segmentação de clientes e a análise de redes sociais.
Com base no fato de o algoritmo exigir uma entrada de um número predeterminado de clusters ou a distribuição de dados, o clustering é de dois tipos: paramétrico e não paramétrico. Nesta publicação, abordaremos detalhadamente um desses algoritmos não paramétricos: o algoritmo de agrupamento de deslocamento médio. Discutiremos seus princípios subjacentes, exploraremos suas aplicações em diferentes setores e forneceremos uma implementação em Python. No final, vamos compará-la com a popular técnica de agrupamento k-means.
O que é clustering de deslocamento médio?
O clustering de deslocamento médio é usado para identificar clusters em conjuntos de dados em que o número de clusters não é conhecido de antemão. Ele encontra clusters deslocando iterativamente os pontos de dados para as regiões mais densas no espaço de recursos. Isso o torna particularmente útil para aplicações como reconhecimento de objetos, em que ele pode segmentar imagens com base na intensidade e na cor do pixel, e também para rastrear objetos em sequências de vídeo.
Como um algoritmo de busca de modo, ele rotula os clusters encontrando os modos, ou picos, na distribuição de dados. Essencialmente, ele destaca as áreas mais densas. Isso é feito deslocando iterativamente os centros de cluster para regiões de maior densidade de dados. Aqui estão as etapas:
- Inicialização: Comece considerando cada ponto de dados como um candidato em potencial para o centro do cluster.
- Densidade Estimativa: Para cada ponto de dados, defina uma janela ao redor dele, chamada de raio, e calcule a média dos pontos de dados dentro desse raio.
- Mudança: Desloque cada ponto para essa posição média. Essa etapa move o ponto em direção à região de maior densidade.
- Convergência: Repita as etapas 2 e 3 iterativamente até a convergência, ou seja, quando o deslocamento for menor que um limite predefinido. A mudança insignificante no deslocamento implica que os pontos se estabilizaram em torno dos máximos locais da função de densidade.
No final desse processo iterativo, os pontos de dados se agrupam em torno dos modos da distribuição de dados, formando os clusters. A mudança de média é particularmente flexível porque se baseia na distribuição real dos dados em vez de assumir uma forma predefinida para os clusters, o que permite lidar com clusters de formas arbitrárias.
Por que usar o clustering de deslocamento médio?
O clustering de deslocamento médio é uma ferramenta poderosa para descobrir a estrutura subjacente dos dados sem fazer nenhuma suposição sobre seus parâmetros, como o número de clusters ou sua forma. Considerando sua abordagem baseada em densidade que se concentra em regiões de alta densidade de dados, ela é robusta contra outliers, garantindo assim que os dados ruidosos tenham um impacto mínimo no processo de agrupamento. Essa robustez o torna adequado para conjuntos de dados do mundo real, que geralmente contêm irregularidades e ruídos, e também para aplicativos que exigem adaptabilidade e precisão.
Alguns dos cenários do mundo real em que o clustering de deslocamento médio funciona bem são:
Segmentação de imagens
O algoritmo de agrupamento de deslocamento médio pode segmentar imagens em regiões com base na intensidade ou na cor do pixel sem exigir conhecimento prévio do número de segmentos. Essa flexibilidade o torna altamente eficaz para tarefas de segmentação de imagens, pois os clusters gerados com o mean shift clustering podem ter qualquer forma ou tamanho.
Segmentação de imagens usando agrupamento de deslocamento médio. Fonte: ResearchGate
Além disso, as imagens que contêm ruído, especialmente em condições de pouca luz, são difíceis de segmentar. Para esses cenários, o algoritmo de agrupamento de deslocamento médio fornece uma segmentação mais natural e precisa, o que é essencial em aplicações como imagens médicas para detectar tipos de tecidos anormais ou em visão computacional para detecção confiável de objetos.
Rastreamento de objetos em análise de vídeo
Após suas vantagens na segmentação de imagens, o agrupamento de deslocamento médio é usado com frequência no rastreamento de objetos em fluxos de vídeo. Sua capacidade de identificar e seguir objetos dinamicamente à medida que eles se movem pelos quadros torna-o bastante eficaz para aplicativos de rastreamento em tempo real.

Agrupamento de deslocamento médio no rastreamento de objetos. Fonte: ResearchGate
Ao se concentrar na densidade de pixels ou recursos associados ao objeto, o deslocamento médio pode rastrear com eficiência objetos de formas e tamanhos variados, adaptando-se facilmente às mudanças de movimento e aparência.
Segmentação de clientes em marketing
Para as empresas, é importante entender os segmentos de clientes sem pressupor um número fixo de categorias e, ao mesmo tempo, levar em conta o comportamento atípico. O clustering de deslocamento médio pode analisar o comportamento do cliente, os padrões de compra e os dados demográficos para descobrir agrupamentos naturais, independentemente do tamanho do grupo.
Isso ajuda a criar estratégias de marketing direcionadas e experiências personalizadas, melhorando, em última análise, o envolvimento e a retenção do cliente.
Como funciona o clustering de deslocamento médio?
Vamos começar com uma função para estimar a densidade dos pontos de dados em uma janela e entender como esse algoritmo funciona.
Estimativa de densidade de kernel (KDE)
Ele usa uma função de densidade de probabilidade de uma variável aleatória para identificar áreas de maior densidade de dados em cada iteração. A fórmula para o KDE é:
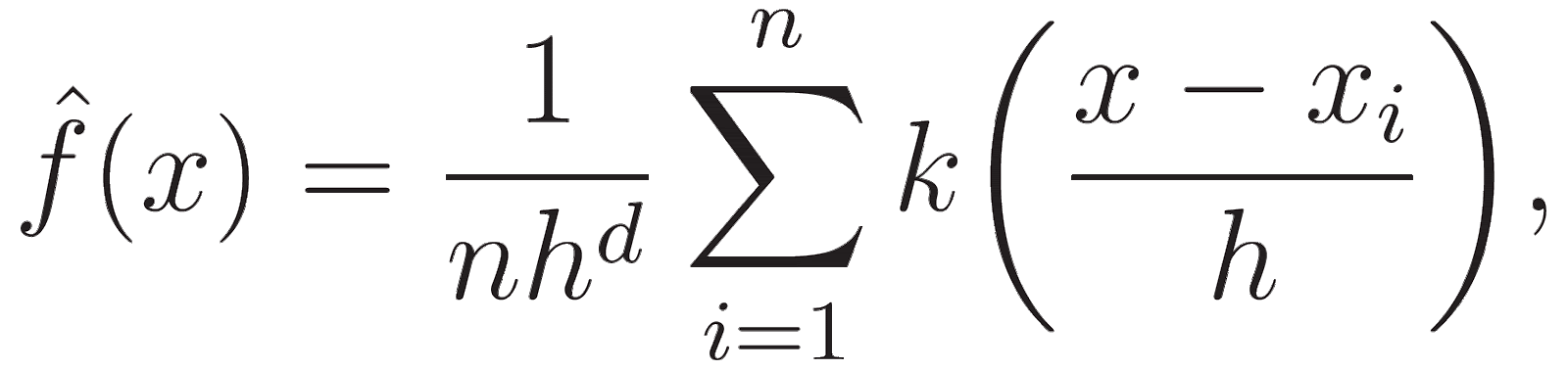
Onde h é um parâmetro de largura de banda, e o kernel é geralmente gaussiano. A função kernel k suaviza a contribuição de cada ponto de dados, garantindo que os pontos mais próximos de x tenham uma influência maior na estimativa da densidade.
Escolhendo a largura de banda correta
O parâmetro de largura de banda h determina o tamanho da vizinhança em torno de cada ponto de dados, influenciando diretamente os resultados do agrupamento. Aqui estão os métodos para você selecionar a largura de banda:
A regra de Scott
A regra de Scott é uma abordagem heurística que fornece uma regra geral para a seleção da largura de banda. Ele equilibra o viés e a variação na estimativa de densidade, tornando-o um bom ponto de partida para muitas aplicações.

onde:
- n é o número de pontos de dados.
- d é o número de dimensões no conjunto de dados.
Regra de Silverman
Semelhante à regra de Scott, a regra de Silverman oferece outra abordagem heurística para a seleção de largura de banda, particularmente útil para distribuições unimodais.
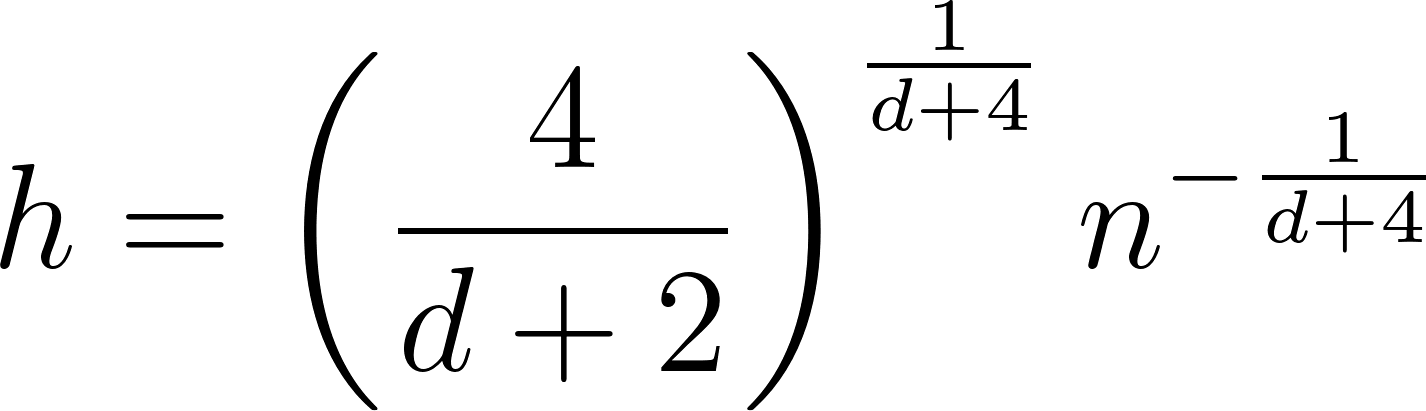
Validação cruzada
Ao avaliar o desempenho de diferentes valores de largura de banda nos conjuntos de dados de holdout, podemos escolher o melhor valor de largura de banda que minimiza o erro e produz os melhores resultados de clustering.
- Dividir Divida os dados em conjuntos de treinamento e validação.
- Aplicar clustering de deslocamento médio com diferentes valores de largura de banda no conjunto de treinamento.
- Avalie o desempenho correspondente a cada largura de banda no conjunto de validação.
- Selecione a largura de banda que minimiza o erro.
Conhecimento especializado
O conhecimento especializado pode fornecer informações valiosas sobre a seleção da largura de banda adequada, especialmente em aplicativos específicos, como o processamento de imagens. Um especialista pode entender a escala típica dos recursos na imagem para escolher o intervalo ideal de largura de banda e, em seguida, ajustar esse intervalo por meio de testes empíricos.
Largura de banda adaptável
A largura de banda adaptável é útil para conjuntos de dados com densidades variáveis. Ele aplica diferentes larguras de banda para diferentes regiões dos dados. Ele começa com uma estimativa de largura de banda global e, em seguida, ajusta-a localmente com base na densidade dos pontos de dados nessa região.
Vetor de deslocamento médio
O vetor de deslocamento médio representa a magnitude e a direção do movimento necessário para deslocar a estimativa do centro do cluster de áreas de densidade mais baixa para regiões de densidade mais alta.
Para um ponto de dados xio vetor de deslocamento médio m(xi) é calculado como:
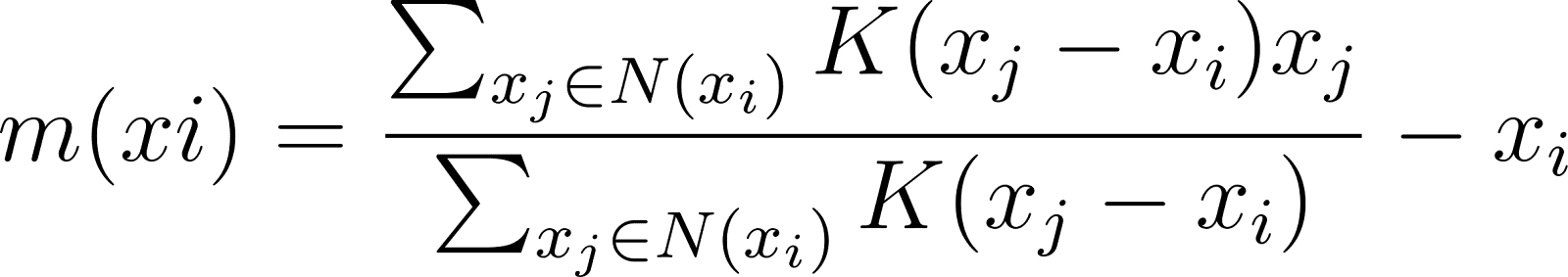
onde N(xi) denota a vizinhança em torno de xi definido pela largura de banda.
Convergência
O algoritmo de agrupamento de deslocamento médio converge quando os centros de agrupamento não se movem mais além de um limite especificado e quando o algoritmo identificou os modos da função de densidade, em torno dos quais os agrupamentos são formados. O algoritmo continua iterando pelas etapas a seguir até a convergência:
- Calcule o vetor de deslocamento médio para cada ponto de dados.
- Deslocar o ponto de dados em direção à média de sua vizinhança.
- Verifique Verifique a convergência determinando se os deslocamentos são menores que um limite predefinido.
A convergência indica que os pontos de dados se estabilizaram em torno dos máximos locais da função de densidade, que servem como centros de cluster.
Torne-se um cientista de ML
Implementação do clustering de deslocamento médio em Python
É hora de explorar as etapas envolvidas no uso do clustering de deslocamento médio. Usaremos a classe MeanShift da popular biblioteca sci-kit-learn, que está disponível imediatamente para você aplicar esse algoritmo a conjuntos de dados.
Clustering de deslocamento médio básico
Vamos começar importando as bibliotecas necessárias para a implementação.
from sklearn.cluster import MeanShift, estimate_bandwidth
from sklearn.datasets import make_blobs
import matplotlib.pyplot as pltEm seguida, geraremos um conjunto de dados sintético de 500 amostras usando a função make_blobs() do módulo datasets de scikit-learn. O conjunto de dados terá cinco centros, ou seja, clusters, com um desvio padrão de cluster de 0,7.
# Create a sample dataset
X, _ = make_blobs(n_samples=500, centers=5, cluster_std=0.7, random_state=27)Vamos estimar a largura de banda usando a função estimate_bandwidth().
# Estimate the bandwidth of the input data
bandwidth = estimate_bandwidth(X, quantile=0.2, n_samples=500)Agora, usaremos esse número de largura de banda para inicializar o objeto de agrupamento MeanShift e ajustá-lo ao conjunto de dados que criamos anteriormente.
# Perform mean shift clustering
ms_model = MeanShift(bandwidth=bandwidth, bin_seeding=True)
ms_model.fit(X)
labels = ms_model.labels_
mean_shift_centers = ms_model.cluster_centers_É hora de visualizar os centros de cluster de deslocamento médio em nosso conjunto de dados original. Aqui, nossos cinco clusters são representados em cores diferentes com centros de deslocamento médio representados por cruzes.
# Plot the results
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='plasma', marker='p')
plt.scatter(mean_shift_centers[:, 0], mean_shift_centers[:, 1], s=250, c='blue', marker='X')
plt.title('mean shift clustering')
plt.xlabel('Attribute 1')
plt.ylabel('Attribute 2')
plt.show()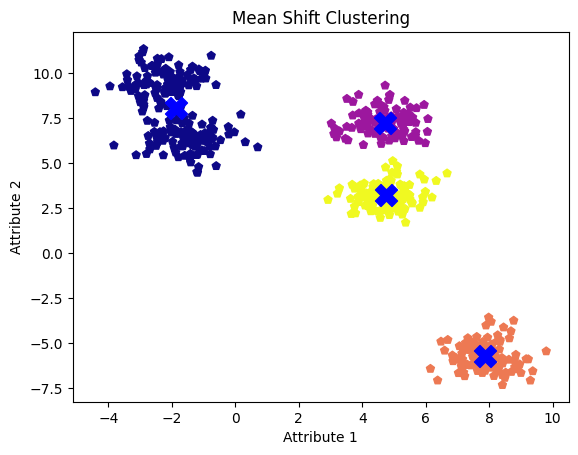
Clusters de deslocamento médio com valor de largura de banda padrão. Imagem do autor
Embora observemos cinco bolhas ou clusters, o algoritmo identifica apenas quatro, mesclando dois clusters adjacentes em um.
Parâmetro de largura de banda de ajuste
O parâmetro bandwidth tem um impacto significativo nos resultados de agrupamento. Vamos ajustá-lo para ver se conseguimos encontrar os cinco clusters. Testaremos três valores diferentes de largura de banda e visualizaremos os centros de cluster resultantes para cada um deles.
# Try different bandwidth values
bandwidth_values = [0.1, 1.0, 2.0]
for bw in bandwidth_values:
ms = MeanShift(bandwidth=bw, bin_seeding=True)
ms.fit(X)
labels = ms.labels_
cluster_centers = ms.cluster_centers_
print("Bandwidth Value:", bw)
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='plasma', marker='p')
plt.scatter(cluster_centers[:, 0], cluster_centers[:, 1], s=250, c='blue', marker='X')
plt.title('mean shift clustering')
plt.xlabel('Attribute 1')
plt.ylabel('Attribute 2')
plt.show()
Clusters de deslocamento médio com valor de largura de banda de 0,1. Imagem do autor
Clusters de deslocamento médio com valor de largura de banda de 1,0. Imagem do autor
Clusters de deslocamento médio com valor de largura de banda de 2,0. Imagem do autor
O valor da largura de banda de 0,1 parece ser muito baixo, fazendo com que o algoritmo trate cada ponto de dados como um cluster separado. Por outro lado, um valor de largura de banda de 2,0 parece um pouco alto, pois não separou os dois clusters em nossa primeira tentativa. Um valor de largura de banda de 1,0 prova ser o mais ideal, revelando claramente todos os cinco clusters e seus centros.
Vamos selecionar esse valor e visualizar os resultados mais uma vez.
ms = MeanShift(bandwidth=1.0, bin_seeding=True)
ms.fit(X)
labels = ms.labels_
cluster_centers = ms.cluster_centers_
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='plasma', marker='p')
plt.scatter(cluster_centers[:, 0], cluster_centers[:, 1], s=250, c='blue', marker='X')
plt.title('mean shift clustering')
plt.xlabel('Attribute 1')
plt.ylabel('Attribute 2')
plt.show()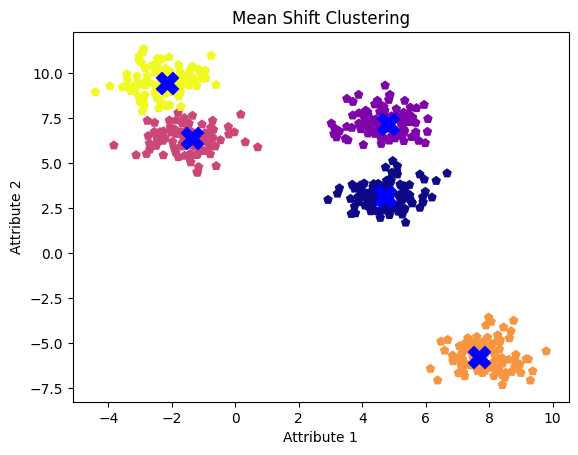
Clusters de deslocamento médio com valor de largura de banda de 1,0
Conforme observado, uma largura de banda menor tende a produzir mais clusters, enquanto uma largura de banda maior pode levar à fusão de clusters.
Comparação do deslocamento médio com o k-means
Vamos comparar os resultados do mean shift e do k-means clustering no mesmo conjunto de dados. Primeiro, importe KMeans do módulo cluster de sklearn. Em seguida, definiremos o número de clusters como três e ajustaremos o modelo para obter os centroides dos clusters.
from sklearn.cluster import KMeans
# Perform k-means Clustering
kmeans = KMeans(n_clusters=3, random_state=0, n_init='auto')
kmeans.fit(X)
kmeans_labels = kmeans.labels_
kmeans_centers = kmeans.cluster_centers_Agora, vamos visualizar os resultados para compará-los com os resultados do clustering de deslocamento médio.
plt.scatter(X[:, 0], X[:, 1], c=kmeans_labels, cmap='plasma', marker='p')
plt.scatter(kmeans_centers[:, 0], kmeans_centers[:, 1], s=250, c='red', marker='X')
plt.title('K-means Clustering')
plt.xlabel('Attribute 1')
plt.ylabel('Attribute 2')
plt.show()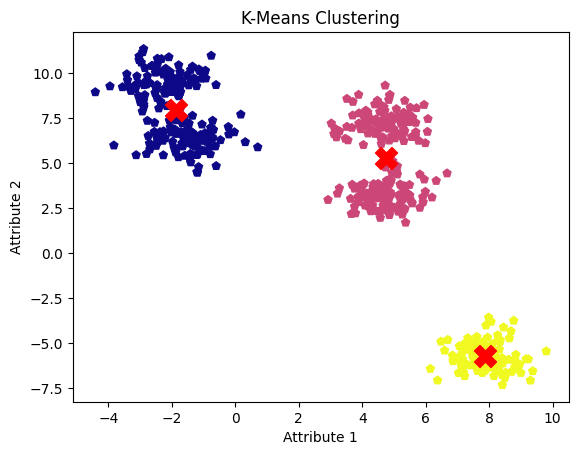
Resultados do agrupamento k-means. Imagem do autor
A desvantagem do algoritmo de agrupamento k-means é que ele exige a especificação prévia do número de clusters, o que pode levar à fusão de clusters adjacentes em um só. No entanto, um modelo de agrupamento de deslocamento médio bem ajustado identificou com sucesso todos os cinco agrupamentos e seus centros.
Casos de uso no mundo real
Além do reconhecimento de objetos no processamento de imagens, o agrupamento de deslocamento médio é usado em várias aplicações do mundo real em vários domínios:
- Ele oferece suporte à análise de expressão gênica e à previsão de estrutura de proteínas em bioinformática.
- Os analistas geoespaciais o utilizam para agrupamento geográfico e detecção de anomalias em dados espaciais.
- Em imagens médicas, ele é usado para detectar tumores em exames de ressonância magnética e tomografia computadorizada, bem como para classificação de tecidos.
- O setor financeiro o utiliza para segmentação de mercado e detecção de fraudes.
- Além disso, no processamento de linguagem natural (NLP), ele é aplicado ao agrupamento de documentos e à análise de sentimentos.
Conclusão
Nesta postagem, aprendemos como o clustering de deslocamento médio se adapta a formas e tamanhos variados de clusters, tudo isso sem precisar de um número predefinido de clusters.
Com todos os insights e a implementação prática desse algoritmo, você está pronto para fazer experiências com ele em seus projetos. Python é a linguagem de programação mais popular e vale a pena aprender. Você pode consultar esta trilha de carreira de Desenvolvedor Python para levar suas habilidades de programação Python para o próximo nível. Além disso, confira nossa trilha de carreira completa de Cientista de Aprendizado de Máquina com Python e aprenda com especialistas.
Torne-se um cientista de ML

Transformador de dados e estrategista de IA | Palestrante internacional | Ético em IA | Inventor | Mulher de sucesso global | Autor
Perguntas frequentes
O que é clustering de deslocamento médio?
O clustering de deslocamento médio é um algoritmo não paramétrico usado para identificar clusters nos dados, deslocando iterativamente os pontos para regiões de maior densidade de dados. Ele é flexível e não exige um número predefinido de clusters.
Como o clustering de deslocamento médio difere do k-means?
Diferentemente do k-means, que exige a especificação prévia do número de clusters, o mean shift clustering identifica o número de clusters automaticamente com base na densidade dos dados, o que o torna mais adaptável a formas variadas de clusters.
Quais são as aplicações reais do clustering de deslocamento médio?
O agrupamento de deslocamento médio é usado na segmentação de imagens, no rastreamento de objetos em análise de vídeo, na segmentação de clientes em marketing e em campos como bioinformática, imagens médicas e finanças para tarefas como detecção de anomalias e detecção de fraudes.
Como você seleciona o parâmetro de largura de banda no clustering de deslocamento médio?
O parâmetro de largura de banda, que influencia os resultados do agrupamento, pode ser selecionado usando métodos como a regra de Scott, a regra de Silverman, a validação cruzada ou o conhecimento especializado. A largura de banda adaptável também pode ser usada para conjuntos de dados com densidades variáveis.
Quais são as principais etapas da implementação do clustering de deslocamento médio em Python?
Para implementar o clustering de deslocamento médio em Python, você estima a largura de banda, inicializa o objeto MeanShift, ajusta-o aos dados e visualiza os resultados. Você também pode ajustar o parâmetro de largura de banda para obter os melhores resultados de agrupamento.


