Agrupación por Desplazamiento Medio: Guía completa
La agrupación es una técnica de aprendizaje automático no supervisado que identifica estructuras ocultas en los datos para ayudar a las empresas a tomar decisiones más informadas. Algunas de las aplicaciones más comunes de la agrupación son la segmentación de imágenes, la segmentación de clientes y el análisis de redes sociales.
Según si el algoritmo requiere una entrada de un número predeterminado de conglomerados o la distribución de los datos, la agrupación es de dos tipos: paramétrica y no paramétrica. En este post, trataremos en detalle uno de estos algoritmos no paramétricos: el algoritmo de agrupación por desplazamiento medio. Discutiremos sus principios subyacentes, exploraremos sus aplicaciones en diferentes industrias y proporcionaremos una implementación en Python. Al final, la compararemos con la popular técnica de agrupación k-means.
¿Qué es la Agrupación de Desplazamiento Medio?
La agrupación por desplazamiento de la media se utiliza para identificar conglomerados en conjuntos de datos en los que no se conoce de antemano el número de conglomerados. Encuentra conglomerados desplazando iterativamente los puntos de datos hacia las regiones más densas del espacio de características. Esto lo hace especialmente útil para aplicaciones como el reconocimiento de objetos, donde puede segmentar imágenes basándose en la intensidad y el color de los píxeles, y también para el seguimiento de objetos en secuencias de vídeo.
Como algoritmo de búsqueda de modos, etiqueta los conglomerados encontrando los modos, o picos, en la distribución de los datos. Esencialmente, destaca las zonas más densas. Para ello, desplaza iterativamente los centros de los conglomerados hacia regiones de mayor densidad de datos. Estos son los pasos:
- Inicialización: Empieza por considerar cada punto de datos como un candidato potencial para el centro del conglomerado.
- Densidad Estimación: Para cada punto de datos, define una ventana a su alrededor, llamada radio, y luego calcula la media de los puntos de datos dentro de este radio.
- Cambiando: Desplaza cada punto a esta posición media. Este paso desplaza el punto hacia la región de mayor densidad.
- Convergencia: Repite los pasos 2 y 3 iterativamente hasta la convergencia, es decir, cuando el desplazamiento sea menor que un umbral predefinido. El cambio insignificante en el desplazamiento implica que los puntos se han estabilizado en torno a los máximos locales de la función de densidad.
Al final de este proceso iterativo, los puntos de datos se agrupan en torno a las modas de la distribución de datos, formando los conglomerados. El desplazamiento de la media es especialmente flexible porque se basa en la distribución real de los datos en lugar de asumir una forma predefinida para los conglomerados, lo que le permite manejar conglomerados de formas arbitrarias.
¿Por qué utilizar la agrupación por desplazamiento medio?
La agrupación por desplazamiento de medias es una potente herramienta para descubrir la estructura subyacente de los datos sin hacer ninguna suposición sobre sus parámetros, como el número de conglomerados o su forma. Teniendo en cuenta su enfoque basado en la densidad, que se centra en las regiones de alta densidad de datos, es robusto frente a los valores atípicos, garantizando así que los datos ruidosos tengan un impacto mínimo en el proceso de agrupación. Esta robustez lo hace adecuado para los conjuntos de datos del mundo real, que a menudo contienen irregularidades y ruido, y también para las aplicaciones que requieren adaptabilidad y precisión.
Algunos de los escenarios del mundo real en los que la agrupación por desplazamiento medio funciona bien son:
Segmentación de imágenes
El algoritmo de agrupación por desplazamiento medio puede segmentar las imágenes en regiones basándose en la intensidad o el color de los píxeles, sin necesidad de conocer previamente el número de segmentos. Esta flexibilidad lo hace muy eficaz para las tareas de segmentación de imágenes, porque los conglomerados generados mediante la agrupación por desplazamiento medio pueden tener cualquier forma o tamaño.
Segmentación de imágenes mediante agrupación por desplazamiento medio. Fuente: ResearchGate
Además, las imágenes que contienen ruido, sobre todo en condiciones de poca luz, son difíciles de segmentar. En estos casos, el algoritmo de agrupación por desplazamiento medio proporciona una segmentación más natural y precisa, que es esencial en aplicaciones como las imágenes médicas para detectar tipos de tejido anormales o en visión por ordenador para la detección fiable de objetos.
Seguimiento de objetos en el análisis de vídeo
Tras sus ventajas en la segmentación de imágenes, la agrupación por desplazamiento medio se utiliza con frecuencia en el seguimiento de objetos dentro de secuencias de vídeo. Su capacidad para identificar y seguir dinámicamente los objetos a medida que se mueven por los fotogramas lo hace muy eficaz para aplicaciones de seguimiento en tiempo real.
Agrupación de desplazamiento medio en el seguimiento de objetos. Fuente: ResearchGate
Al centrarse en la densidad de píxeles o rasgos asociados al objeto, el desplazamiento medio puede rastrear eficazmente objetos de formas y tamaños variables, por lo que se adapta fácilmente a los cambios de movimiento y aspecto.
Segmentación de clientes en marketing
Para las empresas, es importante comprender los segmentos de clientes sin asumir un número fijo de categorías y, al mismo tiempo, tener en cuenta los comportamientos atípicos. La agrupación por desplazamiento medio puede analizar el comportamiento de los clientes, los patrones de compra y los datos demográficos para descubrir agrupaciones naturales, independientemente del tamaño del grupo.
Esto ayuda a crear estrategias de marketing específicas y experiencias personalizadas, mejorando en última instancia el compromiso y la retención de los clientes.
¿Cómo funciona la agrupación por desplazamiento medio?
Empecemos con una función para estimar la densidad de puntos de datos en una ventana y comprender cómo funciona este algoritmo.
Estimación de la densidad del núcleo (KDE)
Utiliza una función de densidad de probabilidad de una variable aleatoria para identificar las zonas de mayor densidad de datos en cada iteración. La fórmula de la KDE es
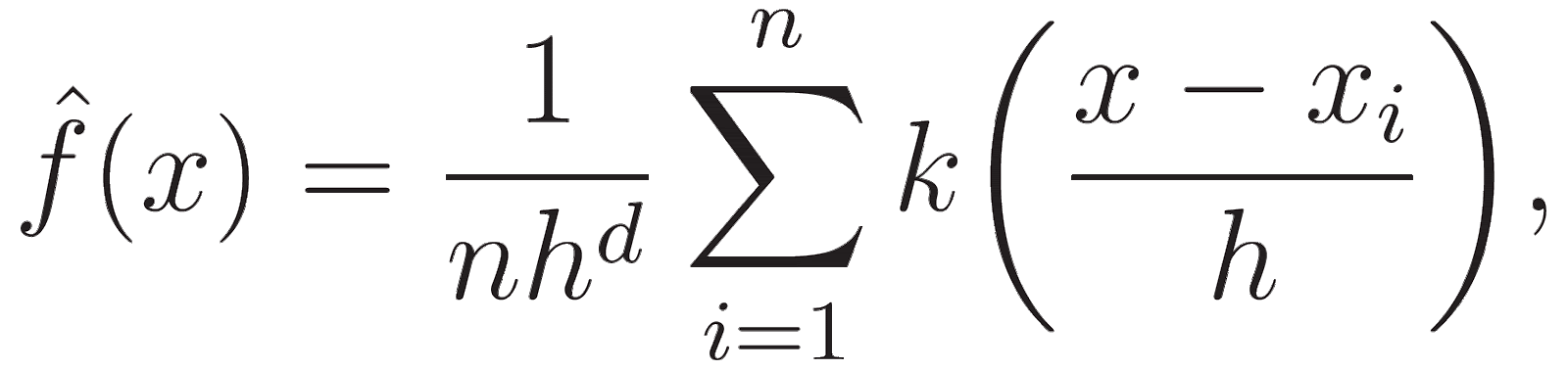
Donde h es un parámetro de ancho de banda, y el núcleo suele ser una gaussiana. La función k suaviza la contribución de cada punto de datos, asegurando que los puntos más cercanos a x tengan una mayor influencia en la estimación de la densidad.
Elegir el ancho de banda adecuado
El parámetro de ancho de banda h determina el tamaño del vecindario alrededor de cada punto de datos, influyendo directamente en los resultados de la agrupación. Aquí tienes métodos para seleccionar el ancho de banda:
La regla de Scott
La regla de Scott es un enfoque heurístico que proporciona una regla general para la selección del ancho de banda. Equilibra el sesgo y la varianza en la estimación de la densidad, por lo que es un buen punto de partida para muchas aplicaciones.
donde:
- n es el número de puntos de datos.
- d es el número de dimensiones del conjunto de datos.
La regla de Silverman
Similar a la regla de Scott, la regla de Silverman ofrece otro enfoque heurístico para la selección del ancho de banda especialmente útil para las distribuciones unimodales.
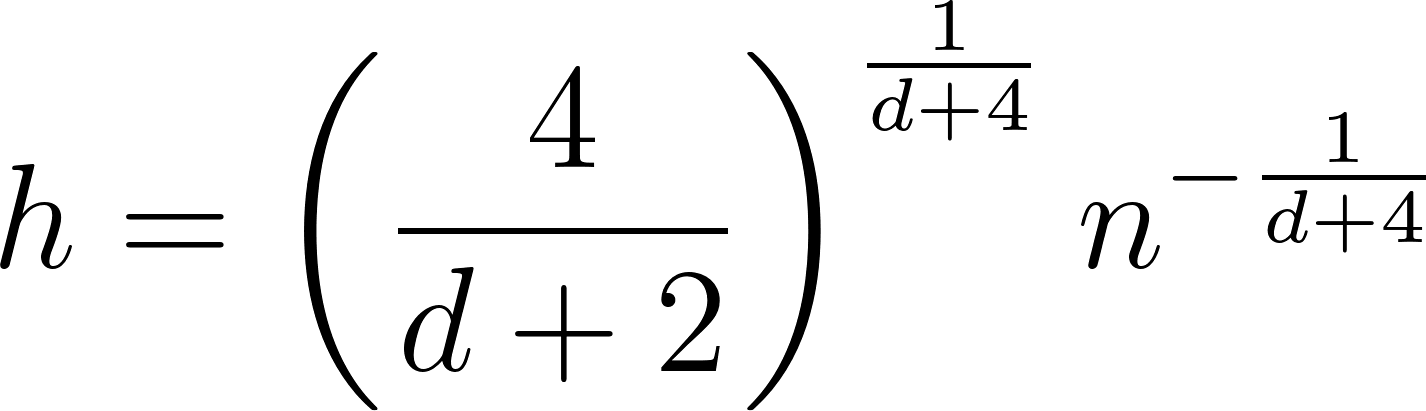
Validación cruzada
Evaluando el rendimiento de distintos valores de ancho de banda en los conjuntos de datos retenidos, podemos elegir el mejor valor de ancho de banda que minimice el error y produzca los mejores resultados de agrupación.
- Divide los datos en conjuntos de entrenamiento y validación.
- Aplica la agrupación por desplazamiento medio con distintos valores de ancho de banda en el conjunto de entrenamiento.
- Evalúa el rendimiento correspondiente a cada ancho de banda en el conjunto de validación.
- Selecciona el ancho de banda que minimice el error.
Conocimiento experto
Los conocimientos de los expertos pueden aportar información valiosa sobre la selección del ancho de banda adecuado, especialmente en aplicaciones específicas, como el procesamiento de imágenes. Un experto podría comprender la escala típica de los rasgos dentro de la imagen para elegir el rango óptimo de ancho de banda y luego afinar este rango mediante pruebas empíricas.
Ancho de banda adaptable
El ancho de banda adaptativo es útil para conjuntos de datos con densidades variables. Aplica anchos de banda diferentes para las distintas regiones de los datos. Empieza con una estimación global del ancho de banda y luego la ajusta localmente en función de la densidad de puntos de datos de esa región.
Vector de desplazamiento medio
El vector de desplazamiento medio representa la magnitud y la dirección del movimiento necesario para desplazar la estimación del centro del conglomerado de las zonas de menor densidad a las regiones de mayor densidad.
Para un punto de datos xiel vector de desplazamiento de la media m(xi) se calcula como:
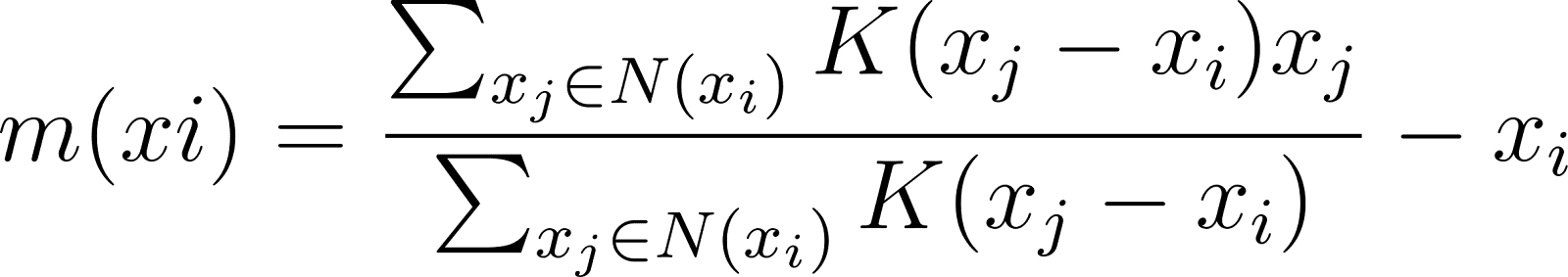
donde N(xi) denota la vecindad alrededor de xi definido por el ancho de banda.
Convergencia
El algoritmo de agrupación por desplazamiento medio converge cuando los centros de los conglomerados ya no se mueven más allá de un umbral especificado y cuando el algoritmo ha identificado los modos de la función de densidad, alrededor de los cuales se forman los conglomerados. El algoritmo sigue iterando a través de los pasos siguientes hasta la convergencia:
- Calcula el vector desplazamiento medio de cada punto de datos.
- Desplazamiento el punto de datos hacia la media de su vecindad.
- Comprueba la convergencia determinando si los desplazamientos son menores que un umbral predefinido.
La convergencia indica que los puntos de datos se han estabilizado en torno a los máximos locales de la función de densidad, que sirven entonces como centros de los conglomerados.
Conviértete en un Científico ML
Implementación de la agrupación por desplazamiento medio en Python
Es hora de explorar los pasos necesarios para utilizar la agrupación por desplazamiento medio. Utilizaremos la clase MeanShift de la popular biblioteca sci-kit-learn, que está disponible directamente para aplicar este algoritmo a conjuntos de datos.
Agrupación básica por desplazamiento de la media
Empecemos por importar las bibliotecas necesarias para la aplicación.
from sklearn.cluster import MeanShift, estimate_bandwidth
from sklearn.datasets import make_blobs
import matplotlib.pyplot as pltA continuación, generaremos un conjunto de datos sintéticos de 500 muestras utilizando la función make_blobs() del módulo datasets de scikit-learn. El conjunto de datos tendrá cinco centros, es decir, conglomerados, con una desviación típica de los conglomerados de 0,7.
# Create a sample dataset
X, _ = make_blobs(n_samples=500, centers=5, cluster_std=0.7, random_state=27)Vamos a estimar el ancho de banda utilizando la función estimate_bandwidth().
# Estimate the bandwidth of the input data
bandwidth = estimate_bandwidth(X, quantile=0.2, n_samples=500)Ahora, utilizaremos este número de ancho de banda para inicializar el objeto de agrupación MeanShift y ajustarlo sobre el conjunto de datos que hemos creado antes.
# Perform mean shift clustering
ms_model = MeanShift(bandwidth=bandwidth, bin_seeding=True)
ms_model.fit(X)
labels = ms_model.labels_
mean_shift_centers = ms_model.cluster_centers_Es hora de visualizar los centros de los conglomerados de desplazamiento medio sobre nuestro conjunto de datos original. Aquí, nuestros cinco conglomerados están representados en colores diferentes, con los centros de desplazamiento de la media representados por cruces.
# Plot the results
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='plasma', marker='p')
plt.scatter(mean_shift_centers[:, 0], mean_shift_centers[:, 1], s=250, c='blue', marker='X')
plt.title('mean shift clustering')
plt.xlabel('Attribute 1')
plt.ylabel('Attribute 2')
plt.show()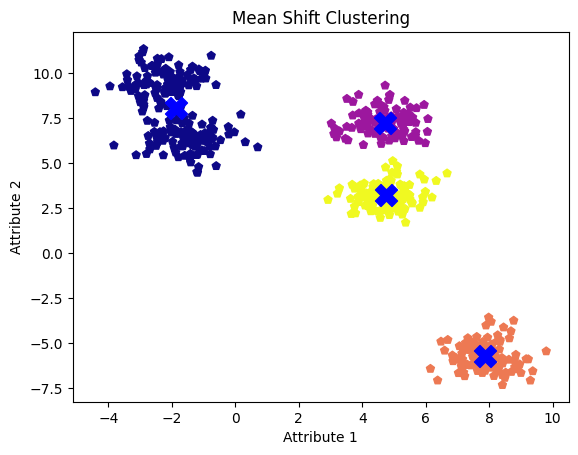
Conglomerados de desplazamiento medio con valor de ancho de banda por defecto. Imagen del autor
Aunque observamos cinco manchas o conglomerados, el algoritmo sólo identifica cuatro al fusionar dos conglomerados adyacentes en uno solo.
Parámetro de ajuste del ancho de banda
El parámetro bandwidth tiene un impacto significativo en los resultados de la agrupación. Afinémoslo para ver si encontramos los cinco grupos. Probaremos tres valores diferentes de ancho de banda y visualizaremos los centros de conglomerados resultantes para cada uno de ellos.
# Try different bandwidth values
bandwidth_values = [0.1, 1.0, 2.0]
for bw in bandwidth_values:
ms = MeanShift(bandwidth=bw, bin_seeding=True)
ms.fit(X)
labels = ms.labels_
cluster_centers = ms.cluster_centers_
print("Bandwidth Value:", bw)
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='plasma', marker='p')
plt.scatter(cluster_centers[:, 0], cluster_centers[:, 1], s=250, c='blue', marker='X')
plt.title('mean shift clustering')
plt.xlabel('Attribute 1')
plt.ylabel('Attribute 2')
plt.show()
Agrupaciones de desplazamiento medio con un valor de ancho de banda de 0,1. Imagen del autor
Agrupaciones de desplazamiento medio con valor de ancho de banda 1,0. Imagen del autor
Agrupaciones de desplazamiento medio con valor de ancho de banda 2,0. Imagen del autor
El valor de ancho de banda de 0,1 parece demasiado bajo, lo que hace que el algoritmo trate cada punto de datos como un conglomerado independiente. Por otra parte, un valor de ancho de banda de 2,0 parece algo elevado, ya que no separó los dos conglomerados en nuestro primer intento. Un valor de ancho de banda de 1,0 resulta ser el más óptimo, revelando claramente los cinco conglomerados y sus centros.
Seleccionemos este valor y visualicemos los resultados una vez más.
ms = MeanShift(bandwidth=1.0, bin_seeding=True)
ms.fit(X)
labels = ms.labels_
cluster_centers = ms.cluster_centers_
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='plasma', marker='p')
plt.scatter(cluster_centers[:, 0], cluster_centers[:, 1], s=250, c='blue', marker='X')
plt.title('mean shift clustering')
plt.xlabel('Attribute 1')
plt.ylabel('Attribute 2')
plt.show()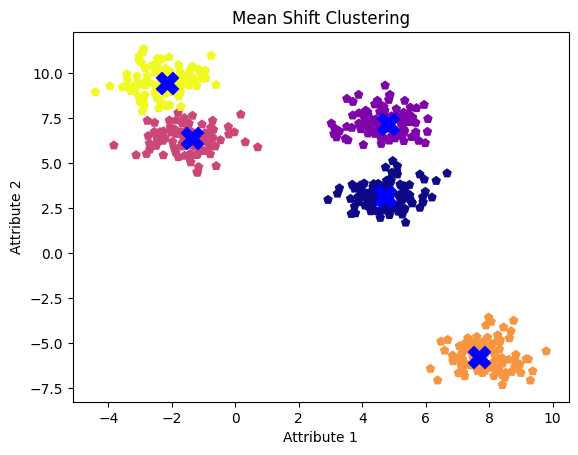
Conglomerados de desplazamiento medio con valor de ancho de banda de 1,0
Como se ha observado, un ancho de banda menor tiende a producir más agrupaciones, mientras que un ancho de banda mayor puede llevar a la fusión de agrupaciones.
Comparación del desplazamiento de la media con k-means
Comparemos los resultados del desplazamiento de medias y de la agrupación de k-means en el mismo conjunto de datos. En primer lugar, importa KMeans del módulo cluster de sklearn. A continuación, fijaremos el número de conglomerados en tres y ajustaremos el modelo para obtener los centroides de los conglomerados.
from sklearn.cluster import KMeans
# Perform k-means Clustering
kmeans = KMeans(n_clusters=3, random_state=0, n_init='auto')
kmeans.fit(X)
kmeans_labels = kmeans.labels_
kmeans_centers = kmeans.cluster_centers_Ahora, vamos a visualizar los resultados para compararlos con los de la agrupación por desplazamiento de la media.
plt.scatter(X[:, 0], X[:, 1], c=kmeans_labels, cmap='plasma', marker='p')
plt.scatter(kmeans_centers[:, 0], kmeans_centers[:, 1], s=250, c='red', marker='X')
plt.title('K-means Clustering')
plt.xlabel('Attribute 1')
plt.ylabel('Attribute 2')
plt.show()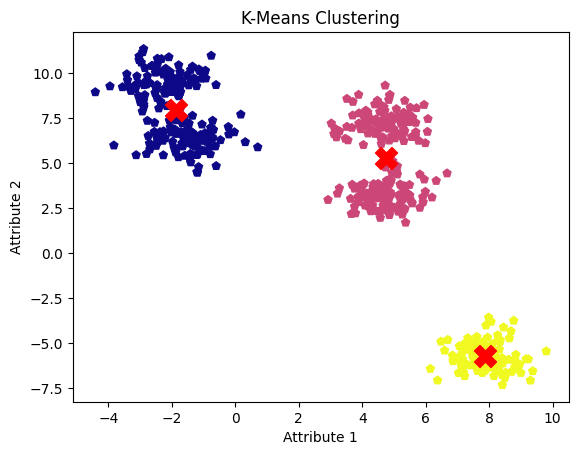
Resultados de la agrupación k-means. Imagen del autor
El inconveniente del algoritmo de agrupación k-means es que requiere especificar de antemano el número de conglomerados, lo que puede llevar a fusionar conglomerados adyacentes en uno solo. Sin embargo, un modelo de agrupación por desplazamiento medio bien afinado identificó con éxito los cinco conglomerados y sus centros.
Casos prácticos reales
Además del reconocimiento de objetos en el procesamiento de imágenes, la agrupación por desplazamiento medio se utiliza en una serie de aplicaciones del mundo real en múltiples dominios:
- Apoya el análisis de la expresión génica y la predicción de la estructura de las proteínas en bioinformática.
- Los analistas geoespaciales lo aprovechan para la agrupación geográfica y la detección de anomalías en los datos espaciales.
- En imagen médica, se utiliza para detectar tumores en resonancias magnéticas y tomografías computarizadas, así como para la clasificación de tejidos.
- El sector financiero lo utiliza para segmentar el mercado y detectar fraudes.
- Además, en el procesamiento del lenguaje natural (PLN), se aplica a la agrupación de documentos y al análisis de sentimientos.
Conclusión
En este post, aprendimos cómo la agrupación por desplazamiento medio se adapta a formas y tamaños de conglomerados variables, todo ello sin necesidad de un número predefinido de conglomerados.
Con todos los conocimientos y la aplicación práctica de este algoritmo, ya estás preparado para experimentarlo en tus proyectos. Python es el lenguaje de programación más popular, y merece la pena aprenderlo. Puedes consultar este itinerario profesional de Desarrollador Python para llevar tus conocimientos de programación en Python al siguiente nivel. Además, consulta nuestro itinerario profesional completo de Científico de Aprendizaje Automático con Python, y aprende de los expertos.
Conviértete en un Científico ML
¿Qué es la agrupación por desplazamiento medio?
¿En qué se diferencia la agrupación por desplazamiento de medias de k-means?
¿Cuáles son las aplicaciones reales de la agrupación por desplazamiento medio?
¿Cómo se selecciona el parámetro de ancho de banda en la agrupación por desplazamiento de medias?
¿Cuáles son los pasos clave para implementar la agrupación por desplazamiento medio en Python?
tutorial
Introducción a k-Means Clustering con scikit-learn en Python
Kevin Babitz
21 min
tutorial
Tutorial de K-Means Clustering en R
Eugenia Anello
17 min
tutorial
Clasificación K vecinos más próximos (KNN) con scikit-learn
Adam Shafi
14 min
tutorial
Introducción al t-SNE
Abid Ali Awan
14 min
tutorial
Búsqueda binaria en Python: guía completa para una búsqueda eficiente
Amberle McKee
12 min
tutorial
Aprendizaje automático de datos categóricos con el tutorial de Python
Moez Ali
28 min