Media aritmética: Una herramienta fundamental para el análisis de datos

La media aritmética, comúnmente conocida como "la media", suele ser el punto de partida en estadística descriptiva. Proporciona una medida rápida e intuitiva de la tendencia central, que es una parte esencial de la interpretación de datos en cualquier campo. Aunque el concepto pueda parecer sencillo, comprender los matices de la media aritmética puede revelar verdaderos conocimientos sobre tendencias y patrones de datos más complejos.

Este artículo ofrece una visión general de la media aritmética, cubriendo su fórmula, aplicaciones y comparaciones con otros tipos de medias. Examinaremos por qué se utiliza con frecuencia en economía, ciencia de datos y otros campos, al tiempo que analizaremos escenarios en los que otras medidas alternativas podrían ser más adecuadas.

Para los que se inician en la estadística o quieren afianzar sus conocimientos, nuestro curso de Introducción a la Estadística proporciona una gran base. Nuestra Ficha de Estadística Descriptiva también proporciona un útil glosario de términos relacionados con este tema.

¿Qué es la media aritmética?

La media aritmética es la suma de todos los números de un conjunto de datos dividida por el recuento de esos números. Este sencillo cálculo la convierte en una de las medidas de tendencia central más intuitivas y utilizadas.

Para ilustrarlo, veamos un ejemplo sencillo. Supongamos que tenemos tres números: 5, 10 y 15. Para calcular su media aritmética:

1. Suma los números: 5 + 10 + 15 = 30
2. Cuenta los números: Tenemos 3 números
3. Divide la suma por el recuento: 30 ÷ 3 = 10

Así, la media aritmética de 5, 10 y 15 es 10.

Propiedades clave de la media aritmética

La media aritmética posee varias propiedades importantes que resultan más intrigantes si se examinan más de cerca. 

La suma de las desviaciones es igual a cero

Una propiedad fundamental de la media aritmética es que la suma de las desviaciones respecto a ella siempre es igual a cero. En otras palabras, si restas el valor medio de cada punto de datos y sumas estas diferencias, el resultado será cero. Matemáticamente, esto puede expresarse como:

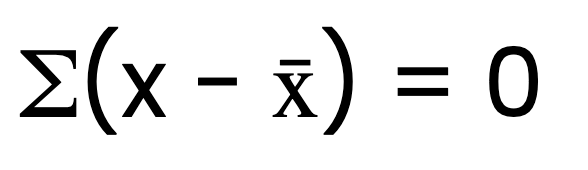
Donde x representa cada valor del conjunto de datos, y x̄ es la media aritmética.

Sensibilidad a los valores atípicos

En conjuntos de datos con valores extremos, la media aritmética puede acercarse mucho a estos valores atípicos, lo que puede llevar a interpretaciones erróneas, especialmente en distribuciones sesgadas. Por ejemplo, considera un conjunto de datos de salarios en una pequeña empresa: {$30,000, $35,000, $40,000, $45,000, $1,000,000}. La media aritmética (230.000 $) es significativamente superior a la mayoría de los salarios debido al valor atípico de 1.000.000 $.

Esta sensibilidad hace que la media aritmética sea menos robusta que medidas como la mediana en presencia de valores atípicos o para distribuciones sesgadas. Sin embargo, también puede hacer que la media sea útil para detectar la presencia de valores atípicos o comprender el impacto de los valores extremos en un conjunto de datos.

Impacto de los cambios en los datos

La media aritmética responde de forma predecible a los cambios en el conjunto de datos, lo que puede ser útil en diversos escenarios analíticos:

1. Sumar o restar una constante: Si sumas o restas el mismo valor de cada punto de datos, la media aumentará o disminuirá en esa cantidad exacta. Por ejemplo, si añades 5 a cada valor de un conjunto de datos, la nueva media será 5 más que la media original.
2. Multiplicar o dividir por una constante: Si multiplicas o divides cada punto de datos por la misma constante distinta de cero, la media se multiplicará o dividirá por esa constante. Por ejemplo, si duplicas todos los valores de un conjunto de datos, la nueva media será el doble de la media original.

Estas propiedades hacen que la media aritmética sea especialmente útil en situaciones que implican cambios uniformes en un conjunto de datos, como el ajuste de la inflación en datos económicos o el escalado de medidas en experimentos científicos.

Cuándo utilizar la media aritmética

La media aritmética es una herramienta estadística versátil, pero es especialmente eficaz en determinadas situaciones. En primer lugar, debemos decir que la media aritmética es especialmente útil para los conjuntos de datos que implican procesos aditivos. Por ejemplo, si calculas la temperatura media diaria, el salario medio en una empresa o la puntuación media en un examen, la media aritmética proporciona una representación significativa del valor central.

Además, debemos decir que la media aritmética es más fiable cuando los puntos de datos están distribuidos uniformemente, y no hay valores atípicos extremos. Veamos algunos ejemplos específicos del sector:

• Finanzas: En finanzas, las empresas se basan en la media aritmética para obtener información y establecer puntos de referencia. Por ejemplo, las empresas lo utilizan para determinar los salarios medios, los gastos mensuales y los beneficios trimestrales.
• Economía: Los economistas utilizan la media aritmética para analizar las tendencias del consumo y la estabilidad de los precios. Las aplicaciones clave incluyen el cálculo del consumo medio de los hogares y la creación de índices como el Índice de Precios al Consumo (IPC) para controlar la inflación a lo largo del tiempo.
• Sanidad e Investigación Médica: En sanidad, la media aritmética desempeña un papel fundamental en la evaluación de los tratamientos y el estudio de las tendencias sanitarias. Por ejemplo, los investigadores calculan los tiempos medios de recuperación y la eficacia de los fármacos, mientras que los epidemiólogos evalúan las tasas medias de infección y los tiempos de supervivencia.

Cómo calcular la media aritmética

Aunque ya hemos cubierto el concepto básico, vamos a explorar cómo calcular la media aritmética utilizando herramientas como R, Python y Excel, que es prácticamente necesario para conjuntos de datos más grandes.

Fórmula de la media aritmética

La fórmula de la media aritmética es:

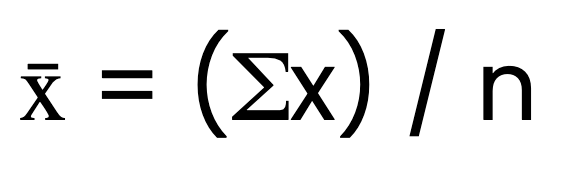
Donde x̄ es la media aritmética, Σx es la suma de todos los valores, y n es el número de valores.

Media aritmética en Excel, Python y R

Para conjuntos de datos más grandes, las herramientas informáticas facilitan mucho el cálculo. He aquí cómo calcular la media aritmética en Excel, Python y R. 

Excel

En Excel, puedes utilizar la función AVERAGE():

1. Introduce tus datos en una columna o fila.

2. En una nueva celda, escribe =AVERAGE().

3. Selecciona el rango de celdas que contiene tus datos.

4. Cierra el paréntesis y pulsa Introduce.

Por ejemplo, si tus datos están en las celdas A1:A10, utilizarías: =AVERAGE(A1:A10).

Python

El módulo estadístico de Python proporciona una función mean():

from statistics import mean

data = [5, 10, 15, 20, 25]

result = mean(data)
print(result)  # Output: 15

Para conjuntos de datos más grandes, quizá prefieras la función mean() de NumPy, más eficiente:

import numpy as np

data = np.array([5, 10, 15])

result = np.mean(data)
print(result)  # Output: 10.0

R

En R, puedes utilizar la función incorporada mean() de la base R:

data <- c(5, 10, 15)

result <- mean(data)
print(result)  # Output: [1] 10

Estas herramientas agilizan el proceso de cálculo de la media aritmética para conjuntos de datos de cualquier tamaño, permitiéndote centrarte en la interpretación de los datos en lugar del cálculo manual.

Media aritmética en ciencia de datos, aprendizaje automático y estadística

Las aplicaciones de la media aritmética en la ciencia de datos y el aprendizaje automático abarcan desde el preprocesamiento de datos hasta la evaluación de modelos. Exploremos algunas áreas clave en las que la media aritmética es especialmente importante. 

Escalado de características

Una de las aplicaciones más comunes de la media aritmética en el preprocesamiento de datos es el escalado de características, sobre todo en el centrado de medias:

• Centrado medio: Este proceso consiste en restar la media aritmética de cada punto de datos de una característica. El resultado es un conjunto de datos centrado en el que la media de cada característica es cero. Se puede representar como: x_centered = x - x̄ donde x es el valor original y x̄ es la media aritmética de la característica.

• Normalización: Utilizada a menudo junto con el centrado de la media, la normalización consiste en dividir por la desviación típica después de restar la media: x_standardized = (x - x̄) / σ donde σ es la desviación típica de la característica.

Estas técnicas ayudan a normalizar la escala de las características, lo que es especialmente importante para muchos algoritmos de aprendizaje automático. Si quieres saber más sobre la diferencia entre normalización y estandarización, puedes explorar el tutorial completo.

Evaluación del modelo

La media aritmética es fundamental en varias métricas de evaluación de modelos:

• Error cuadrático medio (ECM): Esta métrica habitual en los problemas de regresión calcula la media de las diferencias al cuadrado entre los valores predichos y los reales.
• Error medio absoluto (MAE): Similar al MSE, pero utiliza la diferencia absoluta en lugar de la diferencia al cuadrado.
• Precisión: En los problemas de clasificación, la precisión se suele expresar como la media de predicciones correctas en todas las muestras.

Estadística y comprobación de hipótesis

En el análisis estadístico, la media aritmética se utiliza a menudo en la comprobación de hipótesis. Por ejemplo:

• Pruebas T: La media aritmética es crucial en las pruebas t, que comparan las medias de dos grupos para determinar si son estadísticamente diferentes. Al comparar las medias muestrales, las pruebas t ayudan a validar las hipótesis sobre las características de la población.
• Intervalos de confianza: La media aritmética se utiliza para calcular los intervalos de confianza, que indican la fiabilidad de la media estimada. Esto da una idea de lo representativa que es la media de la muestra para toda la población.

Otras aplicaciones

• Métodos de conjunto: Muchas técnicas de ensemble, como el bagging y el boosting, utilizan la media aritmética para combinar las predicciones de varios modelos.
• Descenso Gradiente: La media aritmética se utiliza para calcular el gradiente medio entre minilotes en el descenso de gradiente estocástico.
• Detección de anomalías: Las desviaciones de la media pueden utilizarse para identificar valores atípicos o anomalías en los conjuntos de datos. Por ejemplo, una heurística habitual es utilizar tres desviaciones típicas como umbral, de modo que cualquier punto de datos que se aleje tres o más desviaciones típicas de la media aritmética se consideraría un valor atípico.
• Reducción de la dimensionalidad: Técnicas como el análisis de componentes principales (ACP) utilizan la media aritmética en sus cálculos para centrar los datos antes de calcular la matriz de covarianzas.
• Redes neuronales: En el algoritmo de retropropagación, se utiliza la media aritmética para calcular el error medio entre los ejemplos de entrenamiento.
• Validación cruzada: Cuando se realiza una validación cruzada de k pliegues, la media aritmética de las métricas de rendimiento de todos los pliegues suele indicarse como estimación del rendimiento global.

Como ya te habrás dado cuenta, la media aritmética es importante tanto para interpretar el resultado de los datos como para realizar un preprocesamiento necesario para el rendimiento óptimo del modelo. Para profundizar en el conocimiento de estos conceptos y sus aplicaciones prácticas, considera la posibilidad de cursar nuestro itinerario profesional de Científico de Aprendizaje Automático en Python, que cubre estos temas en mayor profundidad.