Curso
Preparar con precisión tus datos es importante tanto para el funcionamiento de los modelos como para la interpretación de los resultados. Éste es el reto central en el que entran en juego la normalización y la estandarización, dos técnicas esenciales de escalado de características que pueden utilizarse para ajustar los datos para obtener un mejor rendimiento o ayudar en la interpretación de los resultados.
En este artículo, te guiaré a través de los diferentes términos y también te ayudaré a ver algo de las diferencias prácticas entre normalización y estandarización. Al final, sabrás cuándo utilizar cada uno de ellos en tu flujo de trabajo de preprocesamiento de datos. Al familiarizarte con la normalización y la estandarización, aumentarás el rendimiento de tus modelos, interpretarás mejor los resultados y evitarás los errores comunes que conllevan los datos sin escalar. Las sutiles diferencias aquí son muy importantes en el campo del aprendizaje automático. Si te tomas en serio lo de convertirte en un experto, inscríbete hoy mismo en nuestro itinerario profesional de Científico de Aprendizaje Automático en Python.
Conviértete en un Científico ML
Comprender el escalado de funciones
Tanto la normalización como la estandarización pertenecen a la idea o categoría de escalado de rasgos. El escalado de rasgos es un paso importante en la preparación de los datos para los modelos de aprendizaje automático. Consiste en transformar los valores de las características de un conjunto de datos a una escala similar, garantizando que todas las características contribuyan por igual al proceso de aprendizaje del modelo.
El escalado de rasgos es importante porque, cuando los rasgos están en escalas muy diferentes, como un rasgo que va de 1 a 10 y otro de 1.000 a 10.000, los modelos pueden dar prioridad a los valores más grandes, lo que provoca un sesgo en las predicciones. Esto puede provocar un rendimiento deficiente del modelo y una convergencia más lenta durante el entrenamiento.
El escalado de rasgos aborda estos problemas ajustando el rango de los datos sin distorsionar las diferencias en los valores. Existen varias técnicas de escalado, siendo la normalización y la estandarización las más utilizadas. Ambos métodos ayudan a los modelos de aprendizaje automático a funcionar de forma óptima equilibrando el impacto de las características, reduciendo la influencia de los valores atípicos y, en algunos casos, mejorando las tasas de convergencia.
¿Qué es la Normalización?
La normalización es una idea amplia, y hay diferentes formas de normalizar los datos. En términos generales, la normalización se refiere al proceso de ajustar los valores medidos en diferentes escalas a una escala común. A veces, es mejor ilustrarlo con un ejemplo. A continuación, para cada tipo de normalización, consideraremos un modelo para comprender la relación entre el precio de una vivienda y su tamaño.
Tipos de normalización
Veamos algunos de los principales tipos. Ten en cuenta que no es una lista exhaustiva:
Normalización mín-máx
Con la normalización mín-máx, podríamos reescalar los tamaños de las casas para que se ajusten a un intervalo de 0 a 1. Esto significa que el tamaño de casa más pequeño se representaría como 0, y el tamaño de casa más grande se representaría como 1.
Normalización logarítmica
La normalización logarítmica es otra técnica de normalización. Mediante la normalización logarítmica, aplicamos una transformación logarítmica a los precios de la vivienda. Esta técnica ayuda a reducir el impacto de los precios más altos, sobre todo si hay diferencias significativas entre ellos.
Escala decimal
La escala decimal es otra técnica de normailzación. Para este ejemplo, podríamos ajustar los tamaños de las casas desplazando el punto decimal para hacer los valores más pequeños. Esto significa que los tamaños de las casas se transforman a una escala más manejable, manteniendo intactas sus diferencias relativas.
Normalización de la media (centrado de la media)
La normalización de la media, en este contexto, implicaría ajustar los precios de la vivienda restando el precio medio del precio de cada vivienda. Este proceso centra los precios en cero, mostrando cómo se compara el tamaño de cada casa con la media. Al hacerlo, podemos analizar qué tamaños de casa son mayores o menores que la media, lo que facilita la interpretación de sus precios relativos.
¿Cuándo debes normalizar los datos?
Como habrás deducido de los ejemplos anteriores, la normalización es especialmente útil cuando la distribución de los datos es desconocida o no sigue una distribución gaussiana. El precio de la vivienda es un buen ejemplo, porque algunas casas son muy, muy caras, y los modelos no siempre se adaptan bien a los valores atípicos.
Por tanto, el objetivo de la normalización es hacer un modelo mejor. Podríamos normalizar la variable dependiente para que los errores se distribuyan de forma más uniforme, o bien normalizar las variables de entrada para asegurarnos de que los rasgos con escalas mayores no dominen a los que tienen escalas menores.
La normalización es más eficaz en los siguientes casos:
- Distribución desconocida o no gaussiana: Cuando la distribución de los datos no se conoce o no sigue un patrón normal (gaussiano). Por ejemplo, en la regresión lineal, puede que queramos normalizar la variable dependiente para que se parezca más a una curva de campana, lo que permite una mayor confianza en nuestras estimaciones.
- Algoritmos basados en la distancia: La normalización es necesaria cuando se utilizan algoritmos de aprendizaje automático que se basan en distancias entre puntos de datos, como k-Nearest Neighbors (k-NN), para evitar que los rasgos con escalas mayores dominen los cálculos de distancia.
¿Qué es la Normalización?
Mientras que la normalización escala las características a un rango específico, la estandarización, que también se llama escala de puntuación z, transforma los datos para que tengan una media de 0 y una desviación típica de 1. Este proceso ajusta los valores de las características restando la media y dividiendo por la desviación típica. Puede que hayas oído hablar de "centrar y escalar" datos. Pues bien, la normalización se refiere a lo mismo: primero centrar, luego escalar.
La fórmula de la normalización es
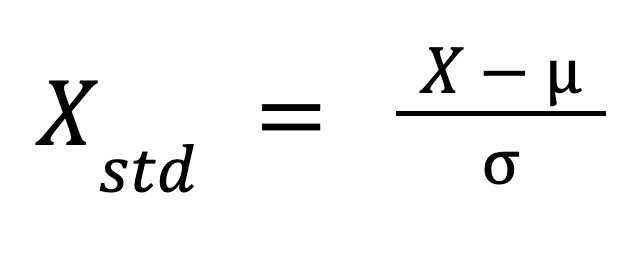
Dónde:
- X es el valor original,
- mu es la media de la característica, y
- sigma es la desviación típica de la característica.
Esta fórmula reescala los datos de forma que su distribución tenga una media de 0 y una desviación típica de 1.
¿Cuándo debes normalizar los datos?
La normalización es más adecuada en los siguientes casos:
- Algoritmos basados en el gradiente: La máquina de vectores de apoyo (SVM) requiere datos normalizados para un rendimiento óptimo. Aunque los modelos como la regresión lineal y la regresión logística no asumen la normalización, pueden beneficiarse de ella, sobre todo cuando las características varían mucho en magnitud, lo que ayuda a garantizar contribuciones equilibradas de cada característica y a mejorar la optimización.
- Reducción de la dimensionalidad: La normalización está en las técnicas de reducción de la dimensionalidad, como el ACP, porque el ACP identifica la dirección en la que se maximiza la varianza de los datos. La normalización de la media por sí sola no es suficiente, porque el ACP considera tanto la media como la varianza, y diferentes escalas de rasgos distorsionarían el análisis.
Normalización vs. Normalización: Diferencias clave
A veces, es difícil distinguir entre normalización y estandarización. Por un lado, normalización se utiliza a veces como un término más general, mientras que normalización tiene un significado un poco más específico o específicamente técnico. Además, los analistas de datos y los científicos de datos que estén familiarizados con los términos podrían seguir teniendo dificultades para distinguir los casos de uso.
Aunque ambas son técnicas de escalado de características, difieren en sus planteamientos y aplicaciones. Comprender estas diferencias es clave para elegir la técnica adecuada para tu modelo de aprendizaje automático.
Métodos de reescalado
La normalización reescala los valores de los rasgos dentro de un intervalo predefinido, a menudo entre 0 y 1, lo que resulta especialmente útil para modelos en los que la escala de los rasgos varía mucho. En cambio, la normalización centra los datos en torno a la media (0) y los escala según la desviación típica (1).
Sensibilidad a los valores atípicos
Las distintas técnicas de normalización varían en su eficacia para tratar los valores atípicos. La normalización de la media puede ajustar con éxito los valores atípicos en algunos escenarios, pero otras técnicas pueden no ser tan eficaces. En general, las técnicas de normalización no tratan el problema de los valores atípicos con tanta eficacia como la normalización, porque ésta se basa explícitamente tanto en la media como en la desviación típica.
Casos prácticos
La normalización se utiliza mucho en algoritmos basados en la distancia, como k-Nearest Neighbors (k-NN), en los que las características deben estar en la misma escala para garantizar la precisión en los cálculos de distancia. La normalización, por otra parte, es vital para los algoritmos basados en el gradiente, como las Máquinas de Vectores de Soporte (SVM), y se aplica con frecuencia en las técnicas de reducción de la dimensionalidad, como el PCA, donde es importante mantener la varianza correcta de las características.
Tabla resumen de diferencias
Veamos todas estas diferencias clave en una tabla resumen para facilitar la comparación entre normalización y estandarización:
| Categoría | Normalización | Normalización |
|---|---|---|
| Método de reescalado | Escala los datos a un intervalo (normalmente de 0 a 1) basándose en los valores mínimo y máximo. | Centra los datos alrededor de la media (0) y los escala por la desviación típica (1). |
| Sensibilidad a los valores atípicos | La normalización puede ayudar a ajustar los valores atípicos si se utiliza correctamente, dependiendo de la técnica. | La normalización es un enfoque más coherente para solucionar los problemas de los valores atípicos. |
| Algoritmos comunes | A menudo se aplica en algoritmos como k-NN y redes neuronales que requieren que los datos estén a una escala consistente. | Es el más adecuado para algoritmos que requieren que las características tengan una escala común, como la regresión logística, la SVM y el PCA. |
Visualizar las diferencias
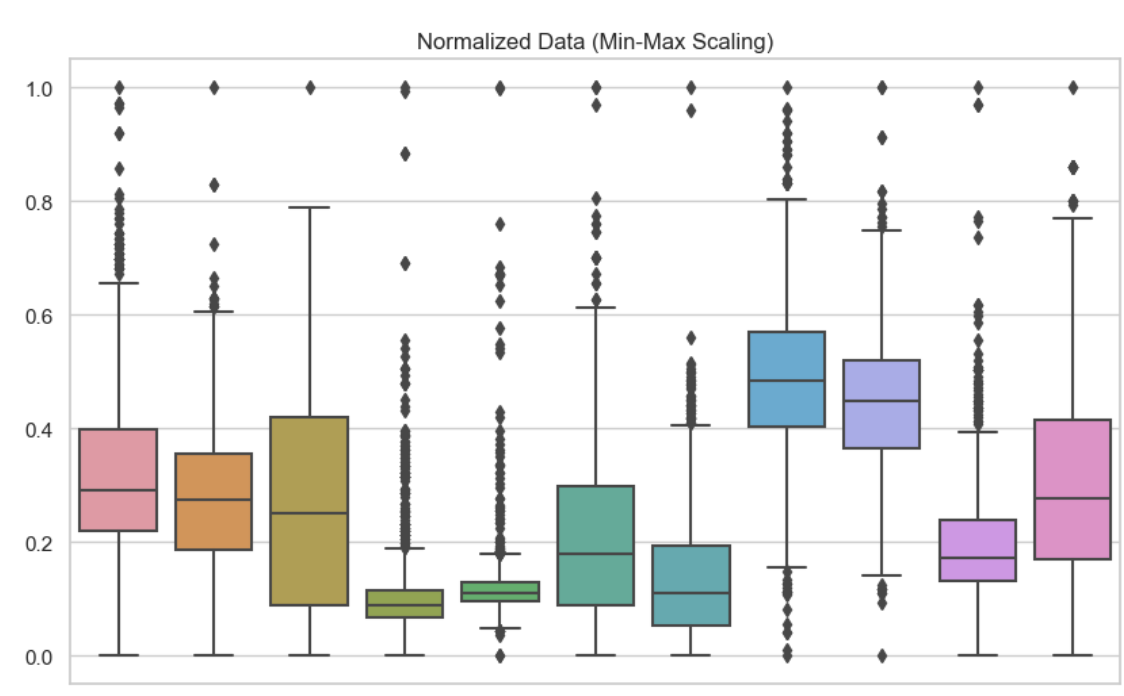
Para comprender las diferencias entre normalización y estandarización, es útil ver sus efectos visualmente y en términos de rendimiento del modelo. Aquí he incluido gráficos de caja para mostrar estas diferentes técnicas de escalado de rasgos. Aquí he utilizado la normalización mín-máx en cada una de las variables de mi conjunto de datos. Podemos ver que ningún valor es menor que 0 ni mayor que 1.
Datos normalizados. Imagen del autor
En este segundo visual, he utilizado la estandarización en cada una de las variables. Podemos ver que los datos están centrados en cero.
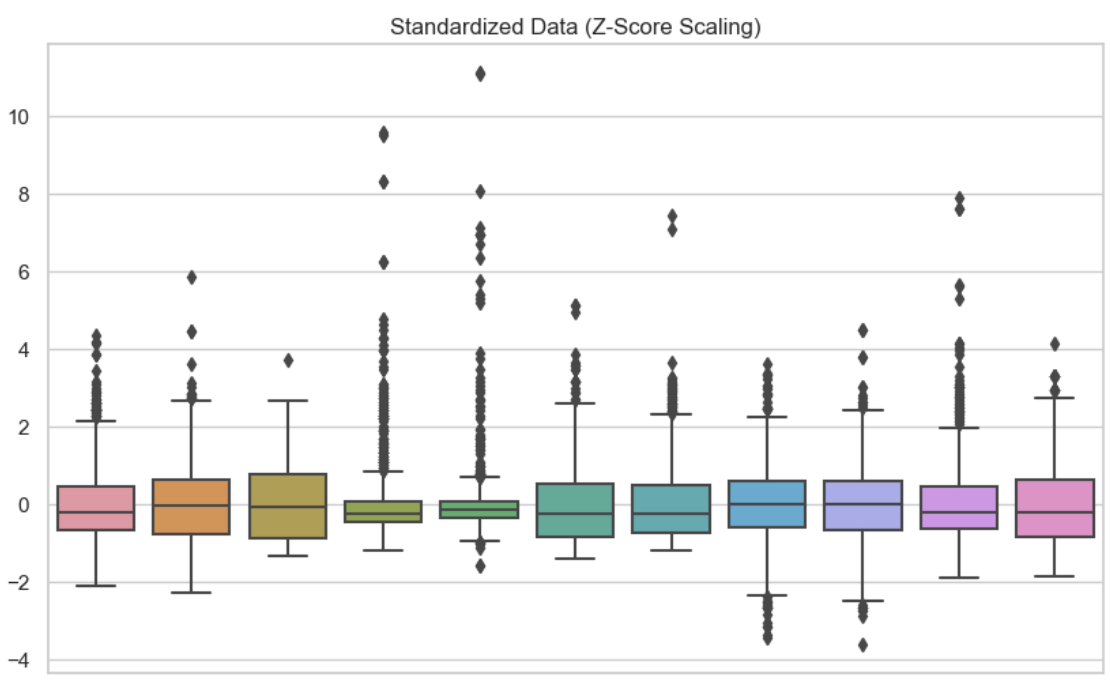 Datos Datos normalizados. Imagen del autor
Datos Datos normalizados. Imagen del autor
Ventajas y desventajas
Las ventajas incluyen un mejor rendimiento del modelo y una contribución equilibrada de los rasgos. Sin embargo, la normalización puede limitar la interpretabilidad debido a la escala fija, mientras que la normalización también puede dificultar la interpretación, pues los valores ya no reflejan sus unidades originales. Siempre hay un equilibrio entre la complejidad y la precisión del modelo.
Normalización y estandarización en regresión lineal
Consideremos cómo la normalización (en este caso, la normalización de la media) y la estandarización pueden cambiar la interpretación de un modelo de regresión lineal simple. El R-cuadrado o el R-cuadrado ajustado sería el mismo para cada modelo, por lo que el escalado de características aquí sólo se refiere a la interpretación de nuestro modelo.
| Transformación Aplicada | Variable independiente (Tamaño de la casa) | Variable dependiente (Precio de la vivienda) | Interpretación |
|---|---|---|---|
| Normalización de la media | Media Normalizada | Original | Estás prediciendo el precio original de la vivienda para cada cambio de tamaño de la vivienda en relación con la media. |
| Normalización | Normalizado | Original | Estás prediciendo el precio original de la casa para cada cambio de una desviación típica en el tamaño de la casa. |
| Normalización de la media | Original | Media Normalizada | Estás prediciendo el precio de la vivienda en relación con la media para cada aumento de una unidad en el tamaño original de la vivienda. |
| Normalización | Original | Normalizado | Estás prediciendo el precio estandarizado de la vivienda para cada aumento de una unidad en el tamaño original de la vivienda. |
| Normalización de la media (ambas variables) | Media Normalizada | Media Normalizada | Estás prediciendo el precio de la vivienda respecto a la media para cada cambio en el tamaño de la vivienda respecto a la media. |
| Normalización (ambas variables) | Normalizado | Normalizado | Estás prediciendo el precio estandarizado de la vivienda para cada cambio de una desviación típica en el tamaño de la vivienda. |
Como otra nota importante, en la regresión lineal, si estandarizas las variables independiente y dependiente, la r-cuadrado seguirá siendo la misma. Esto se debe a que la r-cuadrado mide la proporción de la varianza en y que es explicada por x, y esta proporción sigue siendo la misma independientemente de si las variables están estandarizadas o no. Sin embargo, estandarizar la variable dependiente cambiará el RMSE, porque el RMSE se mide en las mismas unidades que la variable dependiente. Como ahora y está normalizado, el RMSE será menor tras la normalización. Concretamente, reflejará el error en términos de la desviación típica de la variable estandarizada, no de las unidades originales. Si la regresión te interesa especialmente, sigue nuestro curso Introducción a la regresión con modelos estadísticos en Python para convertirte en un experto.
Conclusión
El escalado de características, que incluye la normalización y la estandarización, es un componente crítico del preprocesamiento de datos en el aprendizaje automático. Comprender los contextos adecuados para aplicar cada técnica puede mejorar significativamente el rendimiento y la precisión de tus modelos.
Si quieres ampliar y profundizar tus conocimientos sobre el escalado de características y su papel en el aprendizaje automático, en DataCamp tenemos varios recursos excelentes que pueden ayudarte a empezar. Puedes explorar nuestro artículo sobre la Normalización en el Aprendizaje Automático para conocer los conceptos básicos, o considerar nuestro curso de Aprendizaje Automático End-to-End, que cubre aplicaciones reales.
Conviértete en un Científico ML
Escritora y profesional de los datos con experiencia a la que le apasiona capacitar a los aspirantes a expertos en el espacio de los datos.