Arbres de décision dans l'apprentissage automatique à l'aide de R

Imaginez-vous en train de naviguer dans un labyrinthe. À chaque pas, vous êtes confronté à une décision qui vous rapproche de la sortie ou vous enfonce dans le labyrinthe. Cela s'apparente à un algorithme d'arbre de décision, une méthode d'apprentissage automatique puissante et intuitive qui nous aide à donner un sens à des données complexes et à choisir le meilleur plan d'action.

Un algorithme d'arbre de décision décompose un ensemble de données en sous-ensembles de plus en plus petits sur la base de certaines conditions. Comme un arbre à feuilles et à nœuds, il commence par un nœud racine unique et se développe en plusieurs branches, chacune représentant une décision basée sur la valeur d'une caractéristique. Les dernières feuilles de l'arbre sont les résultats possibles ou les prédictions.

Cet article vous introduira au monde des arbres de décision en utilisant le langage de programmation R. Nous aborderons les principes de base, les types d'algorithmes d'arbres de décision les plus courants, les méthodes basées sur les arbres et nous vous présenterons un exemple étape par étape. À la fin, vous serez en mesure d'exploiter la puissance des arbres de décision pour prendre de meilleures décisions fondées sur des données.

Qu'est-ce qu'un arbre de décision dans l'apprentissage automatique ?

Les arbres de décision sont des outils particuliers de l'apprentissage automatique en raison de leur simplicité, de leur facilité d'interprétation et de leur polyvalence.

Il s'agit d'un algorithme d'apprentissage automatique supervisé qui peut être utilisé pour les problèmes de régression (prédiction de valeurs continues) et de classification (prédiction de valeurs catégorielles). En outre, ils servent de base à des techniques plus avancées, telles que le bagging, le boosting et les forêts aléatoires.

Le diagramme ci-dessous illustre la terminologie des arbres de décision :

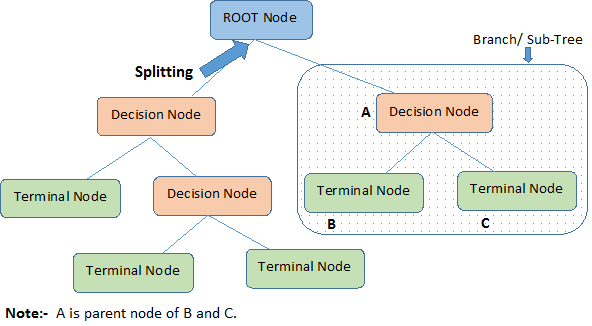
Un arbre de décision commence par un nœud racine qui représente l'ensemble de la population ou de l'échantillon, qui se sépare ensuite en deux groupes uniformes ou plus par le biais d'une méthode appelée "splitting". Lorsque les sous-nœuds subissent une nouvelle division, ils sont identifiés comme des nœuds de décision, tandis que ceux qui ne se divisent pas sont appelés nœuds terminaux ou feuilles. Un segment d'un arbre complet est appelé branche.

Nous avons établi que les arbres de décision pouvaient être utilisés à la fois pour les tâches de régression et de classification ; nous allons donc comprendre l'algorithme qui sous-tend les types d'arbres de décision.

Types populaires d'algorithmes d'arbres de décision

Comprenons intuitivement les arbres de décision de régression et de classification, leurs similitudes et leurs différences, ainsi que les fonctions d'erreur.

Arbres de régression

Examinons l'image ci-dessous, qui permet de visualiser la nature du partitionnement effectué par un arbre de régression. Ceci montre un arbre non élagué et un arbre de régression adapté à un ensemble de données aléatoires. Les deux visualisations montrent une série de règles de division, en commençant par le sommet de l'arbre. Vous remarquerez que chaque partie du domaine est alignée sur l'un des axes des caractéristiques. Le concept de division parallèle des axes se généralise directement aux dimensions supérieures à deux. Pour un espace de caractéristiques de taille $p$, un sous-ensemble de $\mathbb{R}^p$, l'espace est divisé en $M$ régions, $R_{m}$, chacune d'entre elles étant un "hyperbloc" de dimension $p$.

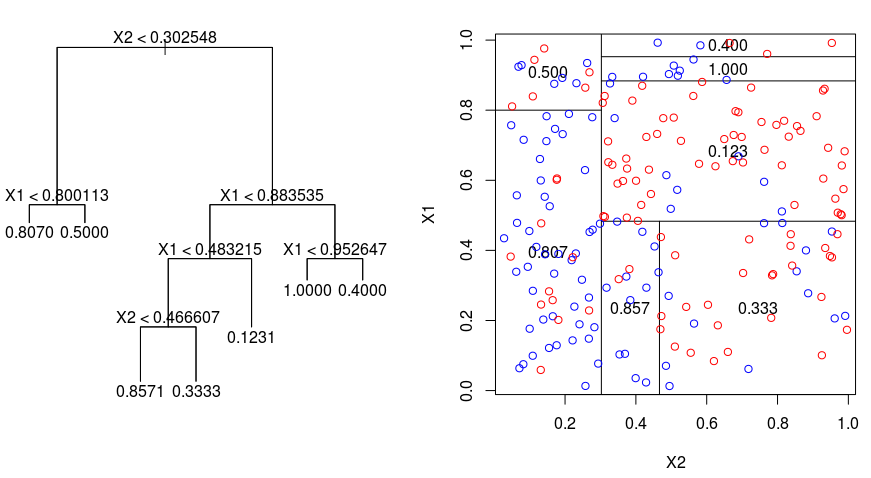
Pour construire un arbre de régression, vous utilisez d'abord la division binaire récursive pour faire croître un grand arbre sur les données d'apprentissage, en ne vous arrêtant que lorsque chaque nœud terminal a moins d'un certain nombre minimum d'observations. Le fractionnement binaire récursif est un algorithme gourmand et descendant utilisé pour minimiser la somme des carrés résiduels (RSS), une mesure d'erreur également utilisée dans les contextes de régression linéaire. Le RSS, dans le cas d'un espace de caractéristiques partitionné avec M partitions, est donné par la formule suivante :

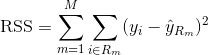
En partant du sommet de l'arbre, vous le divisez en deux branches, créant ainsi une partition de deux espaces. Vous effectuez ensuite plusieurs fois cette division particulière au sommet de l'arbre et choisissez la division des caractéristiques qui minimise le RSS (actuel).

Ensuite, vous appliquez l'élagage de complexité des coûts au grand arbre afin d'obtenir une séquence des meilleurs sous-arbres, en fonction de $\alpha$. L'idée de base est d'introduire un paramètre de réglage supplémentaire, désigné par $\alpha$, qui équilibre la profondeur de l'arbre et sa qualité d'adaptation aux données d'apprentissage.

Vous pouvez utiliser la validation croisée K-fold pour choisir $\alpha$. Cette technique consiste simplement à diviser les observations d'apprentissage en K plis afin d'estimer le taux d'erreur de test des sous-arbres. Votre objectif est de sélectionner celui qui conduit au taux d'erreur le plus bas.

Arbres de classification

Un arbre de classification est très similaire à un arbre de régression, sauf qu'il est utilisé pour prédire une réponse qualitative plutôt que quantitative.

Rappelons que pour un arbre de régression, la réponse prédite pour une observation est donnée par la réponse moyenne des observations d'apprentissage qui appartiennent au même nœud terminal. En revanche, dans le cas d'un arbre de classification, vous prédisez que chaque observation appartient à la classe d'observations de formation la plus fréquente dans la région à laquelle elle appartient.

Lorsque vous interprétez les résultats d'un arbre de classification, vous vous intéressez souvent non seulement à la prédiction de la classe correspondant à une région particulière du nœud terminal, mais aussi aux proportions de classes parmi les observations d'apprentissage qui tombent dans cette région.

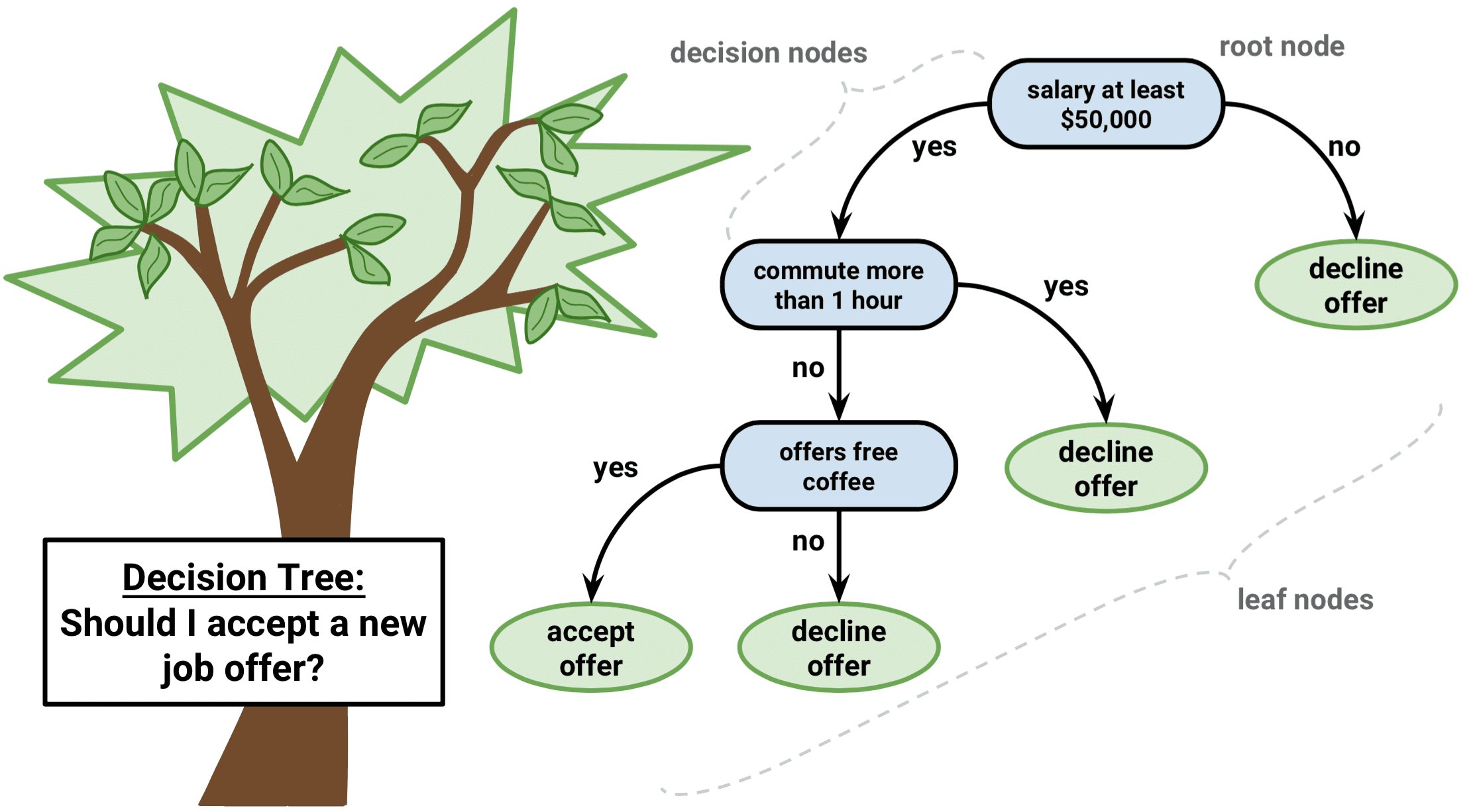
L'élaboration d'un arbre de classification est assez similaire à l'élaboration d'un arbre de régression. Tout comme dans le cadre de la régression, vous utilisez la division binaire récursive pour développer un arbre de classification. Toutefois, dans le cadre de la classification, la somme des carrés résiduels ne peut pas être utilisée comme critère pour effectuer les divisions binaires. Au lieu de cela, vous pouvez utiliser l'une des trois méthodes ci-dessous :

• Taux d'erreur de classification: Plutôt que de voir à quel point une réponse numérique est éloignée de la valeur moyenne, comme dans le cadre de la régression, vous pouvez définir le "taux de réussite" comme la fraction des observations d'entraînement dans une région particulière qui n'appartient pas à la classe la plus répandue. L'erreur est donnée par cette équation :

E = 1 - _argmaxc($hat{\pi}_{mc}$)

où $\hat{\pi}_{mc}$ représente la fraction des données d'apprentissage de la région _Rm qui appartiennent à la classe c.

• Indice de Gini: L'indice de Gini est une mesure d'erreur alternative conçue pour montrer le degré de "pureté" d'une région. Dans ce cas, le terme "pureté" désigne la proportion des données d'apprentissage d'une région donnée qui appartiennent à une seule classe. Si une région _Rm contient des données provenant principalement d'une seule classe c, la valeur de l'indice de Gini sera faible :

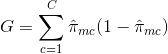
• L'entropie croisée: Une troisième solution, similaire à l'indice de Gini, est connue sous le nom d'entropie croisée ou de déviance :

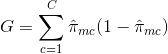
L'entropie croisée prendra une valeur proche de zéro si les $hat{\pi}_{mc}$ sont tous proches de 0 ou de 1. Par conséquent, comme l'indice de Gini, l'entropie croisée prendra une faible valeur si le mème nœud est pur. En fait, il s'avère que l'indice de Gini et l'entropie croisée sont assez proches numériquement.

Lors de la construction d'un arbre de classification, l'indice de Gini ou l'entropie croisée sont généralement utilisés pour évaluer la qualité d'une division particulière, car ils sont plus sensibles à la pureté des nœuds que le taux d'erreur de classification. Chacune de ces trois approches peut être utilisée lors de l'élagage de l'arbre, mais le taux d'erreur de classification est préférable si la précision de la prédiction de l'arbre final élagué est l'objectif.

Avantages et inconvénients des arbres de décision

Même si nous aimerions comprendre l'algorithme et ses points forts, il est essentiel de comprendre ses faiblesses. En réalité, les arbres de décision ne conviennent pas à tous les types d'algorithmes d'apprentissage automatique, ce qui est également le cas de tous les algorithmes d'apprentissage automatique.

Voici les avantages et les inconvénients :

Avantages

1. Facile à comprendre et à interpréter. Les arbres de décision sont très intuitifs et peuvent être facilement visualisés. Leur structure hiérarchique ressemble à la prise de décision humaine, ce qui les rend accessibles même aux non-experts. Cette capacité d'interprétation est cruciale dans les situations où la compréhension du processus de décision est tout aussi importante que la prédiction elle-même.
2. Peut traiter des variables continues et catégorielles. Les arbres de décision sont polyvalents et peuvent gérer des ensembles de données comportant un mélange de caractéristiques continues et catégorielles, ainsi que des variables cibles de l'un ou l'autre type. Cette flexibilité permet d'appliquer les arbres de décision à un large éventail de problèmes.
3. Un prétraitement minimal des données est nécessaire. Les arbres de décision ne nécessitent pas de mise à l'échelle ou de normalisation des caractéristiques, car ils sont invariants par rapport aux transformations monotones. Ils peuvent également traiter facilement les valeurs manquantes et les valeurs aberrantes, ce qui les rend adaptés aux données brutes et bruyantes.
4. Il peut être utilisé pour la sélection des caractéristiques et l'identification des variables importantes. Les arbres de décision effectuent naturellement une sélection des caractéristiques en choisissant les caractéristiques les plus informatives pour diviser les données. L'importance d'une caractéristique peut être déterminée en fonction de sa précocité dans l'arbre et de la fréquence à laquelle elle est utilisée pour le fractionnement.

Inconvénients

1. Sujet à des ajustements excessifs. Les arbres de décision peuvent devenir trop complexes lorsqu'ils deviennent profonds, ce qui entraîne un surajustement des données d'apprentissage. Il en résulte une mauvaise généralisation des données non vues. Des techniques telles que l'élagage ou la fixation d'une profondeur maximale peuvent contribuer à atténuer ce problème.
2. Sensible aux petits changements dans les données. Une petite modification des données d'apprentissage peut conduire à une arborescence complètement différente, ce qui rend les arbres de décision instables. Cette sensibilité peut être réduite par des méthodes d'ensemble, telles que le bagging, le boosting ou les forêts aléatoires, qui construisent plusieurs arbres et agrègent leurs résultats.
3. Les modèles d'arbres de décision ne sont souvent pas aussi précis que d'autres méthodes d'apprentissage automatique. En raison de leur simplicité et de la nature avide de leur construction, les arbres de décision ne produisent pas toujours les modèles les plus précis. Cependant, elles peuvent servir de point de départ ou de modèle de référence pour la comparaison avec des méthodes plus sophistiquées.
4. Parti pris en faveur des classes dominantes. Les arbres de décision peuvent être biaisés en faveur de la classe majoritaire dans les ensembles de données déséquilibrés, ce qui entraîne des scissions sous-optimales et une mauvaise classification des instances minoritaires. Des techniques telles que le suréchantillonnage, le sous-échantillonnage ou l'utilisation de l'apprentissage sensible aux coûts peuvent contribuer à résoudre ce problème.

Malgré ces inconvénients, les arbres de décision restent un choix populaire dans de nombreuses applications en raison de leur simplicité, de leur facilité d'interprétation et de leur polyvalence.

Algorithmes avancés d'apprentissage automatique basé sur les arbres

Examinons les méthodes d'ensemble basées sur les arbres qui tirent parti des atouts des arbres de décision tout en tenant compte de certaines de leurs limites : le bagging, le boosting et les forêts aléatoires.

Ensachage

Les arbres de décision évoqués ci-dessus souffrent d'une variance élevée, ce qui signifie que si vous divisez les données d'apprentissage en deux parties au hasard et que vous adaptez un arbre de décision aux deux moitiés, les résultats que vous obtiendrez pourraient être très différents. En revanche, une procédure à faible variance donnera des résultats similaires si elle est appliquée de manière répétée à un ensemble de données distinct.

Le bagging, ou agrégation bootstrap, est une technique utilisée pour réduire la variance de vos prédictions en combinant les résultats de plusieurs classificateurs modélisés sur différents sous-échantillons du même ensemble de données. Voici l'équation de l'ensachage :

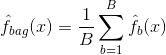
dans lequel vous générez $B$ différents ensembles de données d'apprentissage bootstrap. Vous entraînez ensuite votre méthode sur le $bth$ bootstrapped training set afin d'obtenir $\hat{f}_{b}(x)$, et enfin vous faites la moyenne des prédictions.

L'illustration ci-dessous montre les trois étapes de l'ensachage :

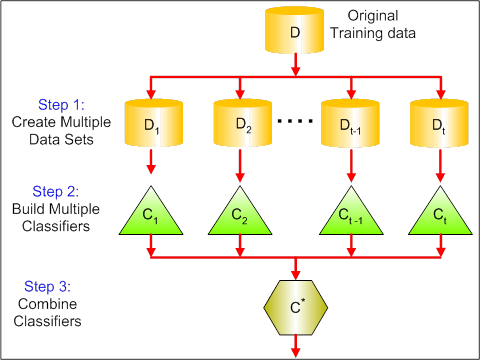
• Étape 1: Dans ce cas, vous remplacez les données d'origine par de nouvelles données. Les nouvelles données comportent généralement une fraction des colonnes et des lignes des données d'origine, qui peuvent alors être utilisées comme hyperparamètres dans le modèle de regroupement.

• Étape 2: Vous construisez des classificateurs sur chaque ensemble de données. En règle générale, vous pouvez utiliser le même classificateur pour établir des modèles et des prédictions.

• Étape 3: Enfin, vous utilisez une valeur moyenne pour combiner les prédictions de tous les classificateurs, en fonction du problème. En général, ces valeurs combinées sont plus robustes qu'un modèle unique.

Si l'ensachage permet d'améliorer les prédictions pour de nombreuses méthodes de régression et de classification, il est particulièrement utile pour les arbres de décision. Pour appliquer le bagging aux arbres de régression/classification, il suffit de construire $B$ arbres de régression/classification à l'aide de $B$ ensembles d'apprentissage bootstrapés, et de faire la moyenne des prédictions obtenues. Ces arbres sont cultivés en profondeur et ne sont pas taillés. Par conséquent, chaque arbre individuel présente une variance élevée, mais un faible biais. La moyenne de ces $B$ arbres réduit la variance.

D'une manière générale, il a été démontré que le bagging permettait d'améliorer considérablement la précision en combinant des centaines, voire des milliers d'arbres en une seule procédure.

Forêts aléatoires

Random Forests est une méthode d'apprentissage automatique polyvalente capable d'effectuer des tâches de régression et de classification. Il applique également des méthodes de réduction dimensionnelle, traite les valeurs manquantes, les valeurs aberrantes et d'autres étapes essentielles de l'exploration des données, et fait un assez bon travail.

Random Forests améliore les arbres ensachés grâce à une petite modification qui décorelle les arbres. Comme pour le bagging, vous construisez un certain nombre d'arbres de décision sur des échantillons de formation bootstrapés. Mais lors de la construction de ces arbres de décision, chaque fois qu'une division dans un arbre est envisagée, un échantillon aléatoire de m prédicteurs est choisi comme candidats à la division à partir de l'ensemble complet de $p$ prédicteurs. La division est autorisée à utiliser un seul de ces $m$ prédicteurs. C'est la principale différence entre les forêts aléatoires et le bagging, car comme dans le bagging, le choix du prédicteur $m = p$.

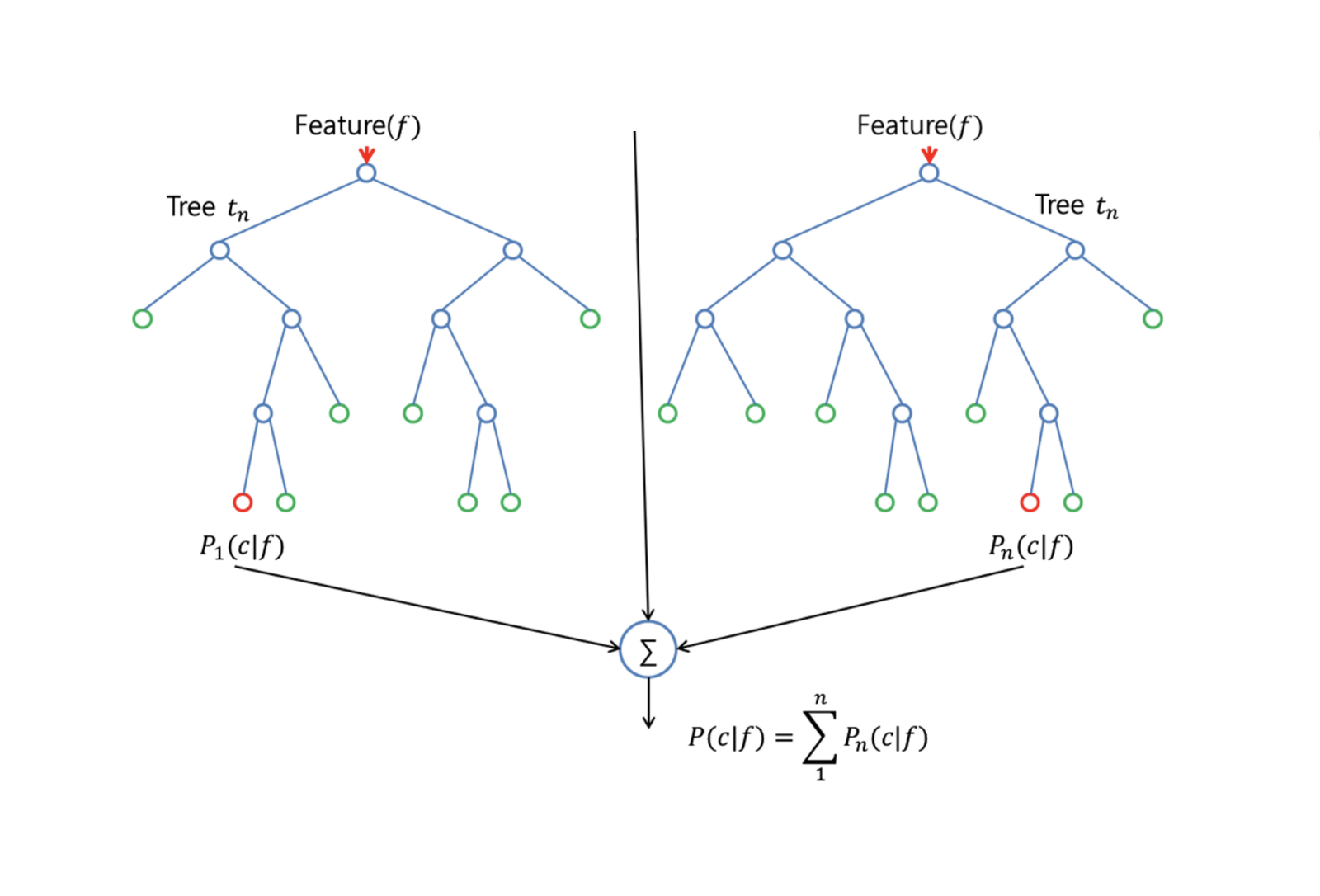
Pour faire croître une forêt aléatoire, vous devez :

• Supposez tout d'abord que le nombre de cas dans l'ensemble d'apprentissage est de K. Ensuite, prenez un échantillon aléatoire de ces K cas, puis utilisez cet échantillon comme ensemble d'apprentissage pour la croissance de l'arbre.

• S'il y a $p$ variables d'entrée, spécifiez un nombre $m < p$ tel qu'à chaque noeud, vous puissiez sélectionner $m$ variables aléatoires parmi les $p$. La meilleure division sur ces $m$ est utilisée pour diviser le nœud.

• Chaque arbre est ensuite cultivé de la manière la plus large possible et aucune taille n'est nécessaire.

• Enfin, les prédictions des arbres cibles sont agrégées pour prédire les nouvelles données.

Random Forests est très efficace pour estimer les données manquantes et maintenir la précision lorsqu'une grande partie des données est manquante. Il peut également équilibrer les erreurs dans les ensembles de données où les classes sont déséquilibrées. Plus important encore, il peut traiter des ensembles de données massifs avec une grande dimensionnalité. Cependant, l'un des inconvénients de l'utilisation des forêts aléatoires est que vous pouvez facilement suradapter des ensembles de données bruyants, en particulier dans le cas de la régression.

Renforcer l'efficacité

L'amplification est une autre approche permettant d'améliorer les prédictions résultant d'un arbre de décision. Comme le bagging et les forêts aléatoires, il s'agit d'une approche générale qui peut être appliquée à de nombreuses méthodes d'apprentissage statistique pour la régression ou la classification. Rappelons que le bagging consiste à créer plusieurs copies de l'ensemble de données d'apprentissage original à l'aide du bootstrap, à adapter un arbre de décision distinct à chaque copie, puis à combiner tous les arbres afin de créer un modèle prédictif unique. Notamment, chaque arbre est construit sur un ensemble de données bootstrap, indépendamment des autres arbres.

L'optimisation fonctionne de manière similaire, sauf que les arbres sont cultivés de manière séquentielle: chaque arbre est cultivé en utilisant les informations des arbres cultivés précédemment. Le boosting n'implique pas d'échantillonnage bootstrap ; au lieu de cela, chaque arbre est ajusté sur une version modifiée de l'ensemble de données d'origine.

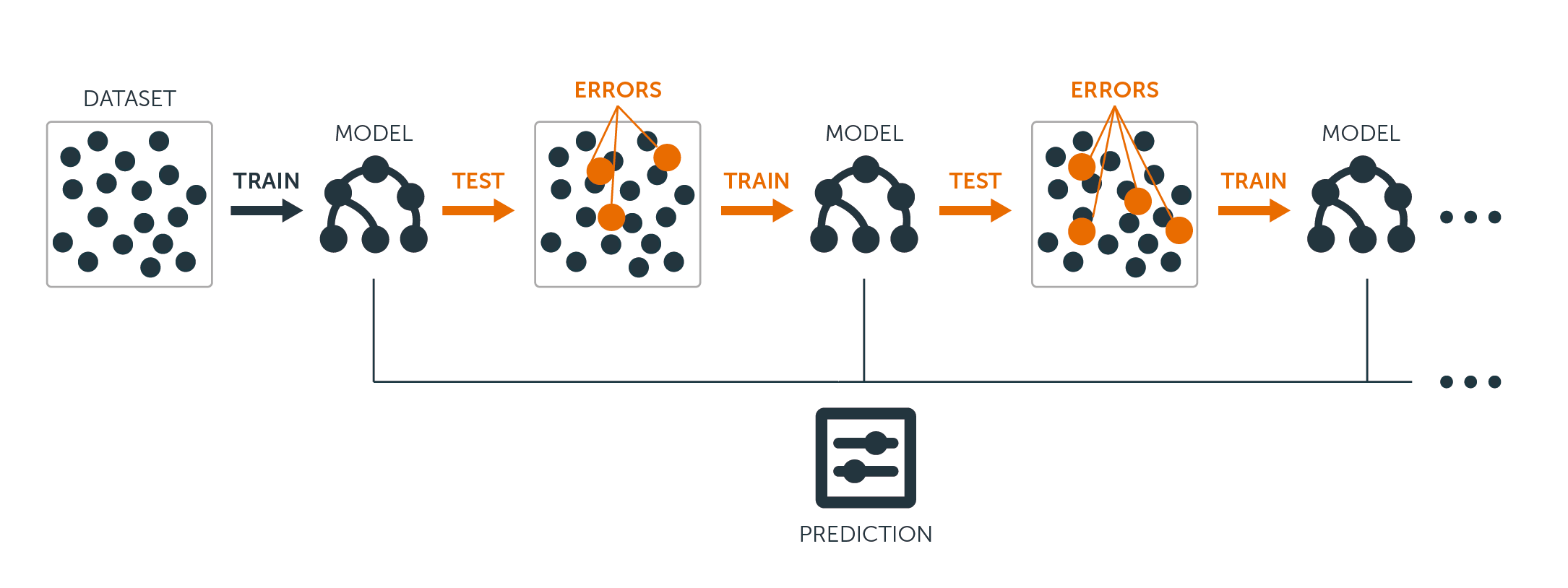
Pour les arbres de régression et de classification, le boosting fonctionne comme suit :

• Contrairement à l'adaptation d'un grand arbre de décision unique aux données, qui revient à adapter les données de manière stricte et potentiellement à les suradapter, l'approche boosting apprend lentement.

• Compte tenu du modèle actuel, vous adaptez un arbre de décision aux résidus du modèle. En d'autres termes, vous ajustez un arbre en utilisant les résidus actuels, plutôt que le résultat $Y$, comme réponse.

• Vous ajoutez ensuite ce nouvel arbre de décision à la fonction ajustée afin de mettre à jour les résidus. Chacun de ces arbres peut être assez petit, avec seulement quelques nœuds terminaux, déterminés par le paramètre $d$ dans l'algorithme. En ajustant de petits arbres aux résidus, vous améliorez lentement $hat{f}$ dans les domaines où il n'est pas performant.

• Le paramètre de rétrécissement $\nu$ ralentit encore le processus, ce qui permet à un plus grand nombre d'arbres de formes différentes d'attaquer les résidus.

Le boosting est très utile lorsque vous disposez d'un grand nombre de données et que vous vous attendez à ce que les arbres de décision soient très complexes. Le boosting a été utilisé pour résoudre de nombreux problèmes de classification et de régression, notamment l'analyse des risques, l'analyse des sentiments, la publicité prédictive, la modélisation des prix, l'estimation des ventes et le diagnostic des patients, entre autres.

Ces algorithmes combinent essentiellement les prédictions de plusieurs arbres de décision afin d'améliorer les performances globales et la stabilité. Après avoir compris les algorithmes avancés, nous allons, dans le cadre de ce tutoriel, nous intéresser aux modèles d'arbres de décision simples.

Construire des modèles d'arbres de décision étape par étape en R

Nous avons appris beaucoup de théorie et d'intuition sur les modèles d'arbres de décision et leurs variations, mais rien ne vaut la pratique et la construction de ces modèles, l'évaluation de leurs performances étape par étape.

Préparer les données pour la modélisation

Pour les exemples suivants, nous utiliserons le populaire ensemble de données sur le logement de Boston.

Le jeu de données Boston Housing contient des informations sur le marché du logement à Boston, Massachusetts, dans les années 1970. Il comporte 506 observations et 14 variables, dont 13 caractéristiques et 1 variable cible.

Les caractéristiques de l' ensemble de données sur le logement à Boston sont les suivantes :

• CRIM : Taux de criminalité par habitant par ville
• ZN : Proportion de terrains résidentiels zonés pour des lots de plus de 25 000 pieds carrés.
• INDUS : Proportion d'hectares consacrés à des activités autres que le commerce de détail par ville
• CHAS : Variable nominale "Charles River" (= 1 si le territoire est bordé par la rivière ; 0 sinon)
• NOX : Concentration de monoxyde d'azote (parties par 10 millions)
• RM : Nombre moyen de pièces par logement
• AGE : Proportion de logements occupés par leur propriétaire et construits avant 1940
• DIS : Distances pondérées par rapport à cinq centres d'emploi de Boston
• RAD : Indice d'accessibilité aux autoroutes radiales
• TAXE : Taux d'imposition sur la valeur totale de la propriété pour 10 000 dollars
• PTRATIO : Taux d'encadrement par ville
• Noirs : proportion de Noirs par ville
• LSTAT : Pourcentage de la population de statut inférieur

La variable cible est MEDV qui représente la valeur médiane des logements occupés par leurs propriétaires en milliers de dollars.

L'objectif est de prédire la valeur médiane des logements occupés par leurs propriétaires (en milliers de dollars) sur la base des caractéristiques données.

Dans R, les données sont fournies dans un paquetage appelé "MASS". Vous devrez installer plusieurs paquets pour ce tutoriel et les charger. Comme il s'agirait d'une répétition, nous allons démontrer ce processus avec le paquet MASS une fois, et vous le répéterez chaque fois que vous verrez un nouveau paquet utilisé dans ce guide.

# install the package
install.packages("MASS")

# Load the MASS package
library(MASS)

# Load the Boston Housing dataset
data(Boston)

Il est souvent nécessaire d'explorer les données à l'aide de visualisations et d'effectuer des étapes de prétraitement des données avant de passer à la modélisation. Examinons la distribution des variables à l'aide d'histogrammes.

Voici le code pour les créer :

# Load the library
library(tidymodels)
library(tidyr)

# Prepare the dataset for ggplot2
boston_data_long <- Boston %>%
 pivot_longer(cols = everything(),
              names_to = "variable",
              values_to = "value")

# Create a histogram for all numeric variables in one plot
boston_histograms <- ggplot(boston_data_long, aes(x = value)) +
 geom_histogram(bins = 30, color = "black", fill = "lightblue") +
 facet_wrap(~variable, scales = "free", ncol = 4) +
 labs(title = "Histograms of Numeric Variables in the Boston Housing Dataset",
      x = "Value",
      y = "Frequency") +
 theme_minimal()

# Plot the histograms
print(boston_histograms)

Le résultat ressemble à ceci :

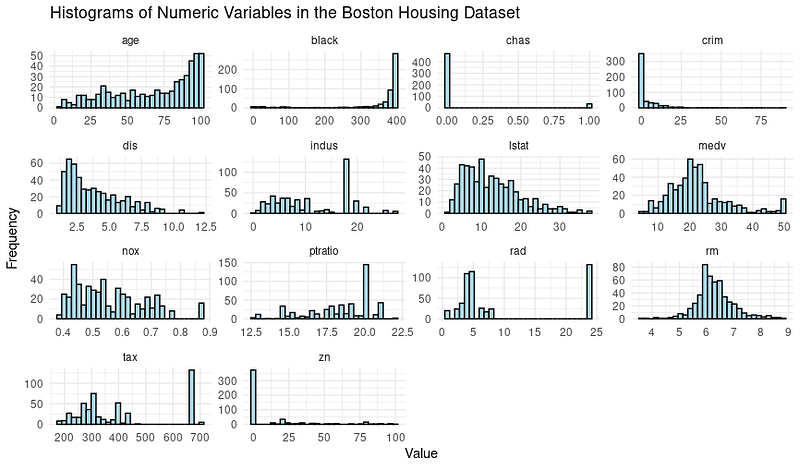
Nous remarquons quelques valeurs aberrantes, en particulier dans les colonnes telles que RAD, TAX et NOX. Notre objectif pour ce tutoriel est de nous concentrer sur la phase de modélisation de l'arbre de décision ; nous allons donc diviser l'ensemble de données en ensembles de formation et de test.

# Split the data into training and testing sets

set.seed(123)
data_split <- initial_split(Boston, prop = 0.75)
train_data <- training(data_split)
test_data <- testing(data_split)

Passons maintenant à la modélisation et à l'évaluation des performances du modèle.

Modélisation par arbre de décision simple

En utilisant la fonction decision_tree() du package Tidymodels de R, il est facile de créer une spécification de modèle d'arbre de décision, puis d'ajuster le modèle sur les données d'apprentissage.

# Create a decision tree model specification
tree_spec <- decision_tree() %>%
 set_engine("rpart") %>%
 set_mode("regression")

# Fit the model to the training data
tree_fit <- tree_spec %>%
 fit(medv ~ ., data = train_data)

Nous utilisons ici le modèle de "régression", et pour un arbre de décision de classification, nous devrions utiliser le mode de "classification".

Évaluation de la performance de la modélisation de l'arbre décisionnel

Pour évaluer les performances du modèle, nous utiliserons le progiciel Tidymodels pour calculer l'erreur quadratique moyenne (RMSE) et la valeur R-carré de notre modèle d'arbre de décision sur les données de test.

# Make predictions on the testing data
predictions <- tree_fit %>%
 predict(test_data) %>%
 pull(.pred)

# Calculate RMSE and R-squared
metrics <- metric_set(rmse, rsq)
model_performance <- test_data %>%
 mutate(predictions = predictions) %>%
 metrics(truth = medv, estimate = predictions)

print(model_performance)

Vous obtiendrez un résultat présentant deux mesures de performance : Erreur quadratique moyenne (RMSE) et R².

 .metric .estimator .estimate
 <chr>   <chr>          <dbl>
1 rmse    standard       5.22
2 rsq     standard       0.689

Analyse des résultats du modèle

Les résultats de notre modèle sont-ils donc suffisants ?

• RMSE (erreur quadratique moyenne) : Elle mesure la différence moyenne entre les valeurs prédites et les valeurs réelles. Dans votre cas, le RMSE est de 5,22, ce qui signifie qu'en moyenne, les prédictions faites par le modèle d'arbre de décision s'écartent d'environ 5,22 unités des valeurs réelles. Une valeur RMSE plus faible est généralement préférable, car elle indique des erreurs de prédiction moins importantes.
• R-carré (R²) : Cette mesure permet de déterminer dans quelle mesure le modèle explique la variance de la variable cible. Il est compris entre 0 et 1, une valeur plus élevée indiquant une meilleure adéquation. Dans votre cas, le R² est de 0,689, ce qui signifie que le modèle explique environ 68,9 % de la variance de la variable cible (MEDV).

Nous pouvons également optimiser les hyperparamètres pour améliorer les performances ou opter pour des modèles plus complexes tels que Random Forests et XGBoost, au détriment de l'interprétabilité du modèle.

Prédiction des résultats à l'aide du modèle de l'arbre de décision

Une fois que vous êtes satisfait du modèle, il est temps de le laisser faire des prédictions.

Nous procédons de la même manière que pour les données de test à l'aide de la fonction predict(), mais nous devons fournir un nouvel ensemble de données imitant les informations relatives à une nouvelle maison à Boston. Il s'agit d'un scénario possible lorsque le modèle est mis en service dans un environnement de production.

# Make predictions on new data
new_data <- tribble(
 ~crim, ~zn, ~indus, ~chas, ~nox, ~rm, ~age, ~dis, ~rad, ~tax, ~ptratio, ~black, ~lstat,
 0.03237, 0, 2.18, 0, 0.458, 6.998, 45.8, 6.0622, 3, 222, 18.7, 394.63, 2.94
)
predictions <- predict(tree_fit, new_data)
print(predictions)

Vous obtiendrez ainsi la valeur moyenne prévue (en milliers de dollars) de cette maison :

# A tibble: 1 × 1
 .pred
 <dbl>
1  37.8

Maintenant que vous connaissez les étapes de la construction d'un modèle d'arbre décisionnel, nous allons nous concentrer sur la façon dont nous pouvons interpréter ce qui se passe à l'intérieur du modèle pour nous-mêmes et pour les parties prenantes qui utilisent la solution que nous venons de construire.

Interprétation de l'arbre de décision

L'avantage le plus important, comme nous l'avons indiqué précédemment, est l'interprétabilité des modèles d'arbres de décision. Visualisons l'arbre de décision pour mieux comprendre le modèle :

# Load the library
library(rpart.plot)

# Plot the decision tree
rpart.plot(tree_fit$fit, type = 4, extra = 101, under = TRUE, cex = 0.8, box.palette = "auto")

Vous obtiendrez un graphique comme celui-ci :

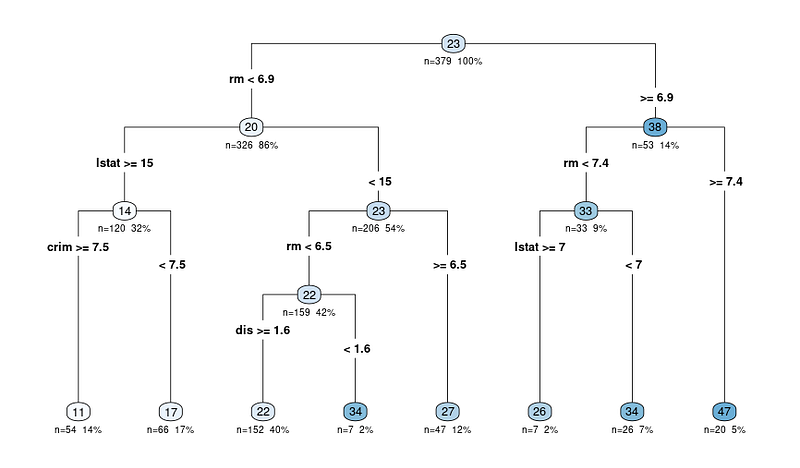
Le diagramme de sortie de la fonction rpart.plot montre une représentation du modèle sous forme d'arbre de décision. Dans ce diagramme, chaque nœud représente une division de l'arbre de décision en fonction des variables prédictives. Le diagramme de sortie comprend plusieurs informations qui peuvent nous aider à interpréter l'arbre de décision :

Les diagrammes en arbre commencent par le nœud

Les nœuds sont représentés par des cercles et sont reliés par des lignes, ce qui montre la structure hiérarchique de l'arbre de décision. L'arbre commence par un nœud racine au sommet et se ramifie en nœuds internes, pour aboutir finalement aux nœuds terminaux ou feuilles au bas de l'arbre.

Les critères de fractionnement pour chaque nœud interne

Chaque nœud interne affiche le critère de division, qui est la variable prédictive et la valeur utilisée pour diviser les données en deux sous-ensembles.

Par exemple, un nœud peut indiquer "RM < 6.8", ce qui signifie que les observations dont le nombre moyen de pièces par logement (RM) est inférieur à 6,8 suivront la branche de gauche, tandis que les observations dont le RM est supérieur ou égal à 6,8 suivront la branche de droite.

N : Nombre d'observations après le fractionnement

La valeur n de chaque nœud représente le nombre d'observations de l'ensemble de données qui entrent dans ce nœud particulier. Par exemple, si un nœud indique "n = 100", cela signifie que 100 observations de l'ensemble de données répondent aux critères des nœuds parents de ce nœud.

X% : La proportion des observations totales de l'ensemble des données qui ont atteint le nœud en question.

La valeur en pourcentage vous aide à comprendre la taille relative de chaque nœud par rapport à l'ensemble des données, en montrant comment les données sont divisées et distribuées dans l'arbre. Un pourcentage élevé signifie qu'une plus grande proportion des données a suivi le chemin de décision menant au nœud spécifique, tandis qu'un pourcentage plus faible indique une plus petite proportion des données atteignant ce nœud.

Valeur prédite pour chaque nœud

La valeur prédite à chaque nœud est affichée sous la forme d'un nombre dans un cercle coloré (nœud). Dans un arbre de régression, il s'agit de la valeur moyenne de la variable cible pour toutes les observations qui se trouvent dans ce nœud.

Par exemple, le dernier nœud principal affichant 47 signifie que la valeur moyenne de la variable cible (dans notre cas, la valeur médiane des logements occupés par leur propriétaire) pour toutes les observations dans ce nœud est de 47.

Commencez par le nœud racine et suivez les branches

Ainsi, lorsque vous interprétez des résultats, vous commencez par le nœud racine et vous suivez les branches en fonction des critères de division jusqu'à ce que vous atteigniez un nœud terminal. La valeur prédite dans le nœud terminal donne la prédiction du modèle pour une observation donnée et la justification de la décision.

Extraction des règles de l'arbre de décision

Si vous préférez toujours extraire les règles sous forme de texte (au lieu de parcourir le diagramme), vous pouvez également le faire en utilisant la même bibliothèque que celle utilisée pour tracer le diagramme.

Voici le code pour le faire :

rules <- rpart.rules(tree_fit$fit)
print(rules)

Vous obtiendrez une sortie avec les valeurs prédites et les règles suivies pour arriver à cette valeur, comme ci-dessous :

medv                                                              
  11 when rm <  6.9        & lstat >= 15 & crim >= 7.5            
  17 when rm <  6.9        & lstat >= 15 & crim <  7.5            
  22 when rm <  6.5        & lstat <  15               & dis >= 1.6
  26 when rm is 6.9 to 7.4 & lstat >=  7                          
  27 when rm is 6.5 to 6.9 & lstat <  15                          
  34 when rm <  6.5        & lstat <  15               & dis <  1.6
  34 when rm is 6.9 to 7.4 & lstat <   7                          
  47 when rm >=        7.4

Maintenant que vous voyez les règles, vous vous demandez peut-être comment la décision peut être prise avec 3-4 variables lorsque nous introduisons beaucoup plus de variables dans l'arbre de décision.

Il s'avère que certaines variables sont plus importantes que d'autres. Comprenons mieux ce concept.

Comprendre les variables importantes des arbres de décision

Nous avons déjà découvert le diagramme en arbre et le fonctionnement du modèle. Un dernier aspect de l'interprétation consiste à comprendre les variables importantes de l'ensemble de données.

Voici pourquoi c'est crucial :

• Sélection des caractéristiques. L'identification des variables importantes peut vous aider à vous concentrer sur les caractéristiques pertinentes et éventuellement à supprimer celles qui sont moins importantes, ce qui simplifie votre modèle et réduit le bruit.
• Connaissance du domaine. Le fait de savoir quelles sont les caractéristiques les plus importantes peut vous aider à mieux comprendre les relations entre les variables et la variable cible dans le contexte de votre problème spécifique.
• Modèle d'interprétation. La compréhension des caractéristiques clés qui déterminent les prédictions du modèle peut fournir des informations précieuses pour le processus de prise de décision.

Dans les arbres de décision, l'importance des variables est généralement déterminée par les caractéristiques utilisées pour la division des nœuds. Les caractéristiques utilisées pour le fractionnement plus haut dans l'arbre ou utilisées plus fréquemment peuvent être considérées comme plus importantes.

L'importance d'une variable peut être quantifiée par la réduction de la mesure d'impureté (par exemple, l'indice de Gini ou l'erreur quadratique moyenne) qu'elle apporte lorsqu'elle est utilisée pour le fractionnement. Le paquet "VIP" de R a éliminé toutes les complexités, et le tracé peut être obtenu grâce au code ci-dessous :

# Load the necessary library
library(vip)

# Create a variable importance plot
var_importance <- vip::vip(tree_fit, num_features = 10)
print(var_importance)

Vous obtiendrez le graphique d'importance variable ci-dessous :

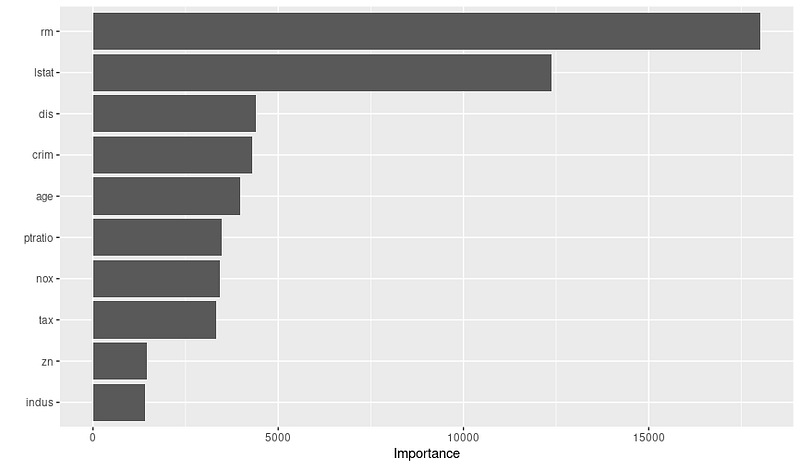
Une fois que vous aurez vu le graphique, vous pourrez faire des recherches plus approfondies sur les raisons pour lesquelles ces variables sont importantes, en collaborant avec des experts du domaine. Par exemple, sur la base du graphique ci-dessus, nous pouvons déduire les 3 variables les plus importantes et leur raison d'être :

1. RM : Le nombre moyen de pièces par logement est une caractéristique très importante, suggérant que les maisons avec plus de pièces ont tendance à avoir des valeurs médianes plus élevées.
2. LSTAT : Le pourcentage de la population ayant un statut socio-économique inférieur est une autre variable significative, indiquant que les quartiers ayant un statut inférieur sont susceptibles d'avoir une valeur médiane du logement plus faible.
3. DIS : La distance pondérée par rapport aux centres d'emploi est une variable essentielle, qui montre que les maisons situées à proximité de grands centres d'emploi sont susceptibles d'avoir une valeur médiane plus élevée.

N'oubliez donc pas de vérifier le graphique d'importance des variables avant de finaliser votre modèle ; cela peut vous aider à créer et à sélectionner de meilleures caractéristiques afin d'optimiser les performances.

Conclusion

Dans ce tutoriel, nous avons exploré les concepts fondamentaux des arbres de décision et abordé non seulement la construction de modèles mais aussi leur interprétation. Les arbres de décision sont des modèles puissants et interprétables pour les tâches de classification et de régression, ce qui en fait un outil essentiel dans l'arsenal d'un scientifique des données.

Au fur et à mesure que vous développez vos compétences, nous vous encourageons à plonger plus profondément dans le monde des arbres de décision, à explorer d'autres algorithmes et à améliorer vos capacités de programmation R. Voici quelques ressources pour votre prochaine étape :

• Fondamentaux de l'apprentissage automatique en R
• Introduction au Feature Engineering en R
• Modélisation avec Tidymodels dans R
• Apprentissage automatique avec des modèles arborescents en R

Il ne fait aucun doute que l'élargissement de vos connaissances et l'expérimentation de nouveaux outils et techniques vous permettront de relever divers défis et d'apporter une contribution précieuse à vos projets.