programa
Imagina que estás explorando un vasto sistema de cuevas. Elige un túnel y síguelo hasta donde llegue, cada vez más profundo, hasta que llegues a un callejón sin salida. Luego, retrocede hasta el último cruce e intenta un nuevo túnel. Este método de exploración profunda, volviendo sobre tus pasos sólo cuando es necesario, se parece mucho a la búsqueda en profundidad (DFS), un algoritmo fundamental para navegar por estructuras de datos como grafos y árboles.
Si lo tuyo son las estructuras de datos, los algoritmos y la resolución de problemas, DataCamp te tiene cubierto: Aprende más sobre las diferentes estructuras de datos y los mejores algoritmos para explorarlas en el curso Estructuras de Datos y Algoritmos en Python y en nuestro Estructuras de Datos: Una guía completa con ejemplos de Python tutorial.
¿Qué es la búsqueda en profundidad?
La búsqueda en profundidad (DFS) es un algoritmo utilizado para recorrer o buscar en una estructura de datos, como un grafo o un árbol. La idea fundamental de DFS es que explora una rama del grafo o árbol lo más abajo posible antes de retroceder para explorar ramas alternativas. Este enfoque contrasta con la búsqueda de amplitud primero, que explora todos los nodos del nivel de profundidad actual antes de pasar al siguiente. Puedes leer más sobre la búsqueda amplia AQUÍ.
Piensa en la búsqueda en profundidad como una forma de explorar un laberinto: eliges un camino y lo sigues hasta que llegas a un callejón sin salida. Una vez que llegues al final de ese camino, retrocede hasta el último punto de decisión e intenta una ruta diferente. Esta exploración profunda hace que el DFS sea una opción excelente cuando el objetivo es explorar a fondo una estructura, especialmente una con muchos caminos potenciales.

La DFS es especialmente útil en problemas en los que necesitas explorar todas las soluciones posibles.
Algunos ejemplos son:
- Navegar por árboles de decisión en IA, donde cada rama representa una secuencia de elecciones, y el objetivo es evaluar todos los resultados posibles.
- Problemas de búsqueda de rutas, como navegar por un tablero de juego o encontrar rutas en un mapa, que requieren búsquedas exhaustivas.
DFS garantiza que cada nodo se visite una vez y que el algoritmo cubra todo el grafo o árbol.
Características principales de la búsqueda en profundidad en Python
La búsqueda en profundidad tiene un enfoque sistemático para explorar nodos y retroceder sólo cuando es necesario. Veamos algunas de sus características principales.
Naturaleza recursiva
En esencia, DFS funciona recursivamente, lo que significa que resuelve el problema llamándose a sí mismo repetidamente a medida que explora más profundamente la estructura. Cuando DFS se sumerge en una rama, la explora lo más profundamente posible antes de volver a explorar otras ramas. Este proceso de profundizar en un camino y retroceder cuando no hay más opciones se gestiona idealmente mediante la recursividad. Consulta Comprender las funciones recursivas en Python para ver en profundidad qué son las funciones recursivas y cuándo son útiles.
Retroceder
El retroceso es esencial para la DFS. Cuando el algoritmo llega a un nodo que no tiene vecinos no visitados, vuelve sobre sus pasos hasta el nodo anterior y comprueba si allí existen otros vecinos no visitados. Si las hay, las explorará; si no, sigue retrocediendo. Este ciclo de profundizar y retroceder continúa hasta que se han cubierto todos los caminos posibles o se ha cumplido una condición de salida.
Ciclos de manipulación
Los grafos pueden contener ciclos, que son caminos que vuelven sobre sí mismos. Sin las precauciones adecuadas, el DFS podría volver a visitar infinitamente los nodos en estos ciclos. Al marcar cada nodo como visitado la primera vez que se encuentra, DFS puede evitar volver sobre sus pasos innecesariamente. De este modo, incluso en grafos cíclicos, DFS sigue siendo eficaz y evita los bucles infinitos.
Exploración exhaustiva
Uno de los rasgos distintivos del DFS es su capacidad para explorar completamente una estructura. El algoritmo continúa hasta que se hayan visitado todos los nodos. Esto es especialmente útil cuando necesitas asegurarte de que no se pasa por alto ninguna solución potencial, como al resolver puzzles, explorar árboles de decisión o recorrer laberintos.
Implementar la búsqueda en profundidad en Python
Hay dos formas principales de implementar una búsqueda en profundidad en Python: recursivamente e iterativamente. Cada enfoque tiene sus ventajas y sus inconvenientes, y la elección depende a menudo del tamaño del gráfico y del problema que estés resolviendo.
Para ilustrar ambos métodos, creemos un árbol de decisión sencillo y utilicemos DFS para recorrerlo. Utilizaremos Python para nuestro ejemplo. Siempre puedes consultar la pista de habilidades de Programación en Python para refrescar tus conocimientos de Python.
Tomemos como ejemplo un árbol de decisión binario. Aquí tienes una estructura de árbol sencilla en la que cada nodo tiene dos ramas hijas:
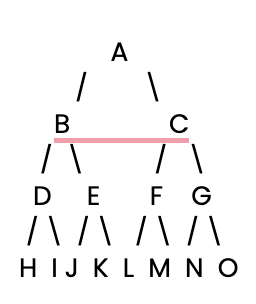
Definamos este árbol de decisión explícitamente en Python como un diccionario.
# Define the decision tree as a dictionary
tree = {
'A': ['B', 'C'],
'B': ['D', 'E'],
'C': ['F', 'G'],
'D': ['H', 'I'],
'E': ['J', 'K'],
'F': ['L', 'M'],
'G': ['N', 'O'],
'H': [], 'I': [], 'J': [], 'K': [],
'L': [], 'M': [], 'N': [], 'O': []
}DFS recursivo
El DFS suele implementarse de forma recursiva. En cada nodo, DFS se llama a sí mismo en sus nodos hijos hasta que no haya más que visitar, y entonces retrocede. Aquí tienes una función DFS recursiva para recorrer el árbol.
# Recursive DFS function
def dfs_recursive(tree, node, visited=None):
if visited is None:
visited = set() # Initialize the visited set
visited.add(node) # Mark the node as visited
print(node) # Print the current node (for illustration)
for child in tree[node]: # Recursively visit children
if child not in visited:
dfs_recursive(tree, child, visited)
# Run DFS starting from node 'A'
dfs_recursive(tree, 'A')En esta versión recursiva, empezamos en el nodo raíz A y exploramos cada rama antes de retroceder para explorar las alternativas. Si ejecutamos este código, mostrará el camino que ha seguido al explorar este árbol:
A
B
D
H
I
E
J
K
C
F
L
M
G
N
ODFS iterativa
Para árboles de decisión muy grandes, el límite de profundidad de recursión de Python podría causar problemas. En ese caso, podemos implementar DFS de forma iterativa, utilizando una pila para gestionar los nodos que hay que visitar. He aquí cómo podríamos aplicar la DFS iterativa para el mismo árbol de decisión:
# Iterative DFS function
def dfs_iterative(tree, start):
visited = set() # Track visited nodes
stack = [start] # Stack for DFS
while stack: # Continue until stack is empty
node = stack.pop() # Pop a node from the stack
if node not in visited:
visited.add(node) # Mark node as visited
print(node) # Print the current node (for illustration)
stack.extend(reversed(tree[node])) # Add child nodes to stack
# Run DFS starting from node 'A'
dfs_iterative(tree, 'A')Este enfoque iterativo evita los límites de profundidad de la recursión manejando manualmente la pila, lo que puede ser útil para árboles grandes o estructuras profundas. Al ejecutar este código se obtiene el mismo resultado que antes.
Cuándo utilizar DFS Recursivo Versus Iterativo
Tanto los enfoques recursivos como los iterativos de la búsqueda en profundidad son herramientas valiosas, pero la elección entre ellos depende de la estructura del grafo y de tus necesidades específicas. Veamos más de cerca los puntos fuertes y las limitaciones de cada enfoque.
DFS recursivo
En general, prefiero la sencillez y la elegancia del DFS recursivo. Este enfoque es intuitivo y limpio.
Pros:
- Simplicidad: El código es compacto y refleja bien el problema.
- Legibilidad: Más fácil de entender, sobre todo para problemas pequeños o medianos.
Contras:
- Límite de profundidad de recursión: Para grafos grandes, podrías llegar al límite de profundidad de recursión de Python.
La recursión es ideal para problemas en los que el árbol o grafo es relativamente pequeño y cabe cómodamente dentro de la profundidad de recursión de Python.
DFS iterativa
Aunque es ligeramente más complejo de escribir, el DFS iterativo es más flexible y puede manejar problemas mayores sin preocuparse por los límites de recursividad. En lugar de confiar en la pila de llamadas de Python, el DFS iterativo gestiona explícitamente los nodos a explorar mediante una pila.
Pros:
- Sin límite de recursión: Gestionar la pila manualmente evita el límite de profundidad de recursión de Python.
Contras:
- Más Código: El DFS iterativo requiere más configuración y puede ser menos intuitivo.
- Legibilidad: El código suele ser algo más verboso, lo que hace que sea más difícil de seguir.
El enfoque iterativo es mejor para problemas grandes o complejos en los que la profundidad de la recursión es un problema. También es útil cuando necesitas más control sobre el recorrido.
Complejidad temporal y espacial
DFS es un algoritmo eficiente, pero su rendimiento se ve influido por el tamaño y la estructura del grafo que está explorando. El tiempo que DFS tarda en ejecutarse y la cantidad de memoria que utiliza depende del número de nodos que visita, así como de las conexiones entre ellos.
Utilizamos la notación BigO para hablar de complejidad. Para refrescar conocimientos sobre la notación Big O, consulta Notación Big O y Guía de Complejidad Temporal: Intuición y Matemáticas.
Complejidad temporal
La complejidad temporal del DFS se define como O(V + E), donde V es el número de nodos y E es el número de conexiones (llamadas "aristas"). DFS visita cada nodo y cada conexión una vez. Por tanto, el tiempo total que tarda el DFS depende de cuántos nodos y conexiones haya.
Complejidad espacial
El espacio utilizado en DFS depende de cuántos nodos esté controlando el algoritmo en cada momento. Tanto el DFS recursivo como el iterativo utilizan una pila para llevar la cuenta de los nodos que se exploran. En el peor de los casos, la memoria utilizada puede contener todos los nodos del grafo, lo que conlleva una complejidad espacial de O(V).
Explora otras formas de medir la complejidad de los algoritmos en el tutorial Analizar la complejidad del código mediante Python.
Aplicaciones reales de la búsqueda en profundidad primero
El DFS es útil en muchos campos, como la informática, la IA y el desarrollo de juegos. Consulta la tabla siguiente para ver algunas aplicaciones habituales del DFS.
| Aplicación | Descripción |
|---|---|
| Resolución de laberintos | DFS explora caminos en un laberinto sumergiéndote en un camino hasta llegar a un callejón sin salida, y luego retrocede para explorar otras rutas. Garantiza encontrar un camino, aunque no necesariamente el más corto. |
| Resolver puzzles | Muchos rompecabezas, como el Sudoku o el problema N-Queens, requieren que el DFS explore posibles soluciones y retroceda cuando una configuración no funciona. |
| Pathfinding en los juegos | El DFS ayuda a la IA en los juegos de estrategia a explorar secuencias profundas de movimientos, simulando los resultados para fundamentar las decisiones. |
| Detección del ciclo | DFS detecta ciclos comprobando si vuelve a visitar algún nodo mientras explora rutas en grafos, útil en tareas como la resolución de dependencias. |
| Ordenación topológica | Utilizado en grafos acíclicos dirigidos, el DFS ordena los nodos en función de las dependencias, como en la programación de proyectos, donde el orden de las tareas es importante. |
Búsqueda en profundidad Vs. Otros algoritmos de búsqueda
Comparemos el DFS con otros algoritmos bien conocidos, como la búsqueda amplitud-primera, el Algoritmo de Dijkstra y A*.
Búsqueda en profundidad frente a búsqueda en amplitud
La búsqueda en profundidad (BFS) explora un grafo nivel a nivel, visitando todos los nodos de la profundidad actual antes de pasar a la siguiente. El BFS es especialmente útil cuando el objetivo es encontrar el camino más corto en un grafo no ponderado. Sin embargo, el BFS puede utilizar mucha memoria, sobre todo en grafos anchos, porque debe llevar la cuenta de todos los nodos de cada nivel. BFS es una opción excelente para el análisis de redes sociales o problemas sencillos de encaminamiento.
En cambio, la búsqueda en profundidad es útil cuando el objetivo es explorar todos los caminos o soluciones posibles, como la resolución de puzzles o la búsqueda de ciclos en un grafo. A diferencia del BFS, el DFS no garantiza el camino más corto. Pero es más eficiente en cuanto a memoria, ya que sólo guarda la ruta actual.
Puedes obtener más información sobre la búsqueda exhaustiva Búsqueda exhaustiva: Guía para principiantes con ejemplos de Python.
DFS frente al algoritmo de Dijkstra
El algoritmo de Dijkstra está diseñado para encontrar el camino más corto en grafos con aristas ponderadas, donde cada enlace entre nodos tiene un coste asociado. El de Dijkstra funciona explorando siempre primero el camino de menor coste, lo que garantiza que se encuentre el camino óptimo desde el nodo inicial a cualquier otro nodo. Sin embargo, puede ser más lento que DFS en determinadas exploraciones de grafos sencillos. El de Dijkstra es perfecto para tareas en las que importan los pesos de los bordes, como las redes de carreteras o los problemas de encaminamiento más complejos.
La búsqueda en profundidad no tiene en cuenta los pesos de las aristas, por lo que no garantiza el camino óptimo. Sin embargo, es más rápido que el de Dijkstra en grafos no ponderados o cuando los pesos de las aristas son irrelevantes.
Puedes obtener más información sobre el Algoritmo de Dijkstra en Implementación del Algoritmo de Dijkstra en Python: Un tutorial paso a paso.
DFS frente a A*
A* (pronunciado "A-estrella") es un algoritmo que mejora el de Dijkstra incorporando una heurística para guiar su búsqueda. Esto lo hace más rápido y eficaz en muchos casos. A* se equilibra entre explorar los caminos de menor coste (como el de Dijkstra) y dirigirse directamente a la meta, utilizando una heurística como la distancia en línea recta a la meta. Esto hace que A* sea muy eficaz para tareas como la navegación GPS o la búsqueda de trayectorias en videojuegos.
La búsqueda en profundidad no utiliza ninguna heurística, lo que significa que carece de la "dirección" que utiliza A* para alcanzar eficazmente el objetivo. DFS es más adecuado para problemas que requieren una búsqueda exhaustiva de todo el grafo o árbol de decisión, mientras que A* es mejor cuando hay que encontrar el camino más corto de forma eficiente con ayuda de una heurística.
Puedes obtener más información sobre A* en Wikipedia.
Errores comunes y cómo evitarlos
Al utilizar la búsqueda en profundidad, pueden surgir varios problemas comunes, sobre todo con grafos grandes.
No rastrea los nodos visitados
Surge un problema cuando se olvida hacer un seguimiento de los nodos que ya han sido visitados. Esto puede dar lugar a bucles infinitos, especialmente en grafos que contienen ciclos. Cuando DFS vuelve a visitar nodos sin comprobar si han sido explorados, puede quedarse atascado en un bucle infinito. Para evitarlo, asegúrate de mantener una lista de los nodos visitados. Antes de visitar un nuevo nodo, comprueba si ya está en el conjunto visitado. Si lo es, puedes saltártelo con seguridad y evitar quedar atrapado.
Desbordamiento de pila en DFS recursivo
En Python, la profundidad de recursión está limitada a unos 1.000 niveles por defecto, lo que significa que las llamadas recursivas anidadas profundamente en grafos grandes pueden provocar un RecursionError. Para evitarlo, podemos utilizar una implementación DFS iterativa para grafos grandes. Al mantener esta pila como una lista, evitamos los límites de profundidad de recursión y podemos manejar con seguridad grafos mucho mayores.
Confundir una solución con el camino más corto
También es importante recordar que DFS no garantiza el camino más corto entre dos nodos. Como DFS sigue un camino en profundidad antes de retroceder para explorar otros, puede encontrar una solución, pero puede que no sea la más directa.
Conclusión
La búsqueda en profundidad es un potente algoritmo para explorar y recorrer grafos y árboles. Con su capacidad para profundizar en los caminos y explorar todas las posibilidades, es muy adecuado para una gran variedad de problemas como la resolución de laberintos, rompecabezas y exploración de árboles de decisión.
Si te interesan los algoritmos de búsqueda, consulta mis otros artículos de esta serie: Búsqueda binaria en Python: Una guía completa para una búsqueda eficiente y Búsqueda Amplia-Primera: Guía para principiantes con ejemplos de Python. También te puede interesar Árbol AVL: Guía Completa Con Implementación En Python, e Introducción al Análisis de Redes en Python.

Soy doctor con 13 años de experiencia trabajando con datos en un entorno de investigación biológica. Creo software en varios lenguajes de programación, como Python, MATLAB y R. Me apasiona compartir mi amor por el aprendizaje con el mundo.
Preguntas frecuentes sobre la búsqueda en profundidad en Python
¿Qué es la búsqueda en profundidad?
La búsqueda en profundidad es un algoritmo utilizado para explorar estructuras de datos en forma de árbol o grafo. Su estrategia prioriza explorar una rama lo más profundamente posible antes de retroceder para investigar ramas alternativas.
¿En qué se diferencia la búsqueda en profundidad de la búsqueda en amplitud?
DFS profundiza en una rama antes de retroceder, mientras que BFS explora todos los nodos vecinos en el nivel actual antes de pasar al siguiente nivel.
¿Cuáles son algunas ventajas del DFS?
DFS es una forma eficiente en memoria de explorar un grafo o árbol de forma exhaustiva.
¿Cuáles son algunas desventajas del DFS?
No se garantiza que DFS encuentre el camino más corto y no tiene en cuenta los pesos del grafo.
¿Cuáles son algunas aplicaciones del DFS en el mundo real?
El DFS puede aplicarse a la resolución de laberintos y rompecabezas, a la búsqueda de caminos y al rastreo web.