Lernpfad
Stell dir vor, du erkundest ein riesiges Höhlensystem. Du wählst einen Tunnel aus und folgst ihm so weit wie möglich, immer tiefer und tiefer, bis du auf eine Sackgasse stößt. Dann fährst du zurück zur letzten Kreuzung und versuchst einen neuen Tunnel. Diese Methode der Tiefenerkundung, bei der du deine Schritte nur dann zurückverfolgst, wenn es nötig ist, ähnelt der Deep-First-Suche (DFS), einem grundlegenden Algorithmus zur Navigation in Datenstrukturen wie Graphen und Bäumen.
Wenn du dich für Datenstrukturen, Algorithmen und Problemlösungen interessierst, bist du beim DataCamp genau richtig: Erfahre mehr über verschiedene Datenstrukturen und die besten Algorithmen, mit denen du sie erkunden kannst, im Kurs Datenstrukturen und Algorithmen in Python und in unserem Datenstrukturen: Ein umfassendes Handbuch mit Python-Beispielen tutorial.
Was ist Depth-First Search?
Die Tiefensuche (Depth-first search, DFS) ist ein Algorithmus, der verwendet wird, um eine Datenstruktur, wie z. B. einen Graphen oder einen Baum, zu durchlaufen oder zu durchsuchen. Die Grundidee des DFS ist, dass es einen Zweig des Graphen oder Baums so weit wie möglich erkundet, bevor es zurückgeht, um alternative Zweige zu erkunden. Dieser Ansatz steht im Gegensatz zur Breadth-First-Suche, bei der alle Knoten auf der aktuellen Tiefenstufe untersucht werden, bevor die nächste Stufe erreicht wird. Du kannst HIER über die Breadth-First-Suche lesen.
Stell dir die Deep-First-Suche wie die Erkundung eines Labyrinths vor: Du wählst einen Weg und folgst ihm, bis du in eine Sackgasse gerätst. Sobald du das Ende des Weges erreicht hast, gehst du zum letzten Entscheidungspunkt zurück und versuchst eine andere Route. Diese tiefe Erkundung macht die DFS zu einer ausgezeichneten Wahl, wenn es darum geht, eine Struktur vollständig zu erkunden, insbesondere eine mit vielen potenziellen Pfaden.

Die DFS ist besonders nützlich bei Problemen, bei denen du alle möglichen Lösungen untersuchen musst.
Hier ein paar Beispiele:
- Die Navigation in Entscheidungsbäumen in der KI, bei der jeder Zweig eine Folge von Entscheidungen darstellt und das Ziel darin besteht, alle möglichen Ergebnisse zu bewerten.
- Wegfindungsprobleme, wie das Navigieren auf einem Spielbrett oder das Finden von Routen auf einer Karte, die eine umfassende Suche erfordern.
DFS stellt sicher, dass jeder Knoten einmal besucht wird und dass der Algorithmus den gesamten Graphen oder Baum abdeckt.
Hauptmerkmale der Depth-First-Suche in Python
Bei der Depth-First-Suche werden die Knoten systematisch erkundet und nur bei Bedarf ein Backtracking durchgeführt. Werfen wir einen Blick auf einige seiner wichtigsten Eigenschaften.
Rekursive Natur
Im Kern arbeitet die DFS rekursiv, das heißt, sie löst das Problem, indem sie sich selbst wiederholt aufruft, während sie tiefer in die Struktur vordringt. Wenn die DFS in einen Zweig eintaucht, erforscht sie ihn so tief wie möglich, bevor sie wieder hochkommt, um andere Zweige zu erforschen. Dieser Prozess, bei dem du tiefer in einen Pfad eindringst und zurückgehst, wenn es keine weiteren Optionen gibt, wird idealerweise durch Rekursion gehandhabt. In Rekursive Funktionen in Python verstehen erfährst du, was rekursive Funktionen sind und wann sie nützlich sind.
Backtracking
Backtracking ist für die DFS unerlässlich. Wenn der Algorithmus einen Knoten erreicht, der keine unbesuchten Nachbarn hat, geht er seine Schritte zum vorherigen Knoten zurück und prüft, ob es dort weitere unbesuchte Nachbarn gibt. Wenn es welche gibt, werden diese erkundet; wenn nicht, wird der Weg zurückverfolgt. Dieser Zyklus von tiefer eintauchen und zurückverfolgen wird fortgesetzt, bis alle möglichen Pfade abgedeckt sind oder eine Ausstiegsbedingung erfüllt ist.
Handhabungszyklen
Graphen können Zyklen enthalten, also Pfade, die sich selbst wiederholen. Ohne entsprechende Vorkehrungen könnte das DFS die Knotenpunkte in diesen Zyklen endlos wieder besuchen. Indem jeder Knoten beim ersten Mal als besucht markiert wird, kann das DFS vermeiden, seine Schritte unnötig zurückzuverfolgen. Auf diese Weise bleibt das DFS auch in zyklischen Graphen effizient und vermeidet Endlosschleifen.
Umfassende Erkundung
Eines der Markenzeichen der DFS ist die Fähigkeit, eine Struktur vollständig zu erkunden. Der Algorithmus wird so lange fortgesetzt, bis jeder Knotenpunkt besucht worden ist. Das ist besonders nützlich, wenn du sicherstellen musst, dass keine potenzielle Lösung übersehen wird, z. B. beim Lösen von Rätseln, beim Erkunden von Entscheidungsbäumen oder beim Navigieren durch Labyrinthe.
Depth-First-Suche in Python implementieren
Es gibt zwei Möglichkeiten, eine Deep-First-Suche in Python zu implementieren: rekursiv und iterativ. Jeder Ansatz hat seine Vor- und Nachteile, und die Wahl hängt oft von der Größe des Graphen und dem Problem ab, das du lösen willst.
Um beide Methoden zu veranschaulichen, erstellen wir einen einfachen Entscheidungsbaum und verwenden DFS, um ihn zu durchlaufen. Wir werden Python für unser Beispiel verwenden. Du kannst jederzeit den Python-Programmierkurs besuchen, um deine Python-Kenntnisse aufzufrischen.
Nehmen wir einen binären Entscheidungsbaum als Beispiel. Hier ist eine einfache Baumstruktur, bei der jeder Knoten zwei untergeordnete Zweige hat:
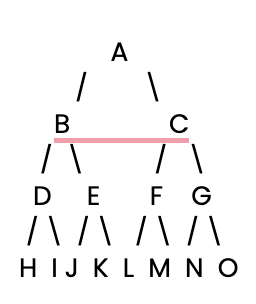
Definieren wir diesen Entscheidungsbaum in Python explizit als Wörterbuch.
# Define the decision tree as a dictionary
tree = {
'A': ['B', 'C'],
'B': ['D', 'E'],
'C': ['F', 'G'],
'D': ['H', 'I'],
'E': ['J', 'K'],
'F': ['L', 'M'],
'G': ['N', 'O'],
'H': [], 'I': [], 'J': [], 'K': [],
'L': [], 'M': [], 'N': [], 'O': []
}Rekursives DFS
Das DFS wird oft rekursiv implementiert. An jedem Knotenpunkt ruft das DFS seine Kindknoten so lange auf, bis es keine weiteren mehr zu besuchen gibt, und geht dann zurück. Hier ist eine rekursive DFS-Funktion, um den Baum zu durchlaufen.
# Recursive DFS function
def dfs_recursive(tree, node, visited=None):
if visited is None:
visited = set() # Initialize the visited set
visited.add(node) # Mark the node as visited
print(node) # Print the current node (for illustration)
for child in tree[node]: # Recursively visit children
if child not in visited:
dfs_recursive(tree, child, visited)
# Run DFS starting from node 'A'
dfs_recursive(tree, 'A')In dieser rekursiven Version beginnen wir am Wurzelknoten A und erkunden jeden Zweig, bevor wir zurückgehen, um die Alternativen zu erkunden. Wenn wir diesen Code ausführen, wird er den Weg ausgeben, den er bei der Erkundung des Baums genommen hat:
A
B
D
H
I
E
J
K
C
F
L
M
G
N
OIterative DFS
Bei sehr großen Entscheidungsbäumen kann die Rekursionstiefe von Python zu Problemen führen. In diesen Fällen können wir das DFS iterativ implementieren, indem wir einen Stapel verwenden, um die Knoten zu verwalten, die besucht werden müssen. So könnten wir das iterative DFS für denselben Entscheidungsbaum umsetzen:
# Iterative DFS function
def dfs_iterative(tree, start):
visited = set() # Track visited nodes
stack = [start] # Stack for DFS
while stack: # Continue until stack is empty
node = stack.pop() # Pop a node from the stack
if node not in visited:
visited.add(node) # Mark node as visited
print(node) # Print the current node (for illustration)
stack.extend(reversed(tree[node])) # Add child nodes to stack
# Run DFS starting from node 'A'
dfs_iterative(tree, 'A')Dieser iterative Ansatz umgeht die Grenzen der Rekursionstiefe, indem er den Stack manuell bearbeitet, was bei großen Bäumen oder tiefen Strukturen nützlich sein kann. Wenn du diesen Code ausführst, erhältst du die gleiche Ausgabe wie oben.
Wann sollte man rekursive versus iterative DFS verwenden?
Sowohl rekursive als auch iterative Ansätze für die Tiefensuche sind wertvolle Werkzeuge, aber die Wahl zwischen ihnen hängt von der Struktur des Graphen und deinen spezifischen Bedürfnissen ab. Schauen wir uns die Stärken und Grenzen der einzelnen Ansätze genauer an.
Rekursives DFS
Ich bevorzuge generell die Einfachheit und Eleganz der rekursiven DFS. Dieser Ansatz ist intuitiv und sauber.
Vorteile:
- Einfachheit: Der Code ist kompakt und spiegelt das Problem gut wider.
- Lesbarkeit: Einfacher zu verstehen, besonders bei kleinen bis mittelgroßen Problemen.
Nachteile:
- Grenze der Rekursionstiefe: Bei großen Graphen stößt du möglicherweise an die Rekursionstiefe von Python.
Rekursion ist ideal für Probleme, bei denen der Baum oder Graph relativ klein ist und bequem in die Rekursionstiefe von Python passt.
Iterative DFS
Die iterative DFS ist zwar etwas komplizierter zu schreiben, aber sie ist flexibler und kann größere Probleme bewältigen, ohne sich um Rekursionsgrenzen zu kümmern. Anstatt sich auf den Call Stack von Python zu verlassen, verwaltet das iterative DFS die zu untersuchenden Knoten explizit über einen Stack.
Vorteile:
- Keine Rekursionsgrenze: Durch die manuelle Verwaltung des Stacks wird die Rekursionstiefenbegrenzung von Python umgangen.
Nachteile:
- Mehr Code: Iteratives DFS erfordert mehr Einstellungen und kann weniger intuitiv sein.
- Lesbarkeit: Der Code ist oft etwas ausführlicher, was es schwieriger macht, ihm zu folgen.
Der iterative Ansatz eignet sich am besten für große oder komplexe Probleme, bei denen die Rekursionstiefe ein Problem darstellt. Sie ist auch nützlich, wenn du mehr Kontrolle über das Traversal brauchst.
Zeit und Raum Komplexität
DFS ist ein effizienter Algorithmus, aber seine Leistung hängt von der Größe und Struktur des Graphen ab, den er erforscht. Wie lange das DFS braucht und wie viel Speicher es verbraucht, hängt von der Anzahl der Knoten ab, die es besucht, sowie von den Verbindungen zwischen ihnen.
Wir verwenden die BigO-Notation, um über Komplexität zu sprechen. Eine Auffrischung der Big O-Notation findest du unter Big O Notation and Time Complexity Guide: Intuition und Mathematik.
Zeitliche Komplexität
Die Zeitkomplexität des DFS ist definiert als O(V + E), wobei V die Anzahl der Knoten und E die Anzahl der Verbindungen (genannt "Kanten") ist. Das DFS besucht jeden Knoten und jede Verbindung einmal. Die Gesamtzeit, die das DFS benötigt, hängt also davon ab, wie viele Knotenpunkte und Verbindungen es gibt.
Raumkomplexität
Der Platzbedarf des DFS hängt davon ab, wie viele Knoten der Algorithmus zu einem bestimmten Zeitpunkt im Blick hat. Sowohl das rekursive als auch das iterative DFS verwenden einen Stapel, um die Knoten zu verfolgen, die erforscht werden. Im schlimmsten Fall kann der verwendete Speicher alle Knoten des Graphen aufnehmen, was zu einer Raumkomplexität von O(V) führt.
Erkunde andere Möglichkeiten, die Komplexität von Algorithmen zu messen, im Tutorial Komplexität von Code mit Python analysieren.
Reale Anwendungen der Depth-First-Suche
Die DFS ist in vielen Bereichen nützlich, zum Beispiel in der Informatik, der KI und der Spieleentwicklung. In der folgenden Tabelle findest du einige gängige Anwendungen des DFS.
| Bewerbung | Beschreibung |
|---|---|
| Labyrinth lösen | Die DFS erkundet Wege in einem Labyrinth, indem sie in einen Weg eintaucht, bis sie eine Sackgasse erreicht, und dann zurückgeht, um andere Routen zu erkunden. Sie garantiert, dass ein Weg gefunden wird, auch wenn er nicht unbedingt der kürzeste ist. |
| Rätsel lösen | Bei vielen Rätseln, wie z. B. Sudoku oder dem N-Queens-Problem, muss die DFS mögliche Lösungen untersuchen und zurückgehen, wenn eine Konfiguration nicht funktioniert. |
| Pfadfinderei in Spielen | Das DFS hilft der KI in Strategiespielen, tiefe Zugfolgen zu erforschen und die Ergebnisse zu simulieren, um Entscheidungen zu treffen. |
| Zyklus-Erkennung | DFS erkennt Zyklen, indem es prüft, ob es bei der Erkundung von Pfaden in Graphen einen Knoten erneut besucht, was bei Aufgaben wie der Auflösung von Abhängigkeiten nützlich ist. |
| Topologische Sortierung | In gerichteten azyklischen Graphen ordnet DFS die Knoten auf der Grundlage von Abhängigkeiten, wie z.B. bei der Projektplanung, wo die Reihenfolge der Aufgaben wichtig ist. |
Depth-First-Suche im Vergleich. Andere Suchalgorithmen
Vergleichen wir DFS mit anderen bekannten Algorithmen wie Breadth-First Search, Dijkstra's Algorithm und A*.
Depth-First-Suche versus Breadth-First-Suche
Die Breadth-First-Suche (BFS) erkundet einen Graphen Ebene für Ebene und besucht alle Knoten in der aktuellen Tiefe, bevor sie zur nächsten Ebene weitergeht. BFS ist besonders nützlich, wenn es darum geht, den kürzesten Weg in einem ungewichteten Graphen zu finden. Allerdings kann das BFS viel Speicherplatz verbrauchen, vor allem in breiten Graphen, weil es alle Knoten auf jeder Ebene im Auge behalten muss. BFS eignet sich hervorragend für die Analyse sozialer Netzwerke oder einfache Routing-Probleme.
Die Tiefensuche hingegen ist nützlich, wenn das Ziel darin besteht, alle möglichen Pfade oder Lösungen zu erkunden, z. B. beim Lösen von Rätseln oder beim Finden von Zyklen in einem Graphen. Im Gegensatz zum BFS garantiert das DFS nicht den kürzesten Weg. Aber es ist speichereffizienter, da es nur den aktuellen Pfad speichert.
Du kannst mehr über die Breadth-First-Suche erfahren Breadth-First Search: A Beginner's Guide with Python Examples.
DFS versus Dijkstra-Algorithmus
Der Dijkstra-Algorithmus wurde entwickelt, um den kürzesten Weg in Graphen mit gewichteten Kanten zu finden, bei denen jede Verbindung zwischen Knoten mit Kosten verbunden ist. Dijkstra erkundet immer zuerst den kostengünstigsten Weg und stellt so sicher, dass der optimale Weg vom Startknoten zu jedem anderen Knoten gefunden wird. Allerdings kann es bei bestimmten einfachen Graphenuntersuchungen langsamer sein als das DFS. Das Dijkstra-Verfahren eignet sich perfekt für Aufgaben, bei denen es auf die Gewichtung der Kanten ankommt, wie z. B. bei Straßennetzen oder komplexeren Routing-Problemen.
Bei der Depth-First-Suche werden die Kantengewichte nicht berücksichtigt, sodass der optimale Pfad nicht garantiert werden kann. In ungewichteten Graphen oder wenn die Kantengewichte irrelevant sind, ist es jedoch schneller als das Dijkstra-Verfahren.
Mehr über Dijkstras Algorithmus erfährst du unter Implementing the Dijkstra Algorithm in Python: Ein Schritt-für-Schritt-Tutorial.
DFS gegen A*
A* (ausgesprochen "A-star") ist ein Algorithmus, der den Dijkstra-Algorithmus verbessert, indem er eine Heuristik zur Steuerung der Suche einbezieht. Das macht sie in vielen Fällen schneller und effizienter. A* balanciert zwischen der Erkundung der kostengünstigsten Pfade (wie bei Dijkstra) und dem direkten Ansteuern des Ziels, indem es eine Heuristik wie die geradlinige Entfernung zum Ziel verwendet. Das macht A* sehr effizient für Aufgaben wie die GPS-Navigation oder die Wegfindung in Videospielen.
Die Depth-First-Suche verwendet keine Heuristik, d.h. ihr fehlt die "Richtung", die A* verwendet, um das Ziel effizient zu erreichen. DFS eignet sich besser für Probleme, die eine gründliche Suche im gesamten Graphen oder Entscheidungsbaum erfordern, während A* besser geeignet ist, wenn der kürzeste Weg mit Hilfe einer Heuristik effizient gefunden werden muss.
Du kannst mehr über A* auf Wikipedia erfahren.
Häufige Fallstricke und wie du sie vermeidest
Bei der Tiefensuche können mehrere Probleme auftreten, insbesondere bei großen Graphen.
Besuchte Knoten werden nicht verfolgt
Ein Problem tritt auf, wenn du vergisst zu verfolgen, welche Knotenpunkte bereits besucht wurden. Das kann zu Endlosschleifen führen, besonders in Graphen, die Zyklen enthalten. Wenn das DFS Knotenpunkte erneut besucht, ohne zu prüfen, ob sie bereits erkundet wurden, kann es in einer Endlosschleife stecken bleiben. Um dies zu vermeiden, solltest du eine Liste der besuchten Knotenpunkte führen. Bevor du einen neuen Knoten besuchst, überprüfe, ob er bereits in der besuchten Menge enthalten ist. Wenn das der Fall ist, kannst du sie getrost überspringen und vermeiden, in die Falle zu gehen.
Stapelüberlauf im rekursiven DFS
In Python ist die Rekursionstiefe standardmäßig auf etwa 1.000 Ebenen begrenzt, was bedeutet, dass tief verschachtelte rekursive Aufrufe in großen Graphen einen RecursionError verursachen können. Um dies zu verhindern, können wir eine iterative DFS-Implementierung für große Graphen verwenden. Indem wir diesen Stapel als Liste führen, umgehen wir die Grenzen der Rekursionstiefe und können viel größere Graphen sicher handhaben.
Eine Lösung mit dem kürzesten Weg verwechseln
Es ist auch wichtig zu wissen, dass DFS nicht den kürzesten Weg zwischen zwei Knotenpunkten garantiert. Da das DFS einem Weg tiefgründig folgt, bevor es andere Wege erkundet, kann es zwar eine Lösung finden, aber es ist vielleicht nicht die direkteste.
Fazit
Die Tiefensuche ist ein leistungsstarker Algorithmus zum Erkunden und Durchlaufen von Graphen und Bäumen. Mit seiner Fähigkeit, tief in Pfade einzutauchen und alle Möglichkeiten zu erforschen, eignet er sich gut für eine Vielzahl von Problemen wie das Lösen von Labyrinthen, Rätseln und die Erkundung von Entscheidungsbäumen.
Wenn du dich für Suchalgorithmen interessierst, schau dir meine anderen Artikel in dieser Reihe an: Binäre Suche in Python: Ein kompletter Leitfaden für die effiziente Suche und Breadth-First Search: A Beginner's Guide with Python Examples. Das könnte dich auch interessieren: AVL Tree: Complete Guide With Python Implementation, und Introduction to Network Analysis in Python.

Ich bin promoviert und habe 13 Jahre Erfahrung in der Arbeit mit Daten in der biologischen Forschung. Ich entwickle Software in verschiedenen Programmiersprachen, darunter Python, MATLAB und R. Meine Leidenschaft ist es, meine Liebe zum Lernen mit der Welt zu teilen.
Depth-First-Suche in Python FAQs
Was ist Deep-First-Suche?
Die Tiefensuche ist ein Algorithmus, der zur Erkundung von Baum- oder Graphdatenstrukturen verwendet wird. Die Strategie sieht vor, dass ein Zweig so tief wie möglich erforscht wird, bevor alternative Zweige erkundet werden.
Wie unterscheidet sich die Deep-First-Suche von der Breadth-First-Suche?
DFS taucht tief in einen Zweig ein, bevor es zurückgeht, während BFS alle Nachbarknoten auf der aktuellen Ebene erkundet, bevor es zur nächsten Ebene geht.
Was sind die Vorteile von DFS?
DFS ist eine speichereffiziente Methode, um einen Graphen oder Baum umfassend zu erkunden.
Was sind die Nachteile von DFS?
DFS findet nicht garantiert den kürzesten Weg und berücksichtigt keine Graphgewichte.
Was sind einige praktische Anwendungen des DFS?
DFS kann beim Lösen von Labyrinthen und Rätseln, bei der Wegfindung und beim Crawlen im Internet eingesetzt werden.
