Track
Imagine you're exploring a vast cave system. You pick a tunnel and follow it as far as it goes, deeper and deeper, until you hit a dead end. Then, you backtrack to the last junction and try a new tunnel. This method of deep exploration, retracing your steps only when necessary, is a lot like depth-first search (DFS), a fundamental algorithm for navigating data structures like graphs and trees.
If you are data structures, algorithms, and problem-solving, DataCamp has you covered: Learn more about different data structures and the best algorithms to explore them with in the Data Structures and Algorithms in Python course and our Data Structures: A Comprehensive Guide With Python Examples tutorial.
What is Depth-First Search?
Depth-first search (DFS) is an algorithm used to traverse or search through a data structure, such as a graph or tree. The fundamental idea behind DFS is that it explores as far down a branch of the graph or tree as possible before backtracking to explore alternative branches. This approach contrasts with breadth-first search, which explores all nodes at the current depth level before moving on to the next. You can read about breadth-first search HERE.
Think of depth-first search as a way of exploring a maze: you choose a path and follow it until you hit a dead end. Once you reach the end of that path, you backtrack to the last decision point and try a different route. This deep exploration makes DFS an excellent choice when the goal is to fully explore a structure, especially one with many potential paths.

DFS is particularly useful in problems where you need to explore every possible solution.
A couple of examples include:
- Navigating decision trees in AI, where each branch represents a sequence of choices, and the goal is to evaluate all possible outcomes.
- Pathfinding problems, like navigating a game board or finding routes on a map, which require exhaustive searches.
DFS ensures that every node is visited once and that the algorithm covers the entire graph or tree.
Key Features of Depth-First Search in Python
Depth-first search has a systematic approach to exploring nodes and backtracking only when necessary. Let’s take a look at some of its key characteristics.
Recursive nature
At its core, DFS works recursively, which means it solves the problem by repeatedly calling itself as it explores deeper into the structure. When DFS dives into one branch, it explores it as deeply as possible before coming back up to explore other branches. This process of going deeper into a path and backtracking when there are no further options is ideally handled through recursion. Check out Understanding Recursive Functions in Python for an in-depth look at what recursive functions are and when they’re useful.
Backtracking
Backtracking is essential to DFS. When the algorithm reaches a node that has no unvisited neighbors, it retraces its steps to the previous node and checks if any other unvisited neighbors exist there. If there are, it will explore those; if not, it continues backtracking. This cycle of diving deeper and retracing continues until all possible paths have been covered or an exit condition has been met.
Handling cycles
Graphs can contain cycles, which are paths that loop back on themselves. Without proper precautions, DFS could endlessly revisit nodes in these cycles. By marking each node as visited the first time it's encountered, DFS can avoid retracing its steps unnecessarily. This way, even in cyclic graphs, DFS remains efficient and avoids infinite loops.
Comprehensive exploration
One of the hallmarks of DFS is its ability to fully explore a structure. The algorithm continues until every node has been visited. This is particularly useful when you need to ensure that no potential solution is missed, such as in solving puzzles, exploring decision trees, or navigating mazes.
Implementing Depth-First Search in Python
There are two main ways to implement a depth-first search in Python: recursively and iteratively. Each approach has its advantages and trade-offs, and the choice often depends on the size of the graph and the problem you're solving.
To illustrate both methods, let’s create a simple decision tree and use DFS to traverse it. We’ll use Python for our example. You can always check out the Python Programming skill track to refresh your Python skills.
Let's take a binary decision tree as an example. Here's a simple tree structure where each node has two child branches:
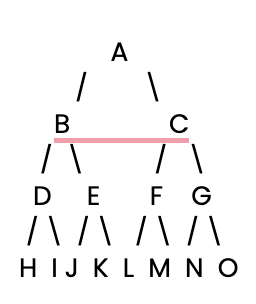
Let’s define this decision tree explicitly in Python as a dictionary.
# Define the decision tree as a dictionary
tree = {
'A': ['B', 'C'],
'B': ['D', 'E'],
'C': ['F', 'G'],
'D': ['H', 'I'],
'E': ['J', 'K'],
'F': ['L', 'M'],
'G': ['N', 'O'],
'H': [], 'I': [], 'J': [], 'K': [],
'L': [], 'M': [], 'N': [], 'O': []
}Recursive DFS
DFS is often implemented recursively. At each node, DFS calls itself on its child nodes until there are no more to visit, and then it backtracks. Here is a recursive DFS function to traverse the tree.
# Recursive DFS function
def dfs_recursive(tree, node, visited=None):
if visited is None:
visited = set() # Initialize the visited set
visited.add(node) # Mark the node as visited
print(node) # Print the current node (for illustration)
for child in tree[node]: # Recursively visit children
if child not in visited:
dfs_recursive(tree, child, visited)
# Run DFS starting from node 'A'
dfs_recursive(tree, 'A')In this recursive version, we start at the root node A and explore down each branch before backtracking to explore the alternatives. If we run this code, it will output the path it took while exploring this tree:
A
B
D
H
I
E
J
K
C
F
L
M
G
N
OIterative DFS
For very large decision trees, Python’s recursion depth limit could cause issues. In that cases, we can implement DFS iteratively, using a stack to manage the nodes that need to be visited. Here’s how we could implement iterative DFS for the same decision tree:
# Iterative DFS function
def dfs_iterative(tree, start):
visited = set() # Track visited nodes
stack = [start] # Stack for DFS
while stack: # Continue until stack is empty
node = stack.pop() # Pop a node from the stack
if node not in visited:
visited.add(node) # Mark node as visited
print(node) # Print the current node (for illustration)
stack.extend(reversed(tree[node])) # Add child nodes to stack
# Run DFS starting from node 'A'
dfs_iterative(tree, 'A')This iterative approach avoids recursion depth limits by manually handling the stack, which can be useful for large trees or deep structures. Running this code results in the same output as above.
When to Use Recursive Versus Iterative DFS
Both recursive and iterative approaches to depth-first search are valuable tools, but the choice between them depends on the structure of the graph and your specific needs. Let’s take a closer look at the strengths and limitations of each approach.
Recursive DFS
I generally prefer recursive DFS simplicity and elegance. This approach is intuitive and clean.
Pros:
- Simplicity: The code is compact and mirrors the problem well.
- Readability: Easier to understand, especially for small to medium-sized problems.
Cons:
- Recursion Depth Limit: For large graphs, you might hit Python’s recursion depth limit.
Recursion is ideal for problems where the tree or graph is relatively small and fits comfortably within Python's recursion depth.
Iterative DFS
While slightly more complex to write, iterative DFS is more flexible and can handle larger problems without worrying about recursion limits. Instead of relying on Python's call stack, iterative DFS explicitly manages the nodes to be explored via a stack.
Pros:
- No Recursion Limit: Managing the stack manually avoids Python's recursion depth limit.
Cons:
- More Code: Iterative DFS requires more setup and can be less intuitive.
- Readability: The code is often slightly more verbose, making it harder to follow.
The iterative approach is best for large or complex problems where recursion depth is a concern. It’s also useful when you need more control over the traversal.
Time and Space Complexity
DFS is an efficient algorithm, but its performance is influenced by the size and structure of the graph it’s exploring. How long DFS takes to run and how much memory it uses depends on the number of nodes it’s visiting as well as the connections between them.
We use BigO notation to talk about complexity. For a refresher on Big O notation, check out Big O Notation and Time Complexity Guide: Intuition and Math.
Time complexity
The time complexity of DFS is defined as O(V + E), where V is the number of nodes and E is the number of connections (called "edges"). DFS visits every node and every connection one time. So, the total time it takes for DFS depends on how many nodes and connections there are.
Space complexity
The space used in DFS depends on how many nodes the algorithm is keeping track of at any given moment. Both recursive and iterative DFS use a stack to keep track of nodes being explored. In the worst-case scenario, the memory used can hold all the nodes in the graph, leading to a space complexity of O(V).
Explore other ways of measuring algorithm complexity in the Analyzing Complexity of Code through Python tutorial.
Real-World Applications of Depth-First Search
DFS is useful across many fields, including computer science, AI, and game development. Check out the table below for some common applications of DFS.
| Application | Description |
|---|---|
| Maze Solving | DFS explores paths in a maze by diving into one path until reaching a dead end, then backtracks to explore other routes. It guarantees finding a path, though not necessarily the shortest one. |
| Puzzle Solving | Many puzzles, like Sudoku or the N-Queens problem, require DFS to explore potential solutions and backtrack when a configuration doesn’t work. |
| Pathfinding in Games | DFS helps AI in strategy games explore deep sequences of moves, simulating outcomes to inform decisions. |
| Cycle Detection | DFS detects cycles by checking if it revisits any node while exploring paths in graphs, useful in tasks like dependency resolution. |
| Topological Sorting | Used in directed acyclic graphs, DFS orders nodes based on dependencies, like in project scheduling where task order is important. |
Depth-First Search Vs. Other Search Algorithms
Let's compare DFS with other well-known algorithms like breadth-first search, Dijkstra’s Algorithm, and A*.
Depth-first search versus breadth-first search
Breadth-first search (BFS) explores a graph level by level, visiting all nodes at the current depth before moving to the next. BFS is particularly useful when the goal is to find the shortest path in an unweighted graph. However, BFS can use a lot of memory, especially in wide graphs, because it must keep track of all of the nodes at each level. BFS is an excellent choice for social network analysis or simple routing problems.
Depth-first search, on the other hand, is useful when the goal is to explore all possible paths or solutions, such as puzzle-solving or finding cycles in a graph. Unlike BFS, DFS doesn’t guarantee the shortest path. But it is more memory-efficient, as it only keeps track of the current path.
You can learn more about breadth-first search Breadth-First Search: A Beginner’s Guide with Python Examples.
DFS versus Dijkstra’s algorithm
Dijkstra’s algorithm is designed to find the shortest path in graphs with weighted edges, where each link between nodes has an associated cost. Dijkstra’s works by always exploring the lowest-cost path first, ensuring that the optimal path from the start node to any other node is found. However, it can be slower than DFS in certain simple graph explorations. Dijkstra’s is perfect for tasks where edge weights matter, such as road networks or more complex routing problems.
Depth-first search does not take edge weights into account, so it won't guarantee the optimal path. However, it’s faster than Dijkstra’s in unweighted graphs or when edge weights are irrelevant.
You can learn more about Dijkstra’s Algorithm in Implementing the Dijkstra Algorithm in Python: A Step-by-Step Tutorial.
DFS versus A*
A* (pronounced “A-star”) is an algorithm that improves upon Dijkstra’s by incorporating a heuristic to guide its search. This makes it faster and more efficient in many cases. A* balances between exploring the lowest-cost paths (like Dijkstra’s) and heading toward the goal directly, using a heuristic such as the straight-line distance to the goal. This makes A* highly efficient for tasks such as in GPS navigation or video game pathfinding.
Depth-first search does not use any heuristic, meaning it lacks the "direction" that A* uses to efficiently reach the goal. DFS is more suitable for problems that require a thorough search of the entire graph or decision tree, while A* is better when the shortest path needs to be found efficiently with the help of a heuristic.
Common Pitfalls and How to Avoid Them
When using depth-first search, several common issues can arise, particularly with large graphs.
Failing to track visited nodes
One issue arises when forgetting to track which nodes have already been visited. This can lead to infinite loops, especially in graphs that contain cycles. When DFS revisits nodes without checking if they've been explored, it can get stuck in an infinite loop. To avoid this, make sure to maintain a list of visited nodes. Before visiting a new node, check if it’s already in the visited set. If it is, you can safely skip it and avoid getting trapped.
Stack overflow in recursive DFS
In Python, recursion depth is limited to around 1,000 levels by default, which means deeply nested recursive calls in large graphs can cause a RecursionError. To prevent this, we can use an iterative DFS implementation for large graphs. By maintaining this stack as a list, we avoid the recursion depth limits and can safely handle much larger graphs.
Mistaking a solution for the shortest path
It’s also important to remember that DFS doesn’t guarantee the shortest path between two nodes. Since DFS follows one path deeply before backtracking to explore others, it may find a solution, but it might not be the most direct one.
Conclusion
Depth-first search is a powerful algorithm for exploring and traversing graphs and trees. With its ability to dive deep into paths and explore all possibilities, it’s well-suited for a variety of problems like maze solving, puzzle solving, and decision tree exploration.
If you’re interested in search algorithms, check out my other articles in this series: Binary Search in Python: A Complete Guide for Efficient Searching and Breadth-First Search: A Beginner’s Guide with Python Examples. You may also be interested in AVL Tree: Complete Guide With Python Implementation, and Introduction to Network Analysis in Python.

I am a PhD with 13 years of experience working with data in a biological research environment. I create software in several programming languages including Python, MATLAB, and R. I am passionate about sharing my love of learning with the world.
Depth-First Search in Python FAQs
What is depth-first search?
Depth-first search is an algorithm used for exploring tree or graph data structures. Its strategy prioritizes exploring one branch as deeply as possible before backtracking to investigate alternative branches.
How does depth-first search differ from breadth-first search?
DFS dives deep into one branch before backtracking, while BFS explores all neighbor nodes at the current level before moving to the next level.
What are some advantages to DFS?
DFS is a memory-efficient way to explore a graph or tree comprehensively.
What are some disadvantages to DFS?
DFS is not guaranteed to find the shortest path and doesn’t consider graph weights.
What are some real-world applications of DFS?
DFS can be applied to solving mazes and puzzles, pathfinding, and web crawling.
