Programa
Imagine que você está explorando um vasto sistema de cavernas. Você escolhe um túnel e o segue até o fim, cada vez mais fundo, até chegar a um beco sem saída. Em seguida, você volta para a última junção e tenta um novo túnel. Esse método de exploração profunda, refazendo suas etapas somente quando necessário, é muito parecido com a busca em profundidade (DFS), um algoritmo fundamental para navegar em estruturas de dados como gráficos e árvores.
Se você gosta de estruturas de dados, algoritmos e solução de problemas, o DataCamp tem tudo o que você precisa: Saiba mais sobre as diferentes estruturas de dados e os melhores algoritmos para explorá-las no curso Data Structures and Algorithms in Python (Estruturas de dados e algoritmos em Python ) e em nosso site Data Structures (Estruturas de dados): Um guia abrangente com exemplos em Python tutorial.
O que é a busca em profundidade (Depth-First Search)?
A pesquisa em profundidade (DFS) é um algoritmo usado para percorrer ou pesquisar uma estrutura de dados, como um gráfico ou uma árvore. A ideia fundamental por trás do DFS é que ele explora o máximo possível de um ramo do gráfico ou da árvore antes de voltar atrás para explorar ramos alternativos. Essa abordagem contrasta com a pesquisa de amplitude em primeiro lugar, que explora todos os nós no nível de profundidade atual antes de passar para o próximo. Você pode ler sobre a pesquisa de amplitude em primeiro lugar AQUI.
Pense na busca em profundidade como uma forma de explorar um labirinto: você escolhe um caminho e o segue até chegar a um beco sem saída. Quando chegar ao final desse caminho, você voltará ao último ponto de decisão e tentará uma rota diferente. Essa exploração profunda torna o DFS uma excelente opção quando o objetivo é explorar completamente uma estrutura, especialmente uma com muitos caminhos potenciais.

O DFS é particularmente útil em problemas em que você precisa explorar todas as soluções possíveis.
Alguns exemplos incluem:
- Navegar em árvores de decisão em IA, onde cada ramo representa uma sequência de escolhas e o objetivo é avaliar todos os resultados possíveis.
- Problemas de localização de caminhos, como navegar em um tabuleiro de jogo ou encontrar rotas em um mapa, que exigem pesquisas exaustivas.
O DFS garante que cada nó seja visitado uma vez e que o algoritmo cubra todo o gráfico ou árvore.
Principais recursos da pesquisa em profundidade em Python
A busca em profundidade tem uma abordagem sistemática para explorar os nós e voltar atrás somente quando necessário. Vamos dar uma olhada em algumas de suas principais características.
Natureza recursiva
Em sua essência, o DFS funciona de forma recursiva, o que significa que ele resolve o problema chamando a si mesmo repetidamente à medida que explora mais profundamente a estrutura. Quando o DFS mergulha em um ramo, ele o explora o mais profundamente possível antes de voltar a explorar outros ramos. Esse processo de se aprofundar em um caminho e voltar atrás quando não há mais opções é idealmente tratado por meio de recursão. Confira o artigo Understanding Recursive Functions in Python (Entendendo as funções recursivas em Python ) para que você tenha uma visão detalhada do que são funções recursivas e quando elas são úteis.
Retrocesso
O retrocesso é essencial para o DFS. Quando o algoritmo chega a um nó que não tem vizinhos não visitados, ele refaz seus passos até o nó anterior e verifica se há algum outro vizinho não visitado. Se houver, ele os explorará; caso contrário, continuará retrocedendo. Esse ciclo de mergulho mais profundo e retrocesso continua até que todos os caminhos possíveis tenham sido percorridos ou uma condição de saída tenha sido atendida.
Ciclos de manuseio
Os gráficos podem conter ciclos, que são caminhos que se repetem. Sem as devidas precauções, o DFS poderia revisitar infinitamente os nós nesses ciclos. Ao marcar cada nó como visitado na primeira vez que ele é encontrado, o DFS pode evitar que você refaça seus passos desnecessariamente. Dessa forma, mesmo em gráficos cíclicos, o DFS permanece eficiente e evita loops infinitos.
Exploração abrangente
Uma das marcas registradas do DFS é sua capacidade de explorar completamente uma estrutura. O algoritmo continua até que todos os nós tenham sido visitados. Isso é particularmente útil quando você precisa garantir que nenhuma solução potencial seja perdida, como na solução de quebra-cabeças, na exploração de árvores de decisão ou na navegação em labirintos.
Implementação da busca em profundidade em Python
Há duas maneiras principais de implementar uma busca em profundidade em Python: recursivamente e iterativamente. Cada abordagem tem suas vantagens e desvantagens, e a escolha geralmente depende do tamanho do gráfico e do problema que você está resolvendo.
Para ilustrar os dois métodos, vamos criar uma árvore de decisão simples e usar o DFS para percorrê-la. Usaremos o Python em nosso exemplo. Você sempre pode conferir o curso de habilidades em programação Python para atualizar suas habilidades em Python.
Vamos usar uma árvore de decisão binária como exemplo. Aqui está uma estrutura de árvore simples em que cada nó tem dois ramos filhos:
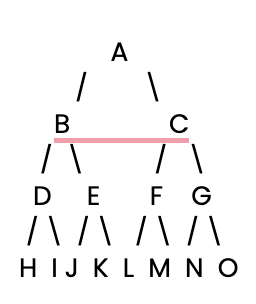
Vamos definir essa árvore de decisão explicitamente em Python como um dicionário.
# Define the decision tree as a dictionary
tree = {
'A': ['B', 'C'],
'B': ['D', 'E'],
'C': ['F', 'G'],
'D': ['H', 'I'],
'E': ['J', 'K'],
'F': ['L', 'M'],
'G': ['N', 'O'],
'H': [], 'I': [], 'J': [], 'K': [],
'L': [], 'M': [], 'N': [], 'O': []
}DFS recursivo
O DFS geralmente é implementado de forma recursiva. Em cada nó, o DFS chama a si mesmo em seus nós filhos até que não haja mais nenhum a ser visitado e, em seguida, volta atrás. Aqui está uma função DFS recursiva para percorrer a árvore.
# Recursive DFS function
def dfs_recursive(tree, node, visited=None):
if visited is None:
visited = set() # Initialize the visited set
visited.add(node) # Mark the node as visited
print(node) # Print the current node (for illustration)
for child in tree[node]: # Recursively visit children
if child not in visited:
dfs_recursive(tree, child, visited)
# Run DFS starting from node 'A'
dfs_recursive(tree, 'A')Nessa versão recursiva, começamos no nó raiz A e exploramos cada ramo antes de voltarmos para explorar as alternativas. Se executarmos esse código, ele exibirá o caminho que você percorreu ao explorar essa árvore:
A
B
D
H
I
E
J
K
C
F
L
M
G
N
ODFS iterativo
Para árvores de decisão muito grandes, o limite de profundidade de recursão do Python pode causar problemas. Nesses casos, podemos implementar o DFS de forma iterativa, usando uma pilha para gerenciar os nós que precisam ser visitados. Veja como poderíamos implementar o DFS iterativo para a mesma árvore de decisão:
# Iterative DFS function
def dfs_iterative(tree, start):
visited = set() # Track visited nodes
stack = [start] # Stack for DFS
while stack: # Continue until stack is empty
node = stack.pop() # Pop a node from the stack
if node not in visited:
visited.add(node) # Mark node as visited
print(node) # Print the current node (for illustration)
stack.extend(reversed(tree[node])) # Add child nodes to stack
# Run DFS starting from node 'A'
dfs_iterative(tree, 'A')Essa abordagem iterativa evita limites de profundidade de recursão manipulando manualmente a pilha, o que pode ser útil para árvores grandes ou estruturas profundas. A execução desse código resulta na mesma saída que a anterior.
Quando usar DFS recursivo versus Iterativo
As abordagens recursivas e iterativas da busca em profundidade são ferramentas valiosas, mas a escolha entre elas depende da estrutura do gráfico e de suas necessidades específicas. Vamos dar uma olhada mais de perto nos pontos fortes e nas limitações de cada abordagem.
DFS recursivo
Em geral, prefiro a simplicidade e a elegância do DFS recursivo. Essa abordagem é intuitiva e limpa.
Prós:
- Simplicidade: O código é compacto e reflete bem o problema.
- Legibilidade: Mais fácil de entender, especialmente para problemas de pequeno e médio porte.
Contras:
- Limite de profundidade de recursão: Em gráficos grandes, você pode atingir o limite de profundidade de recursão do Python.
A recursão é ideal para problemas em que a árvore ou o gráfico é relativamente pequeno e se encaixa confortavelmente na profundidade de recursão do Python.
DFS iterativo
Embora seja um pouco mais complexo de escrever, o DFS iterativo é mais flexível e pode lidar com problemas maiores sem se preocupar com limites de recursão. Em vez de depender da pilha de chamadas do Python, o DFS iterativo gerencia explicitamente os nós a serem explorados por meio de uma pilha.
Prós:
- Sem limite de recursão: O gerenciamento manual da pilha evita o limite de profundidade de recursão do Python.
Contras:
- Mais códigos: O DFS iterativo requer mais configuração e pode ser menos intuitivo.
- Legibilidade: O código geralmente é um pouco mais detalhado, o que dificulta o acompanhamento.
A abordagem iterativa é melhor para problemas grandes ou complexos em que a profundidade da recursão é uma preocupação. Também é útil quando você precisa de mais controle sobre a passagem.
Complexidade de tempo e espaço
O DFS é um algoritmo eficiente, mas seu desempenho é influenciado pelo tamanho e pela estrutura do gráfico que está sendo explorado. O tempo de execução do DFS e a quantidade de memória que ele usa dependem do número de nós que ele está visitando, bem como das conexões entre eles.
Usamos a notação BigO para falar sobre complexidade. Para se atualizar sobre a notação Big O, consulte Guia de notação Big O e complexidade de tempo: Intuição e matemática.
Complexidade de tempo
A complexidade de tempo do DFS é definida como O(V + E), em que V é o número de nós e E é o número de conexões (chamadas de "bordas"). O DFS visita cada nó e cada conexão uma única vez. Portanto, o tempo total que você leva para o DFS depende de quantos nós e conexões existem.
Complexidade espacial
O espaço usado no DFS depende de quantos nós o algoritmo está controlando em um determinado momento. Tanto o DFS recursivo quanto o iterativo usam uma pilha para manter o controle dos nós que estão sendo explorados. Na pior das hipóteses, a memória usada pode conter todos os nós do gráfico, o que leva a uma complexidade de espaço de O(V).
Explore outras formas de medir a complexidade do algoritmo no tutorial Analisando a complexidade do código por meio do Python.
Aplicativos do mundo real da busca em profundidade primeiro
O DFS é útil em muitos campos, incluindo ciência da computação, IA e desenvolvimento de jogos. Confira na tabela abaixo alguns aplicativos comuns do DFS.
| Aplicativo | Descrição |
|---|---|
| Solução de labirintos | O DFS explora caminhos em um labirinto, mergulhando em um caminho até chegar a um beco sem saída e, em seguida, volta para explorar outras rotas. Ele garante que você encontre um caminho, embora não necessariamente o mais curto. |
| Solução de quebra-cabeças | Muitos quebra-cabeças, como o Sudoku ou o problema das N-Queens, exigem que o DFS explore possíveis soluções e volte atrás quando uma configuração não funcionar. |
| Pathfinding em jogos | O DFS ajuda a IA em jogos de estratégia a explorar sequências profundas de movimentos, simulando resultados para informar decisões. |
| Detecção de ciclo | O DFS detecta ciclos verificando se ele revisita algum nó ao explorar caminhos em gráficos, o que é útil em tarefas como resolução de dependências. |
| Classificação topológica | Usado em gráficos acíclicos direcionados, o DFS ordena os nós com base em dependências, como na programação de projetos, em que a ordem das tarefas é importante. |
Pesquisa em profundidade versus pesquisa em profundidade. Outros algoritmos de pesquisa
Vamos comparar o DFS com outros algoritmos bem conhecidos, como a busca em primeiro lugar, o algoritmo de Dijkstra e o A*.
Pesquisa em profundidade versus pesquisa em largura
A pesquisa Breadth-first (BFS) explora um gráfico nível por nível, visitando todos os nós na profundidade atual antes de passar para a próxima. O BFS é particularmente útil quando o objetivo é encontrar o caminho mais curto em um gráfico não ponderado. No entanto, o BFS pode usar muita memória, especialmente em gráficos amplos, porque precisa manter o controle de todos os nós em cada nível. O BFS é uma excelente opção para análise de redes sociais ou problemas simples de roteamento.
A busca em profundidade, por outro lado, é útil quando o objetivo é explorar todos os caminhos ou soluções possíveis, como resolver quebra-cabeças ou encontrar ciclos em um gráfico. Ao contrário do BFS, o DFS não garante o caminho mais curto. No entanto, ele é mais eficiente em termos de memória, pois só mantém o controle do caminho atual.
Você pode saber mais sobre a busca em primeiro lugar Breadth-First Search: Um guia para iniciantes com exemplos em Python.
DFS versus algoritmo de Dijkstra
O algoritmo de Dijkstra foi projetado para encontrar o caminho mais curto em gráficos com bordas ponderadas, em que cada link entre os nós tem um custo associado. O Dijkstra funciona explorando sempre o caminho de menor custo primeiro, garantindo que o caminho ideal do nó inicial para qualquer outro nó seja encontrado. No entanto, ele pode ser mais lento do que o DFS em determinadas explorações simples de gráficos. O Dijkstra é perfeito para tarefas em que os pesos das bordas são importantes, como redes rodoviárias ou problemas de roteamento mais complexos.
A busca em profundidade não leva em conta os pesos das bordas, portanto, não garante o caminho ideal. No entanto, ele é mais rápido do que o Dijkstra em gráficos não ponderados ou quando os pesos das bordas são irrelevantes.
Você pode saber mais sobre o Algoritmo de Dijkstra em Implementando o Algoritmo de Dijkstra em Python: Um tutorial passo a passo.
DFS versus A*
O A* (pronuncia-se "A-star") é um algoritmo que aprimora o de Dijkstra ao incorporar uma heurística para orientar sua pesquisa. Isso o torna mais rápido e mais eficiente em muitos casos. A* equilibra a exploração dos caminhos de menor custo (como o de Dijkstra) e a direção direta ao objetivo, usando uma heurística como a distância em linha reta até o objetivo. Isso faz com que o A* seja altamente eficiente para tarefas como navegação GPS ou localização de caminhos em videogames.
A busca em profundidade não usa nenhuma heurística, o que significa que ela não tem a "direção" que A* usa para atingir a meta com eficiência. O DFS é mais adequado para problemas que exigem uma pesquisa completa de todo o gráfico ou árvore de decisão, enquanto o A* é melhor quando o caminho mais curto precisa ser encontrado de forma eficiente com a ajuda de uma heurística.
Você pode saber mais sobre o A* na Wikipedia.
Armadilhas comuns e como evitá-las
Quando você usa a busca em profundidade, podem surgir vários problemas comuns, principalmente em gráficos grandes.
Falha no rastreamento de nós visitados
Um problema surge quando você se esquece de rastrear quais nós já foram visitados. Isso pode levar a loops infinitos, especialmente em gráficos que contêm ciclos. Quando o DFS revisita os nós sem verificar se eles foram explorados, ele pode ficar preso em um loop infinito. Para evitar isso, certifique-se de manter uma lista de nós visitados. Antes de visitar um novo nó, verifique se ele já está no conjunto visitado. Se for, você pode ignorá-lo com segurança e evitar ficar preso.
Estouro de pilha em DFS recursivo
No Python, a profundidade da recursão é limitada a cerca de 1.000 níveis por padrão, o que significa que chamadas recursivas profundamente aninhadas em gráficos grandes podem causar um RecursionError. Para evitar isso, podemos usar uma implementação DFS iterativa para gráficos grandes. Ao manter essa pilha como uma lista, evitamos os limites de profundidade de recursão e podemos lidar com segurança com gráficos muito maiores.
Confundir uma solução com o caminho mais curto
Também é importante lembrar que o DFS não garante o caminho mais curto entre dois nós. Como o DFS segue um caminho profundamente antes de voltar para explorar outros, ele pode encontrar uma solução, mas talvez não seja a mais direta.
Conclusão
A busca em profundidade é um algoritmo avançado para explorar e percorrer gráficos e árvores. Com sua capacidade de se aprofundar em caminhos e explorar todas as possibilidades, ele é adequado para uma variedade de problemas, como resolução de labirintos, quebra-cabeças e exploração de árvores de decisão.
Se você estiver interessado em algoritmos de pesquisa, confira meus outros artigos desta série: Pesquisa binária em Python: Um guia completo para uma pesquisa eficiente e Breadth-First Search: Um guia para iniciantes com exemplos em Python. Você também pode estar interessado em AVL Tree: Complete Guide With Python Implementation, e Introduction to Network Analysis in Python.

Sou PhD e tenho 13 anos de experiência trabalhando com dados em um ambiente de pesquisa biológica. Crio software em várias linguagens de programação, incluindo Python, MATLAB e R. Sou apaixonado por compartilhar meu amor pelo aprendizado com o mundo.
Perguntas frequentes sobre a pesquisa em profundidade em Python
O que é pesquisa de profundidade primeiro?
A busca em profundidade é um algoritmo usado para explorar estruturas de dados de árvores ou gráficos. Sua estratégia prioriza a exploração de um ramo o mais profundamente possível antes de voltar atrás para investigar ramos alternativos.
Como a busca em profundidade difere da busca em amplitude?
O DFS mergulha profundamente em um ramo antes de voltar atrás, enquanto o BFS explora todos os nós vizinhos no nível atual antes de passar para o próximo nível.
Quais são algumas das vantagens do DFS?
O DFS é uma maneira eficiente em termos de memória para explorar um gráfico ou uma árvore de forma abrangente.
Quais são algumas das desvantagens do DFS?
Não é garantido que o DFS encontre o caminho mais curto e não considera os pesos do gráfico.
Quais são alguns aplicativos do DFS no mundo real?
O DFS pode ser aplicado à solução de labirintos e quebra-cabeças, localização de caminhos e rastreamento da Web.
