Cursus
Imaginez que vous explorez un vaste réseau de grottes. Vous choisissez un tunnel et vous le suivez jusqu'au bout, de plus en plus profondément, jusqu'à ce que vous tombiez sur un cul-de-sac. Ensuite, vous revenez sur vos pas jusqu'à la dernière jonction et vous essayez un nouveau tunnel. Cette méthode d'exploration en profondeur, qui consiste à ne revenir sur ses pas que lorsque c'est nécessaire, ressemble beaucoup à la recherche en profondeur d'abord (DFS), un algorithme fondamental pour la navigation dans les structures de données telles que les graphes et les arbres.
Si vous aimez les structures de données, les algorithmes et la résolution de problèmes, DataCamp vous couvre : Apprenez-en plus sur les différentes structures de données et les meilleurs algorithmes pour les explorer dans le cours Structures de données et algorithmes en Python et dans notre site Structures de données : Un guide complet avec des exemples en Python tutorial.
Qu'est-ce que la recherche en profondeur ?
La recherche en profondeur (DFS) est un algorithme utilisé pour parcourir ou rechercher une structure de données, telle qu'un graphe ou un arbre. L'idée fondamentale de DFS est d'explorer une branche du graphe ou de l'arbre aussi loin que possible avant de revenir en arrière pour explorer d'autres branches. Cette approche contraste avec la recherche en profondeur, qui explore tous les nœuds du niveau de profondeur actuel avant de passer au suivant. Pour en savoir plus sur la recherche de type "breadth-first", cliquez ICI.
Pensez à la recherche en profondeur d'abord comme à une façon d'explorer un labyrinthe : vous choisissez un chemin et le suivez jusqu'à ce que vous tombiez sur une impasse. Lorsque vous arrivez au bout de ce chemin, vous revenez sur vos pas jusqu'au dernier point de décision et essayez un autre itinéraire. Cette exploration en profondeur fait de DFS un excellent choix lorsque l'objectif est d'explorer complètement une structure, en particulier une structure avec de nombreux chemins potentiels.

Le DFS est particulièrement utile dans les problèmes où vous devez explorer toutes les solutions possibles.
En voici quelques exemples :
- Navigation dans les arbres de décision en IA, où chaque branche représente une séquence de choix et où l'objectif est d'évaluer tous les résultats possibles.
- Les problèmes de recherche d'itinéraire, comme la navigation sur un plateau de jeu ou la recherche d'itinéraires sur une carte, qui nécessitent des recherches exhaustives.
La méthode DFS garantit que chaque nœud est visité une fois et que l'algorithme couvre l'ensemble du graphe ou de l'arbre.
Principales caractéristiques de la recherche en profondeur en Python
La recherche en profondeur a une approche systématique de l'exploration des nœuds et du retour en arrière uniquement lorsque cela est nécessaire. Examinons quelques-unes de ses principales caractéristiques.
Caractère récursif
Au fond, DFS fonctionne de manière récursive, ce qui signifie qu'il résout le problème en s'appelant lui-même à plusieurs reprises au fur et à mesure qu'il explore plus profondément la structure. Lorsque DFS plonge dans une branche, il l'explore aussi profondément que possible avant de remonter pour explorer d'autres branches. Ce processus d'approfondissement d'un chemin et de retour en arrière lorsqu'il n'y a plus d'autres options est idéalement géré par la récursivité. Consultez la rubrique Comprendre les fonctions récursives en Python pour un examen approfondi de ce que sont les fonctions récursives et de leur utilité.
Retour en arrière
Le retour en arrière est essentiel pour le DFS. Lorsque l'algorithme atteint un nœud qui n'a pas de voisins non visités, il revient sur ses pas jusqu'au nœud précédent et vérifie s'il existe d'autres voisins non visités à cet endroit. S'il y en a, il les explore ; sinon, il continue à revenir sur ses pas. Ce cycle d'approfondissement et de retour en arrière se poursuit jusqu'à ce que tous les chemins possibles aient été parcourus ou qu'une condition de sortie ait été remplie.
Cycles de manutention
Les graphes peuvent contenir des cycles, c'est-à-dire des chemins qui reviennent sur eux-mêmes. Sans précautions appropriées, DFS pourrait revisiter indéfiniment les nœuds dans ces cycles. En marquant chaque nœud comme visité la première fois qu'il est rencontré, DFS peut éviter de revenir inutilement sur ses pas. Ainsi, même dans les graphes cycliques, DFS reste efficace et évite les boucles infinies.
Exploration complète
L'une des caractéristiques de la DFS est sa capacité à explorer pleinement une structure. L'algorithme se poursuit jusqu'à ce que tous les nœuds aient été visités. Cette fonction est particulièrement utile lorsque vous devez vous assurer qu'aucune solution potentielle n'est manquée, par exemple lors de la résolution d'énigmes, de l'exploration d'arbres de décision ou de la navigation dans des labyrinthes.
Implémentation de la recherche en profondeur (Depth-First Search) en Python
Il existe deux façons principales de mettre en œuvre une recherche en profondeur en premier dans Python : de manière récursive et de manière itérative. Chaque approche a ses avantages et ses inconvénients, et le choix dépend souvent de la taille du graphique et du problème à résoudre.
Pour illustrer ces deux méthodes, créons un arbre de décision simple et utilisons DFS pour le parcourir. Nous utiliserons Python pour notre exemple. Vous pouvez toujours consulter le cursus de programmation Python pour rafraîchir vos compétences en Python.
Prenons l'exemple d'un arbre de décision binaire. Voici une structure arborescente simple où chaque nœud a deux branches enfantines :
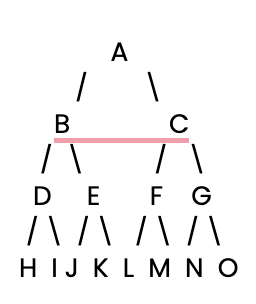
Définissons cet arbre de décision explicitement en Python sous la forme d'un dictionnaire.
# Define the decision tree as a dictionary
tree = {
'A': ['B', 'C'],
'B': ['D', 'E'],
'C': ['F', 'G'],
'D': ['H', 'I'],
'E': ['J', 'K'],
'F': ['L', 'M'],
'G': ['N', 'O'],
'H': [], 'I': [], 'J': [], 'K': [],
'L': [], 'M': [], 'N': [], 'O': []
}DFS récursif
Le système DFS est souvent mis en œuvre de manière récursive. À chaque nœud, DFS s'adresse à ses nœuds enfants jusqu'à ce qu'il n'y en ait plus à visiter, puis il revient en arrière. Voici une fonction DFS récursive pour parcourir l'arbre.
# Recursive DFS function
def dfs_recursive(tree, node, visited=None):
if visited is None:
visited = set() # Initialize the visited set
visited.add(node) # Mark the node as visited
print(node) # Print the current node (for illustration)
for child in tree[node]: # Recursively visit children
if child not in visited:
dfs_recursive(tree, child, visited)
# Run DFS starting from node 'A'
dfs_recursive(tree, 'A')Dans cette version récursive, nous partons du nœud racine A et explorons chaque branche avant de revenir en arrière pour explorer les alternatives. Si nous exécutons ce code, il affichera le chemin parcouru lors de l'exploration de cet arbre :
A
B
D
H
I
E
J
K
C
F
L
M
G
N
ODFS itératif
Pour les arbres de décision de très grande taille, la limite de profondeur de récursion de Python pourrait poser des problèmes. Dans ce cas, nous pouvons mettre en œuvre DFS de manière itérative, en utilisant une pile pour gérer les nœuds qui doivent être visités. Voici comment nous pourrions mettre en œuvre la méthode DFS itérative pour le même arbre de décision :
# Iterative DFS function
def dfs_iterative(tree, start):
visited = set() # Track visited nodes
stack = [start] # Stack for DFS
while stack: # Continue until stack is empty
node = stack.pop() # Pop a node from the stack
if node not in visited:
visited.add(node) # Mark node as visited
print(node) # Print the current node (for illustration)
stack.extend(reversed(tree[node])) # Add child nodes to stack
# Run DFS starting from node 'A'
dfs_iterative(tree, 'A')Cette approche itérative permet d'éviter les limites de profondeur de récursion en gérant manuellement la pile, ce qui peut s'avérer utile pour les grands arbres ou les structures profondes. L'exécution de ce code produit le même résultat que ci-dessus.
Quand utiliser le DFS récursif ou itératif ?
Les approches récursives et itératives de la recherche en profondeur sont toutes deux des outils précieux, mais le choix entre les deux dépend de la structure du graphe et de vos besoins spécifiques. Examinons de plus près les points forts et les limites de chaque approche.
DFS récursif
Je préfère généralement la simplicité et l'élégance du DFS récursif. Cette approche est intuitive et propre.
Pour :
- Simplicité: Le code est compact et reflète bien le problème.
- Lisibilité: Plus facile à comprendre, en particulier pour les problèmes de petite ou moyenne envergure.
Cons :
- Limite de profondeur de récursion: Pour les grands graphes, vous risquez de vous heurter à la limite de profondeur de récursion de Python.
La récursivité est idéale pour les problèmes où l'arbre ou le graphe est relativement petit et s'inscrit confortablement dans la profondeur de récursion de Python.
DFS itératif
Bien qu'elle soit légèrement plus complexe à écrire, la méthode DFS itérative est plus souple et permet de traiter des problèmes plus importants sans se soucier des limites de récursivité. Au lieu de s'appuyer sur la pile d'appels de Python, la DFS itérative gère explicitement les nœuds à explorer via une pile.
Pour :
- Pas de limite de récursivité: La gestion manuelle de la pile permet d'éviter la limite de profondeur de récursion de Python.
Cons :
- Plus de code: Le DFS itératif nécessite davantage de configuration et peut s'avérer moins intuitif.
- Lisibilité: Le code est souvent un peu plus verbeux, ce qui le rend plus difficile à suivre.
L'approche itérative est la meilleure pour les problèmes complexes ou de grande taille pour lesquels la profondeur de la récursivité est un problème. Elle est également utile lorsque vous avez besoin d'un meilleur contrôle sur la traversée.
Complexité du temps et de l'espace
DFS est un algorithme efficace, mais ses performances sont influencées par la taille et la structure du graphe qu'il explore. La durée d'exécution de DFS et la quantité de mémoire qu'il utilise dépendent du nombre de nœuds visités et des connexions entre eux.
Nous utilisons la notation BigO pour parler de la complexité. Pour en savoir plus sur la notation Big O, consultez le site Notation Big O et guide de la complexité temporelle : Intuition et mathématiques.
Complexité temporelle
La complexité temporelle de DFS est définie comme O(V + E), où V est le nombre de nœuds et E le nombre de connexions (appelées "arêtes"). DFS visite chaque nœud et chaque connexion une seule fois. Ainsi, la durée totale de DFS dépend du nombre de nœuds et de connexions.
Complexité de l'espace
L'espace utilisé dans DFS dépend du nombre de nœuds dont l'algorithme assure le suivi à un moment donné. Les systèmes DFS récursif et itératif utilisent tous deux une pile pour garder une trace des nœuds explorés. Dans le pire des cas, la mémoire utilisée peut contenir tous les nœuds du graphe, ce qui entraîne une complexité spatiale de O(V).
Explorez d'autres façons de mesurer la complexité des algorithmes dans le tutoriel Analyser la complexité du code grâce à Python.
Applications concrètes de la recherche en profondeur (Depth-First Search)
Le DFS est utile dans de nombreux domaines, notamment l'informatique, l'IA et le développement de jeux. Le tableau ci-dessous présente quelques applications courantes de DFS.
| Application | Description |
|---|---|
| Résolution de labyrinthes | DFS explore les chemins d'un labyrinthe en plongeant dans un chemin jusqu'à ce qu'il aboutisse à une impasse, puis en revenant sur ses pas pour explorer d'autres itinéraires. Il garantit la recherche d'un chemin, mais pas nécessairement le plus court. |
| Résolution d'énigmes | De nombreuses énigmes, comme le Sudoku ou le problème du N-Queens, nécessitent que DFS explore les solutions potentielles et revienne en arrière lorsqu'une configuration ne fonctionne pas. |
| Le cheminement dans les jeux | Dans les jeux de stratégie, DFS aide l'IA à explorer des séquences de mouvements profonds, en simulant les résultats pour éclairer les décisions. |
| Détection du cycle | DFS détecte les cycles en vérifiant s'il repasse par un nœud lors de l'exploration des chemins dans les graphes, ce qui est utile dans des tâches telles que la résolution des dépendances. |
| Tri topologique | Utilisé dans les graphes acycliques dirigés, DFS ordonne les nœuds en fonction des dépendances, comme dans la planification de projets où l'ordre des tâches est important. |
Recherche en profondeur d'abord contre recherche en profondeur d'abord. Autres algorithmes de recherche
Comparons DFS à d'autres algorithmes bien connus tels que la recherche en largeur, l'algorithme de Dijkstra et A*.
Recherche en profondeur d'abord contre recherche en profondeur d'abord (breadth-first)
La recherche en profondeur (BFS) explore un graphe niveau par niveau, en visitant tous les nœuds à la profondeur actuelle avant de passer à la suivante. BFS est particulièrement utile lorsque l'objectif est de trouver le chemin le plus court dans un graphe non pondéré. Cependant, BFS peut utiliser beaucoup de mémoire, en particulier dans les graphes larges, parce qu'il doit garder la trace de tous les nœuds à chaque niveau. BFS est un excellent choix pour l'analyse des réseaux sociaux ou les problèmes de routage simples.
La recherche en profondeur, en revanche, est utile lorsque l'objectif est d'explorer tous les chemins ou solutions possibles, comme la résolution d'énigmes ou la recherche de cycles dans un graphique. Contrairement à BFS, DFS ne garantit pas le chemin le plus court. Mais il est plus économe en mémoire, car il ne garde en mémoire que le chemin actuel.
Vous pouvez en savoir plus sur la recherche en profondeur Breadth-First Search (recherche en profondeur) : Un guide pour les débutants avec des exemples en Python.
DFS par rapport à l'algorithme de Dijkstra
L'algorithme de Dijkstra est conçu pour trouver le chemin le plus court dans les graphes aux arêtes pondérées, où chaque lien entre les nœuds a un coût associé. La méthode de Dijkstra consiste à toujours explorer le chemin le moins coûteux en premier, ce qui permet de trouver le chemin optimal entre le nœud de départ et n'importe quel autre nœud. Cependant, il peut être plus lent que DFS dans certaines explorations simples de graphes. La méthode de Dijkstra est parfaite pour les tâches où le poids des bords est important, comme les réseaux routiers ou les problèmes de routage plus complexes.
La recherche en profondeur ne prend pas en compte les poids des arêtes et ne garantit donc pas le chemin optimal. Cependant, il est plus rapide que celui de Dijkstra dans les graphes non pondérés ou lorsque les poids des arêtes ne sont pas pertinents.
Pour en savoir plus sur l'algorithme de Dijkstra, consultez le site Implementing the Dijkstra Algorithm in Python : Un tutoriel étape par étape.
DFS contre A*
A* (prononcé "A-star") est un algorithme qui améliore celui de Dijkstra en incorporant une heuristique pour guider sa recherche. Cela le rend plus rapide et plus efficace dans de nombreux cas. A* établit un équilibre entre l'exploration des chemins les moins coûteux (comme Dijkstra) et le fait de se diriger directement vers l'objectif, en utilisant une heuristique telle que la distance en ligne droite vers l'objectif. L'A* est donc très efficace pour des tâches telles que la navigation GPS ou le repérage dans les jeux vidéo.
La recherche en profondeur n'utilise aucune heuristique, ce qui signifie qu'elle n'a pas la "direction" qu'utilise A* pour atteindre efficacement l'objectif. DFS est plus adapté aux problèmes qui nécessitent une recherche approfondie de l'ensemble du graphe ou de l'arbre de décision, tandis que A* est meilleur lorsque le chemin le plus court doit être trouvé efficacement à l'aide d'une heuristique.
Les pièges les plus courants et comment les éviter
Lors de l'utilisation de la recherche en profondeur d'abord, plusieurs problèmes courants peuvent survenir, en particulier avec les grands graphes.
Le cursus ne permet pas de suivre les nœuds visités
Un problème se pose lorsqu'on oublie de repérer les nœuds qui ont déjà été visités. Cela peut conduire à des boucles infinies, en particulier dans les graphes qui contiennent des cycles. Lorsque DFS revisite des nœuds sans vérifier s'ils ont été explorés, il peut se retrouver coincé dans une boucle infinie. Pour éviter cela, veillez à maintenir une liste des nœuds visités. Avant de visiter un nouveau nœud, vérifiez s'il fait déjà partie de l'ensemble des nœuds visités. Si c'est le cas, vous pouvez l'ignorer en toute sécurité et éviter d'être pris au piège.
Dépassement de pile dans le DFS récursif
En Python, la profondeur de récursion est limitée à environ 1 000 niveaux par défaut, ce qui signifie que les appels récursifs profondément imbriqués dans les grands graphes peuvent provoquer une RecursionError. Pour éviter cela, nous pouvons utiliser une implémentation itérative de DFS pour les grands graphes. En conservant cette pile sous forme de liste, nous évitons les limites de profondeur de récursion et pouvons traiter en toute sécurité des graphes beaucoup plus grands.
Confondre une solution avec le chemin le plus court
Il est également important de rappeler que DFS ne garantit pas le chemin le plus court entre deux nœuds. Étant donné que DFS suit un chemin en profondeur avant de revenir sur ses pas pour en explorer d'autres, il peut trouver une solution, mais ce n'est pas forcément la plus directe.
Conclusion
La recherche en profondeur est un algorithme puissant qui permet d'explorer et de parcourir des graphes et des arbres. Avec sa capacité à plonger profondément dans les chemins et à explorer toutes les possibilités, il est bien adapté à une variété de problèmes tels que la résolution de labyrinthes, la résolution d'énigmes et l'exploration d'arbres de décision.
Si vous vous intéressez aux algorithmes de recherche, consultez les autres articles de cette série : Recherche binaire en Python : Un guide complet pour une recherche efficace et Breadth-First Search : Un guide pour les débutants avec des exemples en Python. Vous pouvez également être intéressé par AVL Tree : Complete Guide With Python Implementation, et Introduction à l'analyse des réseaux en Python.

Je suis titulaire d'un doctorat et j'ai 13 ans d'expérience dans le traitement des données dans un environnement de recherche biologique. Je crée des logiciels dans plusieurs langages de programmation, notamment Python, MATLAB et R. Je suis passionné par le partage de mon amour de l'apprentissage avec le monde.
FAQ sur la recherche en profondeur en Python
Qu'est-ce que la recherche en profondeur ?
La recherche en profondeur est un algorithme utilisé pour explorer les structures de données arborescentes ou graphiques. Sa stratégie consiste à explorer en priorité une branche aussi profondément que possible avant de revenir sur ses pas pour explorer d'autres branches.
En quoi la recherche en profondeur diffère-t-elle de la recherche en largeur ?
DFS plonge profondément dans une branche avant de revenir en arrière, tandis que BFS explore tous les nœuds voisins au niveau actuel avant de passer au niveau suivant.
Quels sont les avantages du DFS ?
Le DFS est un moyen efficace d'explorer un graphe ou un arbre de manière exhaustive.
Quels sont les inconvénients du DFS ?
DFS ne garantit pas de trouver le chemin le plus court et ne prend pas en compte les poids du graphe.
Quelles sont les applications réelles de DFS ?
Le DFS peut être appliqué à la résolution de labyrinthes et d'énigmes, à la recherche de chemins et à la navigation sur Internet.