Curso
Si tomamos muchas muestras aleatorias de casi cualquier tipo de distribución de datos, ocurre algo sorprendente. La media de esas muestras empieza a parecerse a una distribución normal: esa familiar curva en forma de campana. Eso es el teorema central del límite (TLC) en pocas palabras.
Es un gran problema en probabilidad y estadística, porque significa que podemos hacer predicciones precisas y sacar conclusiones sobre poblaciones enteras, aunque sólo analicemos pequeñas muestras.
Lo que hace que la CLT sea más útil es que funciona incluso si los datos originales no están distribuidos normalmente. Exploremos esto en detalle y veamos cómo podemos calcularlo.
¿Qué es el Teorema Central del Límite?
El teorema del límite central, o CLT, es una idea de la estadística que dice que si tomamos un montón de muestras aleatorias de cualquier población y observamos las medias de esas muestras, esas medias empezarán a formar una curva normal, en forma de campana, aunque la población original no parezca normal en absoluto.
Esto conecta con la ley de los grandes números, que nos dice que a medida que recogemos más datos, la media de nuestra muestra se acerca cada vez más a la media real de toda la población. La CLT va un paso más allá: nos dice que la media muestral se vuelve más precisa y que el patrón de esas medias se vuelve predecible. Nuestro curso de Introducción a la Estadística tiene ejercicios prácticos para que te familiarices con la relación y las diferencias entre la CLT y la ley de los grandes números, por si quieres profundizar en esta parte.
Una buena forma de ver esto en acción es lanzando un dado. Si la tiramos una sola vez, obtendremos un número aleatorio entre 1 y 6. Pero después de suficientes tiradas, la media se establecerá en torno a 3,5 (el verdadero valor medio de un dado justo). Hazlo repetidamente y la distribución de esas medias empezará a parecerse a una curva normal.
Fórmula del Teorema Central del Límite
He aquí la fórmula básica del teorema central del límite:
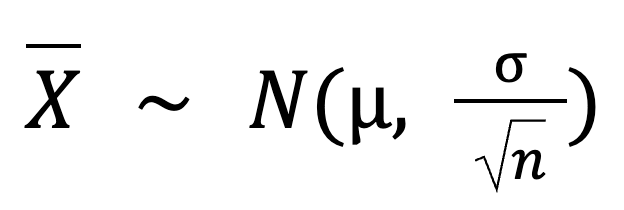
En esta fórmula:
-
Xes la distribución muestral de la media muestral, que sigue una distribución normal. -
Nes la distribución normal. -
𝜇es la media de la población. -
σes la desviación típica de la población. -
nes el tamaño de la muestra.
A medida que aumenta el tamaño de la muestra, disminuye la desviación típica de la distribución muestral. Cuantos más datos recojamos, más estrechamente se agruparán nuestras medias muestrales en torno a la verdadera media poblacional.
Condiciones del Teorema Central del Límite
Ahora bien, para que el teorema central del límite funcione como esperamos, hay que tener en cuenta algunas condiciones:
- Tamaño de la muestra suficientemente grande: El tamaño de la muestra tiene que ser lo suficientemente grande. Una muestra de 30 o más suele considerarse buena. Pero si la población de la que tomamos la muestra está sesgada o tiene muchos valores atípicos, puede que necesitemos una muestra mayor para que aparezca esa bonita curva en forma de campana.
- Muestras independientes e idénticamente distribuidas (i.i.d.): Las muestras que tomemos tienen que ser independientes e idénticamente distribuidas(i.i.d.). Esto significa que cada muestra se elige al azar y procede de la misma población. Si no es así, los resultados pueden no ser fiables.
- Varianza poblacional finita: La población que muestreamos debe tener una varianza finita. Si los datos proceden de una distribución con varianza infinita, como la distribución de Cauchy, la CLT no se aplicará a ellos.
Ejemplos del Teorema Central del Límite
Supongamos que queremos saber cuántas tazas de café se venden al día en una cafetería local. A lo largo de los años, el número de tazas vendidas cada día puede seguir una distribución similar a la que incluyo aquí. La mayoría de los días venden entre 80 y 120 tazas. Pero en días de gran afluencia, como fiestas o acontecimientos especiales, venden 150 o incluso 180 tazas. Los datos están un poco sesgados (desiguales) en este caso.
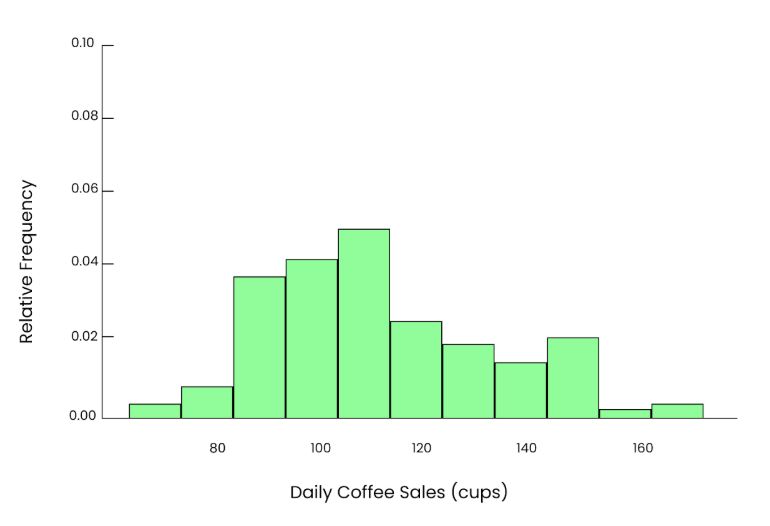
Gráfico desigual. Imagen del autor.
Digamos que tomamos una pequeña muestra. Elegimos al azar 5 días del año y miramos cuántas tazas se vendieron en esos días.
95, 102, 85, 110, 120La media que obtenemos de esta muestra es
Mean = 95+102+85+110+1205 = 102.4 cups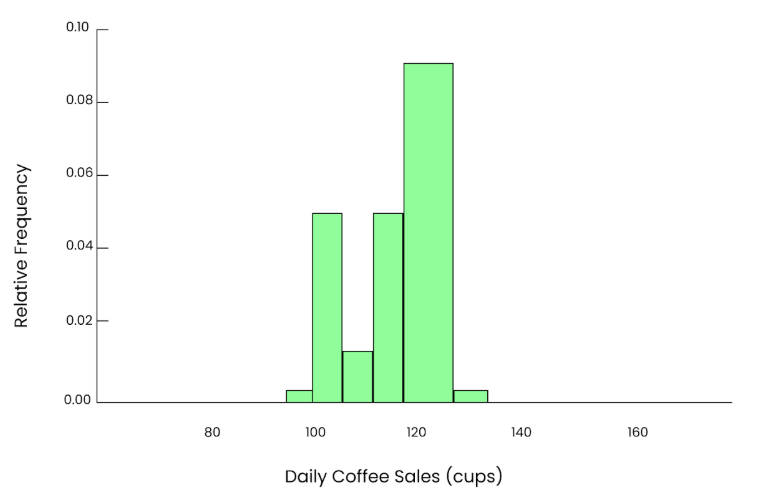
Gráfico de 5 tazas. Imagen del autor.
Eso nos da una estimación de la media de la población, pero como la muestra es pequeña, puede que no sea exacta. Si repetimos este proceso 10 veces, elegimos 5 días al azar cada vez, calculamos la media y anotamos los resultados. Las medias de 10 muestras serían:
97.6, 105.8, 93.4, 110.2, 99.0, 102.4, 101.2, 107.5, 96.3, 94.1Si trazamos estos valores en un histograma, veremos una forma de campana aproximada, pero aún así puede parecer desigual. Y la dispersión de estas medias es menor que la dispersión en la población.
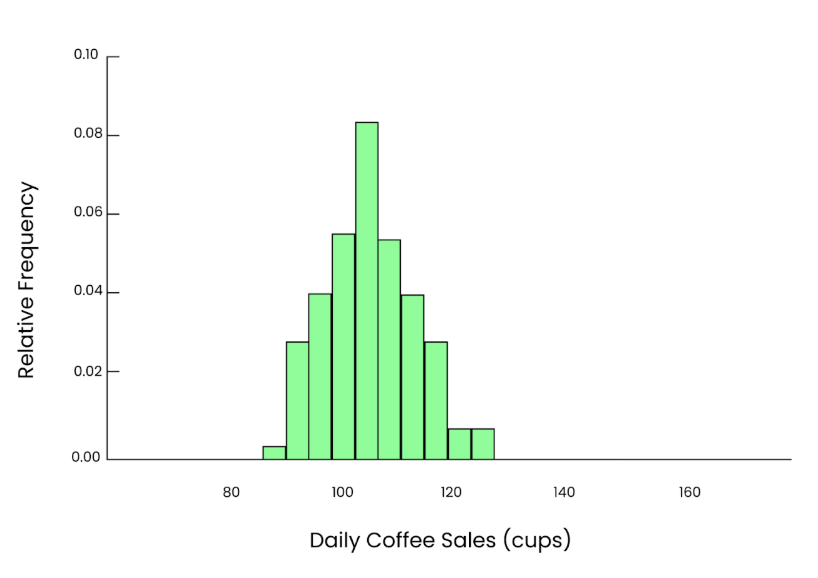
Gráfico de 10 tazas. Imagen del autor.
Ahora, tomemos una muestra mayor. Esta vez, seleccionamos aleatoriamente 50 días y calculamos el número medio de tazas vendidas:
98, 104, 87, 112, 105, 100, 108, 95, 102, 106,
92, 115, 97, 101, 109, 103, 96, 110, 104, 98,
100, 102, 89, 107, 94, 111, 108, 90, 100, 103,
106, 99, 96, 112, 105, 97, 100, 104, 93, 110,
107, 102, 95, 101, 99, 103, 109, 98, 94, 100Si calculamos la media de esta muestra, obtenemos
Mean = 101.2 cupsEsta estimación está mucho más cerca de la media poblacional de 100, y como el tamaño de nuestra muestra es mayor, es una estimación más precisa.
Si repetimos este proceso muchas veces, seleccionando cada vez 50 días al azar, calculando la media y trazando esas medias en un histograma, aunque los datos originales estuvieran sesgados, veremos una curva aparente y suave en forma de campana. Ése es el poder del teorema central del límite.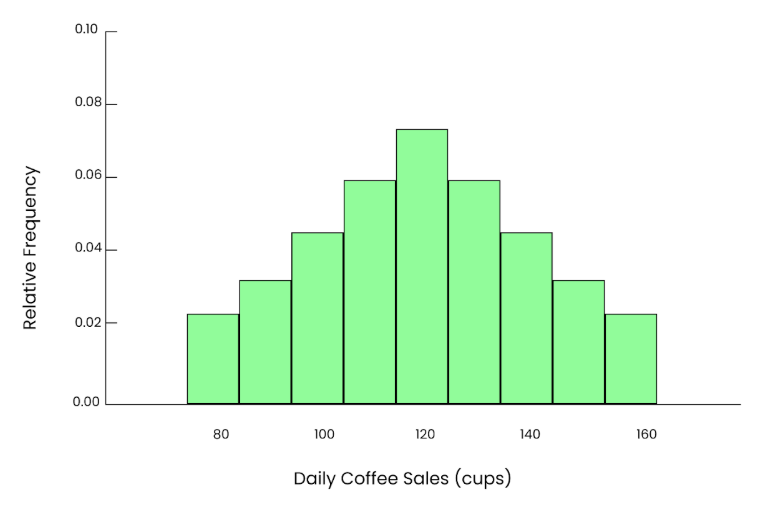
Gráfico par. Imagen del autor.
Incluso podemos calcular ese diferencial utilizando esta fórmula:
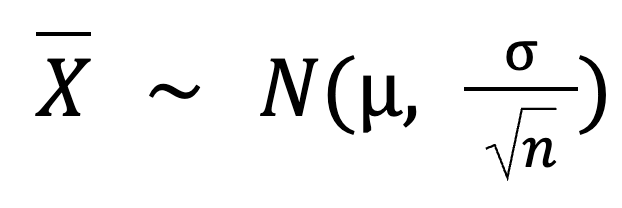 Toma:
Toma:
-
µ(media de la población) = 100 -
σ(desviación típica de la población) = 15 -
n(tamaño de la muestra) = 50
Por tanto, la desviación típica de nuestras medias muestrales es:
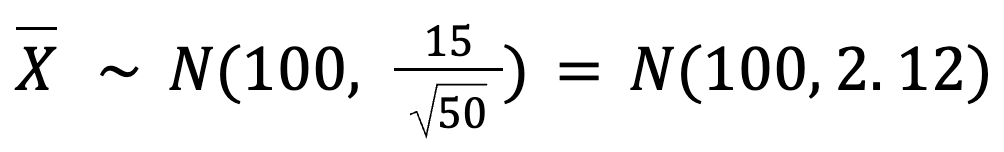
Esto nos indica que las medias muestrales estarán muy próximas a 100 tazas, con sólo una pequeña variación (en torno a 2,12 tazas).
Por qué es importante el Teorema Central del Límite
Ahora sabemos que los datos en el mundo real pueden ser extraños e impredecibles. Pero el teorema central del límite nos proporciona una forma fiable de comprender lo que ocurre y tomar mejores decisiones basándonos en ello. Comprendamos su importancia con más detalle.
Inferencia estadística
En estadística, el teorema del límite central es la razón por la que las pruebas paramétricas como las pruebas t, ANOVA y regresión funcionan como lo hacen. Estas pruebas se basan en la idea de que los datos de la muestra proceden de una población con características fijas.
Sin el teorema central del límite, no podríamos confiar en esas pruebas. Y debido a este teorema, las pruebas paramétricas suelen ser más potentes que las no paramétricas, que no hacen suposiciones sobre la distribución de los datos.
Aplicaciones industriales
También aparece en muchas situaciones del mundo real. En finanzas, los analistas lo utilizan para estimar la rentabilidad media de las acciones basándose en los resultados anteriores. En los sondeos y encuestas, hace predicciones sobre toda la población recogiendo una muestra de respuestas. En aprendizaje automático y big data, lo utilizamos cuando los modelos se entrenan sobre muestras. Por ejemplo, una aplicación de películas puede utilizar una muestra de la actividad de los usuarios para construir su sistema de recomendaciones.
Calculadora del Teorema Central del Límite
La desviación típica es un número que nos indica la dispersión de los valores respecto a la media. Cuando examinamos las medias muestrales (los promedios de diferentes muestras), queremos saber cuánto varían esos promedios. Para ello, podemos utilizar esta fórmula:
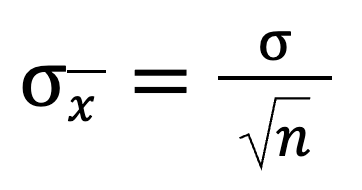
Esto nos dice que cuando dividimos la desviación típica de la población por la raíz cuadrada del tamaño de la muestra, obtenemos la desviación típica de la distribución muestral. A medida que aumenta el tamaño de la muestra, disminuye el valor global.
Veamos un ejemplo rápido:
| Tamaño de la muestra (n) | Media de la muestra (μₓ̄) | Std. Desviación (σₓ̄) |
|---|---|---|
| 5 | 17 | 1.788854 |
| 10 | 17 | 1.264911 |
| 25 | 17 | 0.800000 |
| 50 | 17 | 0.565685 |
| 100 | 17 | 0.400000 |
Puedes ver que la media se mantiene igual, pero la desviación típica sigue disminuyendo. Esto demuestra que cuanto mayor es la muestra, más precisa y coherente es.
El Teorema Central del Límite en la Ciencia de Datos
En la ciencia de datos, solemos tratar con muestras, no con poblaciones enteras. La CLT nos ayuda a comprender cómo se comportan esos resultados muestrales y nos dice que si tomamos suficientes muestras, sus medias empezarán a parecerse a una distribución normal, aunque los datos originales sean cualquier cosa menos eso.
Esto también tiene algunas grandes ventajas en el mundo real. En el aprendizaje automático, a menudo utilizamos técnicas como el bootstrapping para estimar valores. Gracias al CLT, podemos estar seguros de que esas estimaciones son exactas.
También es un elemento clave en las pruebas A/B. Cuando una empresa prueba dos versiones de una página web o función, el CLT nos ayuda a averiguar si los resultados son significativos o ruido aleatorio.
Incluso en el aprendizaje por refuerzo, en el que los sistemas aprenden por ensayo y error, la CLT plancha el caos. A medida que entran más datos, los promedios se hacen más estables, lo que ayuda al sistema a aprender más rápido y mejor.
Por último, también descubrirás el CLT en las pruebas de hipótesis y en el análisis de series temporales. Ayuda a los científicos de datos a probar ideas y seguir tendencias con más confianza.
Reflexiones finales
El teorema del límite central puede sonar técnico si eres nuevo en estadística, pero es una razón importante por la que podemos hacer cosas inteligentes con los datos. Convierte el azar en algo que podemos comprender y en lo que podemos confiar. De hecho, es uno de los componentes básicos de la modelización estadística y un conocimiento imprescindible para cualquiera que trabaje con datos.
Si quieres profundizar más, lee sobre la ley de los grandes números y las distribuciones de probabilidad: todo está relacionado.
Soy una estratega de contenidos a la que le encanta simplificar temas complejos. He ayudado a empresas como Splunk, Hackernoon y Tiiny Host a crear contenidos atractivos e informativos para su público.
Preguntas frecuentes sobre el Teorema Central del Límite
¿Puede utilizarse el teorema central del límite con datos no numéricos?
Sí, pero no directamente. El CLT se aplica a los datos numéricos, especialmente a las medias y las sumas. Sin embargo, para los datos categóricos u ordinales, puedes seguir utilizando principios similares convirtiendo los datos en forma numérica o utilizando otras técnicas estadísticas.
¿Cuál es la diferencia entre distribución muestral y distribución poblacional?
La distribución de la población describe el conjunto de datos completo, mientras que la distribución muestral se refiere a la distribución de los estadísticos muestrales (como las medias) procedentes del muestreo repetido.
¿Cómo afectan los valores atípicos al teorema central del límite?
Los valores atípicos aumentan la asimetría y la varianza, lo que significa que podemos necesitar una muestra de mayor tamaño para que la distribución muestral se aproxime a la normalidad.

