Ley de los Grandes Números: Una clave para comprender la incertidumbre

Un resultado por sí solo no te dice mucho. Supón que lanzas una moneda una vez y sale cara. Eso no prueba nada: podría haber caído así por casualidad. Pero si lanzas la moneda 100 veces, verás que salen cara y cruz en números aproximadamente iguales. Es entonces cuando la media empieza a tener sentido.

Y en esto consiste la ley de los grandes números. Cuantos más datos recopiles, más precisa será tu media. Te ayuda a ver el panorama general.

En esta guía, veremos qué significa la ley de los grandes números, cómo funciona en la vida real y por qué es tan útil cuando se trata de comprender pautas o tomar mejores decisiones a lo largo del tiempo.

¿Qué es la Ley de los Grandes Números?

Laley de los grandes números es un principio de la probabilidad y la estadística que explica cómo se comportan los averajes a medida que se recogen más datos. A medida que aumenta el tamaño de tu muestra, la media de esa muestra (llamadamedia muestral ) se acerca más a la media real de todo el grupo (llamada media poblacional).

En el mundo real, no solemos tener acceso a los datos de toda una población. En cambio, tomamos una muestra como la de encuestar a 1.000 votantes, en lugar de a los 300 millones de personas. La ley de los grandes números nos da la seguridad de que, con suficientes datos, la media muestral se aproximará a la real.

A medida que crece la muestra, la variación aleatoria empieza a anularse. Los valores atípicos tienen menos impacto, y la media se vuelve más estable y predecible.

Hay dos versiones principales de la ley, y difieren en la intensidad con que garantizan este efecto:

Ley débil (convergencia en probabilidad)

La ley débil de los grandes números dice que la media muestral probablemente se acerca a la media poblacional a medida que aumenta el tamaño de la muestra. Cuantos más datos recopiles, menos probable será que tu media se aleje mucho de la media.

Por ejemplo, lanzas una moneda al aire. A medida que das la vuelta más veces, la proporción entre cara y cruz se acerca al 50/50. Puede que no aterrice perfectamente, pero se acerca bastante, y de eso trata la ley débil.

Ley fuerte (convergencia casi segura)

La ley fuerte de los grandes números va un paso más allá. Dice que la media muestral se acercará a la media poblacional y se mantendrá en ella casi con toda seguridad, no sólo probablemente.

En términos sencillos: si sigues lanzando esa moneda justa eternamente, la proporción cara-cola no se acercará al 50/50; se asentará ahí. Así pues, esta ley nos da una certeza casi total de que las medias a largo plazo reflejan la verdad, salvo raras excepciones.

Ejemplos reales de la ley en el trabajo

Veamos algunos ejemplos de la vida real para comprender cómo funciona esta ley:

Lanzamiento de monedas o dados

Imagina que tiras tres veces un dado normal de seis caras. Puedes obtener resultados como 6, 2 y 5. La media es de 4,3, superior al valor esperado de 3,5. Pero ahora tiras el dado 100 veces, y luego 1.000 veces. A medida que aumenta el número de tiradas, tu media se acerca a 3,5. La ley de los grandes números suaviza la aleatoriedad a lo largo del tiempo.

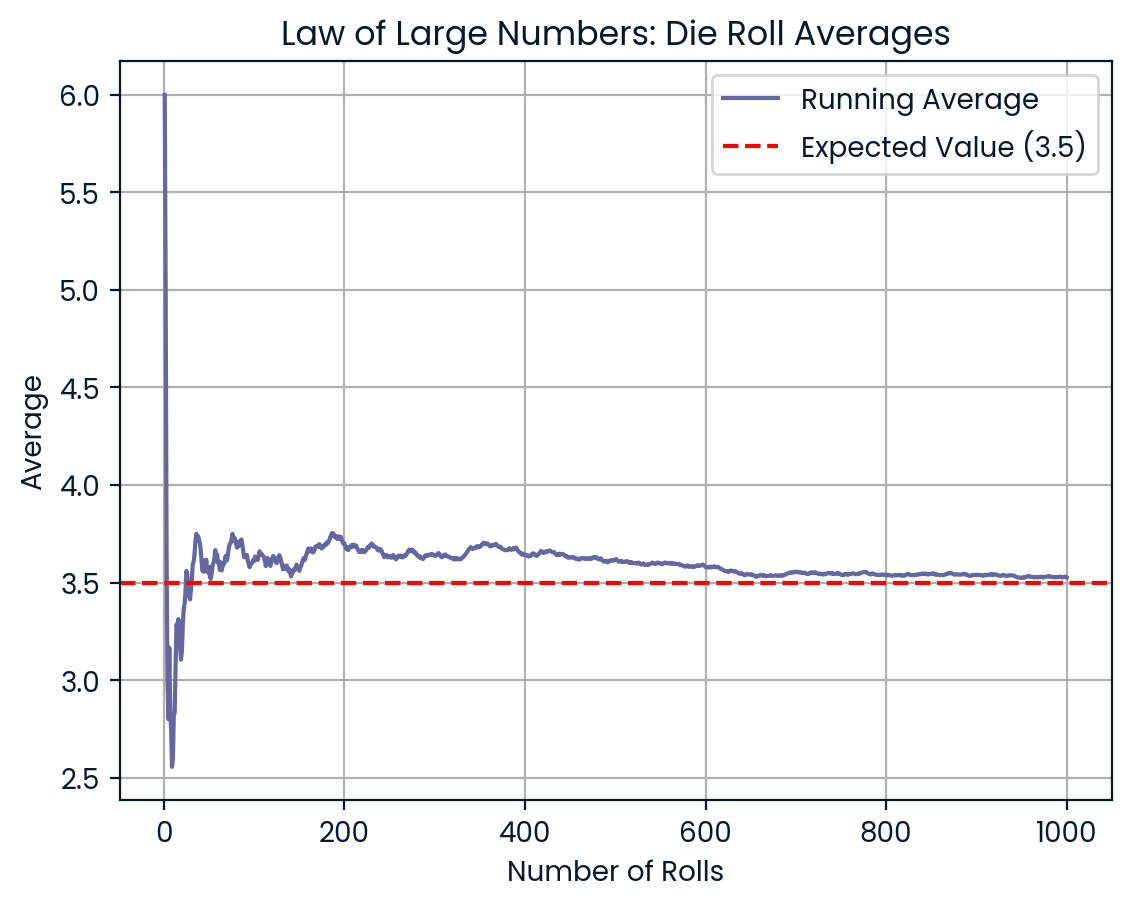
Más tiradas hacen que la media se acerque a 3,5. Imagen del autor.

Estadísticas deportivas

Los deportistas pueden tener días buenos y días malos. Un quarterback puede completar 9 de cada 10 pases en un partido, un impresionante 90%. Pero eso no significa que siempre jueguen a ese nivel.

A lo largo de toda una temporada, con cientos de lanzamientos, el porcentaje de finalización empieza a nivelarse. Esa estadística de toda la temporada da una idea mucho mejor de la capacidad real del jugador.

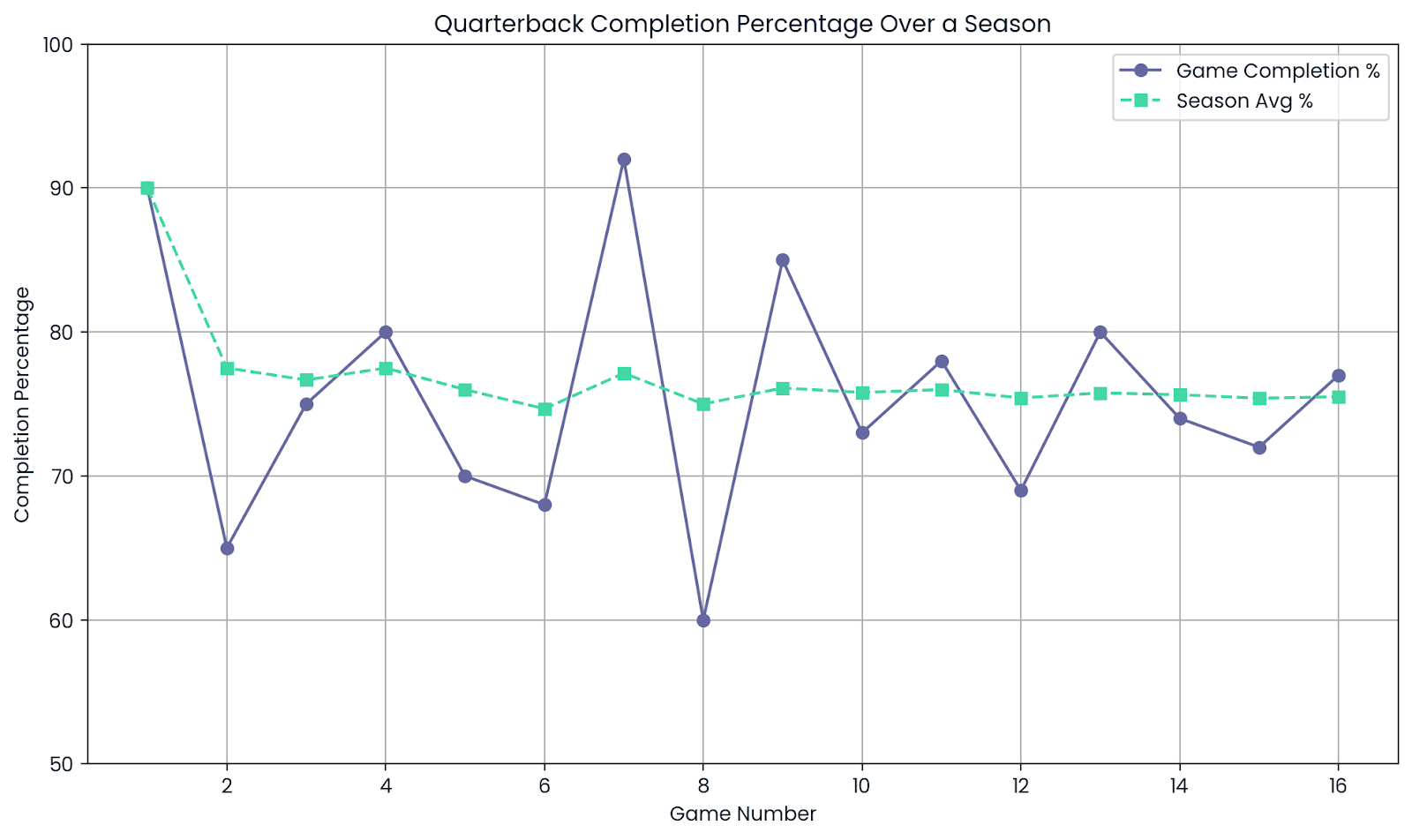
Media. Imagen del autor.

Agrupación de riesgos del sector asegurador 

Las compañías de seguros no saben exactamente cuánto les costará una persona. Algunas personas no utilizan ningún tipo de atención médica, mientras que otras sí.

Pero cuando observas a un grupo grande de personas, esos altibajos se equilibran. Al agrupar el riesgo entre miles de asegurados, las aseguradoras pueden predecir el coste medio con mayor precisión.

Esto les permite fijar precios justos (primas) al tiempo que se mantienen financieramente estables.

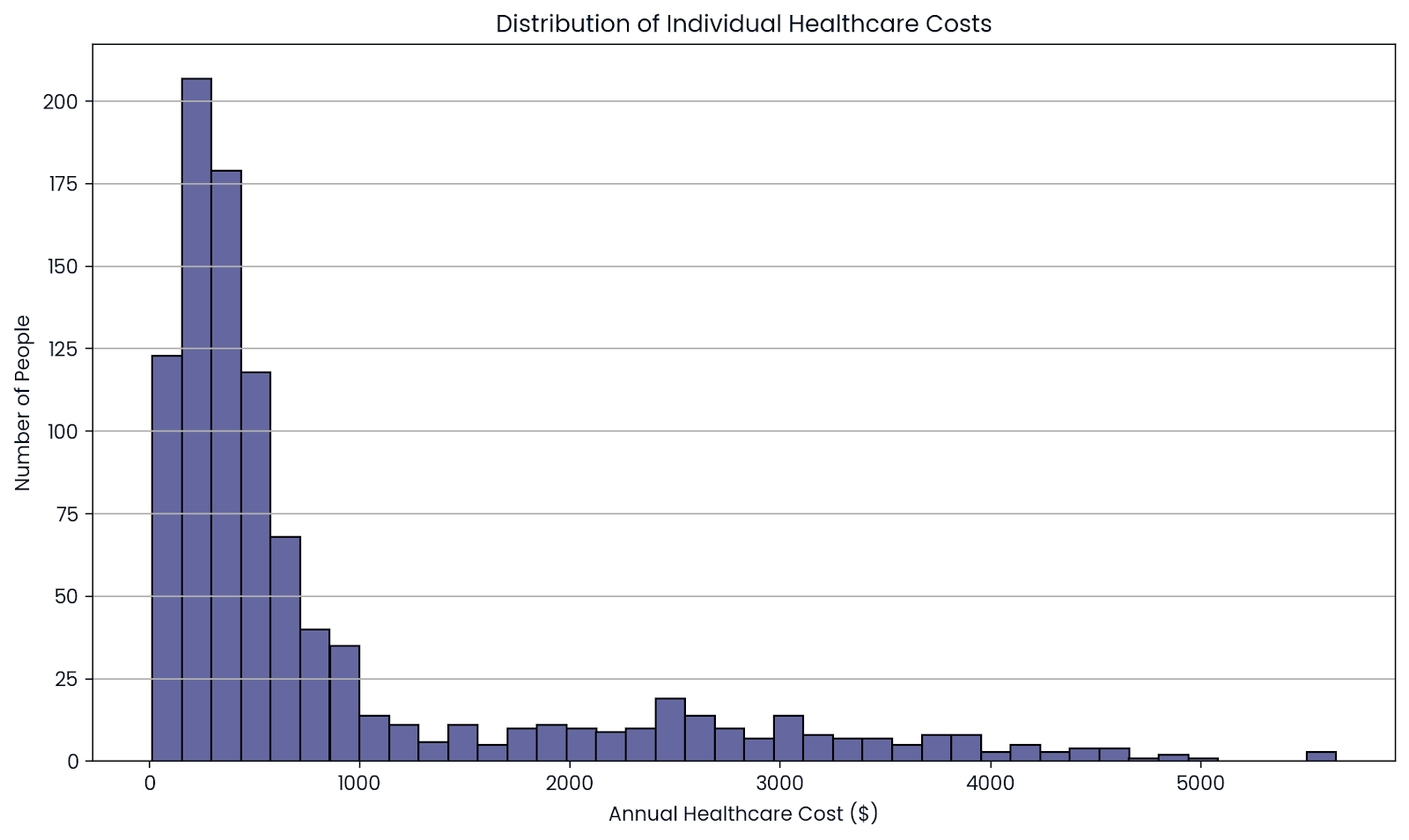
La media de muchas personas muestra el coste real. Imagen del autor.

Juegos de casino y ventaja de la casa

Los casinos crean una ligera ventaja en todos los juegos. Si juegas al blackjack, puedes ganar cinco manos seguidas o perder diez. Pero en miles de partidas, el resultado medio favorece al casino.

Por ejemplo, si la ventaja de la casa es del 0,5%, entonces, con el tiempo, el casino espera ganar 50 céntimos por cada 100 $ apostados de media. Puede que eso no ocurra en una sesión corta, pero a lo largo de millones de jugadas, se acumula exactamente como se esperaba.

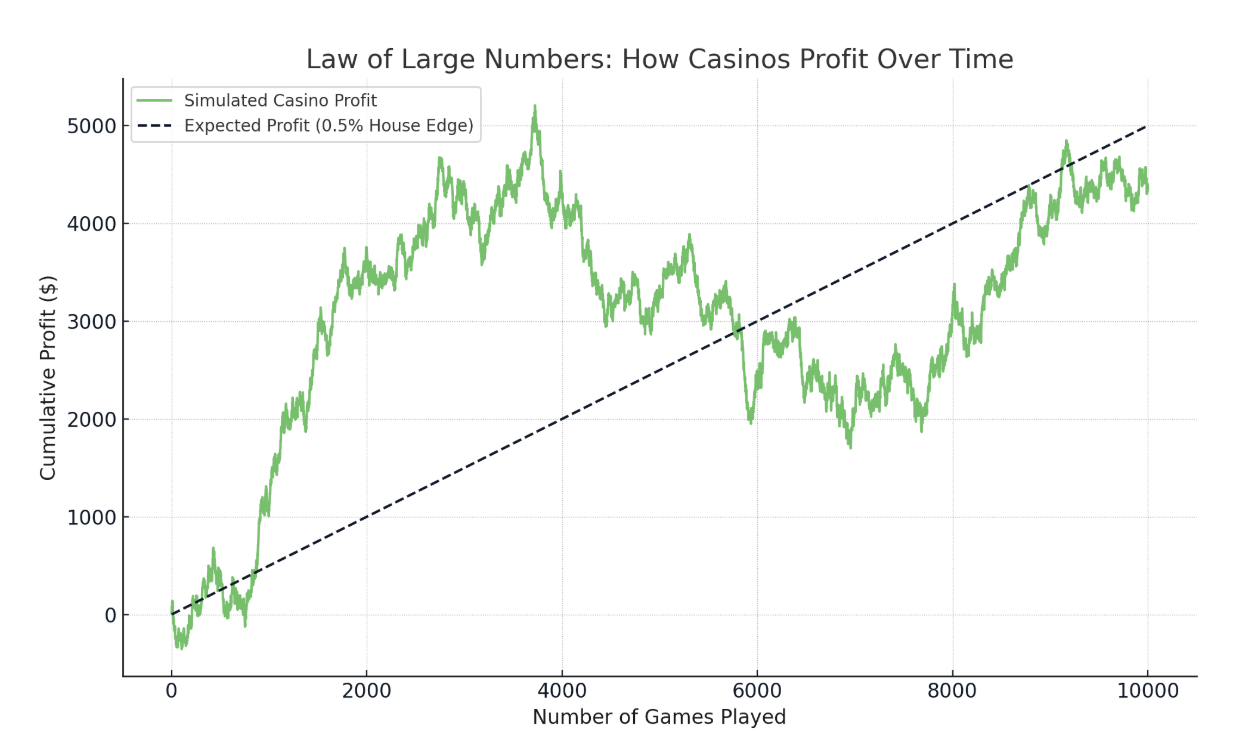
La ventaja del casino gana con más apuestas. Imagen del autor.

Pruebas A/B en empresas tecnológicas

Supón que una empresa quiere probar dos versiones del botón de un sitio web: Botón A y Botón B. Después de que 20 personas prueben cada uno, el Botón A parece mejor. Pero no son datos suficientes para confiar en el resultado.

Ahora deja que 20.000 usuarios vean las dos cosas. A medida que aumenta el tamaño de la muestra, los porcentajes medios de clics se hacen más fiables, y el botón con mejores resultados se hace más evidente.

Por eso las empresas confían en muestras grandes para las pruebas A/B. La ley de los grandes números les ayuda a evitar falsos positivos y a tomar decisiones más inteligentes.

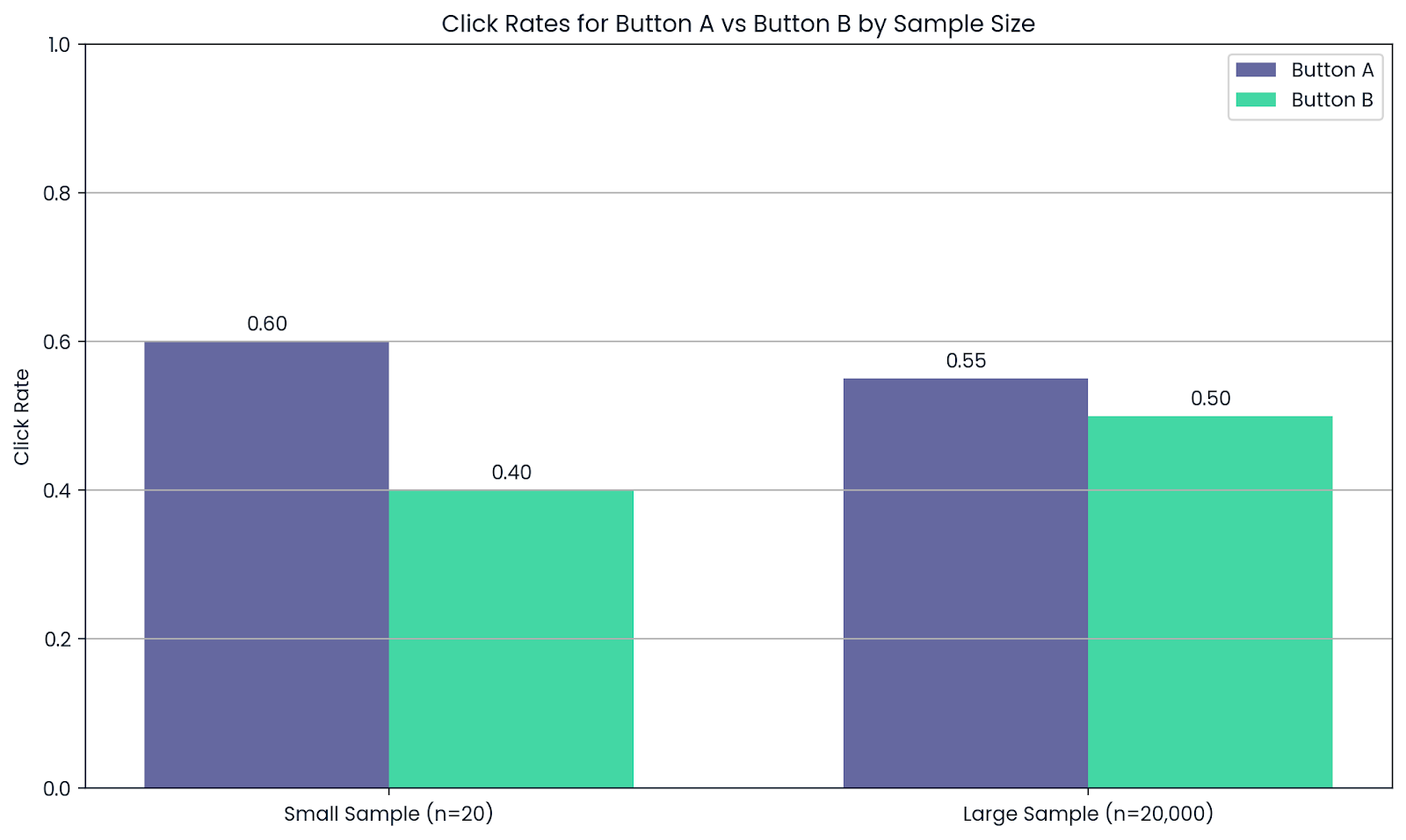
Más personas sometidas a las pruebas significa resultados más fiables. Imagen del autor.

Por qué es importante la Ley de los Grandes Números

En la ciencia de datos, a menudo utilizamos datos para entrenar modelos. Pero si el conjunto de datos es demasiado pequeño, unos pocos valores inusuales pueden sesgar los resultados.

Por ejemplo, estás probando un nuevo algoritmo de recomendación utilizando sólo 10 usuarios. Si un usuario hace clic en todo y otro no hace clic en nada, tu rendimiento medio puede parecer estupendo o terrible. Eso no significa que el modelo sea bueno o malo; significa que tu muestra es demasiado pequeña para confiar en ella.

La ley de los grandes números nos dice que, a medida que recopilamos más datos, las fluctuaciones aleatorias se igualan y el resultado medio se hace más fiable. Por eso los grandes conjuntos de datos proporcionan mejores predicciones y conocimientos.

Esto también se ve en las simulaciones. Por ejemplo, los métodos de Monte Carlo. Consisten en ejecutar el mismo escenario miles de veces utilizando entradas aleatorias. La ley de los grandes números garantiza que cuantos más ensayos hagamos, más se acercará el resultado medio al verdadero resultado esperado.

En el machine learning, la ley aparece de dos formas importantes:

• Formación de modelos: Un modelo entrenado en un conjunto de datos pequeño y desequilibrado puede aprender patrones que no reflejen el mundo real. Pero con suficientes datos diversos, el modelo aprende lo que realmente funciona.
• Prueba de modelos: Probar un modelo con sólo 50 usuarios puede dar resultados muy diferentes a probarlo con 5.000. Un conjunto de pruebas más amplio ofrece una imagen más clara de cómo funcionará el modelo una vez desplegado.

En resumen, más datos significa menos ruido y mejores decisiones. 

Errores comunes

La ley de los grandes números suele malinterpretarse cuando la gente espera que funcione al instante.

Si crees que los resultados se "igualarán" rápidamente, es un error. Por ejemplo, si lanzas una moneda y sale cara cinco veces seguidas, puedes pensar que ahora "toca" cruz para equilibrar las cosas. Pero la probabilidad no funciona así.

Este pensamiento se conoce como falacia del jugador: la falsa idea de que los resultados pasados influyen en los futuros en un proceso verdaderamente aleatorio. En realidad, cada lanzamiento de moneda sigue siendo una probabilidad del 50/50, independientemente de lo que haya ocurrido antes.

La ley de los grandes números no promete que la aleatoriedad se suavice a corto plazo. En cambio, nos dice que a lo largo de muchísimos ensayos, el resultado medio se acerca al valor esperado. En el caso de una moneda justa, eso significa aproximadamente mitad cara y mitad cruz con el tiempo, no inmediatamente.

Aún pueden producirse rachas cortas o patrones inusuales a lo largo del camino. Así es como se ve la aleatoriedad en muestras pequeñas. La ley sólo adquiere sentido cuando te alejas y miras el panorama general.

Cómo se relaciona con otros conceptos

Mientras que la ley de los grandes números nos dice que la media muestral se acerca más a la media real a medida que aumenta el tamaño de la muestra, el teorema del límite central (CLT ) va más allá. Explica cómo es la distribución de esas medias.

Según la CLT, si tomas muchas muestras grandes y calculas sus medias, esas medias formarán una curva en forma de campana (una distribución normal), independientemente de cómo fueran los datos originales. 

Ambas son importantes en estadística, pero describen cosas distintas: una se centra en la precisión, la otra en la forma.

Puntos clave

La ley de los grandes números pone de relieve un principio básico en el análisis de datos: las muestras de mayor tamaño dan resultados más estables y precisos, pero sólo cuando los datos son representativos. 

Aunque los grandes conjuntos de datos reducen los efectos de la variación aleatoria, más datos no siempre son mejores. Si los datos están sesgados o desequilibrados, incluso un conjunto de datos masivo puede producir resultados engañosos. Para sacar conclusiones válidas, necesitas tanto volumen como calidad.

Si quieres construir una base más sólida en estos conceptos, el curso de Pensamiento Estadístico en Python es un buen punto de partida. A partir de ahí, explora la distribución de Gauss para comprender cómo la ley de los grandes números conecta con otras herramientas clave de la estadística y el machine learning.