Équation caractéristique : Tout ce que vous devez savoir sur la science des données

Avec la croissance exponentielle de la disponibilité des données et des techniques d'apprentissage automatique, l'algèbre linéaire a trouvé une place fondamentale dans les mathématiques de l'apprentissage automatique et de la science des données. Ainsi, les aspirants à l'apprentissage automatique et aux scientifiques des données bénéficieront grandement de l'apprentissage des concepts fondamentaux de l'algèbre linéaire, y compris les vecteurs et les matrices, leurs propriétés et les opérations courantes qui leur sont appliquées.

Je vous encourage à suivre notre cours d'algèbre linéaire pour la science des données en R afin de développer une base mathématique solide pour la science des données et l'apprentissage automatique. En suivant ce cours, vous apprendrez à apprécier l'algèbre linéaire comme un sujet magnifique et intéressant qui implique la synthèse de l'algèbre et de la géométrie (à travers les lignes, les plans et les volumes). En particulier, vous verrez comment les données à haute dimension sont bien adaptées pour être représentées sous la forme d'objets vectoriels (par exemple, le texte, les images, l'audio et les caractéristiques), et vous verrez comment ces objets mathématiques en tant que vecteurs ont des applications étendues dans les sciences et l'ingénierie, telles que la physique, les statistiques et l'informatique.

Dans cet article, nous allons examiner de près l'un des objets fondamentaux de l'algèbre linéaire, la matrice. Comme d'autres objets mathématiques, les matrices possèdent certains attributs qui les caractérisent. En particulier, , je passerai en revue et présenterai un attribut caractérisant une matrice carrée : le polynôme caractéristique ou l'équation caractéristique. Jetons un coup d'œil.

Définition de l'équation caractéristique

Un polynôme est une fonction dont les inconnues sont de puissance n. L'inconnue est généralement représentée par la lettre x, mais dans des cas particuliers, une autre notation est utilisée, comme la lettre grecque 𝝀 (lambda), que nous utiliserons dans notre notation. Le polynôme caractéristique d'une matrice carrée A ∈R^n×n et de l'inconnue 𝝀 est défini comme suit :

Où det(.) est le déterminant d'une matrice carrée et I est la matrice identité.

Lorsque nous fixons ce polynôme caractéristique égal à zéro (pour résoudre 𝝀), nous l'appelons l'équation caractéristique. Les racines de cette équation polynomiale sont appelées les valeurs propres, qui sont des concepts importants dans la transformation des matrices et l'apprentissage automatique (par exemple, la réduction de la dimensionnalité). Si vous n'êtes pas sûr des vecteurs propres et des valeurs propres, nous avons un tutoriel sur le sujet : Vecteurs propres et valeurs propres : Les points clés de la science des données.

Dérivation et calcul de l'équation caractéristique

Nous montrons comment un polynôme caractéristique est formulé pour une matrice carrée 2x2 A, où :

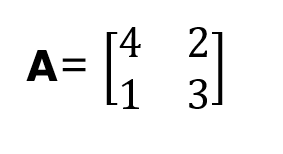
D'après la définition d'un polynôme caractéristique, nous avons :

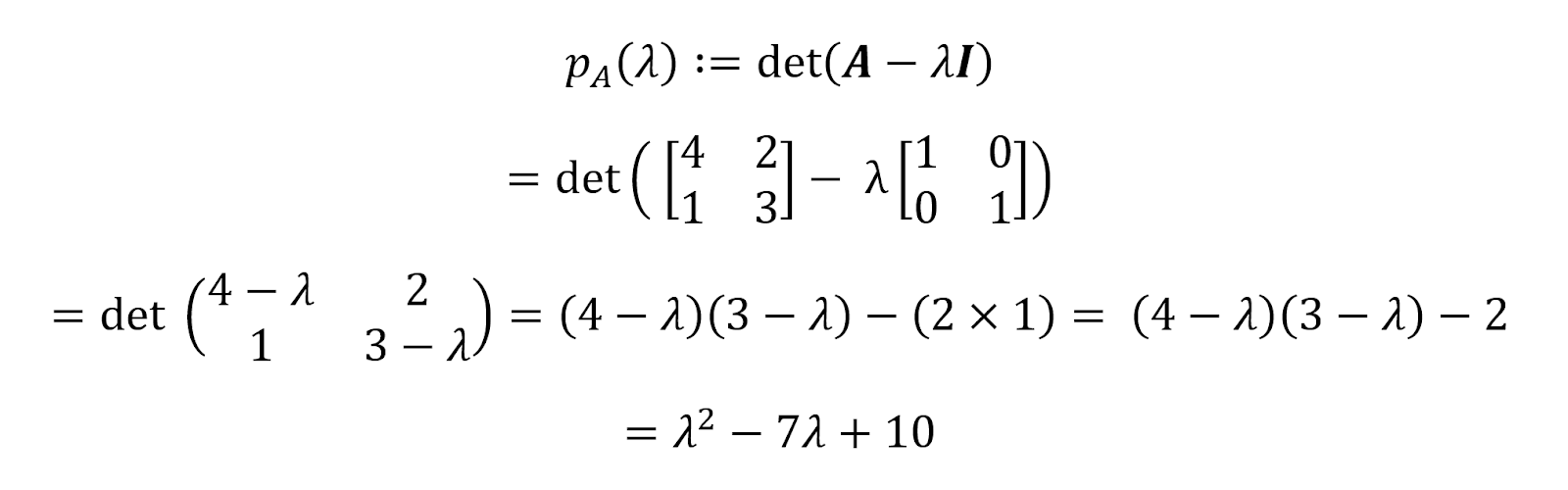
Par conséquent, le polynôme caractéristique de la matrice A ci-dessus est p_A(𝝀)=𝝀2-7𝝀+10. Nous pouvons trouver les racines de ce polynôme en le mettant en équation avec zéro.

Utilisation de l'équation caractéristique pour trouver les valeurs propres et les vecteurs propres

Le polynôme caractéristique d'une matrice carrée contient des caractéristiques importantes sur la matrice associée, notamment les valeurs propres et le déterminant. Il est donc possible d'extraire les valeurs propres d'un polynôme caractéristique en résolvant l'inconnue. Nous avons illustré ci-dessus le processus de recherche des valeurs propres à partir du polynôme caractéristique d'une matrice carrée A 2x2. Comme nous l'avons montré, le polynôme caractéristique de cette matrice est :

Maintenant, pour trouver les valeurs propres, nous mettons ce polynôme en équation avec zéro et trouvons les racines à l'aide de méthodes algébriques (ou informatiques) :

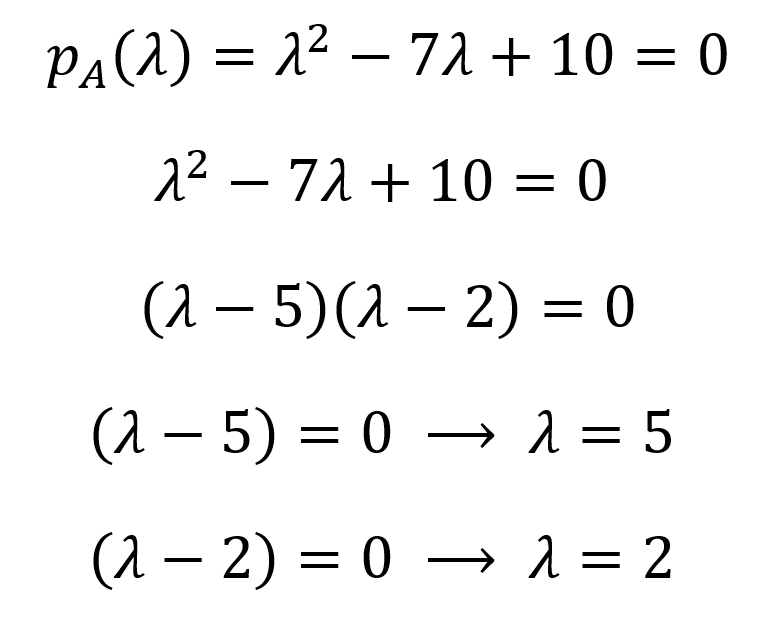
Les valeurs propres sont donc 𝝀₁=5 et 𝝀₂=2 (les valeurs propres sont conventionnellement classées par ordre décroissant, car elles impliquent la quantité d'informations dans certaines matrices de données). L'ensemble des valeurs propres d'une matrice est appelé spectre propre ou spectre de cette matrice. À partir des valeurs propres, on peut dériver les vecteurs propres d'une matrice dans l'espace nul en utilisant (A-𝝀I)x=0 pour chaque valeur propre :

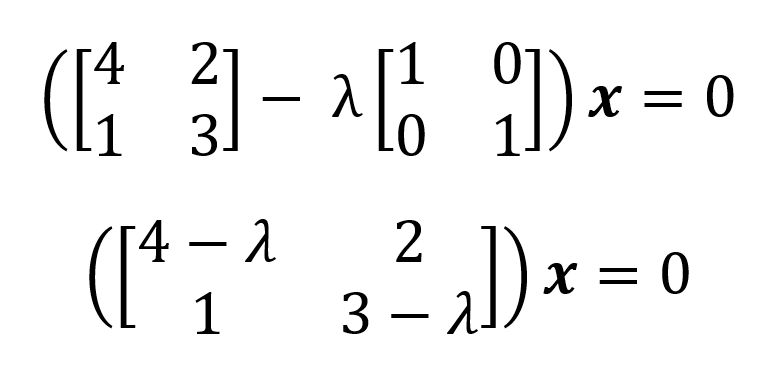
Pour𝝀₁=5 nous introduisons 5 et résolvons le système d'équations homogènes :

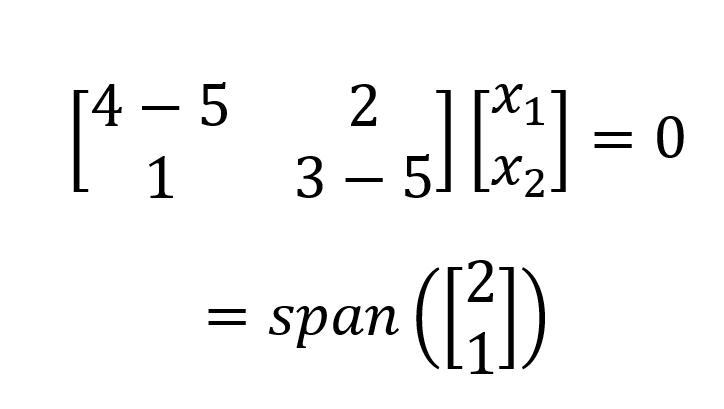
Ce qui donne un espace propre unidimensionnel (c'est-à-dire un vecteur de base). Nous procédons de la même manière pour 𝝀₂=2 et obtenons :

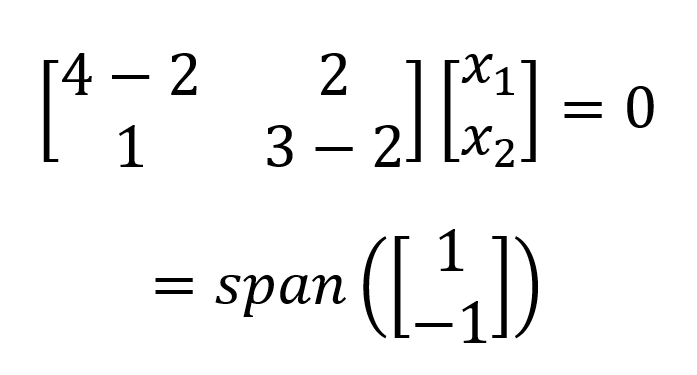
Dans cet exemple, nous avons deux valeurs propres distinctes. Une matrice peut également avoir plusieurs valeurs propres identiques répétées, ce qui donne un espace propre multidimensionnel (c'est-à-dire plusieurs vecteurs de base). Dans ce cas, la dimension de l'espace propre couvert par des vecteurs propres distincts est appelée multiplicité géométrique de la valeur propre i.

En revanche, le nombre de fois qu'une valeur propre d'une matrice est répétée est appelé multiplicité algébrique. L'une des applications les plus intéressantes des valeurs propres et des vecteurs propres est probablement l'algorithme PageRank que Google utilise pour classer les résultats de recherche par ordre d'importance. Notre cours Predictive Analytics using Networked Data in R contient un chapitre intéressant sur l'algorithme PageRank si vous êtes intéressé. 

Techniques de calcul

Un polynôme caractéristique est en fait un polynôme mathématique doté de propriétés particulières (par exemple, il comprend la trace, le déterminant et les valeurs propres d'une matrice carrée). Ainsi, la recherche des racines de l'équation caractéristique devient fastidieuse lorsque le nombre de degrés n augmente. 

En outre, pour obtenir le polynôme caractéristique, vous devez calculer le déterminant de la matrice carrée. Bien que, pour des raisons pédagogiques, nous ayons fourni un exemple et une méthode pour dériver et résoudre le polynôme caractéristique sur papier et à la main, dans les applications réelles de la science des données, des méthodes numériques (informatiques) sont utilisées pour calculer ou approximer les racines d'un polynôme caractéristique. L'expansion de Laplace, l'élimination gaussienne et les décompositions QR sont des méthodes qui permettent de trouver numériquement les déterminants. 

Pour trouver les racines du polynôme caractéristique, les algorithmes courants comprennent la méthode de Newton-Raphson, la bissection, la méthode de la sécante et la méthode de Muller.

Applications de l'équation caractéristique

Les valeurs propres et les vecteurs propres sont des caractéristiques mathématiques fondamentales des matrices qui peuvent être dérivées de l'équation caractéristique d'une matrice carrée. En statistique et en apprentissage automatique, les équations caractéristiques sont utilisées pour différents algorithmes basés sur les valeurs propres et utilisés pour la réduction des données et les algorithmes d'extraction d'informations, comme par exemple :

• l'analyse en composantes principales (ACP) et la réduction de la dimensionnalité, où un ensemble de données est réduit à un plus petit nombre de vecteurs sur la base des valeurs propres extraites.
• Regroupement spectralIl s'agit d'une technique basée sur le spectre propre de la matrice de similarité d'un ensemble de données afin de réduire la dimensionnalité des données avant d'exécuter des algorithmes de regroupement, tels que le regroupement par k-moyennes.
• Théorie des graphes et l'analyse des réseaux, où les valeurs propres et les vecteurs propres sont utilisés pour diviser un graphe en communautés (composantes principales), en intégrant le graphe dans un espace de dimension inférieure pour la visualisation, et la sparsification spectrale pour approximer un graphe avec un spectre propre similaire.
• Séries temporellesL'analyse du spectre singulier est utilisée pour découvrir les modèles sous-jacents de la série, tels que les tendances, les cycles et les anomalies.

Propriétés du polynôme caractéristique

En tant qu'objet mathématique, un polynôme caractéristique possède certaines propriétés intéressantes, notamment

• Monic: Le premier coefficient d'un polynôme caractéristique est toujours égal à un (monique).
• Diplôme: Le degré n d'un polynôme caractéristique est toujours égal à la taille de lamatrice nx n associée.
• Invariance sous similitude matricielle: Si nous transformons une matrice et que le résultat est une matrice similaire, elles ont toutes deux un polynôme caractéristique identique (c'est-à-dire que la matrice similaire transformée conserve le polynôme caractéristique d'origine).
• Coefficients: Le premier terme du polynôme caractéristique est le déterminant de la matrice associée, et l'avant-dernier coefficient est la trace non signée de la matrice associée c₀=det(A) et c_n-1=-1^n-1tr(A)
• Dans le polynôme caractéristique, si nous remplaçons chaque inconnue par la matrice carrée originale, le résultat sera une matrice nulle (théorème de Cayley-Hamilton). En d'autres termes, le polynôme caractéristique est un polynôme annihilant pour la matrice carrée. Sous cette forme, les valeurs propres peuvent être directement dérivées de la matrice carrée. En conséquence, on peut affirmer que chaque matrice carrée satisfait à sa propre équation caractéristique.

Sujets avancés

Enfin, j'aimerais donner quelques détails plus avancés concernant les polynômes caractéristiques et les propriétés des matrices pour approfondir les mathématiques, mais sans entrer dans les détails.

• Polynôme minimal: Un polynôme monique étroitement lié au polynôme caractéristique est le polynôme minimal, qui est un polynôme du plus petit degré positif qui annihile la matrice carrée A. Étant donné qu'un polynôme caractéristique peut également annihiler sa matrice carrée, le polynôme minimal peut être dérivé de ce polynôme caractéristique.
• Similitude et diagonalisation: Deux matrices sont similaires si elles sont liées l'une à l'autre par une transformation linéaire commune. Si deux matrices sont similaires, elles ont également le même rang, la même trace, le même déterminant, les mêmes valeurs propres, le même polynôme caractéristique et les mêmes polynômes minimaux. 
• Equation caractéristique des puissances et fonctions matricielles: Dans une puissance matricielle, les valeurs propres sont élevées à la puissance k de la matrice^Ak et le polynôme caractéristique correspondant est dérivé comme det(A^k-λI). Pour une fonction matricielle f(x), le polynôme caractéristique peut être dérivé en évaluant f() aux valeurs propres de A.

Conclusion

Dans cet article, nous avons appris à connaître le polynôme caractéristique et la façon dont il contient des propriétés importantes d'une matrice carrée, telles que les valeurs propres, la trace et le déterminant. Étant donné le rôle important des valeurs propres dans la science des données et l'apprentissage automatique, la compréhension de l'équation caractéristique nous aide grandement à comprendre comment les algorithmes statistiques et d'apprentissage automatique extraient les principaux composants d'une matrice de données afin de trouver des modèles et d'améliorer l'efficacité des calculs.

Si vous souhaitez en savoir plus sur d'autres équations importantes et bien connues dans le domaine de la science des données et de l'apprentissage automatique, consultez notre tutoriel sur l'équation normale pour la régression linéaire. DataCamp propose également d'excellents cours pour un parcours d'apprentissage complet et structuré, comme notre cours Linear Algebra for Data Science in R, que j'ai mentionné plus tôt et que je recommande absolument.