Characteristic Equation: Everything You Need to Know for Data Science

With the exponential growth in availability of data and machine learning techniques, linear algebra has found a fundamental place in the mathematics of machine learning and data science. As such, aspiring machine learning and data scientists will greatly benefit from learning fundamental concepts in linear algebra, including vectors and matrices, their properties, and common operations applied to them.

I encourage you to take our Linear Algebra for Data Science in R course to develop a strong mathematical foundation for data science and machine learning. By taking the course, you will come to appreciate linear algebra as a beautiful and interesting subject that involves the synthesis of algebra and geometry (through lines, planes, and volumes). In particular, you will see how high-dimensional data are well-suited to be represented in the form of vector objects (e.g., text, images, audio, and features), and you will see how these mathematical objects as vectors have extensive applications in science and engineering, such as physics, statistics, and computer science.

In this article, we will look closely at one of the fundamental objects in linear algebra called a matrix. Like other mathematical objects, matrices have some attributes that characterize them. In particular, I will review and present one characterizing attribute of a square matrix: the characteristic polynomial or characteristic equation. Let's take a look.

Definition of the Characteristic Equation

A polynomial is a function with unknowns of power n. The unknown is generally shown by the letter x, but in special use cases, a different notation is used, such as the Greek letter 𝝀 (lambda), which we will use in our notation. The characteristic polynomial of a square matrix A ∈R^n×n and the unknown 𝝀 is defined as:

Where det(.) is the determinant of a square matrix and I is the identity matrix. 

When we set this characteristic polynomial equal to zero (to solve for 𝝀), we call it the characteristic equation. The roots of this polynomial equation are called the eigenvalues, which are important concepts in matrix transformation and machine learning (e.g., dimensionality reduction). If you are unsure about eigenvectors and eigenvalues, we have a tutorial on the subject: Eigenvectors and Eigenvalues: Key Insights for Data Science.

Deriving and Computing the Characteristic Equation

We show how a characteristic polynomial is formulated for a 2x2 square matrix A, where:

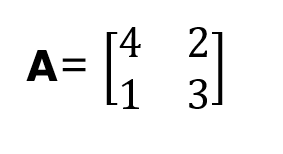
From the definition of a characteristic polynomial, we have:

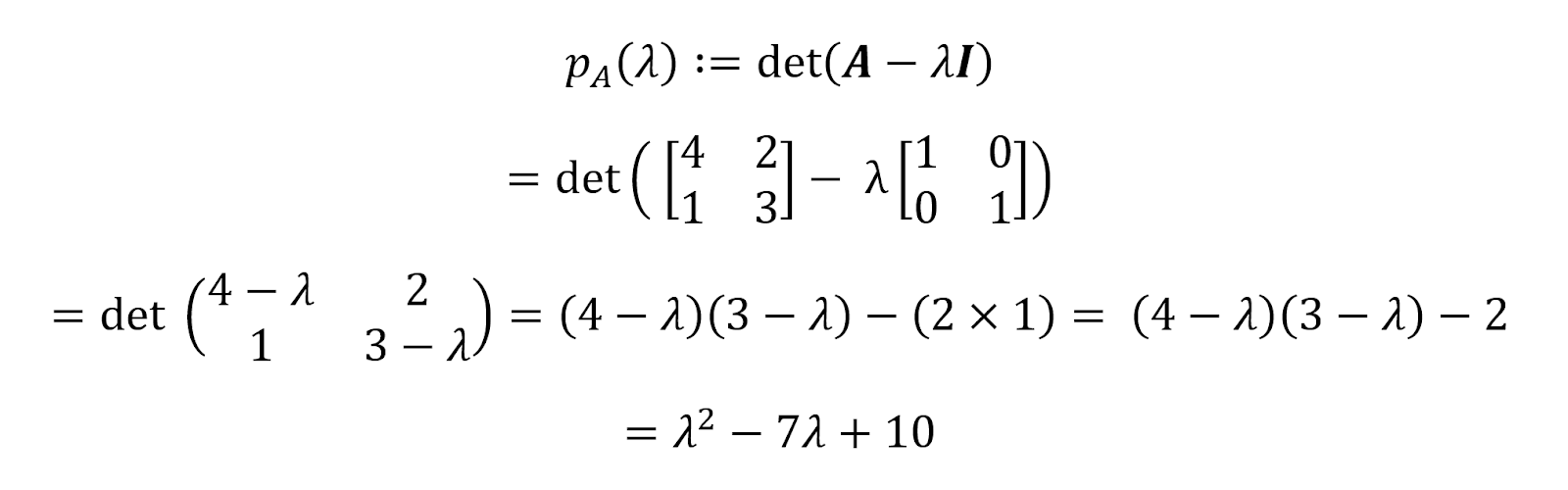
Therefore, the characteristic polynomial for the matrix A above is p_A(𝝀)=𝝀²-7𝝀+10. We can find the roots of this polynomial by equating it to zero.

Using the Characteristic Equation to Find Eigenvalues and Eigenvectors

A characteristic polynomial of a square matrix contains important characteristics about its associated matrix, including the eigenvalues and the determinant. Therefore, it is possible to extract eigenvalues from a characteristic polynomial by solving for the unknown. We illustrate the process of finding eigenvalues from the characteristic polynomial for a 2x2 square matrix A above. As we showed, the characteristic polynomial for this matrix is:

Now, to find the eigenvalue(s), we equate this polynomial to zero and find the roots using algebraic (or computational) methods:

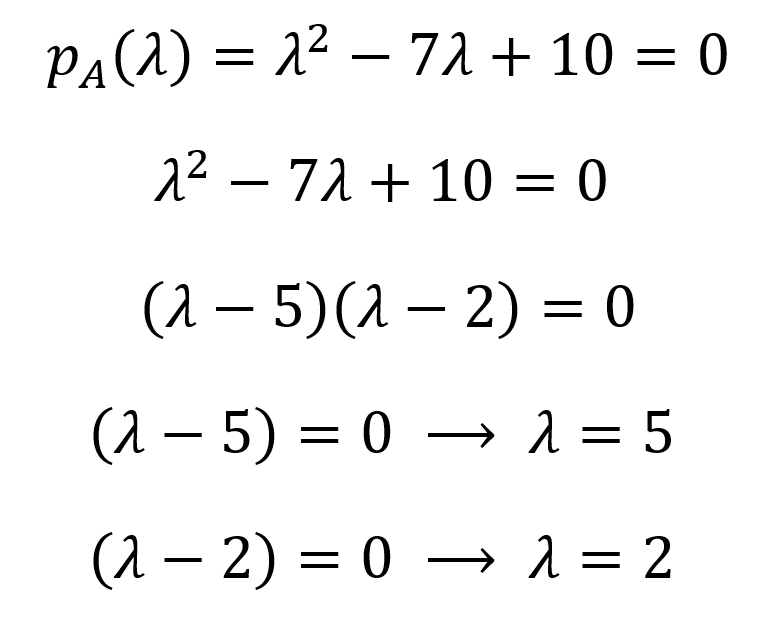
So, the eigenvalues are 𝝀₁=5 and 𝝀₂=2 (eigenvalues are conventionally listed in decreasing order, as they imply the amount of information in certain data matrices). The set of all eigenvalues of a matrix is called the eigenspectrum or the spectrum of that matrix. From eigenvalues, we can derive the eigenvectors of a matrix in the null space using (A-𝝀I)x=0 for each eigenvalue:

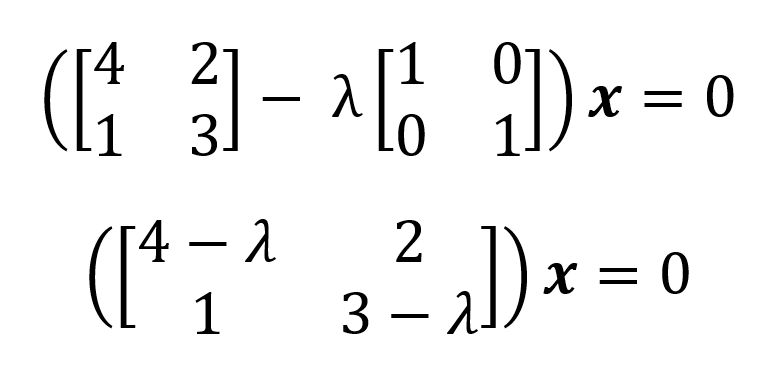
For𝝀₁=5 we plug in 5 and solve the homogeneous system of equations:

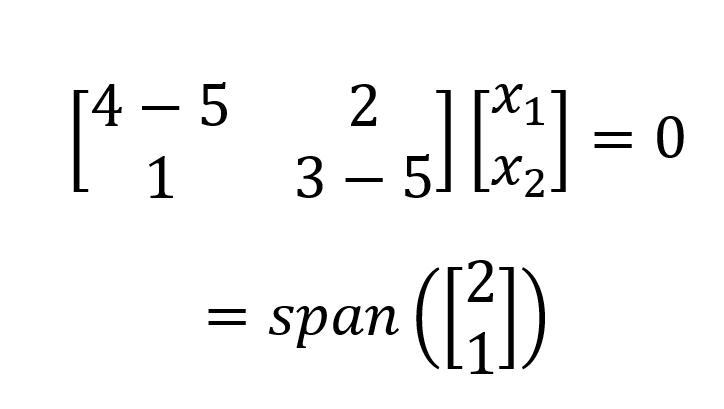
Which gives a one-dimensional (i.e., one basis vector) eigenspace. We perform the same process for 𝝀₂=2 and get:

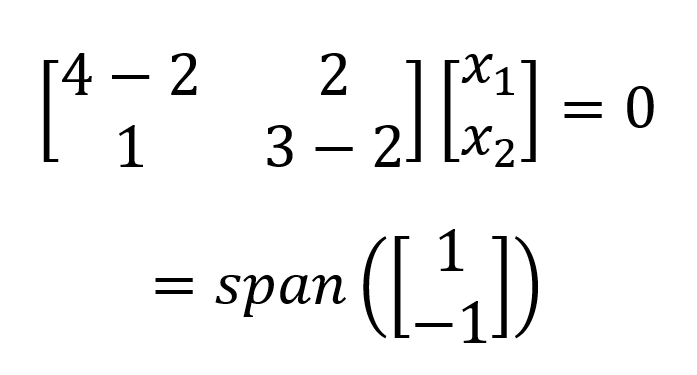
In this example, we have two distinct eigenvalues. A matrix may also have several repeated identical eigenvalues, giving a multidimensional (i.e., several basis vectors) eigenspace. In this case, the dimensionality of the eigenspace spanned by distinct eigenvectors is called the geometric multiplicity of the eigenvalue i. 

On the other hand, the number of times an eigenvalue of a matrix is repeated is called the algebraic multiplicity. Probably, one of the most interesting applications of eigenvalues and eigenvectors is the PageRank algorithm that Google uses for the importance ranking of search results. Our Predictive Analytics using Networked Data in R course has an interesting chapter on the PageRank algorithm if you are interested. 

Computational Techniques

A characteristic polynomial is, in fact, a mathematical polynomial with special properties (e.g., it includes the trace, the determinant, and the eigenvalues of a square matrix). As such, finding the roots of the characteristic equation becomes cumbersome with higher degrees of n. 

In addition, deriving the characteristic polynomial requires you to compute the determinant of the square matrix. Although for pedagogical reasons, we provided an example and method to derive and solve the characteristic polynomial on paper and by hand, in real data science applications, numerical (computational) methods are used to compute or approximate the roots of a characteristic polynomial. Laplace expansion, Gaussian elimination, and QR decompositions are some methods that can numerically find the determinants. 

For finding the roots of the characteristic polynomial, common algorithms include Newton-Raphson’s method, bisection, secant method, and Muller’s method.

Applications of the Characteristic Equation

Eigenvalues and eigenvectors are fundamental mathematical characteristics of matrices that can be derived from a characteristic equation of a square matrix. In statistics and machine learning, characteristic equations are used for different algorithms that are based on eigenvalues and which are used for data reduction and information extraction algorithms, such as:

• Principal Component Analysis (PCA) and dimensionality reduction, where a dataset is reduced to a smaller number of vectors based on the values of the extracted eigenvalues.
• Spectral Clustering, which is a technique based on the eigenspectrum of the similarity matrix of a dataset to reduce data dimensionality as a step before running clustering algorithms, such as k-means clustering.
• Graph Theory and network analysis, where eigenvalues and eigenvectors are used to partition a graph into communities (main components), embedding the graph into a lower dimensional space for visualization, and spectral sparsification to approximate a graph with similar eigenspectrum.
• Time series, where singular spectrum analysis is used to discover underlying patterns in the series, such as trends, cycles, and anomalies.

Properties of the Characteristic Polynomial

As a mathematical object, a characteristic polynomial has some interesting properties, including:

• Monic: The leading coefficient of a characteristic polynomial is always one (monic).
• Degree: The degree n of a characteristic polynomial is always equal to the size of the associated nxn matrix.
• Invariance Under Matrix Similarity: If we transform a matrix and the result is a similar matrix, they both have an identical characteristic polynomial (i.e., the transformed similar matrix retains the original characteristic polynomial).
• Coefficients: The first leading term of the characteristic polynomial is the determinant of the associated matrix, and the last but second coefficient is the unsigned trace of the associated matrix c₀=det(A) and c_n-1=-1^n-1tr(A)
• In the characteristic polynomial, if we replace each unknown with the original square matrix, the result will be a zero matrix (Cayley-Hamilton Theorem). In other words, the characteristic polynomial is an annihilating polynomial for the square matrix. In this form, the eigenvalues can be directly derived from the square matrix. Accordingly, it can be stated that every square matrix satisfies its own characteristic equation.

Advanced Topics

Finally, I want to offer a few more advanced details related to characteristic polynomials and matrix properties as a further look into the math, but without extensive detail.

• Minimal Polynomial: A monic polynomial closely related to characteristic polynomial is the minimal polynomial, which is a polynomial of least degree positive that annihilates the square matrix A. Because a characteristic polynomial can also annihilate its square matrix, the minimal polynomial can be derived from such characteristic polynomial.
• Similarity and Diagonalization: Two matrices are similar if they are related to each other through one common linear transformation. If two matrices are similar, then they also have the same rank, trace, determinant, eigenvalues, characteristic polynomial, and minimal polynomials. 
• Characteristic Equation of Matrix Powers and Functions: In a matrix power, the eigenvalues are raised to the kth power of the matrix A^k and the corresponding characteristic polynomial is derived as det(A^k-λI). For a matrix function f(x), the characteristic polynomial can be derived by evaluating f() at the eigenvalues of A.

Conclusion

In this article, we learned about the characteristic polynomial and the ways it contains important properties of a square matrix, such as the eigenvalues, the trace, and the determinant. Given the important role of eigenvalues in data science and machine learning, comprehension of the characteristic equation greatly helps us in understanding how machine learning and statistical algorithms extract the main components from a data matrix to find patterns and improve computing efficiency.

If you are interested in reading up on other important and well-known equations in data science and machine learning, check out our Normal Equation for Linear Regression Tutorial. DataCamp also has great courses for a comprehensive and structured learning path, such as our Linear Algebra for Data Science in R course, which I mentioned earlier and definitely recommend.