Matrice singulière : Concepts clés et exemples en science des données

Une matrice singulière est une matrice carrée qui ne peut pas être inversée, ce qui signifie qu'elle n'a pas d'inverse multiplicatif. Ce concept fondamental de l'algèbre linéaire a un impact considérable sur les applications de la science des données, depuis les algorithmes d'apprentissage automatique jusqu'à la stabilité numérique dans les méthodes de calcul.

Dans cet article, nous allons définir ce qui rend une matrice singulière et explorer ses propriétés et caractéristiques mathématiques. Nous examinerons ensuite les méthodes de détection des matrices singulières. Nous comprendrons leurs implications réelles dans la science des données et nous apprendrons à les gérer efficacement.

Qu'est-ce qu'une matrice singulière ?

Une matrice singulière est une matrice carrée dont le déterminant est égal à zéro, ce qui la rend non inversable. 

En termes mathématiques, pour une matrice carrée A, si det(A) = 0, alors A est singulière et n'a pas de matrice inverse A-¹.

La caractéristique fondamentale d'une matrice singulière est que ses lignes ou ses colonnes sont linéairement dépendantes, ce qui signifie qu'au moins une ligne (ou une colonne) peut être exprimée comme une combinaison linéaire des autres lignes (ou colonnes). Cette dépendance crée une "lacune" dans la matrice qui l'empêche d'avoir un inverse unique.

Une autre façon de comprendre les matrices singulières est de s'intéresser à leur rang. Une matrice carrée est singulière si et seulement si son rang est inférieur à son nombre de lignes (ou de colonnes). Le rang représente le nombre maximal de lignes ou de colonnes linéairement indépendantes, de sorte que lorsqu'il est inférieur aux dimensions de la matrice, il y a singularité.

Ce concept est important car de nombreux algorithmes reposent sur l'inversion de matrices, qu'il s'agisse de résoudre des problèmes de régression linéaire ou de mettre en œuvre certaines techniques d'apprentissage automatique. Lorsqu'une matrice est singulière, ces opérations échouent, ce qui nécessite d'autres approches ou étapes de prétraitement pour gérer la situation.

Propriétés et conditions des matrices singulières

Comprendre les propriétés mathématiques des matrices singulières permet d'identifier les problèmes potentiels avant qu'ils n'entraînent des problèmes de calcul dans les flux de travail de la science des données.

• Déterminant zéro: Le déterminant d'une matrice singulière est toujours égal à zéro, ce qui indique directement la non-invertibilité. Ce déterminant nul signifie que la transformation de la matrice n'est pas bijective, ce qui permet à plusieurs vecteurs d'entrée de correspondre à la même sortie.
• Dépendance linéaire: Les matrices singulières contiennent des lignes ou des colonnes linéairement dépendantes, où au moins une ligne peut être exprimée comme une combinaison linéaire des autres. Cette dépendance crée des informations redondantes qui posent des problèmes de calcul.
• Déficience de rang: Une matrice n×n singulière a un rang inférieur à n et possède moins de lignes ou de colonnes linéairement indépendantes que sa dimension. Cette lacune explique pourquoi les systèmes impliquant des matrices singulières n'ont pas de solutions uniques.
• Valeurs propres nulles: Au moins une valeur propre d'une matrice singulière est exactement nulle, ce qui correspond aux directions de l'espace qui sont complètement écrasées lors de la transformation. Le nombre de valeurs propres nulles est égal à la nullité de la matrice.
• Espace nul non trivial: Les matrices singulières ont des vecteurs non nuls qui, lorsqu'ils sont multipliés par la matrice, produisent le vecteur zéro. La dimension de cet espace nul indique la quantité d'informations perdues au cours de la transformation.

Maintenant que nous avons compris les propriétés fondamentales d'une matrice singulière, opposons-les aux matrices non singulières.

Singulier vs. Matrice non singulière

Les matrices non singulières sont inversibles et permettent des calculs numériques fiables, tandis que les matrices singulières n'ont pas d'inverses et nécessitent un traitement spécialisé. Ce clivage fondamental détermine la faisabilité informatique des applications de la science des données. 

Ces différences s'appliquent à chacune des propriétés fondamentales d'une matrice singulière que nous avons vues précédemment. Le tableau ci-dessous résume les différences entre les matrices singulières et non singulières :

Exemples de matrices singulières

L'examen d'exemples spécifiques permet d'illustrer la manière dont la singularité se manifeste dans la pratique et de développer une intuition pour reconnaître ces matrices.

Matrice singulière simple 2×2

Considérez cet exemple de base où une ligne est un multiple d'une autre :

Matrice singulière simple 2×2 (Image de l'auteur)

Ici, la deuxième ligne est exactement la moitié de la première, ce qui crée une dépendance linéaire. Le déterminant est (2×2) - (4×1) = 0, ce qui confirme la singularité.

Ligne ou colonne zéro

Toute matrice contenant une ligne ou une colonne de zéros est automatiquement singulière :

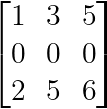
Ligne ou colonne zéro (Image de l'auteur)

La ligne zéro empêche la matrice d'avoir un rang complet, quelles que soient les autres entrées.

Lignes ou colonnes identiques

Les matrices dont les lignes ou les colonnes sont identiques sont toujours singulières :

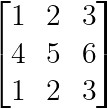
Lignes ou colonnes identiques (Image de l'auteur)

Les première et troisième lignes sont identiques, ce qui crée une dépendance linéaire parfaite.

Combinaison linéaire dépendance

Une singularité plus subtile se produit lorsqu'une rangée est égale à une combinaison d'autres rangées :

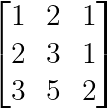
Combinaison linéaire dépendance (Image de l'auteur)

Ici, la troisième ligne est égale à la somme des deux premières : [3,5,2] = [1,2,1] + [2,3,1].

Chacun des exemples ci-dessus montre comment des matrices apparemment différentes peuvent partager la propriété fondamentale de dépendance linéaire qui définit la singularité.

Pourquoi les matrices singulières apparaissent-elles dans la science des données ?

Les matrices singulières apparaissent fréquemment dans les applications de science des données en raison de la nature des données du monde réel et des flux de travail analytiques courants.

Multicollinéarité dans les ensembles de caractéristiques

La source la plus courante de matrices singulières en science des données est la multicolinéarité, lorsque plusieurs caractéristiques d'un ensemble de données sont parfaitement ou presque parfaitement corrélées. Cela crée une dépendance linéaire entre les colonnes de la matrice de conception, ce qui entraîne une singularité lors des opérations matricielles.

Prenons l'exemple d'un ensemble de données de vente au détail pour lequel vous disposez de caractéristiques pour total_sales, q1_sales, q2_sales, q3_sales et q4_sales. Si les valeurs des ventes trimestrielles correspondent toujours exactement aux ventes totales, alors.. :

total_sales = q1_sales + q2_sales + q3_sales + q4_sales

Lorsque cette relation se vérifie parfaitement pour toutes les observations, la matrice de conception résultante devient singulière. Tout algorithme de régression linéaire tentant d'inverser cette matrice échouera car une colonne peut être parfaitement prédite à partir des autres.

Des scénarios similaires se produisent avec des caractéristiques dérivées telles que

• Température en Celsius et Fahrenheit
• Âge et année de naissance (pour une année de référence fixe)
• Ratios dont le numérateur et le dénominateur sont également des caractéristiques
• Variables fictives dont la somme est égale à une constante (piège des variables fictives)

Données insuffisantes concernant les caractéristiques

Les ensembles de données à haute dimension comportant moins d'observations que de caractéristiques produisent naturellement des matrices singulières. Lorsque vous avez n échantillons mais p caractéristiques où p > n, la matrice de covariance n×n ou la matrice de gramme résultante aura un rang au plus égal à n, ce qui la rend singulière si vous avez besoin d'une matrice inversible p×p.

Cette "malédiction de la dimensionnalité" affecte généralement :

• Données génomiques avec des milliers de gènes mais des centaines d'échantillons
• Analyse de texte avec de grands vocabulaires mais des documents limités
• Traitement d'images avec des caractéristiques à haute résolution mais de petits ensembles d'apprentissage
• Modélisation financière avec de nombreux indicateurs économiques, mais des séries chronologiques courtes

Prétraitement des données 

Les étapes courantes de prétraitement des données peuvent introduire par inadvertance une singularité :

• Centrer les transformations: Le centrage de chaque caractéristique (soustraction de la moyenne) n'entraîne pas de singularité en soi, mais en présence d'autres dépendances linéaires, il peut les préserver ou les accentuer. Dans les cas où les caractéristiques sont déjà presque dépendantes, le centrage peut les rapprocher d'une dépendance exacte avec une précision limitée.
• Mise à l'échelle et normalisation: Certaines opérations de mise à l'échelle peuvent accentuer des relations linéaires subtiles, poussant des caractéristiques presque dépendantes à une dépendance parfaite en raison des limites de précision de la virgule flottante.
• Ingénierie des fonctionnalités: La création de caractéristiques polynomiales, de termes d'interaction ou d'expansions de base peut introduire des relations linéaires inattendues. Par exemple, si vous créez les caractéristiques x, ^x² et ^2x²- x, la troisième caractéristique(^2x²- x) est parfaitement déterminée par les deux premières.

La compréhension de ces sources communes de singularité permet aux scientifiques des données de mettre en œuvre des mesures préventives dès le début de leur travail, comme la vérification de la multicollinéarité lors de l'analyse exploratoire des données ou l'utilisation de techniques de régularisation de manière proactive.

Maintenant que nous comprenons pourquoi les matrices singulières apparaissent dans la science des données, explorons les méthodes pratiques pour les détecter avant qu'elles ne provoquent des pannes de calcul.

Comment détecter les matrices singulières

La façon la plus simple de détecter une matrice singulière est de vérifier son déterminant. Si le déterminant d'une matrice carrée est zéro, la matrice est singulière et non inversable. Cette méthode est simple, mathématiquement solide et largement utilisée dans la pratique.

Comprenons comment effectuer cette vérification à l'aide de Python :

import numpy as np

# Example 2x2 matrix
A = np.array([[2, 4],
             [1, 2]])

# Calculate the determinant
det_A = np.linalg.det(A)

print(f"Determinant of A: {det_A}")

# Check if matrix is singular
if np.isclose(det_A, 0):
   print("Matrix A is singular.")
else:
   print("Matrix A is non-singular.")

Dans l'exemple ci-dessus, nous définissons une matrice A2×2 et utilisons np.linalg.det() pour calculer son déterminant. Comme l'arithmétique en virgule flottante peut introduire de petites erreurs numériques, nous utilisons np.isclose() pour vérifier si le déterminant est effectivement nul. Si c'est le cas, nous concluons que la matrice est singulière. 

Nous verrons ci-dessous le résultat confirmant la singularité :

Matrice singulière de détection de sortie. (Image de l'auteur)

Cette méthode est à la fois intuitive et pratique, ce qui en fait une première étape fiable pour diagnostiquer les problèmes liés à l'inversibilité des matrices dans les flux de travail de la science des données.

Comment traiter les matrices singulières en pratique

Lorsque des matrices singulières sont rencontrées dans les flux de travail de la science des données, plusieurs stratégies permettent de résoudre les problèmes de calcul tout en préservant l'intégrité analytique.

Techniques de régularisation

L'ajout de petites valeurs à la diagonale (régularisation Ridge) est l'approche la plus courante pour traiter les matrices quasi-singulaires dans les problèmes de régression. Cette technique transforme les matrices singulières en matrices inversibles tout en maintenant la stabilité numérique :

# Ridge regularization approach
lambda_reg = 1e-6
A_regularized = A + lambda_reg * np.eye(A.shape[0])

Calcul de la pseudo-inverse

La pseudo-inverse de Moore-Penrose fournit une inverse généralisée pour les matrices singulières, offrant la "meilleure" solution au sens des moindres carrés :

# Using pseudoinverse for singular matrices
A_pinv = np.linalg.pinv(A)
x = A_pinv @ b 

Réduction de la dimensionnalité

La suppression des caractéristiques linéairement dépendantes permet d'éliminer la singularité à sasource. L'analyse des composantes principales ou lestechniques de sélection des caractéristiques permettent d'identifier et de supprimer les dimensions redondantes :

# PCA-based dimensionality reduction
from sklearn.decomposition import PCA
pca = PCA(n_components=0.95) 
X_reduced = pca.fit_transform(X)

Algorithmes alternatifs

Certains algorithmes sont spécifiquement conçus pour traiter les matrices singulières. La décomposition QR avec pivotement permet de résoudre des systèmes linéaires même lorsque la matrice des coefficients est singulière, en fournissant des solutions lorsqu'elles existent et en identifiant les incohérences lorsqu'elles n'existent pas.

Ces stratégies permettent de s'assurer que les matrices singulières ne font pas dérailler les projets de science des données tout en maintenant la rigueur mathématique et l'interprétabilité des résultats.

Conclusion

Cet article a exploré les matrices singulières, dont nous avons appris qu'il s'agit de matrices carrées à déterminant nul qui ne peuvent être inversées en raison de dépendances linéaires entre les lignes ou les colonnes. Nous avons examiné les raisons pour lesquelles ils apparaissent fréquemment dans la science des données, de la multicolinéarité et des données de haute dimension aux problèmes introduits lors du prétraitement. 

Dans cet article, nous avons également passé en revue les moyens de détecter et de traiter les matrices singulières à l'aide de techniques de base telles que la vérification des déterminants, la régularisation, les pseudo-inverses et la réduction de la dimensionnalité. (Si vous souhaitez aller plus loin par vous-même, des outils tels que l'analyse des nombres de conditions ou la décomposition en valeurs singulières peuvent vous permettre de mieux comprendre le comportement des matrices et la stabilité numérique).

Pour approfondir votre compréhension de l'algèbre linéaire et de son rôle essentiel dans les applications de science des données, inscrivez-vous à notre cours d' algèbre linéaire pour la science des données, où vous maîtriserez ces concepts fondamentaux et leurs implémentations dans des scénarios du monde réel.