Regroupement hiérarchique : Aperçu du concept avec exemples

On vient de vous confier l'analyse d'un vaste ensemble de données et on vous demande de fournir une analyse approfondie des grappes. Vous avez déjà rencontré le terme "clustering hiérarchique", mais de quoi s'agit-il exactement et comment fonctionne-t-il ? 

Dans cet article, nous allons explorer le concept de clustering hiérarchique et fournir des exemples concrets pour vous aider à mieux comprendre ses applications.

Qu'est-ce que le regroupement hiérarchique ?

Le regroupement hiérarchique est un algorithme d'apprentissage non supervisé d'apprentissage non supervisé utilisé pour regrouper des points de données similaires en grappes. Il construit une hiérarchie de grappes à plusieurs niveaux, soit en fusionnant des grappes plus petites en grappes plus grandes (agglomération), soit en divisant une grande grappe en grappes plus petites (division). Il en résulte une structure arborescente appelée dendrogramme.

Un dendrogramme est une représentation visuelle qui illustre la disposition des groupes et leurs relations mutuelles. La hauteur des branches d'un dendrogramme représente la distance ou la dissimilarité à laquelle les groupes fusionnent. Les hauteurs inférieures indiquent que les grappes sont reliées à de plus petites distances, ce qui représente une plus grande similarité.

L'importance du regroupement hiérarchique dans l'apprentissage automatique

Le regroupement hiérarchique est particulièrement utile lorsque le nombre de grappes n'est pas connu à l'avance. Il permet aux analystes de données et aux scientifiques des données d'explorer visuellement la structure des données à l'aide de dendrogrammes.

Cette technique est également capable de découvrir des groupes imbriqués et est largement utilisée dans des domaines tels que la génomique, la segmentation de la clientèle et l'organisation des documents.

Par exemple, supposons que nous disposions d'un ensemble de données relatives aux achats effectués par les clients. Grâce à la classification hiérarchique, nous pouvons regrouper les clients ayant des habitudes d'achat similaires et identifier des segments de marché potentiels pour des stratégies de marketing ciblées.

Regroupement hiérarchique vs K-Means

Lorsqu'il s'agit d'effectuer des tâches de regroupement, la plupart des gens sont indécis quant aux deux méthodes principales : Regroupement hiérarchique ou Regroupement par K-moyennes.

Mais qu'est-ce qui les différencie ? Pour y voir plus clair, examinons leurs différences ci-dessous.

• K-Means:
• Le nombre de grappes doit être défini avant l'exécution.
• Efficace et évolutif pour les grands ensembles de données.
• On suppose que les grappes sont sphériques et de taille égale.
• Regroupement hiérarchique:
• Ne nécessite pas un nombre prédéfini de grappes.
• Plus facile à interpréter grâce aux dendrogrammes.
• Plus lent sur les grands ensembles de données, mais meilleur pour l'exploration de la structure.

Lorsque l'on compare les deux, certains domaines font du clustering hiérarchique une option de choix.

Voici quelques domaines dans lesquels le regroupement hiérarchique est efficace :

• Flexibilité dans la sélection des grappes à l'aide de dendrogrammes.
• Idéal pour les petits ensembles de données ou lorsqu'une hiérarchie visuelle est nécessaire.
• Traite les formes complexes des grappes.

Cependant, elle peut présenter certains inconvénients, tels que :

• Coûteux sur le plan informatique
• Sensible aux données bruyantes et aux valeurs aberrantes.

Vous pouvez vous poser la question : Quand dois-je utiliser la classification hiérarchique ?

Le clustering hiérarchique est un excellent choix pour les applications suivantes :

• Analyse exploratoire des données
• Analyse du profil d'expression génétique
• Segmentation du marché avec des ensembles de données de taille moyenne

Types de classification hiérarchique

Dans la technique du regroupement hiérarchique, vous trouverez plusieurs types de regroupements, chacun apportant des informations et des résultats différents. Les deux principaux types de regroupement hiérarchique sont l'agglomération (de bas en haut) et la division (de haut en bas).

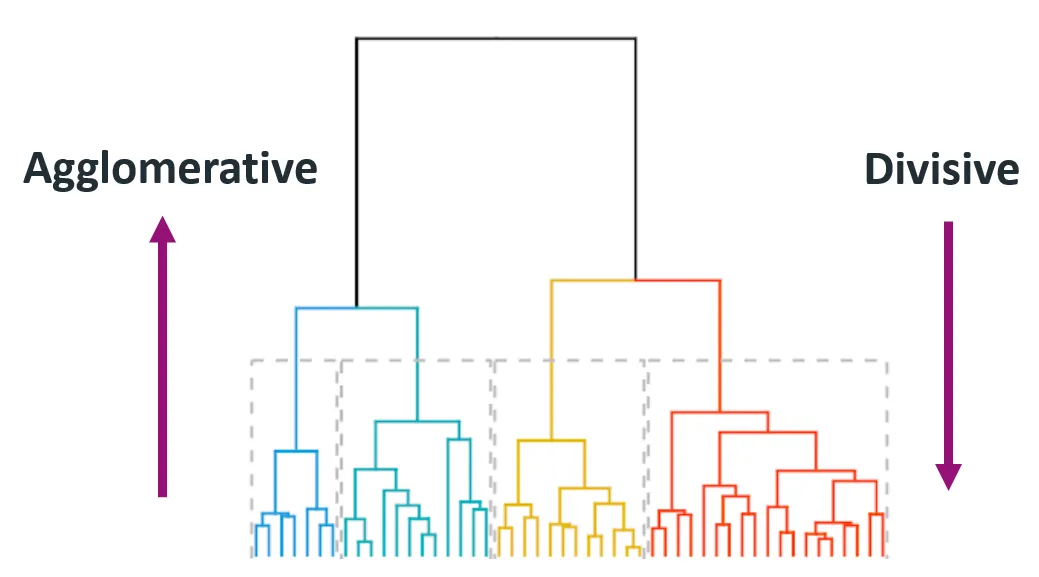
Source : Himanshu Sharma sur Medium

1. Agglomération (de bas en haut)

Le regroupement agglomératif commence par considérer chaque point de données comme une grappe individuelle et fusionne itérativement les paires de grappes les plus proches jusqu'à ce qu'il ne reste qu'une seule grappe ou jusqu'à ce qu'une condition d'arrêt soit remplie (comme un nombre souhaité de grappes).

Cette méthode est également appelée ascendante car elle part du bas (points de données individuels) pour arriver au sommet (grappe finale).

Guide étape par étape:

1. Traitez chaque point de données comme une grappe unique.
2. Calculez les distances par paire entre toutes les grappes.
3. Fusionnez les deux groupes dont la distance est la plus faible.
4. Mettez à jour la matrice de distance pour refléter le nouvel ensemble de grappes.
5. Répétez les étapes 2 à 4 jusqu'à ce que tous les points appartiennent à une seule grappe.

Cette méthode est largement utilisée en raison de sa simplicité et de sa facilité de mise en œuvre.

Voici un exemple de la façon dont cela peut être mis en œuvre en Python :

import numpy as np
from scipy.cluster.hierarchy import linkage, dendrogram, fcluster
import matplotlib.pyplot as plt

# Samples data
data = np.array([[1, 2], [2, 3], [5, 8], [8, 8], [1, 0], [0, 1]])

# Applies agglomerative clustering using Ward's method
Z = linkage(data, method='ward')

# Plots dendrogram
plt.figure(figsize=(8, 4))
dendrogram(Z)
plt.title('Agglomerative Clustering Dendrogram')
plt.xlabel('Data Points')
plt.ylabel('Distance')
plt.show()

# Extracts clusters (e.g., form 2 clusters)
clusters = fcluster(Z, t=2, criterion='maxclust')
print("Cluster assignments:", clusters)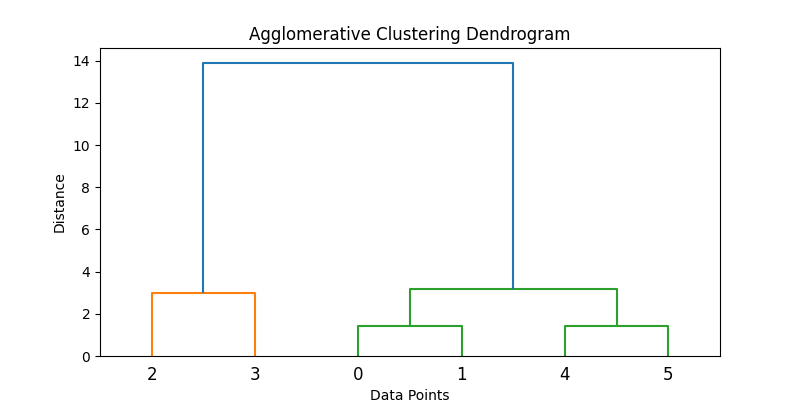

2. Diviser (du haut vers le bas)

Le regroupement divisé part de tous les points de données d'un seul groupe et les divise récursivement en groupes plus petits. Le processus se poursuit jusqu'à ce que chaque point de données se trouve dans son propre groupe.

Elle est également connue sous le nom d'approche descendante, car elle part du sommet (une seule grappe) et la décompose en grappes plus petites.

Guide étape par étape:

1. Commencez par une grande grappe contenant tous les points de données.
2. Divisez le groupe en deux groupes aussi différents que possible.
3. Réappliquez le processus de division de manière récursive à chaque groupe résultant.

Les méthodes de division sont généralement plus coûteuses en termes de calcul en raison de leur nature récursive, et la précision dépend fortement de la stratégie de division. Les méthodes agglomératives sont plus courantes en raison de leur facilité de mise en œuvre et de la généralisation des logiciels.

Note : Le clustering hiérarchique divisé n'est pas aussi facilement pris en charge dans les bibliothèques Python standard que le clustering agglomératif. Une approche consiste à utiliser des algorithmes de regroupement tels que les k-moyennes de manière récursive.

Voici un concept de code d'un fractionnement récursif simulé de type k-means :

from sklearn.cluster import KMeans

def divisive_clustering(data, depth=2):
    if depth == 0 or len(data) <= 1:
        return [data]

    kmeans = KMeans(n_clusters=2, random_state=42).fit(data)
    labels = kmeans.labels_
    cluster1 = data[labels == 0]
    cluster2 = data[labels == 1]

    return divisive_clustering(cluster1, depth - 1) + divisive_clustering(cluster2, depth - 1)

# Run recursive splitting to simulate divisive clustering
split_clusters = divisive_clustering(data, depth=2)
for i, cluster in enumerate(split_clusters):
    print(f"Cluster {i+1} size: {len(cluster)}")

Ce code simplifié illustre une approche conceptuelle du regroupement par division à l'aide de K-Means récursifs. Notez toutefois que les méthodes de division standard telles que DIANA utilisent des critères de division différents.

Concepts et terminologies clés

Le regroupement hiérarchique fait intervenir certains concepts et terminologies clés qu'il est important de comprendre. Pour bien comprendre le processus, nous allons examiner ces concepts plus en détail ci-dessous.

1. Dendrogrammes

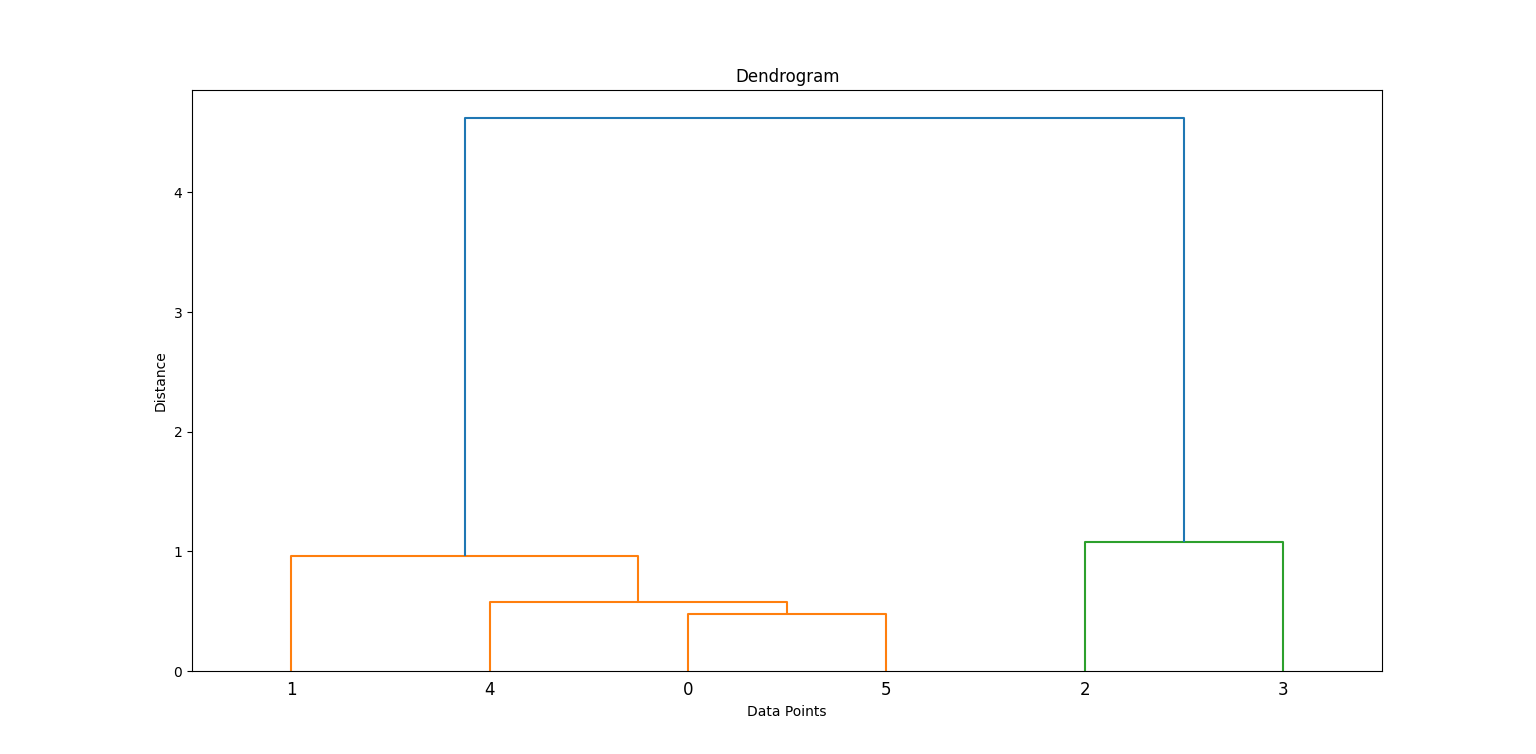
Un dendrogramme est une structure arborescente qui permet de visualiser le processus de regroupement hiérarchique. Chaque niveau de l'arbre représente une opération de fusion ou de scission, et la hauteur des branches représente la distance (ou la dissimilarité) à laquelle les grappes ont été jointes.

Voici pourquoi c'est important :

• Permet l'inspection visuelle des grappes à différents niveaux.
• En "coupant" le dendrogramme à une certaine hauteur, vous pouvez choisir le nombre de groupes qui correspond le mieux aux données.

2. Critères de liaison

Les critères de liaison déterminent la manière dont les distances entre les grappes sont calculées au cours du processus de fusion.

Voici quelques types de critères de liaison :

Liaison unique (minimum)

Ce critère examine la distance entre les points les plus proches de deux grappes. Il peut en résulter des grappes allongées, ressemblant à des chaînes.

from scipy.spatial.distance import pdist, squareform
data = np.array([[1, 2], [2, 3], [5, 8]])
distance_matrix = squareform(pdist(data, metric='euclidean')) 
single_linkage_min = np.min(distance_matrix[0, 1:])
print("Single Linkage Distance between Cluster A (point 1) and Cluster B (point 2, 3):", single_linkage_min)

Attelage complet (maximum)

Ce critère examine la distance entre les points les plus éloignés de deux grappes. Cela tend à produire des grappes compactes et de taille régulière.

single_linkage_max = np.max(distance_matrix[0, 1:])
print("Complete Linkage Distance between Cluster A and B:", single_linkage_max)

Lien moyen (moyenne)

Ce critère examine la distance moyenne entre tous les points d'un groupe et tous les points d'un autre groupe. Cela permet d'obtenir un équilibre entre le lien unique et le lien complet.

average_linkage = np.mean(distance_matrix[0, 1:])
print("Average Linkage Distance between Cluster A and B:", average_linkage)

Ces exemples simplifiés illustrent la manière dont les distances sont initialement calculées. Toutefois, lors du regroupement, ces critères (lien unique, complet, moyen) appliquent les distances de manière itérative entre des groupes entiers, et non pas seulement entre des points individuels.

Méthode de Ward

La méthode de Ward est une variante de l'approche du lien moyen qui minimise la somme des différences quadratiques au sein de toutes les grappes. Elle tend à produire des grappes de taille plus homogène que les autres méthodes. En outre, elle donne souvent lieu à des grappes sphériques bien séparées.

from scipy.cluster.hierarchy import linkage
linkage_ward = linkage(data, method='ward')
print("Ward's Linkage Matrix:\n", linkage_ward)

Chaque méthode a ses propres atouts et doit être choisie en fonction des données et du cas d'utilisation.

3. Mesures de distance

La métrique de distance utilisée influe considérablement sur le résultat du regroupement.

Distance euclidienne

La distance distance euclidienne est la distance en ligne droite entre deux points dans un espace multidimensionnel. Il s'agit de la mesure de distance la plus couramment utilisée, en particulier pour les données géométriquement distribuées.

Distance de Manhattan

La distance de Manhattan, également connue sous le nom de distance de taxi ou distance L1, est la somme des différences absolues entre les dimensions. Il est utile pour les données en grille telles que les pâtés de maisons ou les transactions financières.

Similitude du cosinus

Similitude de cosinus mesure le cosinus de l'angle entre deux vecteurs non nuls. Cette métrique est idéale pour les données textuelles ou lorsque la magnitude n'a pas d'importance (par exemple, les vecteurs de fréquence de mots).

Implémentation du clustering hiérarchique en Python

Dans cette section, nous verrons une mise en œuvre pratique du clustering hiérarchique agglomératif à l'aide de Python. Nous couvrirons tous les aspects, du prétraitement des données à la visualisation des résultats à l'aide d'un dendrogramme.

Bibliothèques

Nous commençons par importer les bibliothèques nécessaires :

import numpy as np
import pandas as pd
from scipy.cluster.hierarchy import dendrogram, linkage, fcluster
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt

Voici ce que nous avons importé dans le code ci-dessus :

• numpy et pandas pour la manipulation des données
• scipy.cluster.hierarchy pour le regroupement et la génération de dendrogrammes
• sklearn.preprocessing.StandardScaler pour la mise à l'échelle des caractéristiques
• matplotlib pour la visualisation

Exemple de données

Avant de commencer notre analyse, créons un jeu de données de points 2D et mettons-le à l'échelle. La mise à l'échelle est cruciale pour les algorithmes basés sur la distance.

Voici à quoi ressemblerait notre échantillon de données.

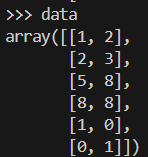
data = np.array([[1, 2], [2, 3], [5, 8], [8, 8], [1, 0], [0, 1]])
scaler = StandardScaler()
data_scaled = scaler.fit_transform(data)

Voici à quoi ressemble le tableau de données après sa mise à l'échelle.

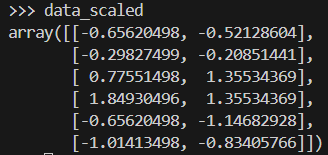
Génération d'une matrice de liaison et d'un dendrogramme

Nous appliquons la méthode de Ward pour générer une matrice de liens, qui contient des informations sur le regroupement hiérarchique. Ensuite, nous graphons un dendrogramme.

linkage_matrix = linkage(data_scaled, method='ward')
plt.figure(figsize=(8, 4))
dendrogram(linkage_matrix)
plt.title('Dendrogram')
plt.xlabel('Data Points')
plt.ylabel('Distance')
plt.show()

Dans le code ci-dessus, linkage construit la hiérarchie des grappes et dendrogram aide à visualiser la façon dont les grappes ont été formées.

En examinant où les lignes verticales sont les plus longues avant une fusion, nous pouvons décider où "couper" pour former des grappes. Recherchez la ligne verticale la plus haute qui ne croise aucune autre grappe. C'est ici que vous devrez faire la part des choses.

Dans ce cas, vous devrez couper 2 grappes.

Création de clusters

Ensuite, nous coupons le dendrogramme pour obtenir un nombre spécifique de grappes à l'aide de fcluster:

clusters = fcluster(linkage_matrix, t=2, criterion='maxclust')
print(clusters)

plt.scatter(data_scaled[:, 0], data_scaled[:, 1], c=clusters, cmap='rainbow')
plt.title('Clusters')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.show()

Cela permet d'affecter chaque point de données à l'un des deux groupes.

Quelques informations supplémentaires sur le code :

• t=2: Spécifie le nombre de grappes souhaité.
• criterion='maxclust': Assure que nous obtenons exactement t clusters.

Vous pouvez modifier t pour expérimenter différents nombres de grappes.

Exemple pratique : Segmentation de la clientèle

Le regroupement hiérarchique est généralement utilisé pour la segmentation de la clientèle. Voyons ce que cela donne dans la pratique.

1. Aperçu de l'ensemble des données

Simulons un ensemble de données représentant des clients avec deux caractéristiques : l'âge et le revenu. Nous utiliserons make_blobs pour générer ces données synthétiques.

from sklearn.datasets import make_blobs
X, _ = make_blobs(n_samples=100, centers=3, n_features=2, random_state=42)

2. Prétraitement

Ensuite, nous devrons normaliser les caractéristiques afin de normaliser les échelles et d'améliorer la précision du regroupement.

scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

Voici à quoi ressemblent les données mises à l'échelle :

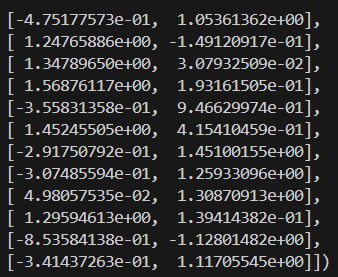
3. Application de la classification hiérarchique

Maintenant que nos données ont été traitées, nous allons tracer le dendrogramme pour visualiser la formation des groupes.

linkage_matrix = linkage(X_scaled, method='ward')
plt.figure(figsize=(10, 5))
dendrogram(linkage_matrix)
plt.title('Customer Dendrogram')
plt.xlabel('Sample Index')
plt.ylabel('Distance')
plt.show()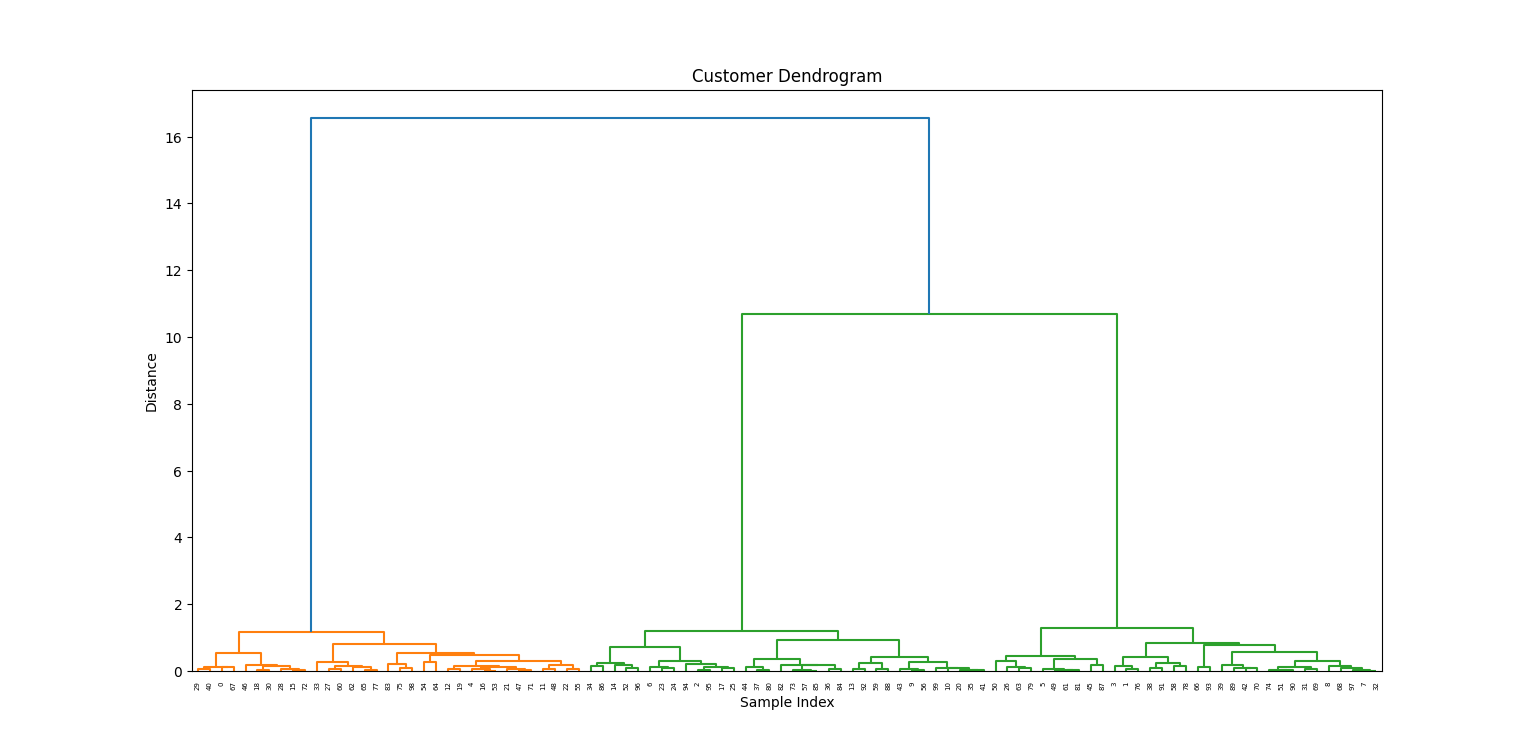

4. Interprétation des résultats

À partir du dendrogramme, nous choisissons une hauteur pour "couper" et créer trois groupes :

labels = fcluster(linkage_matrix, t=3, criterion='maxclust')
plt.scatter(X_scaled[:, 0], X_scaled[:, 1], c=labels, cmap='rainbow')
plt.title('Customer Segments')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.show()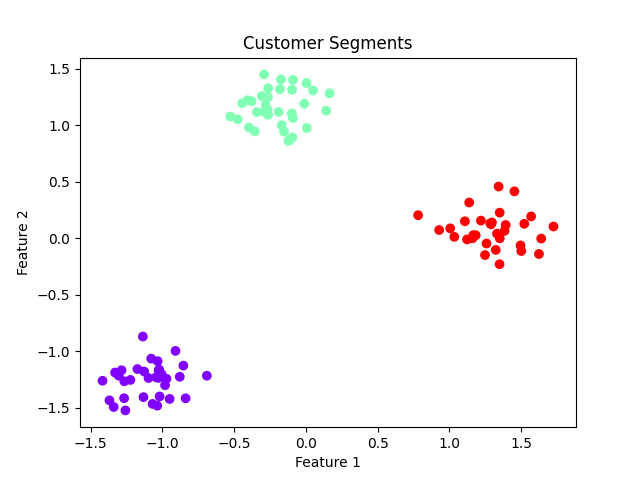

Implications pour les entreprises :

• Les groupes pourraient représenter des groupes de clients tels que les clients soucieux de leur budget, les clients de niveau intermédiaire et les clients haut de gamme.
• Permet de personnaliser le marketing et d'améliorer les stratégies de relations avec les clients.

Avantages et limites de la classification hiérarchique

Le choix de la classification hiérarchique pour votre analyse présente plusieurs avantages et limites. 

Vous trouverez ci-dessous quelques exemples courants :

Pour

• Il n'est pas nécessaire de spécifier le nombre de grappes: Vous pouvez choisir après inspection visuelle du dendrogramme.
• Visualisation intuitive: Les dendrogrammes permettent de comprendre comment les groupes se forment.
• Flexible: Peut gérer différentes formes de grappes en fonction des liens et des métriques de distance.

Cons

• : Il n'est pas idéal pour les grands ensembles de données.
• Sensible au bruit et aux valeurs aberrantes: Quelques valeurs aberrantes peuvent fausser le dendrogramme de manière significative.
• Pas de réaffectation: Une fois qu'une fusion est effectuée, elle ne peut être annulée, ce qui peut conduire à un regroupement sous-optimal.

Conclusion

Le regroupement hiérarchique est une technique de regroupement polyvalente et interprétable, particulièrement utile dans l'analyse exploratoire des données et dans des domaines tels que la génomique et la segmentation de la clientèle. Malgré son coût de calcul, sa force réside dans sa capacité à découvrir des groupes imbriqués et dans sa flexibilité à choisir le nombre de groupes post-hoc par le biais de la visualisation du dendrogramme.

Pour les ensembles de données de petite et moyenne taille où l'interprétabilité est essentielle, le clustering hiérarchique reste une méthode de choix pour les scientifiques et les analystes de données.

Vous souhaitez en savoir plus sur les détails de l'apprentissage automatique ? Notre Fondamentaux de l'apprentissage automatique en Python cursus et Introduction au clustering hiérarchique en Python sont d'excellents points de départ.