Agrupación jerárquica: Concepto general con ejemplos

Así que te acaban de encargar que analices un gran conjunto de datos, y te piden que proporciones un análisis de conglomerados en profundidad. Te has encontrado con el término "agrupación jerárquica", pero ¿qué es exactamente y cómo funciona? 

En este artículo, exploraremos el concepto de agrupación jerárquica y proporcionaremos ejemplos reales para ayudarte a comprender mejor sus aplicaciones.

¿Qué es la Agrupación Jerárquica?

La agrupación jerárquica es un aprendizaje no supervisado no supervisado para agrupar puntos de datos similares en clusters. Construye una jerarquía multinivel de conglomerados fusionando conglomerados más pequeños en otros más grandes (aglomerativo) o dividiendo un conglomerado grande en otros más pequeños (divisivo). El resultado es una estructura arborescente denominada dendrograma.

Un dendrograma es una representación visual que ilustra la disposición de los conglomerados y sus relaciones entre sí. La altura de las ramas en un dendrograma representa la distancia o disimilitud a la que se fusionan los conglomerados. Las alturas más bajas indican clusters unidos a distancias menores, por lo que representan una mayor similitud.

Por qué es importante la agrupación jerárquica en el aprendizaje automático

La agrupación jerárquica es especialmente útil cuando no se conoce de antemano el número de conglomerados. Permite analistas de datos y científicos de datos explorar visualmente la estructura de los datos mediante dendrogramas.

Esta técnica también es capaz de descubrir conglomerados anidados y se utiliza ampliamente en campos como la genómica, la segmentación de clientes y la organización de documentos.

Por ejemplo, supongamos que tenemos un conjunto de datos de registros de compras de clientes. Mediante la agrupación jerárquica, podemos agrupar en conglomerados a clientes con pautas de compra similares e identificar segmentos de mercado potenciales para estrategias de marketing específicas.

Agrupación jerárquica frente a K-Means

Cuando se trata de tareas de agrupación, la mayoría se decanta por dos métodos principales: Agrupación jerárquica o agrupación de K-means.

Pero, ¿qué les hace diferentes? Veamos a continuación sus diferencias para tener una idea más clara.

• K-Means:
• Requiere que se defina el número de clusters antes de ejecutarlo.
• Eficaz y escalable para grandes conjuntos de datos.
• Supone que los racimos son esféricos y de igual tamaño.
• Agrupación jerárquica:
• No requiere un número predefinido de agrupaciones.
• Más interpretable gracias a los dendrogramas.
• Más lento en grandes conjuntos de datos, pero mejor para explorar la estructura.

Al compararlas, algunas áreas hacen que la agrupación jerárquica sea una opción destacada.

He aquí algunas áreas en las que la agrupación jerárquica es buena:

• Flexibilidad en la selección de conglomerados mediante dendrogramas.
• Bueno para conjuntos de datos pequeños o cuando se necesita una jerarquía visual.
• Maneja formas de racimo complejas.

Sin embargo, puede tener algunos inconvenientes, como:

• Costoso desde el punto de vista informático
• Sensible a los datos ruidosos y a los valores atípicos.

Te preguntarás: ¿Cuándo debo utilizar la agrupación jerárquica?

La agrupación jerárquica es una opción excelente en las siguientes aplicaciones:

• Análisis exploratorio de datos
• Análisis del patrón de expresión génica
• Segmentación del mercado con conjuntos de datos de tamaño moderado

Tipos de agrupación jerárquica

Dentro de la técnica de la agrupación jerárquica, encontrarás varios tipos, cada uno de los cuales proporciona perspectivas y resultados diferentes. Los dos tipos principales de agrupación jerárquica son la aglomerativa (ascendente) y la divisiva (descendente).

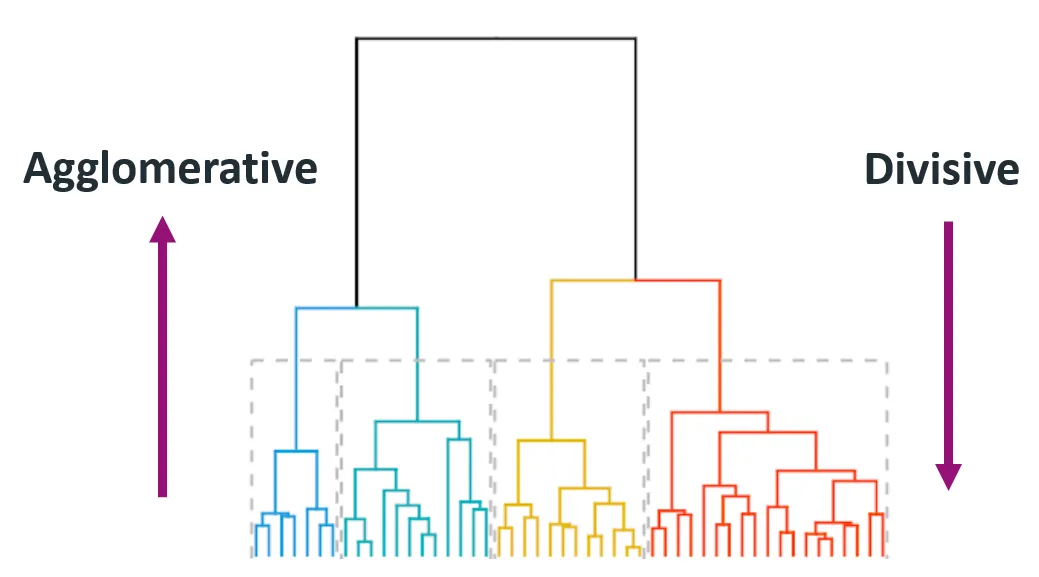
Fuente: Himanshu Sharma en Medium

1. Aglomerativo (ascendente)

La agrupación aglomerativa comienza con cada punto de datos como un conglomerado individual y fusiona iterativamente el par de conglomerados más cercano hasta que sólo queda un conglomerado o hasta que se cumple una condición de parada (como un número deseado de conglomerados).

Este método también se denomina ascendente, porque empieza desde abajo (puntos de datos individuales) y va subiendo hasta llegar a la cima (conglomerado final).

Guía paso a paso:

1. Trata cada punto de datos como un conglomerado único.
2. Calcula las distancias por pares entre todos los conglomerados.
3. Fusiona los dos conglomerados con la menor distancia.
4. Actualiza la matriz de distancias para reflejar el nuevo conjunto de conglomerados.
5. Repite los pasos 2-4 hasta que todos los puntos pertenezcan a un único cluster.

Este método se utiliza mucho por su sencillez y facilidad de aplicación.

Aquí tienes un ejemplo de cómo se puede implementar esto en Python:

import numpy as np
from scipy.cluster.hierarchy import linkage, dendrogram, fcluster
import matplotlib.pyplot as plt

# Samples data
data = np.array([[1, 2], [2, 3], [5, 8], [8, 8], [1, 0], [0, 1]])

# Applies agglomerative clustering using Ward's method
Z = linkage(data, method='ward')

# Plots dendrogram
plt.figure(figsize=(8, 4))
dendrogram(Z)
plt.title('Agglomerative Clustering Dendrogram')
plt.xlabel('Data Points')
plt.ylabel('Distance')
plt.show()

# Extracts clusters (e.g., form 2 clusters)
clusters = fcluster(Z, t=2, criterion='maxclust')
print("Cluster assignments:", clusters)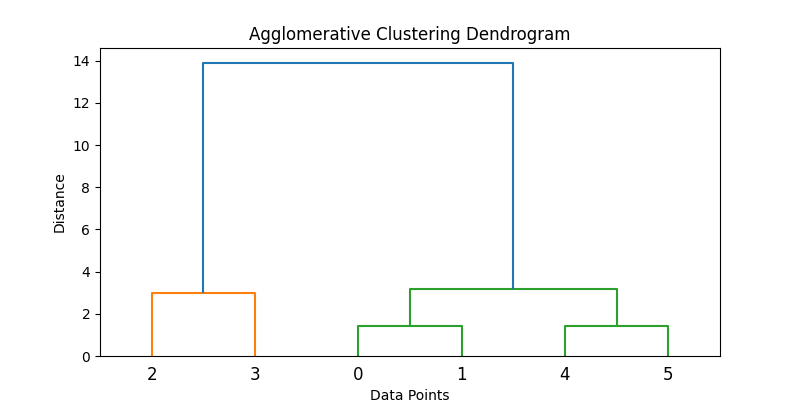

2. Divisivo (de arriba abajo)

La agrupación divisiva comienza con todos los puntos de datos de un único conglomerado y los divide recursivamente en conglomerados más pequeños. El proceso continúa hasta que cada punto de datos está en su propio conglomerado individual.

También se conoce como enfoque descendente, ya que comienza en la parte superior (conglomerado único) y lo descompone en conglomerados más pequeños.

Guía paso a paso:

1. Empieza con un gran conglomerado que contenga todos los puntos de datos.
2. Divide el grupo en dos que sean lo más diferentes posible.
3. Vuelve a aplicar el proceso de división recursivamente a cada grupo resultante.

Los métodos divisivos suelen ser más caros computacionalmente debido a su naturaleza recursiva, y la precisión depende en gran medida de la estrategia de división. Los métodos aglomerativos son más comunes debido a la facilidad de aplicación y al amplio soporte de software.

Nota: La agrupación jerárquica divisoria no se soporta tan fácilmente en las bibliotecas estándar de Python como la agrupación aglomerativa. Un enfoque consiste en utilizar algoritmos de agrupación como k-means de forma recursiva.

Aquí tienes un concepto de código de una división k-means recursiva simulada:

from sklearn.cluster import KMeans

def divisive_clustering(data, depth=2):
    if depth == 0 or len(data) <= 1:
        return [data]

    kmeans = KMeans(n_clusters=2, random_state=42).fit(data)
    labels = kmeans.labels_
    cluster1 = data[labels == 0]
    cluster2 = data[labels == 1]

    return divisive_clustering(cluster1, depth - 1) + divisive_clustering(cluster2, depth - 1)

# Run recursive splitting to simulate divisive clustering
split_clusters = divisive_clustering(data, depth=2)
for i, cluster in enumerate(split_clusters):
    print(f"Cluster {i+1} size: {len(cluster)}")

Este código simplificado ilustra un enfoque conceptual de la agrupación divisoria mediante K-means recursivo. Ten en cuenta, sin embargo, que los métodos divisorios estándar, como DIANA, utilizan criterios de división diferentes.

Conceptos clave y terminología

La agrupación jerárquica implica algunos conceptos y terminologías clave que es importante comprender. Para comprender bien el proceso, repasaremos estos conceptos con más detalle a continuación.

1. Dendrogramas

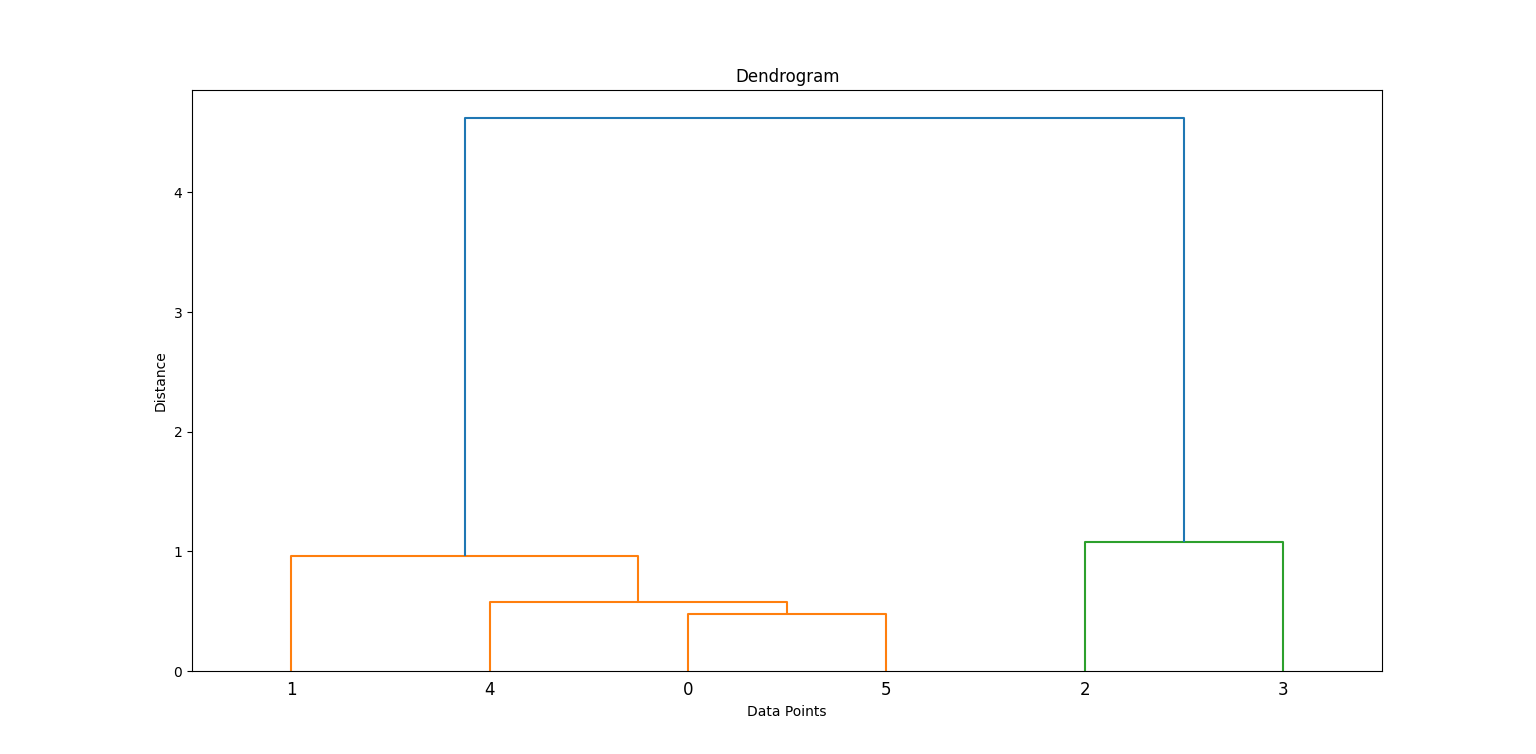
Un dendrograma es una estructura en forma de árbol que visualiza el proceso de agrupación jerárquica. Cada nivel del árbol representa una operación de fusión o división, y la altura de las ramas representa la distancia (o disimilitud) a la que se unieron los conglomerados.

He aquí por qué es importante:

• Permite la inspección visual de agrupaciones a distintos niveles.
• Al "cortar" el dendrograma a una altura determinada, puedes elegir el número de conglomerados que mejor se ajuste a los datos.

2. Criterios de vinculación

Los criterios de enlace determinan cómo se calculan las distancias entre los conglomerados durante el proceso de fusión.

He aquí algunos tipos de criterios de vinculación:

Enganche simple (mínimo)

Este criterio tiene en cuenta la distancia entre los puntos más cercanos de dos conglomerados. Esto puede dar lugar a racimos alargados en forma de cadena.

from scipy.spatial.distance import pdist, squareform
data = np.array([[1, 2], [2, 3], [5, 8]])
distance_matrix = squareform(pdist(data, metric='euclidean')) 
single_linkage_min = np.min(distance_matrix[0, 1:])
print("Single Linkage Distance between Cluster A (point 1) and Cluster B (point 2, 3):", single_linkage_min)

Enlace completo (máximo)

Este criterio tiene en cuenta la distancia entre los puntos más alejados de dos conglomerados. Esto tiende a producir racimos compactos y de tamaño uniforme.

single_linkage_max = np.max(distance_matrix[0, 1:])
print("Complete Linkage Distance between Cluster A and B:", single_linkage_max)

Enlace medio (media)

Este criterio considera la distancia media entre todos los puntos de un conglomerado y todos los puntos de otro. Así se consigue un equilibrio entre la vinculación simple y la completa.

average_linkage = np.mean(distance_matrix[0, 1:])
print("Average Linkage Distance between Cluster A and B:", average_linkage)

Estos ejemplos simplificados ilustran cómo se calculan inicialmente las distancias. Sin embargo, durante la agrupación, estos criterios (vinculación única, completa, media) aplican distancias de forma iterativa entre agrupaciones enteras, no sólo entre puntos individuales.

Método de Ward

El método de Ward es una variación del enfoque de vinculación media que minimiza la suma de las diferencias al cuadrado dentro de todos los conglomerados. Tiende a producir agrupaciones de tamaño más uniforme en comparación con otros métodos. También suele dar lugar a grupos esféricos bien separados.

from scipy.cluster.hierarchy import linkage
linkage_ward = linkage(data, method='ward')
print("Ward's Linkage Matrix:\n", linkage_ward)

Cada método tiene sus puntos fuertes y debe elegirse en función de los datos y del caso de uso.

3. Métricas de distancia

La métrica de distancia utilizada influye significativamente en el resultado de la agrupación.

Distancia euclidiana

La dirección distancia euclidiana es la distancia rectilínea entre dos puntos en un espacio multidimensional. Es la métrica de distancia más utilizada, especialmente para datos distribuidos geométricamente.

Distancia a Manhattan

La distancia Manhattan, también conocida como distancia taxi o L1, es la suma de las diferencias absolutas entre dimensiones. Es útil para datos en forma de cuadrícula, como manzanas de una ciudad o transacciones financieras.

Similitud coseno

Similitud del coseno mide el coseno del ángulo entre dos vectores distintos de cero. Esta métrica es ideal para datos de texto o cuando la magnitud no importa (por ejemplo, vectores de frecuencia de palabras).

Implementación de la agrupación jerárquica en Python

En esta sección, recorreremos una implementación práctica de la agrupación jerárquica aglomerativa utilizando Python. Lo cubriremos todo, desde el preprocesamiento de los datos hasta la visualización de los resultados mediante un dendrograma.

Bibliotecas

Comenzamos importando las bibliotecas necesarias:

import numpy as np
import pandas as pd
from scipy.cluster.hierarchy import dendrogram, linkage, fcluster
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt

Esto es lo que hemos importado en el código anterior:

• numpy y pandas para la manipulación de datos
• scipy.cluster.hierarchy para la agrupación y la generación de dendrogramas
• sklearn.preprocessing.StandardScaler para el escalado de rasgos
• matplotlib para la visualización

Datos de la muestra

Antes de empezar nuestro análisis, vamos a crear un conjunto de datos de juguete de puntos 2D y a escalarlo. El escalado es crucial para los algoritmos basados en la distancia.

Este es el aspecto que tendría nuestro conjunto de datos de muestra.

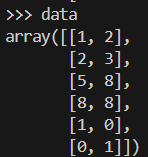
data = np.array([[1, 2], [2, 3], [5, 8], [8, 8], [1, 0], [0, 1]])
scaler = StandardScaler()
data_scaled = scaler.fit_transform(data)

Este es el aspecto de la matriz de datos una vez escalada.

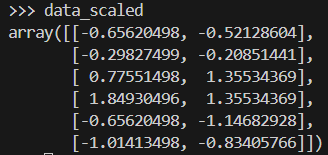
Generar una matriz de enlace y un dendrograma

Aplicamos el método de Ward para generar una matriz de vinculación, que contiene información de agrupación jerárquica. A continuación, trazamos un dendrograma.

linkage_matrix = linkage(data_scaled, method='ward')
plt.figure(figsize=(8, 4))
dendrogram(linkage_matrix)
plt.title('Dendrogram')
plt.xlabel('Data Points')
plt.ylabel('Distance')
plt.show()

En el código anterior, linkage construye la jerarquía de clusters, y dendrogram ayuda a visualizar cómo se formaron los clusters.

Examinando dónde son más largas las líneas verticales antes de una fusión, podemos decidir dónde "cortar" para formar agrupaciones. Busca la línea vertical más alta que no se cruce con ningún otro grupo. Aquí es donde tendrás que hacer el corte.

En este caso, tendrás que cortar en 2 grupos.

Crear agrupaciones

A continuación, cortamos el dendrograma para obtener un número determinado de conglomerados utilizando fcluster:

clusters = fcluster(linkage_matrix, t=2, criterion='maxclust')
print(clusters)

plt.scatter(data_scaled[:, 0], data_scaled[:, 1], c=clusters, cmap='rainbow')
plt.title('Clusters')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.show()

Esto asigna cada punto de datos a uno de los dos conglomerados.

Información adicional sobre el código:

• t=2: Especifica el número de clusters deseado.
• criterion='maxclust': Garantiza que obtenemos exactamente t racimos.

Puedes cambiar t para experimentar con distintos números de grupos.

Ejemplo práctico: Segmentación de clientes

La agrupación jerárquica se suele utilizar en la segmentación de clientes. Veamos cómo queda esto en una aplicación práctica.

1. Resumen del conjunto de datos

Vamos a simular un conjunto de datos que representa a clientes con dos características: edad e ingresos. Utilizaremos make_blobs para generar estos datos sintéticos.

from sklearn.datasets import make_blobs
X, _ = make_blobs(n_samples=100, centers=3, n_features=2, random_state=42)

2. Preprocesamiento

A continuación, tendremos que normalizar las características para normalizar las escalas y mejorar la precisión de la agrupación.

scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

Este es el aspecto de los datos escalados:

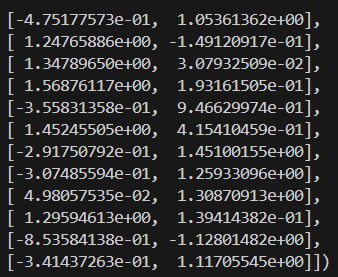
3. Aplicación de la agrupación jerárquica

Ahora que nuestros datos han sido procesados, trazaremos el dendrograma para visualizar cómo se forman los clusters.

linkage_matrix = linkage(X_scaled, method='ward')
plt.figure(figsize=(10, 5))
dendrogram(linkage_matrix)
plt.title('Customer Dendrogram')
plt.xlabel('Sample Index')
plt.ylabel('Distance')
plt.show()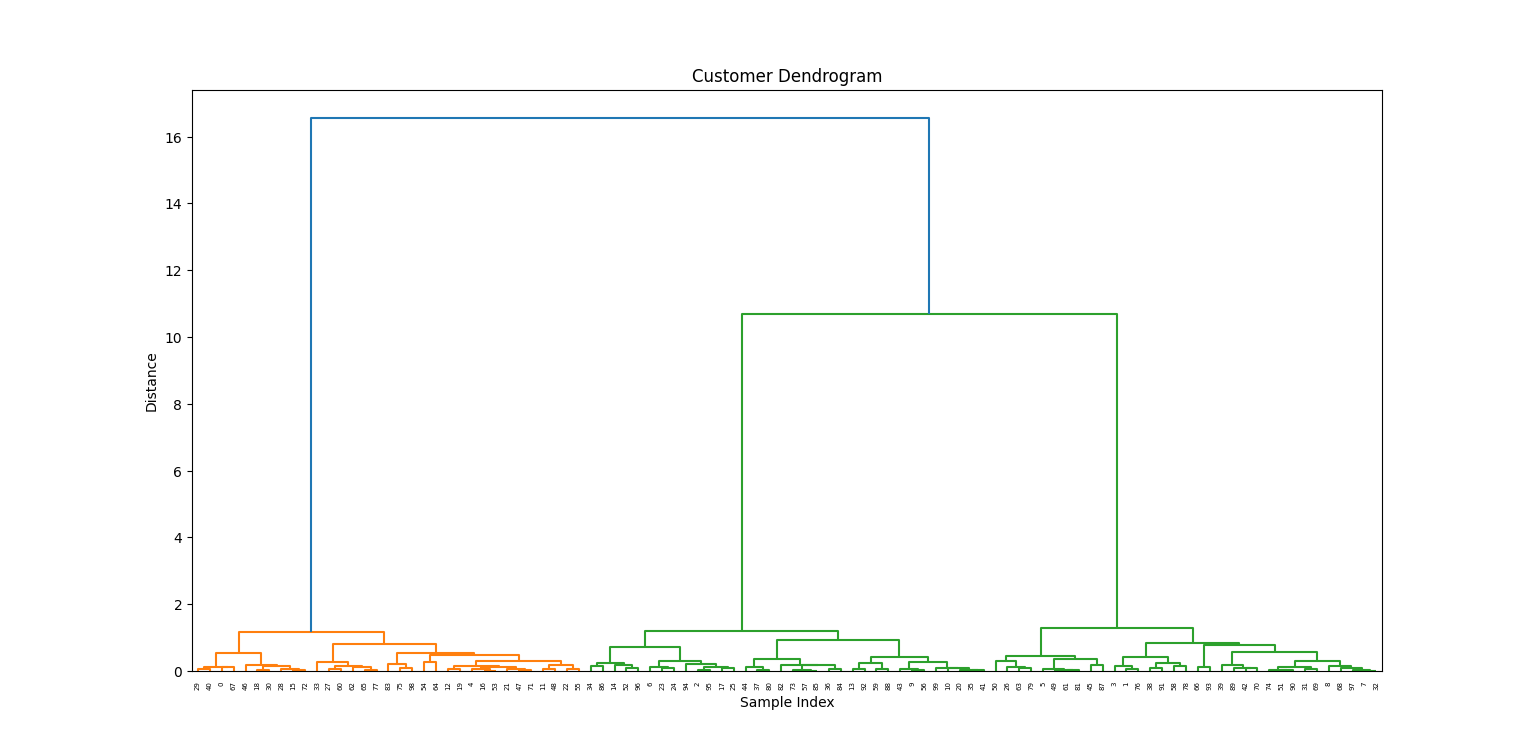

4. Interpretar los resultados

A partir del dendrograma, elegimos una altura para "cortar" y crear tres conglomerados:

labels = fcluster(linkage_matrix, t=3, criterion='maxclust')
plt.scatter(X_scaled[:, 0], X_scaled[:, 1], c=labels, cmap='rainbow')
plt.title('Customer Segments')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.show()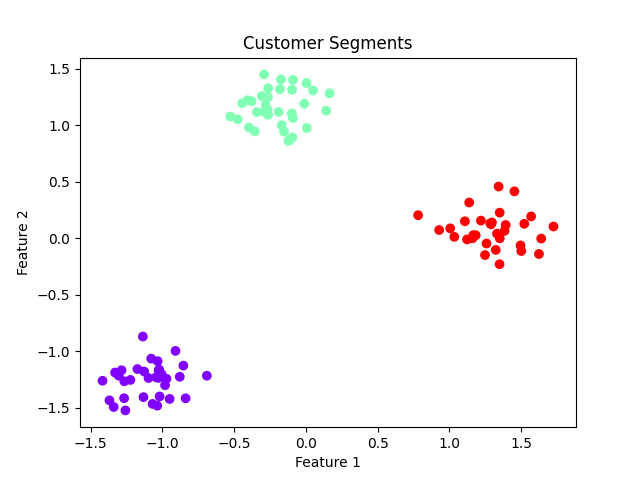

Implicaciones empresariales:

• Los clusters podrían representar grupos de clientes como los que se preocupan por el presupuesto, los de nivel medio y los premium.
• Permite el marketing personalizado y la mejora de las estrategias de relación con los clientes.

Ventajas y limitaciones de la agrupación jerárquica

Elegir la agrupación jerárquica para tu análisis tiene varias ventajas y limitaciones. 

Mira a continuación algunos de los más comunes:

Pros

• No es necesario especificar el número de grupos: Puedes elegir tras una inspección visual del dendrograma.
• Visualización intuitiva: Los dendrogramas ayudan a comprender cómo se forman los conglomerados.
• Flexible: Puede manejar varias formas de conglomerados en función de las métricas de vinculación y distancia.

Contras

• Computacionalmente intensivo: No es ideal para grandes conjuntos de datos.
• Sensible al ruido y a los valores atípicos: Unos pocos valores atípicos pueden distorsionar significativamente el dendrograma.
• No hay reasignación: Una vez realizada una fusión, no se puede deshacer, lo que podría dar lugar a una agrupación subóptima.

Conclusión

La agrupación jerárquica es una técnica de agrupación versátil e interpretable, especialmente útil en el análisis exploratorio de datos y en ámbitos como la genómica y la segmentación de clientes. A pesar de su coste computacional, su fuerza reside en la capacidad de descubrir agrupaciones anidadas y su flexibilidad para elegir el número de agrupaciones post-hoc mediante la visualización del dendrograma.

Para los conjuntos de datos pequeños y medianos en los que la interpretabilidad es clave, la agrupación jerárquica sigue siendo un método al que recurren tanto los científicos de datos como los analistas.

¿Quieres saber más sobre los detalles del aprendizaje automático? Nuestro Fundamentos de Aprendizaje Automático en Python y Introducción a la agrupación jerárquica en Python son excelentes puntos de partida.