Clusterização hierárquica: Visão geral do conceito com exemplos

Então, você acabou de receber a tarefa de analisar um grande conjunto de dados e precisa fornecer uma análise de cluster profunda. Você já se deparou com o termo "agrupamento hierárquico", mas o que ele é exatamente e como funciona? 

Neste artigo, exploraremos o conceito de agrupamento hierárquico e forneceremos exemplos reais para ajudar você a entender melhor suas aplicações.

O que é clusterização hierárquica?

O agrupamento hierárquico é uma aprendizado não supervisionado usado para agrupar pontos de dados semelhantes em clusters. Ele cria uma hierarquia multinível de clusters mesclando clusters menores em clusters maiores (aglomerativo) ou dividindo um cluster grande em clusters menores (divisivo). Isso resulta em uma estrutura semelhante a uma árvore, conhecida como dendrograma.

Um dendrograma é uma representação visual que ilustra a disposição dos clusters e suas relações entre si. A altura dos ramos em um dendrograma representa a distância ou a dissimilaridade na qual os grupos se fundem. Alturas mais baixas indicam clusters unidos a distâncias menores, representando, portanto, maior similaridade.

Por que o agrupamento hierárquico é importante no machine learning?

O clustering hierárquico é particularmente útil quando o número de clusters não é conhecido de antemão. Ele permite que analistas de dados e cientistas de dados explorem visualmente a estrutura dos dados por meio de dendrogramas.

Essa técnica também é capaz de descobrir clusters aninhados e é amplamente usada em campos como genômica, segmentação de clientes e organização de documentos.

Por exemplo, digamos que temos um conjunto de dados de registros de compras de clientes. Usando o agrupamento hierárquico, podemos agrupar clientes com padrões de compra semelhantes em grupos e identificar segmentos de mercado em potencial para estratégias de marketing direcionadas.

Agrupamento hierárquico vs. K-Means

Quando se trata de tarefas de agrupamento, a maioria está indecisa em relação a dois métodos principais: Agrupamento hierárquico ou agrupamento K-means.

Mas o que os torna diferentes? Vamos examinar suas diferenças abaixo para que você tenha uma visão mais clara.

• K-Means:
• Requer que o número de clusters seja definido antes da execução.
• Eficiente e dimensionável para grandes conjuntos de dados.
• Pressupõe que os clusters são esféricos e têm o mesmo tamanho.
• Clusterização hierárquica:
• Não requer um número predefinido de clusters.
• Mais interpretável devido aos dendrogramas.
• Mais lento em grandes conjuntos de dados, mas melhor para explorar a estrutura.

Ao comparar os dois, algumas áreas fazem com que o clustering hierárquico seja uma opção de destaque.

Aqui estão algumas áreas em que o agrupamento hierárquico é bom:

• Flexibilidade na seleção de clusters usando dendrogramas.
• Ideal para pequenos conjuntos de dados ou quando você precisa de uma hierarquia visual.
• Lida com formas complexas de clusters.

No entanto, ele pode ter algumas desvantagens, como:

• Computacionalmente caro
• Sensível a dados ruidosos e discrepantes.

Você pode se perguntar: Quando devo usar o clustering hierárquico?

O agrupamento hierárquico é uma excelente opção para as seguintes aplicações:

• Análise exploratória de dados
• Análise do padrão de expressão gênica
• Segmentação de mercado com conjuntos de dados de tamanho moderado

Tipos de agrupamento hierárquico

Dentro da técnica de clustering hierárquico, você encontrará vários tipos, sendo que cada um deles fornece insights e resultados diferentes. Os dois principais tipos de agrupamento hierárquico são o aglomerativo (de baixo para cima) e o divisivo (de cima para baixo).

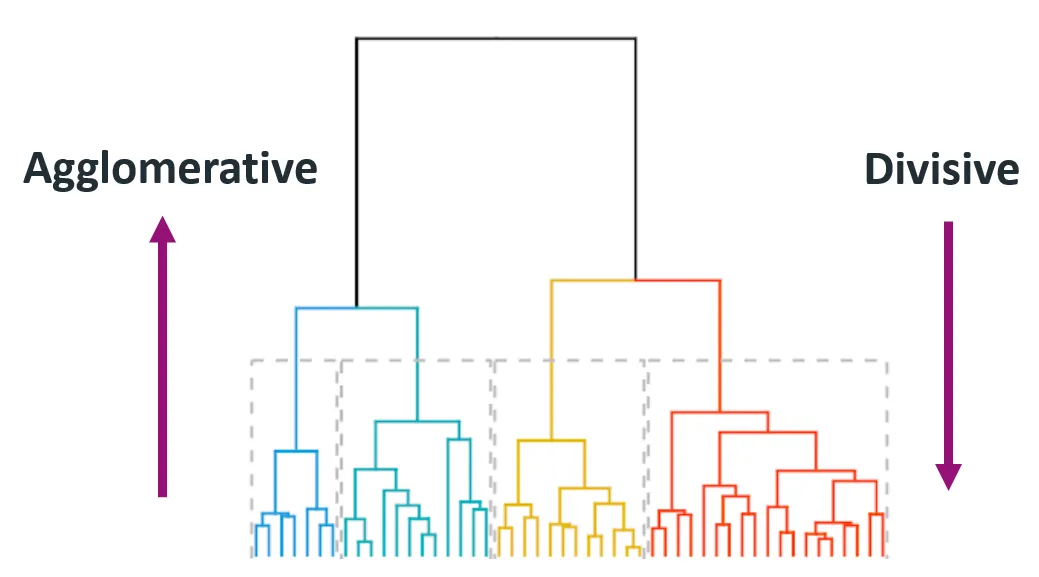
Fonte: Himanshu Sharma no Medium

1. Aglomerativo (de baixo para cima)

O clustering aglomerativo começa com cada ponto de dados como um cluster individual e mescla iterativamente o par de clusters mais próximo até que reste apenas um cluster ou até que uma condição de parada seja atendida (como um número desejado de clusters).

Esse método também é chamado de bottom-up porque começa de baixo para cima (pontos de dados individuais) e vai até o topo (cluster final).

Guia passo a passo:

1. Trate cada ponto de dados como um cluster único.
2. Calcule as distâncias em pares entre todos os clusters.
3. Mesclar os dois clusters com a menor distância.
4. Atualize a matriz de distância para refletir o novo conjunto de clusters.
5. Repita as etapas 2 a 4 até que todos os pontos pertençam a um único cluster.

Esse método é amplamente usado devido à sua simplicidade e facilidade de implementação.

Aqui está um exemplo de como isso pode ser implementado em Python:

import numpy as np
from scipy.cluster.hierarchy import linkage, dendrogram, fcluster
import matplotlib.pyplot as plt

# Samples data
data = np.array([[1, 2], [2, 3], [5, 8], [8, 8], [1, 0], [0, 1]])

# Applies agglomerative clustering using Ward's method
Z = linkage(data, method='ward')

# Plots dendrogram
plt.figure(figsize=(8, 4))
dendrogram(Z)
plt.title('Agglomerative Clustering Dendrogram')
plt.xlabel('Data Points')
plt.ylabel('Distance')
plt.show()

# Extracts clusters (e.g., form 2 clusters)
clusters = fcluster(Z, t=2, criterion='maxclust')
print("Cluster assignments:", clusters)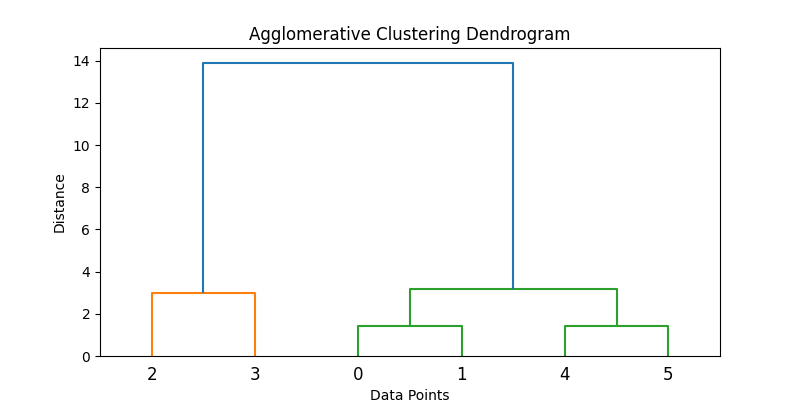

2. Divisivo (de cima para baixo)

O clustering divisivo começa com todos os pontos de dados em um único cluster e os divide recursivamente em clusters menores. O processo continua até que cada ponto de dados esteja em seu próprio cluster individual.

Também é conhecida como abordagem top-down, pois começa no topo (cluster único) e o divide em clusters menores.

Guia passo a passo:

1. Comece com um cluster grande contendo todos os pontos de dados.
2. Divida o cluster em dois que sejam tão diferentes quanto possível.
3. Reaplicar o processo de divisão recursivamente a cada cluster resultante.

Em geral, os métodos divisivos são mais caros do ponto de vista computacional devido à sua natureza recursiva, e a precisão depende muito da estratégia de divisão. Os métodos aglomerativos são mais comuns devido à facilidade de implementação e ao amplo suporte de software.

Observação: O agrupamento hierárquico divisivo não é tão prontamente suportado nas bibliotecas padrão do Python quanto o agrupamento aglomerativo. Uma abordagem é usar algoritmos de agrupamento, como o k-means, de forma recursiva.

Aqui está um conceito de código de uma divisão k-means recursiva simulada:

from sklearn.cluster import KMeans

def divisive_clustering(data, depth=2):
    if depth == 0 or len(data) <= 1:
        return [data]

    kmeans = KMeans(n_clusters=2, random_state=42).fit(data)
    labels = kmeans.labels_
    cluster1 = data[labels == 0]
    cluster2 = data[labels == 1]

    return divisive_clustering(cluster1, depth - 1) + divisive_clustering(cluster2, depth - 1)

# Run recursive splitting to simulate divisive clustering
split_clusters = divisive_clustering(data, depth=2)
for i, cluster in enumerate(split_clusters):
    print(f"Cluster {i+1} size: {len(cluster)}")

Esse código simplificado ilustra uma abordagem conceitual para o agrupamento divisivo usando o K-means recursivo. Observe, entretanto, que os métodos de divisão padrão, como o DIANA, usam critérios de divisão diferentes.

Principais conceitos e terminologias

O agrupamento hierárquico envolve alguns conceitos e terminologias importantes que você precisa entender. Para que você compreenda totalmente o processo, analisaremos esses conceitos em mais detalhes a seguir.

1. Dendrograms

Um dendrograma é uma estrutura semelhante a uma árvore que visualiza o processo de agrupamento hierárquico. Cada nível da árvore representa uma operação de mesclagem ou divisão, e a altura dos ramos representa a distância (ou dissimilaridade) na qual os clusters foram unidos.

Veja por que isso é importante:

• Permite a inspeção visual de clusters em diferentes níveis.
• Ao "cortar" o dendrograma em uma determinada altura, você pode escolher o número de clusters que melhor se adapta aos dados.

2. Critérios de vinculação

Os critérios de ligação determinam como as distâncias entre os clusters são calculadas durante o processo de mesclagem.

Aqui estão alguns tipos de critérios de vinculação:

Ligação única (mínimo)

Esse critério analisa a distância entre os pontos mais próximos de dois clusters. Isso pode resultar em grupos alongados, semelhantes a cadeias.

from scipy.spatial.distance import pdist, squareform
data = np.array([[1, 2], [2, 3], [5, 8]])
distance_matrix = squareform(pdist(data, metric='euclidean')) 
single_linkage_min = np.min(distance_matrix[0, 1:])
print("Single Linkage Distance between Cluster A (point 1) and Cluster B (point 2, 3):", single_linkage_min)

Ligação completa (máximo)

Esse critério analisa a distância entre os pontos mais distantes de dois clusters. Isso tende a produzir cachos compactos e de tamanho uniforme.

single_linkage_max = np.max(distance_matrix[0, 1:])
print("Complete Linkage Distance between Cluster A and B:", single_linkage_max)

Ligação média (média)

Esse critério analisa a distância média entre todos os pontos em um cluster e todos os pontos em outro. Isso proporciona um equilíbrio entre a ligação única e a completa.

average_linkage = np.mean(distance_matrix[0, 1:])
print("Average Linkage Distance between Cluster A and B:", average_linkage)

Esses exemplos simplificados ilustram como as distâncias são inicialmente computadas. No entanto, durante o clustering, esses critérios (ligação única, completa e média) aplicam distâncias iterativamente entre clusters inteiros, não apenas pontos individuais.

Método de Ward

O método de Ward é uma variação da abordagem de ligação média que minimiza a soma das diferenças quadradas em todos os clusters. Ele tende a produzir clusters de tamanho mais uniforme em comparação com outros métodos. Também costuma resultar em grupos esféricos bem separados.

from scipy.cluster.hierarchy import linkage
linkage_ward = linkage(data, method='ward')
print("Ward's Linkage Matrix:\n", linkage_ward)

Cada método tem seus próprios pontos fortes e deve ser escolhido com base nos dados e no caso de uso.

3. Métricas de distância

A métrica de distância usada influencia significativamente o resultado do agrupamento.

Distância euclidiana

A distância distância euclidiana é a distância em linha reta entre dois pontos no espaço multidimensional. É a métrica de distância mais comumente usada, especialmente para dados geometricamente distribuídos.

Distância de Manhattan

A distância de Manhattan, também conhecida como distância de táxi ou L1, é a soma das diferenças absolutas entre as dimensões. É útil para dados em forma de grade, como quadras de cidades ou transações financeiras.

Similaridade de cosseno

Similaridade de cosseno mede o cosseno do ângulo entre dois vetores diferentes de zero. Essa métrica é ideal para dados de texto ou quando a magnitude não importa (por exemplo, vetores de frequência de palavras).

Implementando o agrupamento hierárquico em Python

Nesta seção, apresentaremos uma implementação prática do agrupamento hierárquico aglomerativo usando Python. Cobriremos tudo, desde o pré-processamento de dados até a visualização dos resultados usando um dendrograma.

Bibliotecas

Começamos importando as bibliotecas necessárias:

import numpy as np
import pandas as pd
from scipy.cluster.hierarchy import dendrogram, linkage, fcluster
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt

Aqui está o que importamos no código acima:

• numpy e pandas para manipulação de dados
• scipy.cluster.hierarchy para agrupamento e geração de dendrogramas
• sklearn.preprocessing.StandardScaler para dimensionamento de recursos
• matplotlib para visualização

Dados de amostra

Antes de iniciarmos nossa análise, vamos criar um conjunto de dados de brinquedo de pontos 2D e dimensioná-lo. Você pode usar o conjunto de dados de brinquedo para criar um conjunto de dados de pontos 2D. O dimensionamento é fundamental para os algoritmos baseados em distância.

Esta é a aparência do nosso conjunto de dados de amostra.

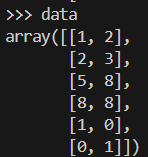
data = np.array([[1, 2], [2, 3], [5, 8], [8, 8], [1, 0], [0, 1]])
scaler = StandardScaler()
data_scaled = scaler.fit_transform(data)

Aqui você vê como fica a matriz de dados depois de ter sido dimensionada.

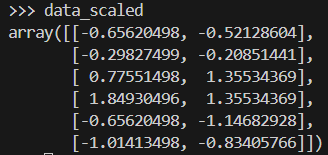
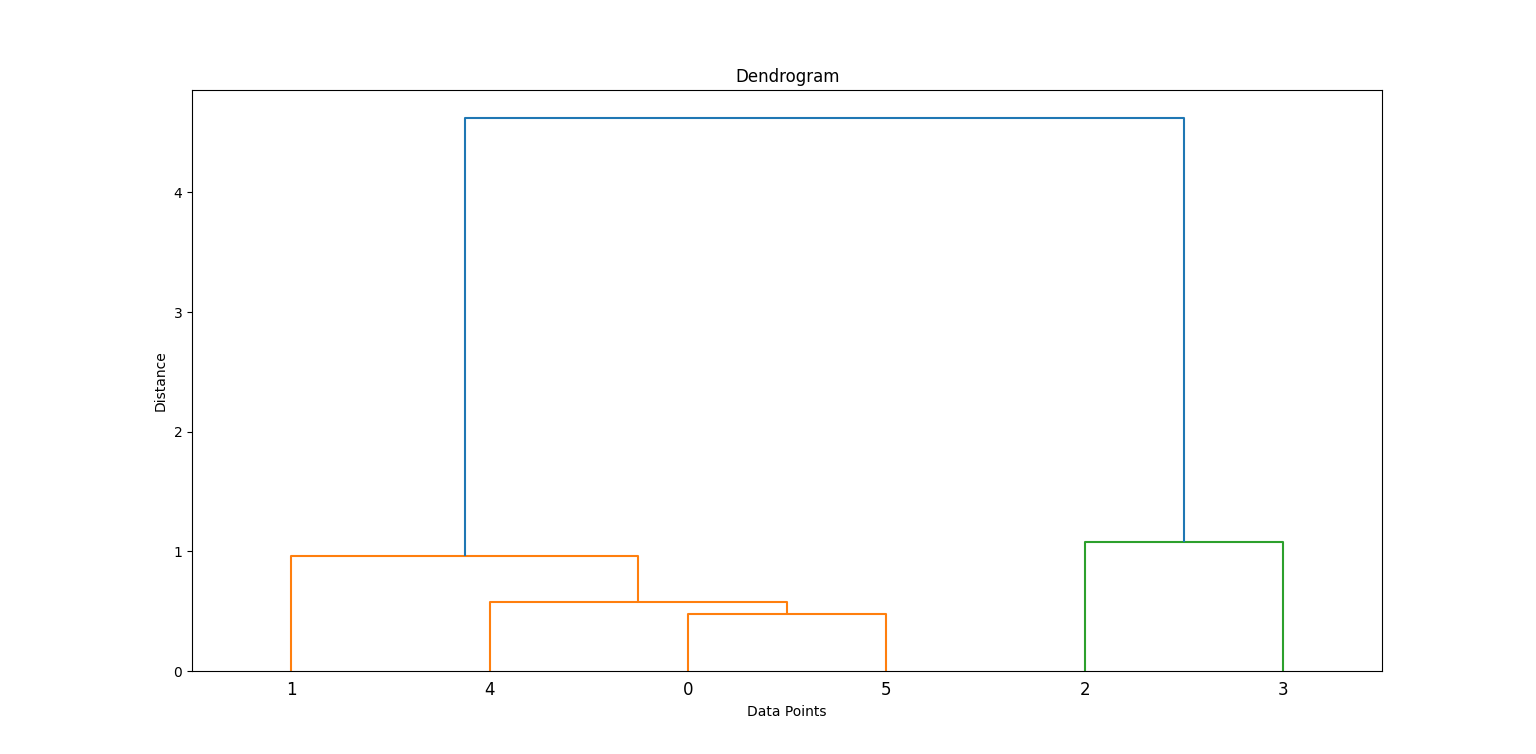
Geração de uma matriz de ligação e dendrograma

Aplicamos o método de Ward para gerar uma matriz de ligação, que contém informações de agrupamento hierárquico. Em seguida, traçamos um dendrograma.

linkage_matrix = linkage(data_scaled, method='ward')
plt.figure(figsize=(8, 4))
dendrogram(linkage_matrix)
plt.title('Dendrogram')
plt.xlabel('Data Points')
plt.ylabel('Distance')
plt.show()

No código acima, linkage cria a hierarquia de clusters e dendrogram ajuda a visualizar como os clusters foram formados.

Ao examinar onde as linhas verticais são mais longas antes de uma mesclagem, podemos decidir onde "cortar" para formar clusters. Procure a linha vertical mais alta que não se cruza com nenhum outro agrupamento. É aqui que você terá que fazer o corte.

Nesse caso, você precisará cortar 2 cachos.

Criação de clusters

Em seguida, cortamos o dendrograma para obter um número específico de clusters usando fcluster:

clusters = fcluster(linkage_matrix, t=2, criterion='maxclust')
print(clusters)

plt.scatter(data_scaled[:, 0], data_scaled[:, 1], c=clusters, cmap='rainbow')
plt.title('Clusters')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.show()

Isso atribui cada ponto de dados a um de dois clusters.

Algumas informações adicionais sobre o código:

• t=2: Especifica o número desejado de clusters.
• criterion='maxclust': Garante que você obtenha exatamente t clusters.

Você pode alterar t para experimentar diferentes números de clusters.

Exemplo prático: Segmentação de clientes

O agrupamento hierárquico é normalmente usado na segmentação de clientes. Vamos ver como isso fica em uma implementação prática.

1. Visão geral do conjunto de dados

Vamos simular um conjunto de dados que representa clientes com dois recursos: idade e renda. Usaremos o site make_blobs para gerar esses dados sintéticos.

from sklearn.datasets import make_blobs
X, _ = make_blobs(n_samples=100, centers=3, n_features=2, random_state=42)

2. Pré-processamento

Em seguida, precisaremos padronizar os recursos para normalizar as escalas e melhorar a precisão do agrupamento.

scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

Aqui está a aparência dos dados em escala:

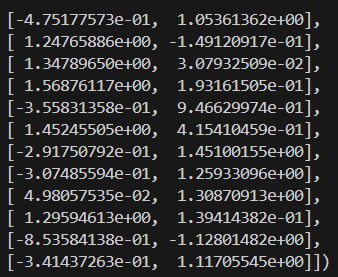
3. Aplicação de agrupamento hierárquico

Agora que nossos dados foram processados, traçaremos o dendrograma para visualizar como os grupos se formam.

linkage_matrix = linkage(X_scaled, method='ward')
plt.figure(figsize=(10, 5))
dendrogram(linkage_matrix)
plt.title('Customer Dendrogram')
plt.xlabel('Sample Index')
plt.ylabel('Distance')
plt.show()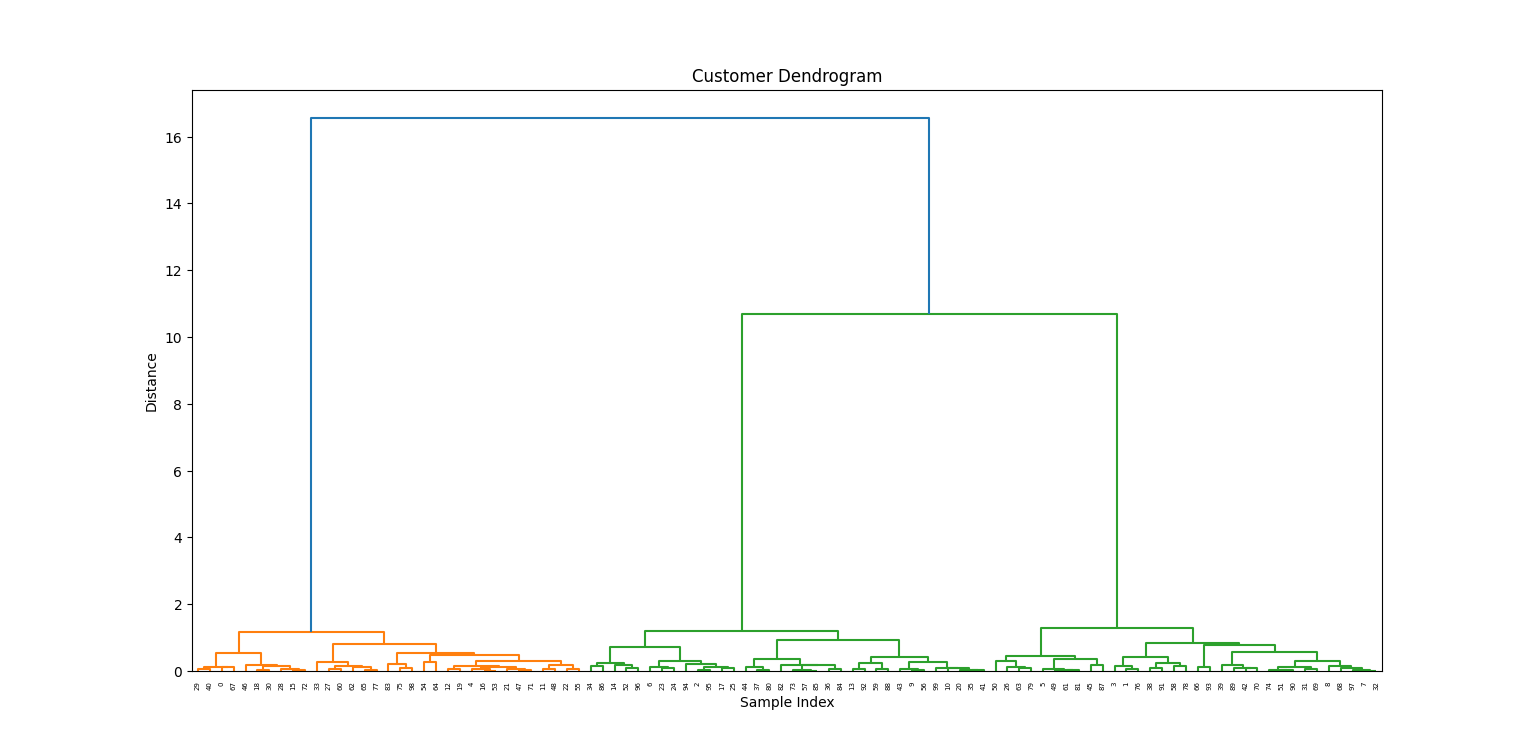

4. Interpretação dos resultados

No dendrograma, escolhemos uma altura para "cortar" e criar três grupos:

labels = fcluster(linkage_matrix, t=3, criterion='maxclust')
plt.scatter(X_scaled[:, 0], X_scaled[:, 1], c=labels, cmap='rainbow')
plt.title('Customer Segments')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.show()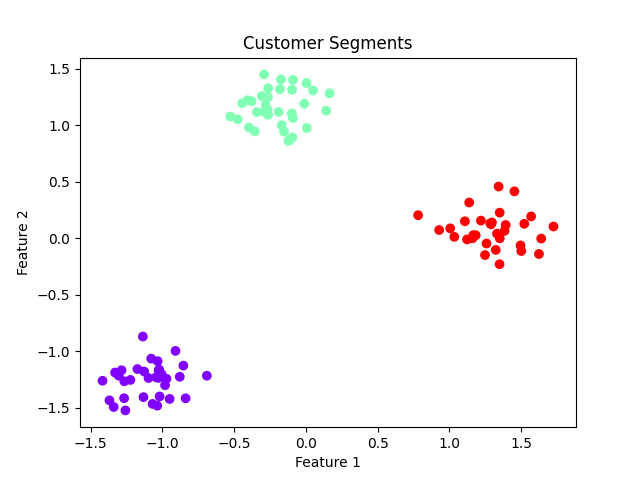

Implicações comerciais:

• Os clusters podem representar grupos de clientes, como clientes preocupados com o orçamento, clientes de nível médio e clientes premium.
• Permite marketing personalizado e estratégias aprimoradas de relacionamento com o cliente.

Vantagens e limitações do clustering hierárquico

A escolha do agrupamento hierárquico para sua análise tem várias vantagens e limitações. 

Veja abaixo algumas das mais comuns:

Prós

• Não há necessidade de especificar o número de clusters: Você pode escolher após a inspeção visual do dendrograma.
• Visualização intuitiva: Os dendrogramas ajudam a entender como os agrupamentos se formam.
• Flexível: Pode lidar com vários formatos de clusters, dependendo das métricas de ligação e distância.

Contras

• Computacionalmente intensivo: Não é ideal para grandes conjuntos de dados.
• Sensível a ruídos e discrepâncias: Alguns valores discrepantes podem distorcer significativamente o dendrograma.
• Não há reatribuição: Depois que uma mesclagem é feita, ela não pode ser desfeita, o que pode levar a um agrupamento abaixo do ideal.

Conclusão

O agrupamento hierárquico é uma técnica de agrupamento versátil e interpretável que é especialmente útil na análise exploratória de dados e em domínios como genômica e segmentação de clientes. Apesar de seu custo computacional, seu ponto forte está na capacidade de descobrir agrupamentos aninhados e na flexibilidade de escolher o número de clusters post-hoc por meio da visualização do dendrograma.

Para conjuntos de dados de pequeno e médio porte, em que a interpretabilidade é fundamental, o clustering hierárquico continua sendo um método de referência para cientistas e analistas de dados.

Você quer saber mais sobre os detalhes do machine learning? Nossos Fundamentos de machine learning em Python e o programa Introdução ao agrupamento hierárquico em Python são ótimos lugares para você começar.